17.1 勾股定理-第2课时 勾股定理的实际应用 分层训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 17.1 勾股定理-第2课时 勾股定理的实际应用 分层训练(含答案)初中数学人教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 115.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:39:48 | ||
图片预览

文档简介
第2课时 勾股定理的实际应用
A组·基础达标 逐点击破
知识点1 勾股定理在实际问题中的应用
1.如图,为了测量小区池塘的最宽处,两点间的距离,在池塘边取一点,使 ,并测得的长为,的长为,则最宽处的距离为( )
第1题图
A. B. C. D.
2.如图,一根木杆斜靠在一建筑物上,此时木杆的底端离建筑物,且木杆的长为,则这根木杆可以达到建筑物的高度是( )
第2题图
A. B. C. D.
3.如图,将一根长为的筷子,置于底面直径为,高为的圆柱形水杯中,设筷子露在杯子外面的长为,则的取值范围是( )
第3题图
A. B.
C. D.
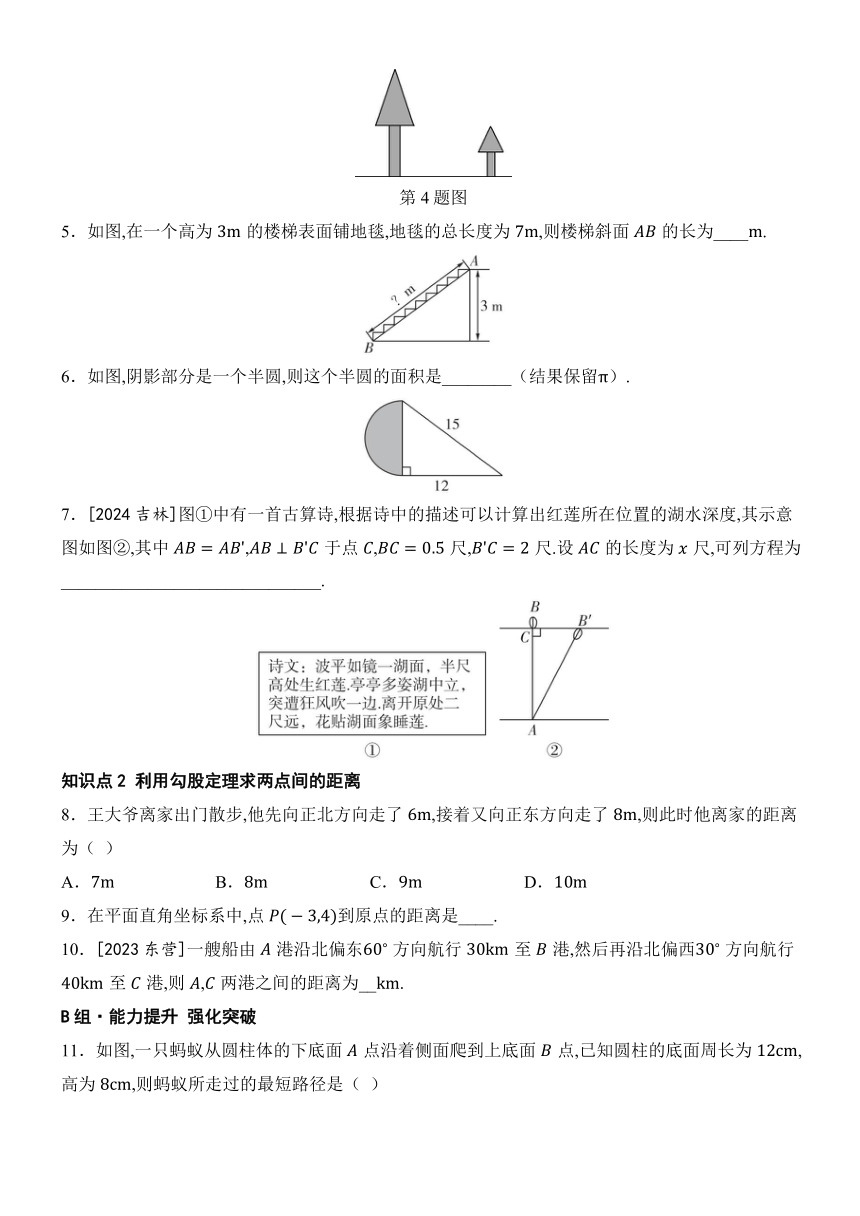
4.如图,有两棵树,一棵高,另一棵高,两树相距.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行了__.
第4题图
5.如图,在一个高为的楼梯表面铺地毯,地毯的总长度为,则楼梯斜面的长为____.
6.如图,阴影部分是一个半圆,则这个半圆的面积是________(结果保留).
7.[2024吉林]图①中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图②,其中,于点,尺,尺.设的长度为尺,可列方程为______________________________.
知识点2 利用勾股定理求两点间的距离
8.王大爷离家出门散步,他先向正北方向走了,接着又向正东方向走了,则此时他离家的距离为( )
A. B. C. D.
9.在平面直角坐标系中,点到原点的距离是____.
10.[2023东营]一艘船由港沿北偏东 方向航行至港,然后再沿北偏西 方向航行至港,则,两港之间的距离为__.
B组·能力提升 强化突破
11.如图,一只蚂蚁从圆柱体的下底面点沿着侧面爬到上底面点,已知圆柱的底面周长为,高为,则蚂蚁所走过的最短路径是( )
A. B. C. D.
12.折竹抵地(源自《九章算术》):“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”大意为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子处3尺远.求竹子折断处离地面的高度.(1丈尺)
13.[2024长沙模拟]如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,求小巷的宽度.
C组·核心素养拓展 素养渗透
14.【应用意识,模型观念】我国明代杰出的数学家程大位在所著的《直指算法统宗》里有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”诗的意思是:当秋千静止时,秋千的踏板离地的距离为一尺,将秋千的踏板往前推两步,这里的每一步合五尺,秋千的踏板与人一样高.这个人的身高为五尺,当然这时秋千的绳索是呈直线状态的,求这个秋千的绳索有多长.
第2课时 勾股定理的实际应用
A组·基础达标 逐点击破
知识点1 勾股定理在实际问题中的应用
1.D 2.A 3.D
4.10
5.5
6.
7.
知识点2 利用勾股定理求两点间的距离
8.D
9.5
10.50
B组·能力提升 强化突破
11.C
12.解:设竹子折断处离地面的高度为尺,则斜边为尺,
根据勾股定理,得,
解得.
答:竹子折断处离地面的高度为4.55尺.
13.解:在中, ,,,
根据勾股定理,得.
在中, ,,
根据勾股定理,得,
.
,
.
.
答:小巷的宽度为.
C组·核心素养拓展 素养渗透
14.解:设秋千的绳索长为尺.
根据题意,得,
解得.
答:秋千的绳索长14.5尺.
A组·基础达标 逐点击破
知识点1 勾股定理在实际问题中的应用
1.如图,为了测量小区池塘的最宽处,两点间的距离,在池塘边取一点,使 ,并测得的长为,的长为,则最宽处的距离为( )
第1题图
A. B. C. D.
2.如图,一根木杆斜靠在一建筑物上,此时木杆的底端离建筑物,且木杆的长为,则这根木杆可以达到建筑物的高度是( )
第2题图
A. B. C. D.
3.如图,将一根长为的筷子,置于底面直径为,高为的圆柱形水杯中,设筷子露在杯子外面的长为,则的取值范围是( )
第3题图
A. B.
C. D.
4.如图,有两棵树,一棵高,另一棵高,两树相距.一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行了__.
第4题图
5.如图,在一个高为的楼梯表面铺地毯,地毯的总长度为,则楼梯斜面的长为____.
6.如图,阴影部分是一个半圆,则这个半圆的面积是________(结果保留).
7.[2024吉林]图①中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图②,其中,于点,尺,尺.设的长度为尺,可列方程为______________________________.
知识点2 利用勾股定理求两点间的距离
8.王大爷离家出门散步,他先向正北方向走了,接着又向正东方向走了,则此时他离家的距离为( )
A. B. C. D.
9.在平面直角坐标系中,点到原点的距离是____.
10.[2023东营]一艘船由港沿北偏东 方向航行至港,然后再沿北偏西 方向航行至港,则,两港之间的距离为__.
B组·能力提升 强化突破
11.如图,一只蚂蚁从圆柱体的下底面点沿着侧面爬到上底面点,已知圆柱的底面周长为,高为,则蚂蚁所走过的最短路径是( )
A. B. C. D.
12.折竹抵地(源自《九章算术》):“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”大意为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子处3尺远.求竹子折断处离地面的高度.(1丈尺)
13.[2024长沙模拟]如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,求小巷的宽度.
C组·核心素养拓展 素养渗透
14.【应用意识,模型观念】我国明代杰出的数学家程大位在所著的《直指算法统宗》里有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地,送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉,良工高士素好奇,算出索长有几?”诗的意思是:当秋千静止时,秋千的踏板离地的距离为一尺,将秋千的踏板往前推两步,这里的每一步合五尺,秋千的踏板与人一样高.这个人的身高为五尺,当然这时秋千的绳索是呈直线状态的,求这个秋千的绳索有多长.
第2课时 勾股定理的实际应用
A组·基础达标 逐点击破
知识点1 勾股定理在实际问题中的应用
1.D 2.A 3.D
4.10
5.5
6.
7.
知识点2 利用勾股定理求两点间的距离
8.D
9.5
10.50
B组·能力提升 强化突破
11.C
12.解:设竹子折断处离地面的高度为尺,则斜边为尺,
根据勾股定理,得,
解得.
答:竹子折断处离地面的高度为4.55尺.
13.解:在中, ,,,
根据勾股定理,得.
在中, ,,
根据勾股定理,得,
.
,
.
.
答:小巷的宽度为.
C组·核心素养拓展 素养渗透
14.解:设秋千的绳索长为尺.
根据题意,得,
解得.
答:秋千的绳索长14.5尺.
