17.1 勾股定理 第3课时 利用勾股定理证明与作图 分层训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 17.1 勾股定理 第3课时 利用勾股定理证明与作图 分层训练(含答案)初中数学人教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 154.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 00:00:00 | ||
图片预览

文档简介
第3课时 利用勾股定理证明与作图
A组·基础达标 逐点击破
知识点1 用勾股定理证明“”定理
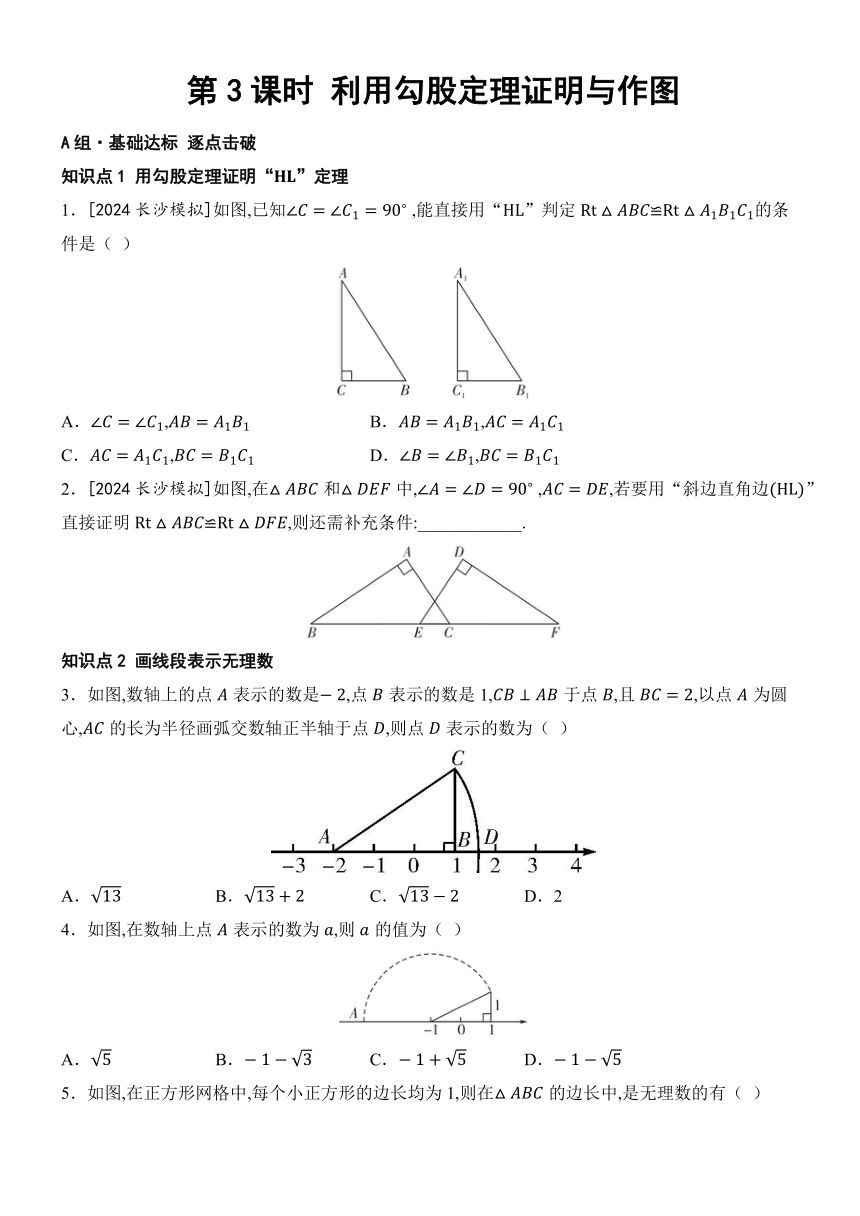
1.[2024长沙模拟]如图,已知 ,能直接用“”判定的条件是( )
A., B.,
C., D.,
2.[2024长沙模拟]如图,在和中, ,,若要用“斜边直角边”直接证明,则还需补充条件:____________.
知识点2 画线段表示无理数
3.如图,数轴上的点表示的数是,点表示的数是1,于点,且,以点为圆心,的长为半径画弧交数轴正半轴于点,则点表示的数为( )
A. B. C. D.2
4.如图,在数轴上点表示的数为,则的值为( )
A. B. C. D.
5.如图,在正方形网格中,每个小正方形的边长均为1,则在的边长中,是无理数的有( )
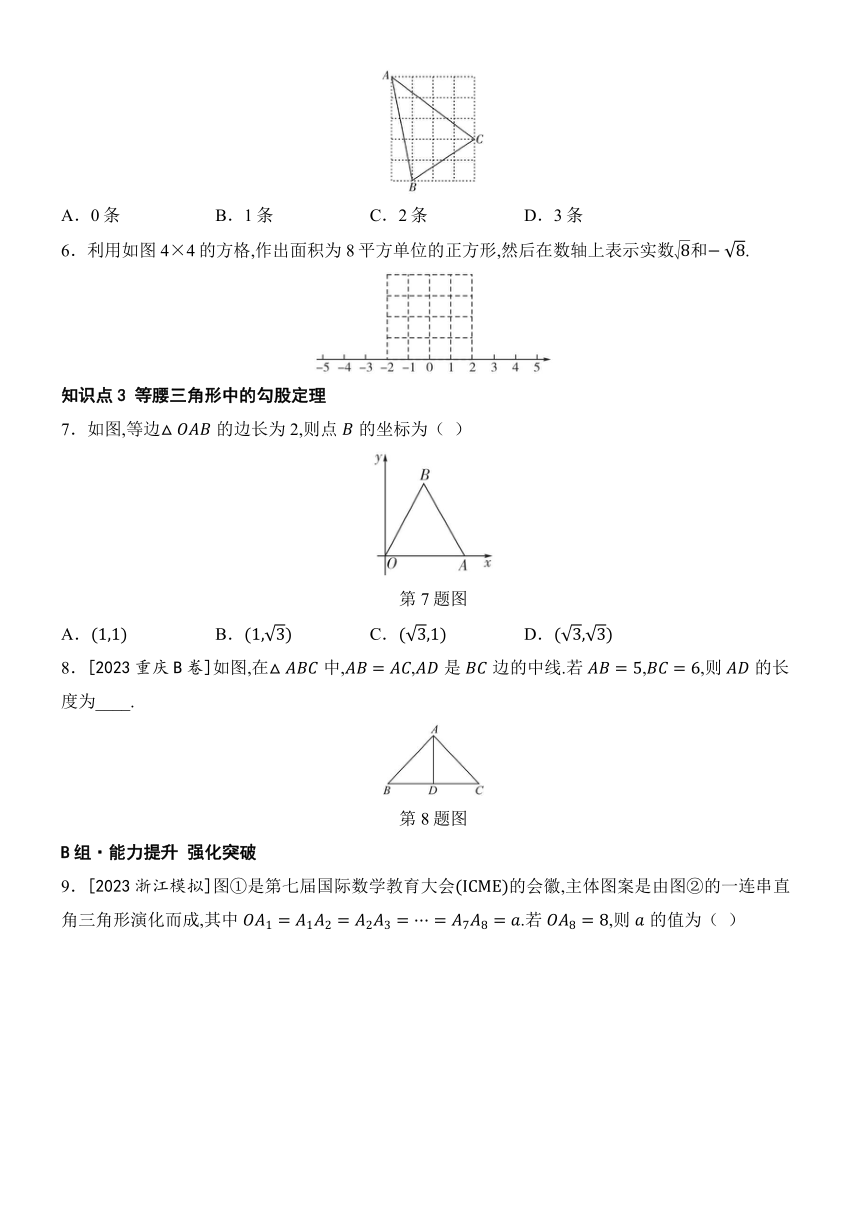
A.0条 B.1条 C.2条 D.3条
6.利用如图4×4的方格,作出面积为8平方单位的正方形,然后在数轴上表示实数和.
知识点3 等腰三角形中的勾股定理
7.如图,等边的边长为2,则点的坐标为( )
第7题图
A. B. C. D.
8.[2023重庆B卷]如图,在中,,是边的中线.若,,则的长度为____.
第8题图
B组·能力提升 强化突破
9.[2023浙江模拟]图①是第七届国际数学教育大会的会徽,主体图案是由图②的一连串直角三角形演化而成,其中.若,则的值为( )
A. B.2 C. D.1
10.[2024安徽]如图,在中, ,,点在的延长线上,且,则的长是( )
A. B. C. D.
11.如图,牧童在处放牛,其家在处,,到河岸的距离分别为,,已知,,且.
(1) 牧童从处放牛牵到河边饮水后再回家,试问:在何处饮水,所走路程最短?
(2) 最短路程是多少?
C组·核心素养拓展 素养渗透
12.【推理能力】(教材P29习题变式)如图,和都是等腰直角三角形,,,的顶点在的斜边上,连接.
(1) 试判断与是否全等,请说明理由;
(2) 求的度数;
(3) 求证:
第3课时 利用勾股定理证明与作图
A组·基础达标 逐点击破
知识点1 用勾股定理证明“”定理
1.B
2.
知识点2 画线段表示无理数
3.C
4.D
[解析]如答图,,
第4题答图
,
.
故选D.
5.C
6.解:如答图.
第6题答图
知识点3 等腰三角形中的勾股定理
7.B
8.4
B组·能力提升 强化突破
9.A 10.B
11.(1) 解:如答图,作点关于直线的对称点,连接交于点,则在点处饮水,所走路程最短.
第11题答图
(2) 如答图,过点作交的延长线于点.
由题意,得,.
由勾股定理,得
.
最短路程为.
C组·核心素养拓展 素养渗透
12.(1) 解:.理由如下:
,
.
在和中,
.
(2) 解: ,,
.
,
.
(3) 证明:是等腰直角三角形,
, ,
.
,,
A组·基础达标 逐点击破
知识点1 用勾股定理证明“”定理
1.[2024长沙模拟]如图,已知 ,能直接用“”判定的条件是( )
A., B.,
C., D.,
2.[2024长沙模拟]如图,在和中, ,,若要用“斜边直角边”直接证明,则还需补充条件:____________.
知识点2 画线段表示无理数
3.如图,数轴上的点表示的数是,点表示的数是1,于点,且,以点为圆心,的长为半径画弧交数轴正半轴于点,则点表示的数为( )
A. B. C. D.2
4.如图,在数轴上点表示的数为,则的值为( )
A. B. C. D.
5.如图,在正方形网格中,每个小正方形的边长均为1,则在的边长中,是无理数的有( )
A.0条 B.1条 C.2条 D.3条
6.利用如图4×4的方格,作出面积为8平方单位的正方形,然后在数轴上表示实数和.
知识点3 等腰三角形中的勾股定理
7.如图,等边的边长为2,则点的坐标为( )
第7题图
A. B. C. D.
8.[2023重庆B卷]如图,在中,,是边的中线.若,,则的长度为____.
第8题图
B组·能力提升 强化突破
9.[2023浙江模拟]图①是第七届国际数学教育大会的会徽,主体图案是由图②的一连串直角三角形演化而成,其中.若,则的值为( )
A. B.2 C. D.1
10.[2024安徽]如图,在中, ,,点在的延长线上,且,则的长是( )
A. B. C. D.
11.如图,牧童在处放牛,其家在处,,到河岸的距离分别为,,已知,,且.
(1) 牧童从处放牛牵到河边饮水后再回家,试问:在何处饮水,所走路程最短?
(2) 最短路程是多少?
C组·核心素养拓展 素养渗透
12.【推理能力】(教材P29习题变式)如图,和都是等腰直角三角形,,,的顶点在的斜边上,连接.
(1) 试判断与是否全等,请说明理由;
(2) 求的度数;
(3) 求证:
第3课时 利用勾股定理证明与作图
A组·基础达标 逐点击破
知识点1 用勾股定理证明“”定理
1.B
2.
知识点2 画线段表示无理数
3.C
4.D
[解析]如答图,,
第4题答图
,
.
故选D.
5.C
6.解:如答图.
第6题答图
知识点3 等腰三角形中的勾股定理
7.B
8.4
B组·能力提升 强化突破
9.A 10.B
11.(1) 解:如答图,作点关于直线的对称点,连接交于点,则在点处饮水,所走路程最短.
第11题答图
(2) 如答图,过点作交的延长线于点.
由题意,得,.
由勾股定理,得
.
最短路程为.
C组·核心素养拓展 素养渗透
12.(1) 解:.理由如下:
,
.
在和中,
.
(2) 解: ,,
.
,
.
(3) 证明:是等腰直角三角形,
, ,
.
,,
