18.1.2 平行四边形的判定 分层训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 18.1.2 平行四边形的判定 分层训练(含答案)初中数学人教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 203.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:41:47 | ||
图片预览



文档简介
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
A组·基础达标 逐点击破
知识点1 两组对边分别平行的四边形是平行四边形
1.在四边形中,,要判定四边形是平行四边形,则还需满足( )
A. B.
C. D.
知识点2 两组对边分别相等的四边形是平行四边形
2.[2023 河北模拟]要使如图所示的四边形是平行四边形,根据图中数据,可以添加的条件是( )
第2题图
A. B. C. D.
知识点3 两组对角分别相等的四边形是平行四边形
3.如图,在四边形中,,则下列条件不能判定四边形为平行四边形的是( )
第3题图
A. B.
C. D.
4.小敏不慎将一块平行四边形的玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①② B.①④ C.③④ D.②③
知识点4 对角线互相平分的四边形是平行四边形
5.四边形的对角线与相交于点,下列四组条件中,一定能判定四边形为平行四边形的是( )
A. B.,
C., D.
知识点5 一组对边平行且相等的四边形是平行四边形
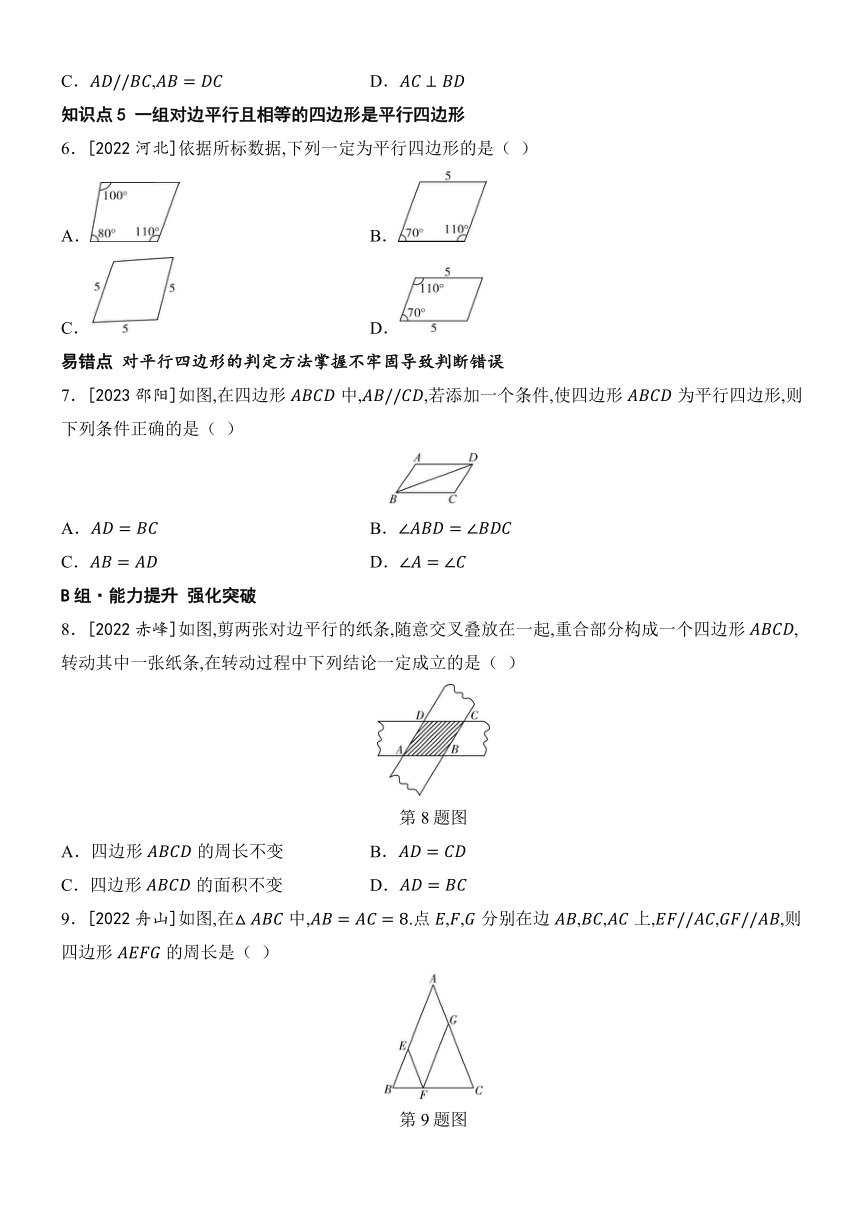
6.[2022河北]依据所标数据,下列一定为平行四边形的是( )
A. B.
C. D.
易错点 对平行四边形的判定方法掌握不牢固导致判断错误
7.[2023邵阳]如图,在四边形中,,若添加一个条件,使四边形为平行四边形,则下列条件正确的是( )
A. B.
C. D.
B组·能力提升 强化突破
8.[2022赤峰]如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形,转动其中一张纸条,在转动过程中下列结论一定成立的是( )
第8题图
A.四边形的周长不变 B.
C.四边形的面积不变 D.
9.[2022舟山]如图,在中,.点,,分别在边,,上,,,则四边形的周长是( )
第9题图
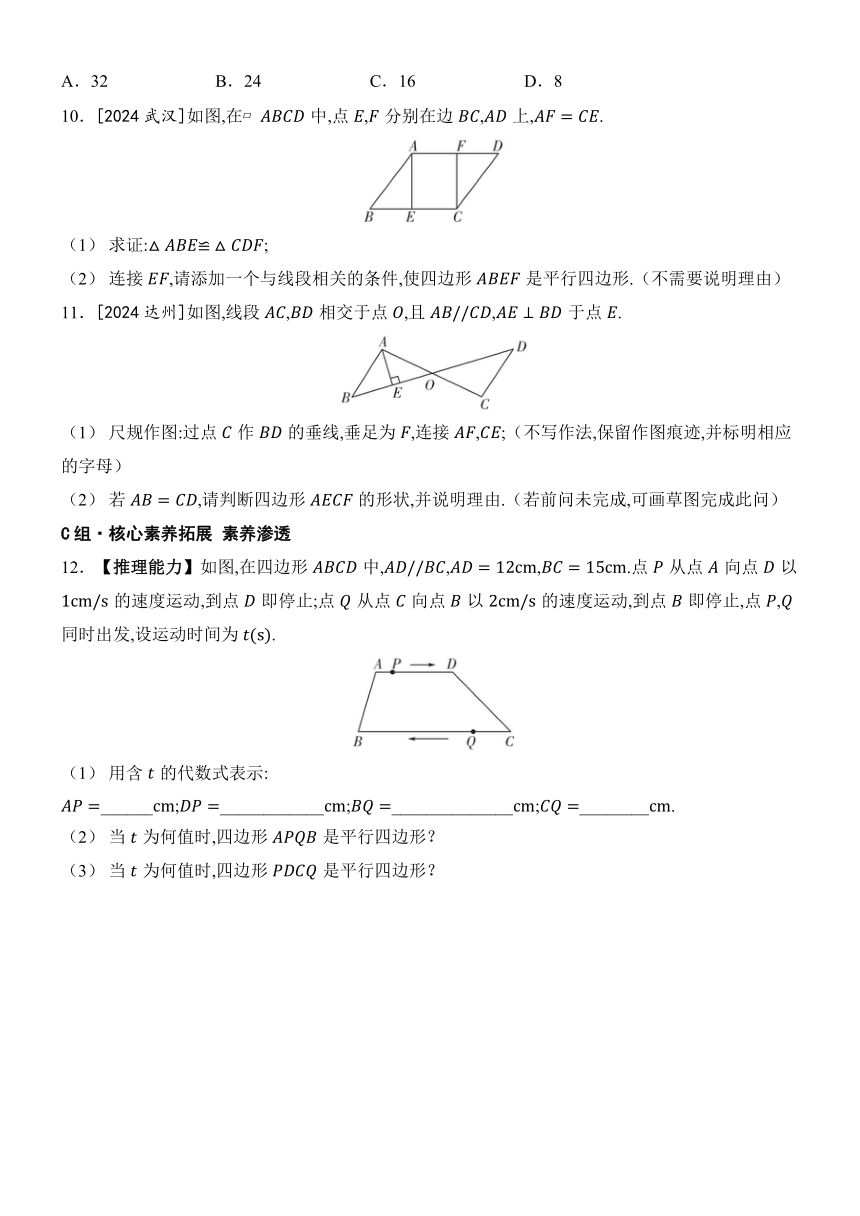
A.32 B.24 C.16 D.8
10.[2024武汉]如图,在中,点,分别在边,上,.
(1) 求证:;
(2) 连接,请添加一个与线段相关的条件,使四边形是平行四边形.(不需要说明理由)
11.[2024达州]如图,线段,相交于点,且,于点.
(1) 尺规作图:过点作的垂线,垂足为,连接,;(不写作法,保留作图痕迹,并标明相应的字母)
(2) 若,请判断四边形的形状,并说明理由.(若前问未完成,可画草图完成此问)
C组·核心素养拓展 素养渗透
12.【推理能力】如图,在四边形中,,,.点从点向点以的速度运动,到点即停止;点从点向点以的速度运动,到点即停止,点,同时出发,设运动时间为.
(1) 用含的代数式表示:
______;____________;______________;________.
(2) 当为何值时,四边形是平行四边形?
(3) 当为何值时,四边形是平行四边形?
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
A组·基础达标 逐点击破
知识点1 两组对边分别平行的四边形是平行四边形
1.A
知识点2 两组对边分别相等的四边形是平行四边形
2.C
知识点3 两组对角分别相等的四边形是平行四边形
3.D 4.D
知识点4 对角线互相平分的四边形是平行四边形
5.B
知识点5 一组对边平行且相等的四边形是平行四边形
6.D
易错点 对平行四边形的判定方法掌握不牢固导致判断错误
7.D
B组·能力提升 强化突破
8.D 9.C
10.(1) 证明: 四边形是平行四边形,
,,.
,
,.
在和中,
.
(2) 解:添加.
11.(1) 解:如答图,,,为所作.
第11题答图
(2) 四边形是平行四边形.理由如下:
,.
,,
, .
在和中,
,.
,
四边形是平行四边形.
C组·核心素养拓展 素养渗透
12.(1) ; ; ;
(2) 解:,
当时,四边形是平行四边形.
,,
,解得.
当时,四边形是平行四边形.
(3) ,即,
当时,四边形是平行四边形.
,,
,
解得,
当时,四边形是平行四边形.
第2课时 三角形的中位线
A组·基础达标 逐点击破
知识点1 三角形的中位线的证明
1.[2023河北模拟]数学课上,大家一起研究三角形中位线定理的证明.嘉嘉和淇淇各自尝试作了一种辅助线,如图①,②.其中辅助线作法能够用来证明三角形中位线定理的是( )
A.嘉嘉的作法不可以,淇淇的作法可以
B.嘉嘉的作法可以,淇淇的作法不可以
C.嘉嘉和淇淇的作法都不可以
D.嘉嘉和淇淇的作法都可以
知识点2 三角形的中位线的运用
2.[2024广安]如图,在中,,分别是,的中点,若 , ,则的度数为( )
第2题图
A. B. C. D.
3.(教材P49练习T1变式)以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
4.[2024长沙]如图,在中,,分别是,的中点,连接.若,则的长为__.
第4题图
5.[2024无锡]在中,,,,,,分别是,,的中点,则的周长为____.
6.如图,在中,,,垂足为,是的中点.若,则的长为__.
第6题图
7.如图,的对角线,相交于点,,分别是线段,的中点.若,的周长是,则____.
第7题图
8.如图,在中, , ,,,分别为边,的中点.
(1) 求的度数;
(2) 求的长.
B组·能力提升 强化突破
9.[2023泸州]如图,的对角线,相交于点,的平分线与边相交于点,是的中点.若,,则的长为( )
A.1 B.2 C.3 D.4
10.[2023株洲]如图,在中,,分别为,的中点,点在线段上,连接,,分别为,的中点,连接.
(1) 求证:四边形为平行四边形;
(2) 若,,,求线段的长度.
11.(教材P62习题变式)如图,的中线,相交于点,已知,分别是,的中点.
(1) 求证:四边形是平行四边形;
(2) 请判断与的数量关系,并证明.
C组·核心素养拓展 素养渗透
12.[2023北京模拟]【几何直观,推理能力】如图,在四边形中,已知,,分别为,的中点,延长,,分别交射线于点,.求证:.
第2课时 三角形的中位线
A组·基础达标 逐点击破
知识点1 三角形的中位线的证明
1.D
知识点2 三角形的中位线的运用
2.D 3.C
4.24
5.9
6.10
7.3
8.(1) 解:在中, , ,
.
(2) 在中, , ,,
.
,分别为边,的中点,
是的中位线,
.
B组·能力提升 强化突破
9.A
10.(1) 证明:,分别为,的中点,,分别为,的中点.
是的中位线,是的中位线.
,,,,,,
四边形为平行四边形.
(2) 解:四边形为平行四边形,
.
, .
.
11.(1) 证明:,是的中线,
是的中位线,
,.
,分别是,的中点,
是的中位线,
,.
,,
四边形是平行四边形.
(2) 解:.证明如下:
四边形是平行四边形,
.
是的中点,
,.
C组·核心素养拓展 素养渗透
12.证明:如答图,连接,取的中点,连接,.
第12题答图
是的中点,是的中点,
是的中位线,
,,
.
同理可证,,,
.
又,
,
,
.
第1课时 平行四边形的判定
A组·基础达标 逐点击破
知识点1 两组对边分别平行的四边形是平行四边形
1.在四边形中,,要判定四边形是平行四边形,则还需满足( )
A. B.
C. D.
知识点2 两组对边分别相等的四边形是平行四边形
2.[2023 河北模拟]要使如图所示的四边形是平行四边形,根据图中数据,可以添加的条件是( )
第2题图
A. B. C. D.
知识点3 两组对角分别相等的四边形是平行四边形
3.如图,在四边形中,,则下列条件不能判定四边形为平行四边形的是( )
第3题图
A. B.
C. D.
4.小敏不慎将一块平行四边形的玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①② B.①④ C.③④ D.②③
知识点4 对角线互相平分的四边形是平行四边形
5.四边形的对角线与相交于点,下列四组条件中,一定能判定四边形为平行四边形的是( )
A. B.,
C., D.
知识点5 一组对边平行且相等的四边形是平行四边形
6.[2022河北]依据所标数据,下列一定为平行四边形的是( )
A. B.
C. D.
易错点 对平行四边形的判定方法掌握不牢固导致判断错误
7.[2023邵阳]如图,在四边形中,,若添加一个条件,使四边形为平行四边形,则下列条件正确的是( )
A. B.
C. D.
B组·能力提升 强化突破
8.[2022赤峰]如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形,转动其中一张纸条,在转动过程中下列结论一定成立的是( )
第8题图
A.四边形的周长不变 B.
C.四边形的面积不变 D.
9.[2022舟山]如图,在中,.点,,分别在边,,上,,,则四边形的周长是( )
第9题图
A.32 B.24 C.16 D.8
10.[2024武汉]如图,在中,点,分别在边,上,.
(1) 求证:;
(2) 连接,请添加一个与线段相关的条件,使四边形是平行四边形.(不需要说明理由)
11.[2024达州]如图,线段,相交于点,且,于点.
(1) 尺规作图:过点作的垂线,垂足为,连接,;(不写作法,保留作图痕迹,并标明相应的字母)
(2) 若,请判断四边形的形状,并说明理由.(若前问未完成,可画草图完成此问)
C组·核心素养拓展 素养渗透
12.【推理能力】如图,在四边形中,,,.点从点向点以的速度运动,到点即停止;点从点向点以的速度运动,到点即停止,点,同时出发,设运动时间为.
(1) 用含的代数式表示:
______;____________;______________;________.
(2) 当为何值时,四边形是平行四边形?
(3) 当为何值时,四边形是平行四边形?
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
A组·基础达标 逐点击破
知识点1 两组对边分别平行的四边形是平行四边形
1.A
知识点2 两组对边分别相等的四边形是平行四边形
2.C
知识点3 两组对角分别相等的四边形是平行四边形
3.D 4.D
知识点4 对角线互相平分的四边形是平行四边形
5.B
知识点5 一组对边平行且相等的四边形是平行四边形
6.D
易错点 对平行四边形的判定方法掌握不牢固导致判断错误
7.D
B组·能力提升 强化突破
8.D 9.C
10.(1) 证明: 四边形是平行四边形,
,,.
,
,.
在和中,
.
(2) 解:添加.
11.(1) 解:如答图,,,为所作.
第11题答图
(2) 四边形是平行四边形.理由如下:
,.
,,
, .
在和中,
,.
,
四边形是平行四边形.
C组·核心素养拓展 素养渗透
12.(1) ; ; ;
(2) 解:,
当时,四边形是平行四边形.
,,
,解得.
当时,四边形是平行四边形.
(3) ,即,
当时,四边形是平行四边形.
,,
,
解得,
当时,四边形是平行四边形.
第2课时 三角形的中位线
A组·基础达标 逐点击破
知识点1 三角形的中位线的证明
1.[2023河北模拟]数学课上,大家一起研究三角形中位线定理的证明.嘉嘉和淇淇各自尝试作了一种辅助线,如图①,②.其中辅助线作法能够用来证明三角形中位线定理的是( )
A.嘉嘉的作法不可以,淇淇的作法可以
B.嘉嘉的作法可以,淇淇的作法不可以
C.嘉嘉和淇淇的作法都不可以
D.嘉嘉和淇淇的作法都可以
知识点2 三角形的中位线的运用
2.[2024广安]如图,在中,,分别是,的中点,若 , ,则的度数为( )
第2题图
A. B. C. D.
3.(教材P49练习T1变式)以三角形的三个顶点及三边中点为顶点的平行四边形共有( )
A.1个 B.2个 C.3个 D.4个
4.[2024长沙]如图,在中,,分别是,的中点,连接.若,则的长为__.
第4题图
5.[2024无锡]在中,,,,,,分别是,,的中点,则的周长为____.
6.如图,在中,,,垂足为,是的中点.若,则的长为__.
第6题图
7.如图,的对角线,相交于点,,分别是线段,的中点.若,的周长是,则____.
第7题图
8.如图,在中, , ,,,分别为边,的中点.
(1) 求的度数;
(2) 求的长.
B组·能力提升 强化突破
9.[2023泸州]如图,的对角线,相交于点,的平分线与边相交于点,是的中点.若,,则的长为( )
A.1 B.2 C.3 D.4
10.[2023株洲]如图,在中,,分别为,的中点,点在线段上,连接,,分别为,的中点,连接.
(1) 求证:四边形为平行四边形;
(2) 若,,,求线段的长度.
11.(教材P62习题变式)如图,的中线,相交于点,已知,分别是,的中点.
(1) 求证:四边形是平行四边形;
(2) 请判断与的数量关系,并证明.
C组·核心素养拓展 素养渗透
12.[2023北京模拟]【几何直观,推理能力】如图,在四边形中,已知,,分别为,的中点,延长,,分别交射线于点,.求证:.
第2课时 三角形的中位线
A组·基础达标 逐点击破
知识点1 三角形的中位线的证明
1.D
知识点2 三角形的中位线的运用
2.D 3.C
4.24
5.9
6.10
7.3
8.(1) 解:在中, , ,
.
(2) 在中, , ,,
.
,分别为边,的中点,
是的中位线,
.
B组·能力提升 强化突破
9.A
10.(1) 证明:,分别为,的中点,,分别为,的中点.
是的中位线,是的中位线.
,,,,,,
四边形为平行四边形.
(2) 解:四边形为平行四边形,
.
, .
.
11.(1) 证明:,是的中线,
是的中位线,
,.
,分别是,的中点,
是的中位线,
,.
,,
四边形是平行四边形.
(2) 解:.证明如下:
四边形是平行四边形,
.
是的中点,
,.
C组·核心素养拓展 素养渗透
12.证明:如答图,连接,取的中点,连接,.
第12题答图
是的中点,是的中点,
是的中位线,
,,
.
同理可证,,,
.
又,
,
,
.
