18.1.2 平行四边形的判定 知识点分类训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 18.1.2 平行四边形的判定 知识点分类训练(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 172.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:51:06 | ||
图片预览


文档简介
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
课堂探究 例题点拨
知识点1 两组对边分别平行的四边形是平行四边形
例1 如图,,分别是的边,上的点,且.
求证:.
知识点2 两组对边分别相等的四边形是平行四边形
例2 证明:两组对边分别相等的四边形是平行四边形.
已知:在四边形中,,.
求证:四边形是平行四边形.
【变式】 在四边形中,,.若 ,则的度数为( )
A. B. C. D.
知识点3 两组对角分别相等的四边形是平行四边形
例3 证明:两组对角分别相等的四边形是平行四边形.
已知:如图,在四边形中,,.
求证:四边形是平行四边形.
知识点 对角线互相平分的四边形是平行四边形
例4 证明:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形中,,.
求证:四边形是平行四边形.
【变式】 如图,在中,对角线,相交于点,,,为直线上的两个动点(点,始终在的外部),连接,,,,,.
(1) 求证:四边形是平行四边形;
(2) 若平分, ,求四边形的周长.
知识点5 一组对边平行且相等的四边形是平行四边形
例5 证明:一组对边平行且相等的四边形是平行四边形.
已知:如图,在四边形中,,.
求证:四边形是平行四边形.
例6 (教材P47例4变式)如图,在中,如果,分别是边,的中点,交于点,交于点.
(1) 求证:四边形是平行四边形,四边形是平行四边形.
(2) 求证:四边形是平行四边形.
(3) 若将“,分别是,的中点”改为“点,分别在,上,且”,四边形是否仍为平行四边形?若是平行四边形,请说明理由;若不是平行四边形,请画图举反例说明.
课堂检测 习题巩固
1.如图,,要使四边形成为平行四边形,还需要添加的条件是( )
第1题图
A. B. C. D.
2.下面给出的是四边形中,,,的度数比,其中能判断四边形是平行四边形的是( )
A. B. C. D.
3.如图,四边形的对角线相交于点,,请添加一个条件:____________________________(只添一个即可),使四边形是平行四边形.
第3题图
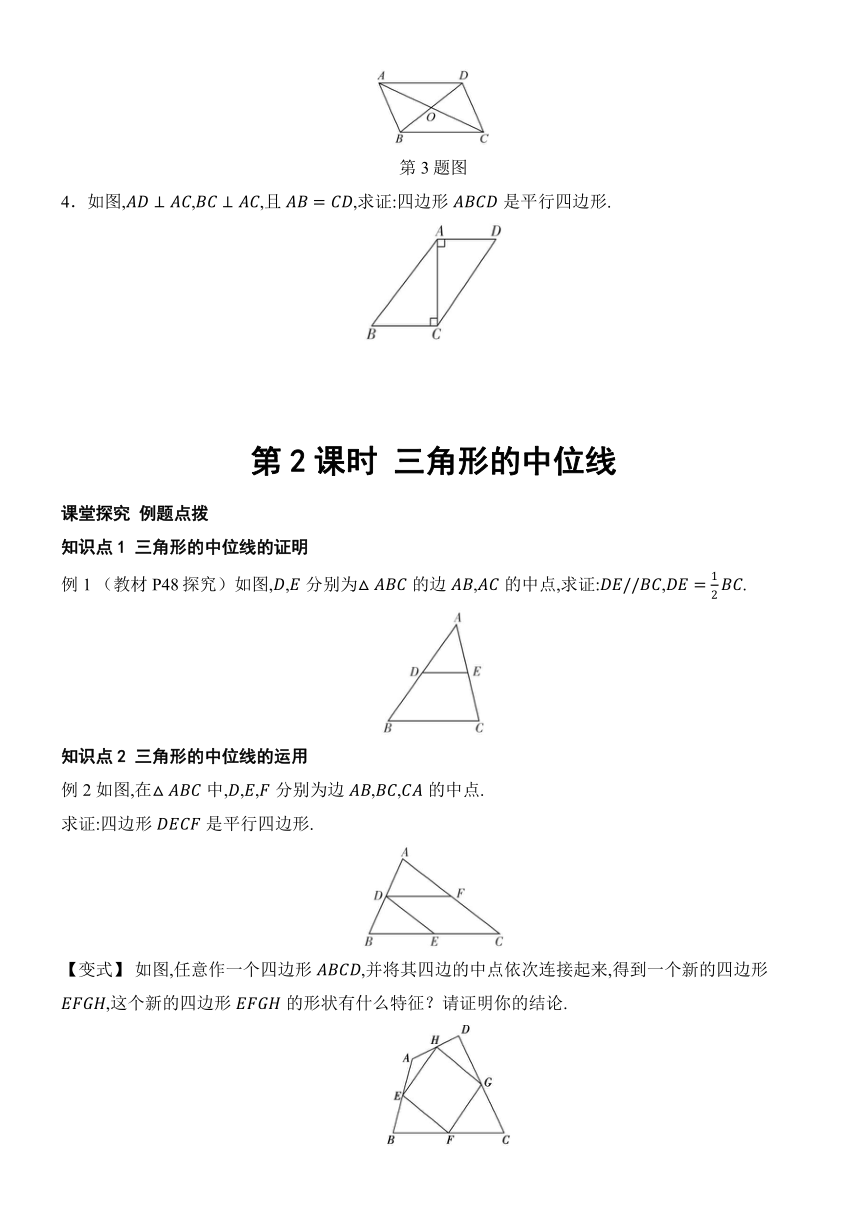
4.如图,,,且,求证:四边形是平行四边形.
第2课时 三角形的中位线
课堂探究 例题点拨
知识点1 三角形的中位线的证明
例1 (教材P48探究)如图,,分别为的边,的中点,求证:,.
知识点2 三角形的中位线的运用
例2 如图,在中,,,分别为边,,的中点.
求证:四边形是平行四边形.
【变式】 如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新的四边形的形状有什么特征?请证明你的结论.
课堂检测 习题巩固
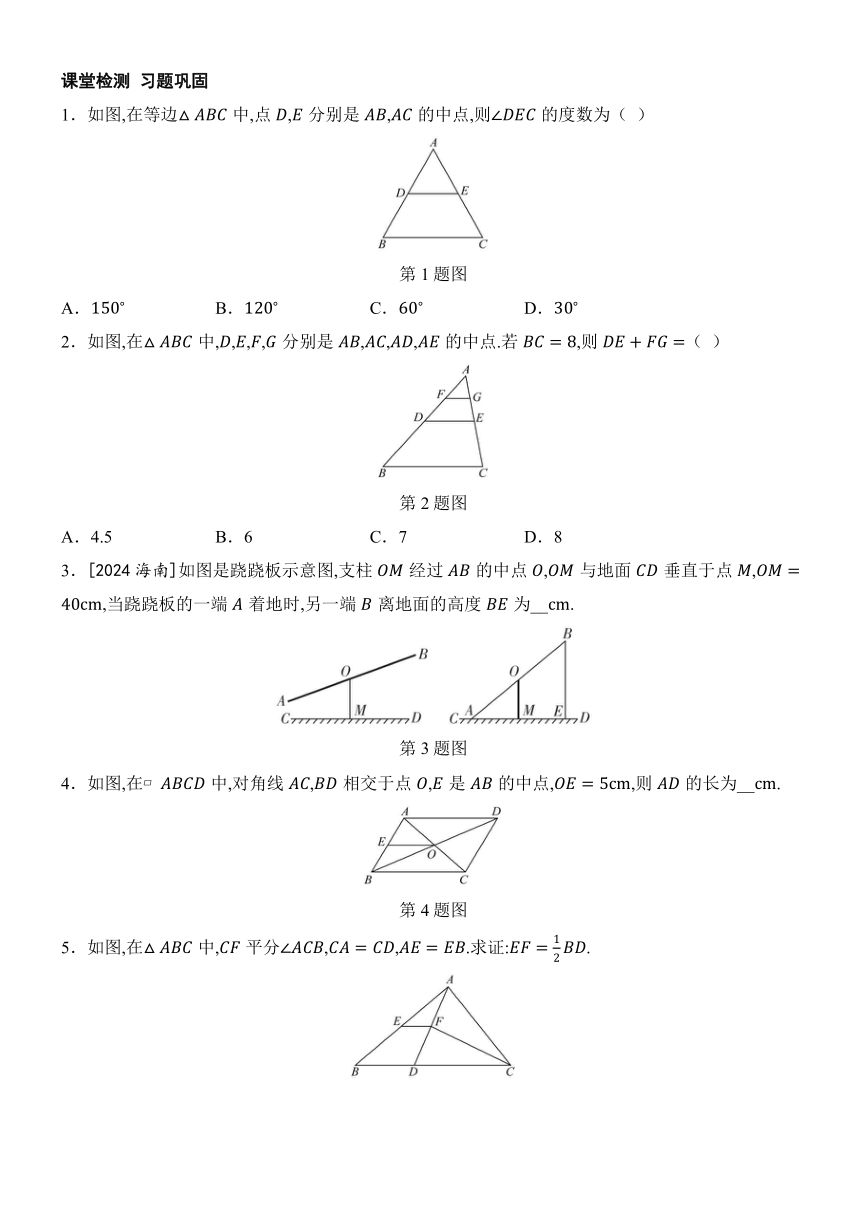
1.如图,在等边中,点,分别是,的中点,则的度数为( )
第1题图
A. B. C. D.
2.如图,在中,,,,分别是,,,的中点.若,则( )
第2题图
A.4.5 B.6 C.7 D.8
3.[2024海南]如图是跷跷板示意图,支柱经过的中点,与地面垂直于点,,当跷跷板的一端着地时,另一端离地面的高度为__.
第3题图
4.如图,在中,对角线,相交于点,是的中点,,则的长为__.
第4题图
5.如图,在中,平分,,.求证:.
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
课堂探究 例题点拨
知识点1 两组对边分别平行的四边形是平行四边形
例1 证明: 四边形是平行四边形,
,.
,,.
, 四边形是平行四边形,.
知识点2 两组对边分别相等的四边形是平行四边形
例2 证明:如答图,连接.
例2答图
在和中,
,,,
,, 四边形是平行四边形.
【变式】 C
知识点3 两组对角分别相等的四边形是平行四边形
例3 证明: ,,,
, ,.
同理可证,, 四边形是平行四边形.
知识点 对角线互相平分的四边形是平行四边形
例4 证明:在和中,,
,,
,同理可证,, 四边形是平行四边形.
【变式】 (1) 证明: 四边形是平行四边形,,.
,,,,
四边形是平行四边形.
(2) 解: ,.
平分,,
,.
,,
是线段的垂直平分线,.
,是等边三角形,
,
.
知识点5 一组对边平行且相等的四边形是平行四边形
例5 证明:如答图,连接.
例5答图
,,
在和中,
,,,
四边形是平行四边形.
例6 (1) 证明: 四边形是平行四边形,,.
,分别是边,的中点,,,.
又, 四边形是平行四边形.
同理可证,四边形是平行四边形,
(2) 证明: 四边形是平行四边形,.
同理可证,, 四边形是平行四边形.
(3) 解:四边形仍为平行四边形.理由如下:
如答图,分别过点,作,,分别交,的延长线于点,.
四边形是平行四边形,.
又,,.
在和中,
,.
,,,.
又, 四边形是平行四边形.
四边形是平行四边形,,.
,.
又, 四边形是平行四边形.
, 四边形仍为平行四边形.
例6答图
课堂检测 习题巩固
1.D 2.B
3.(答案不唯一)
4.证明:,,
,.
在和中,
,
,
四边形是平行四边形.
第2课时 三角形的中位线
课堂探究 例题点拨
知识点1 三角形的中位线的证明
例1 证明:如答图,延长到点,使,连接,,.
例1答图
,,
四边形是平行四边形,.
,
四边形是平行四边形,.
又,,.
知识点2 三角形的中位线的运用
例2 证明:,,分别为,,的中点,
,为的中位线.
,, 四边形是平行四边形.
【点悟】 三角形的中位线为证明几何中的平行关系、线段的倍分关系提供了新的依据,所以在处理相关几何问题时,若遇到中点或中位线时,可以联想中位线的性质,或通过作辅助线构造中位线,为求解问题提供方便.
【变式】 解:四边形是平行四边形.证明如下:
如答图,连接.
变式答图
点,分别是,的中点,
,.
同理,得,,
, 四边形是平行四边形.
课堂检测 习题巩固
1.B 2.B
3.80
4.10
5.证明:,平分,
为边上的中线,为的中点.
,为的中点.
为的中位线,.
第1课时 平行四边形的判定
课堂探究 例题点拨
知识点1 两组对边分别平行的四边形是平行四边形
例1 如图,,分别是的边,上的点,且.
求证:.
知识点2 两组对边分别相等的四边形是平行四边形
例2 证明:两组对边分别相等的四边形是平行四边形.
已知:在四边形中,,.
求证:四边形是平行四边形.
【变式】 在四边形中,,.若 ,则的度数为( )
A. B. C. D.
知识点3 两组对角分别相等的四边形是平行四边形
例3 证明:两组对角分别相等的四边形是平行四边形.
已知:如图,在四边形中,,.
求证:四边形是平行四边形.
知识点 对角线互相平分的四边形是平行四边形
例4 证明:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形中,,.
求证:四边形是平行四边形.
【变式】 如图,在中,对角线,相交于点,,,为直线上的两个动点(点,始终在的外部),连接,,,,,.
(1) 求证:四边形是平行四边形;
(2) 若平分, ,求四边形的周长.
知识点5 一组对边平行且相等的四边形是平行四边形
例5 证明:一组对边平行且相等的四边形是平行四边形.
已知:如图,在四边形中,,.
求证:四边形是平行四边形.
例6 (教材P47例4变式)如图,在中,如果,分别是边,的中点,交于点,交于点.
(1) 求证:四边形是平行四边形,四边形是平行四边形.
(2) 求证:四边形是平行四边形.
(3) 若将“,分别是,的中点”改为“点,分别在,上,且”,四边形是否仍为平行四边形?若是平行四边形,请说明理由;若不是平行四边形,请画图举反例说明.
课堂检测 习题巩固
1.如图,,要使四边形成为平行四边形,还需要添加的条件是( )
第1题图
A. B. C. D.
2.下面给出的是四边形中,,,的度数比,其中能判断四边形是平行四边形的是( )
A. B. C. D.
3.如图,四边形的对角线相交于点,,请添加一个条件:____________________________(只添一个即可),使四边形是平行四边形.
第3题图
4.如图,,,且,求证:四边形是平行四边形.
第2课时 三角形的中位线
课堂探究 例题点拨
知识点1 三角形的中位线的证明
例1 (教材P48探究)如图,,分别为的边,的中点,求证:,.
知识点2 三角形的中位线的运用
例2 如图,在中,,,分别为边,,的中点.
求证:四边形是平行四边形.
【变式】 如图,任意作一个四边形,并将其四边的中点依次连接起来,得到一个新的四边形,这个新的四边形的形状有什么特征?请证明你的结论.
课堂检测 习题巩固
1.如图,在等边中,点,分别是,的中点,则的度数为( )
第1题图
A. B. C. D.
2.如图,在中,,,,分别是,,,的中点.若,则( )
第2题图
A.4.5 B.6 C.7 D.8
3.[2024海南]如图是跷跷板示意图,支柱经过的中点,与地面垂直于点,,当跷跷板的一端着地时,另一端离地面的高度为__.
第3题图
4.如图,在中,对角线,相交于点,是的中点,,则的长为__.
第4题图
5.如图,在中,平分,,.求证:.
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
课堂探究 例题点拨
知识点1 两组对边分别平行的四边形是平行四边形
例1 证明: 四边形是平行四边形,
,.
,,.
, 四边形是平行四边形,.
知识点2 两组对边分别相等的四边形是平行四边形
例2 证明:如答图,连接.
例2答图
在和中,
,,,
,, 四边形是平行四边形.
【变式】 C
知识点3 两组对角分别相等的四边形是平行四边形
例3 证明: ,,,
, ,.
同理可证,, 四边形是平行四边形.
知识点 对角线互相平分的四边形是平行四边形
例4 证明:在和中,,
,,
,同理可证,, 四边形是平行四边形.
【变式】 (1) 证明: 四边形是平行四边形,,.
,,,,
四边形是平行四边形.
(2) 解: ,.
平分,,
,.
,,
是线段的垂直平分线,.
,是等边三角形,
,
.
知识点5 一组对边平行且相等的四边形是平行四边形
例5 证明:如答图,连接.
例5答图
,,
在和中,
,,,
四边形是平行四边形.
例6 (1) 证明: 四边形是平行四边形,,.
,分别是边,的中点,,,.
又, 四边形是平行四边形.
同理可证,四边形是平行四边形,
(2) 证明: 四边形是平行四边形,.
同理可证,, 四边形是平行四边形.
(3) 解:四边形仍为平行四边形.理由如下:
如答图,分别过点,作,,分别交,的延长线于点,.
四边形是平行四边形,.
又,,.
在和中,
,.
,,,.
又, 四边形是平行四边形.
四边形是平行四边形,,.
,.
又, 四边形是平行四边形.
, 四边形仍为平行四边形.
例6答图
课堂检测 习题巩固
1.D 2.B
3.(答案不唯一)
4.证明:,,
,.
在和中,
,
,
四边形是平行四边形.
第2课时 三角形的中位线
课堂探究 例题点拨
知识点1 三角形的中位线的证明
例1 证明:如答图,延长到点,使,连接,,.
例1答图
,,
四边形是平行四边形,.
,
四边形是平行四边形,.
又,,.
知识点2 三角形的中位线的运用
例2 证明:,,分别为,,的中点,
,为的中位线.
,, 四边形是平行四边形.
【点悟】 三角形的中位线为证明几何中的平行关系、线段的倍分关系提供了新的依据,所以在处理相关几何问题时,若遇到中点或中位线时,可以联想中位线的性质,或通过作辅助线构造中位线,为求解问题提供方便.
【变式】 解:四边形是平行四边形.证明如下:
如答图,连接.
变式答图
点,分别是,的中点,
,.
同理,得,,
, 四边形是平行四边形.
课堂检测 习题巩固
1.B 2.B
3.80
4.10
5.证明:,平分,
为边上的中线,为的中点.
,为的中点.
为的中位线,.
