18.2.1 矩形 分层训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 18.2.1 矩形 分层训练(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 161.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:42:09 | ||
图片预览



文档简介
18.2 特殊的平行四边形
18.2.1 矩形
第1课时 矩形的性质
A组·基础达标 逐点击破
知识点1 矩形的概念与性质
1.对于任意的矩形,下列说法一定正确的是( )
A.对角线垂直且相等
B.四边都互相垂直
C.四个角都相等
D.是轴对称图形,但不是中心对称图形
2.[2024成都]如图,在矩形中,对角线与相交于点,则下列结论一定正确的是( )
第2题图
A. B.
C. D.
3.[2024甘肃]如图,在矩形中,对角线与相交于点, ,,则的长为( )
第3题图
A.6 B.5 C.4 D.3
4.[2022邵阳]已知矩形的一边长为,一条对角线的长为,则矩形的面积为__.
5.[2022吉林]如图,在矩形中,对角线,相交于点,是边的中点,点在对角线上,且,连接.若,则________.
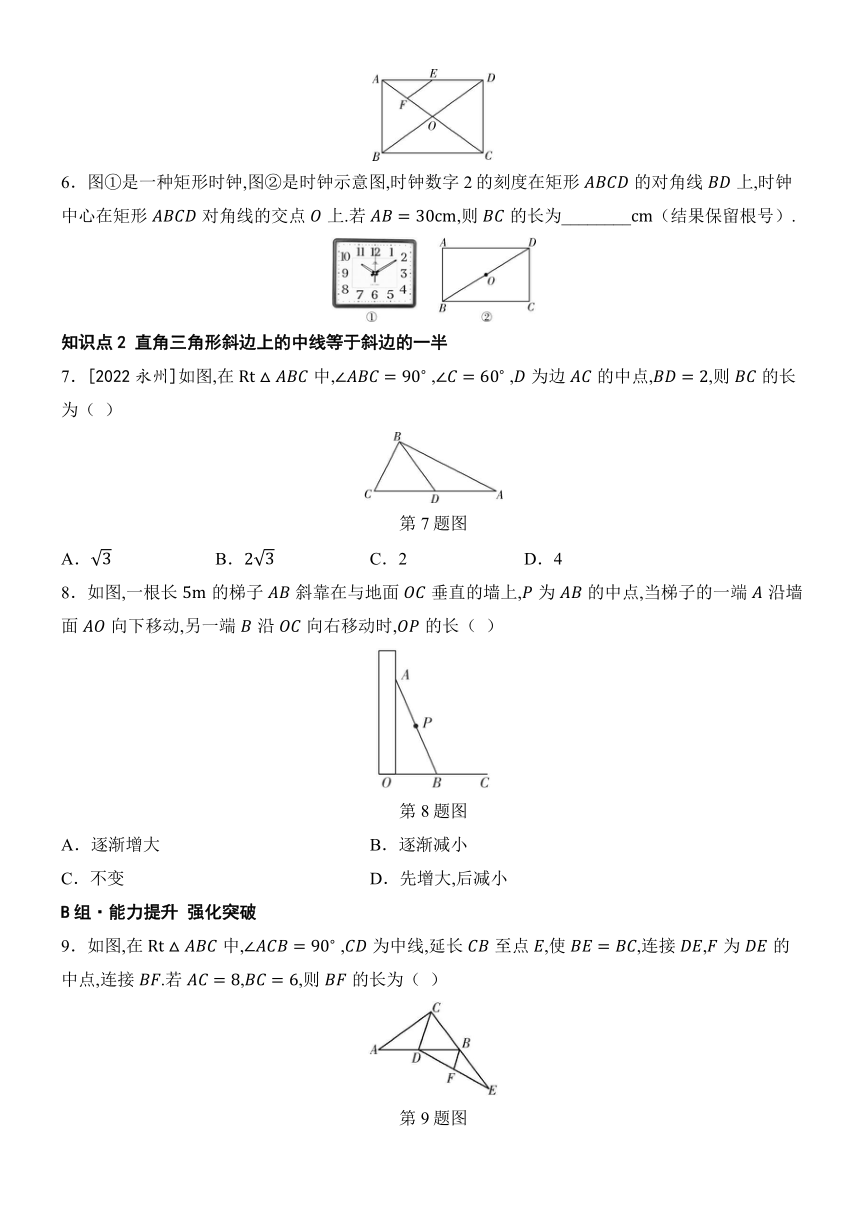
6.图①是一种矩形时钟,图②是时钟示意图,时钟数字2的刻度在矩形的对角线上,时钟中心在矩形对角线的交点上.若,则的长为________(结果保留根号).
知识点2 直角三角形斜边上的中线等于斜边的一半
7.[2022永州]如图,在中, , ,为边的中点,,则的长为( )
第7题图
A. B. C.2 D.4
8.如图,一根长的梯子斜靠在与地面垂直的墙上,为的中点,当梯子的一端沿墙面向下移动,另一端沿向右移动时,的长( )
第8题图
A.逐渐增大 B.逐渐减小
C.不变 D.先增大,后减小
B组·能力提升 强化突破
9.如图,在中, ,为中线,延长至点,使,连接,为的中点,连接.若,,则的长为( )
第9题图
A.2 B.2.5 C.3 D.4
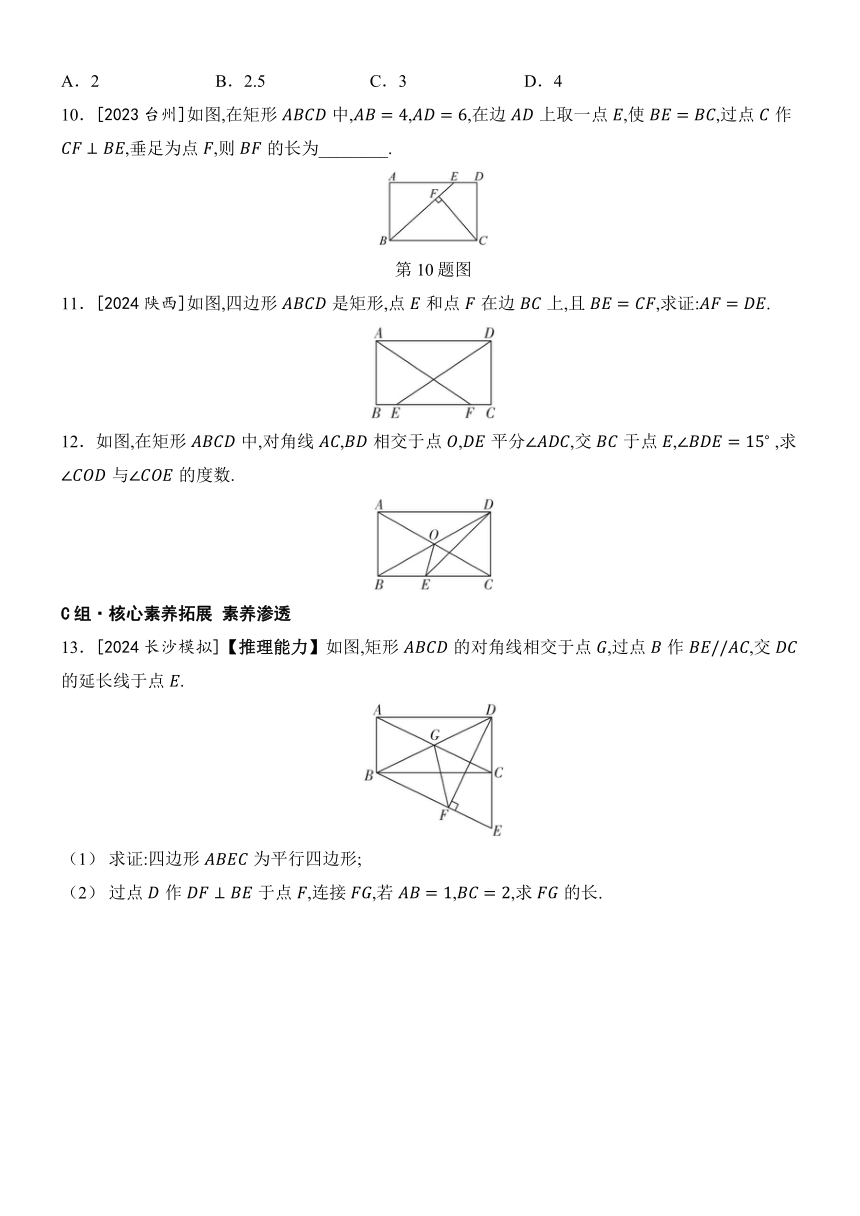
10.[2023台州]如图,在矩形中,,,在边上取一点,使,过点作,垂足为点,则的长为________.
第10题图
11.[2024陕西]如图,四边形是矩形,点和点在边上,且,求证:.
12.如图,在矩形中,对角线,相交于点,平分,交于点, ,求与的度数.
C组·核心素养拓展 素养渗透
13.[2024长沙模拟]【推理能力】如图,矩形的对角线相交于点,过点作,交的延长线于点.
(1) 求证:四边形为平行四边形;
(2) 过点作于点,连接,若,,求的长.
18.2 特殊的平行四边形
18.2.1 矩形
第1课时 矩形的性质
A组·基础达标 逐点击破
知识点1 矩形的概念与性质
1.C 2.C 3.C
4.48
5.
6.
知识点2 直角三角形斜边上的中线等于斜边的一半
7.C 8.C
B组·能力提升 强化突破
9.B
10.
11.证明: 四边形是矩形,
, .
,
,即.
在和中,
,.
12.解:四边形是矩形,平分,, ,,
,.
, .
又 矩形的对角线互相平分且相等,
,是等边三角形,
,, .
,.
.
C组·核心素养拓展 素养渗透
13.(1) 证明: 四边形是矩形,
,即.
又,
四边形为平行四边形.
(2) 解:四边形是矩形,
,,是的中点.
在中,
,
.
, ,
.
第2课时 矩形的判定
A组·基础达标 逐点击破
知识点1 有一个角是直角的平行四边形是矩形
1.如图是一个平行四边形的活动框架,对角线是两根皮筋.若改变框架的形状,则 也随之变化,两条对角线的长度也在发生改变.当________时,两条对角线的长度相等.
2.[2024长沙模拟]如图,在中,过点作于点,点在边上,且,连接.求证:四边形是矩形.
知识点2 对角线相等的平行四边形是矩形
3.[2024泸州]已知四边形是平行四边形,下列条件中,不能判定为矩形的是( )
A. B. C. D.
4.[2022泰州改编]如图,线段与分别为的中位线与中线.
(1) 求证:四边形是平行四边形;
(2) 当线段与满足数量关系为______________时,四边形为矩形.
知识点3 有三个角是直角的四边形是矩形
5.在四边形中,,则四边形__(填“是”或“不是”)矩形,依据是____________________________________.
6.如图,在中,,平分交于点,平分,于点.求证:四边形是矩形.
B组·能力提升 强化突破
7.[2024贵州]如图,四边形的对角线与相交于点,, ,有下列条件:,.
(1) 请从以上①②中任选1个作为条件,求证:四边形是矩形;
(2) 在(1)的条件下,若,,求四边形的面积.
8.[2023内江]如图,在中,是的中点,是的中点,过点作交的延长线于点.
(1) 求证:;
(2) 连接,若,求证:四边形是矩形.
C组·核心素养拓展 素养渗透
9.[2024长沙模拟]【几何直观,推理能力】如图,为中的一条射线,点在边上,于点,交于点,交于点,于点,交于点,连接交于点.
(1) 求证:四边形是矩形;
(2) 若,试探究与之间的数量关系,并说明理由.
第2课时 矩形的判定
A组·基础达标 逐点击破
知识点1 有一个角是直角的平行四边形是矩形
1.
2.证明: 四边形是平行四边形,
,.
,
,即,
四边形是平行四边形.
又, ,
四边形是矩形.
知识点2 对角线相等的平行四边形是矩形
3.D
4.(1) 证明:与分别为的中位线与中线,
,,分别为,,的中点,
,,,
,
四边形是平行四边形.
(2)
知识点3 有三个角是直角的四边形是矩形
5.是; 有三个角是直角的四边形是矩形
6.证明::平分,平分,
,.
,
,即 .
,平分,
,即 .
, ,
,
四边形是矩形.
B组·能力提升 强化突破
7.(1) 解:选择①,证明:,,
四边形是平行四边形.
,
四边形是矩形.
选择②,证明:,,
四边形是平行四边形.
,
四边形是矩形.
(2) 四边形是矩形,
.
,,
,
四边形的面积为.
8.(1) 证明:,
,.
又是的中点,
,
,
.
又是的中点,
,
.
(2) ,,
四边形是平行四边形.
,是的中点,
,即 ,
四边形是矩形.
C组·核心素养拓展 素养渗透
9.(1) 证明:,,
, .
,,
,
四边形是平行四边形.
,
,
四边形是矩形.
(2) 解:.理由如下:
四边形是矩形,
,
.
又,,
.
,.
,
,
,
即.
18.2.1 矩形
第1课时 矩形的性质
A组·基础达标 逐点击破
知识点1 矩形的概念与性质
1.对于任意的矩形,下列说法一定正确的是( )
A.对角线垂直且相等
B.四边都互相垂直
C.四个角都相等
D.是轴对称图形,但不是中心对称图形
2.[2024成都]如图,在矩形中,对角线与相交于点,则下列结论一定正确的是( )
第2题图
A. B.
C. D.
3.[2024甘肃]如图,在矩形中,对角线与相交于点, ,,则的长为( )
第3题图
A.6 B.5 C.4 D.3
4.[2022邵阳]已知矩形的一边长为,一条对角线的长为,则矩形的面积为__.
5.[2022吉林]如图,在矩形中,对角线,相交于点,是边的中点,点在对角线上,且,连接.若,则________.
6.图①是一种矩形时钟,图②是时钟示意图,时钟数字2的刻度在矩形的对角线上,时钟中心在矩形对角线的交点上.若,则的长为________(结果保留根号).
知识点2 直角三角形斜边上的中线等于斜边的一半
7.[2022永州]如图,在中, , ,为边的中点,,则的长为( )
第7题图
A. B. C.2 D.4
8.如图,一根长的梯子斜靠在与地面垂直的墙上,为的中点,当梯子的一端沿墙面向下移动,另一端沿向右移动时,的长( )
第8题图
A.逐渐增大 B.逐渐减小
C.不变 D.先增大,后减小
B组·能力提升 强化突破
9.如图,在中, ,为中线,延长至点,使,连接,为的中点,连接.若,,则的长为( )
第9题图
A.2 B.2.5 C.3 D.4
10.[2023台州]如图,在矩形中,,,在边上取一点,使,过点作,垂足为点,则的长为________.
第10题图
11.[2024陕西]如图,四边形是矩形,点和点在边上,且,求证:.
12.如图,在矩形中,对角线,相交于点,平分,交于点, ,求与的度数.
C组·核心素养拓展 素养渗透
13.[2024长沙模拟]【推理能力】如图,矩形的对角线相交于点,过点作,交的延长线于点.
(1) 求证:四边形为平行四边形;
(2) 过点作于点,连接,若,,求的长.
18.2 特殊的平行四边形
18.2.1 矩形
第1课时 矩形的性质
A组·基础达标 逐点击破
知识点1 矩形的概念与性质
1.C 2.C 3.C
4.48
5.
6.
知识点2 直角三角形斜边上的中线等于斜边的一半
7.C 8.C
B组·能力提升 强化突破
9.B
10.
11.证明: 四边形是矩形,
, .
,
,即.
在和中,
,.
12.解:四边形是矩形,平分,, ,,
,.
, .
又 矩形的对角线互相平分且相等,
,是等边三角形,
,, .
,.
.
C组·核心素养拓展 素养渗透
13.(1) 证明: 四边形是矩形,
,即.
又,
四边形为平行四边形.
(2) 解:四边形是矩形,
,,是的中点.
在中,
,
.
, ,
.
第2课时 矩形的判定
A组·基础达标 逐点击破
知识点1 有一个角是直角的平行四边形是矩形
1.如图是一个平行四边形的活动框架,对角线是两根皮筋.若改变框架的形状,则 也随之变化,两条对角线的长度也在发生改变.当________时,两条对角线的长度相等.
2.[2024长沙模拟]如图,在中,过点作于点,点在边上,且,连接.求证:四边形是矩形.
知识点2 对角线相等的平行四边形是矩形
3.[2024泸州]已知四边形是平行四边形,下列条件中,不能判定为矩形的是( )
A. B. C. D.
4.[2022泰州改编]如图,线段与分别为的中位线与中线.
(1) 求证:四边形是平行四边形;
(2) 当线段与满足数量关系为______________时,四边形为矩形.
知识点3 有三个角是直角的四边形是矩形
5.在四边形中,,则四边形__(填“是”或“不是”)矩形,依据是____________________________________.
6.如图,在中,,平分交于点,平分,于点.求证:四边形是矩形.
B组·能力提升 强化突破
7.[2024贵州]如图,四边形的对角线与相交于点,, ,有下列条件:,.
(1) 请从以上①②中任选1个作为条件,求证:四边形是矩形;
(2) 在(1)的条件下,若,,求四边形的面积.
8.[2023内江]如图,在中,是的中点,是的中点,过点作交的延长线于点.
(1) 求证:;
(2) 连接,若,求证:四边形是矩形.
C组·核心素养拓展 素养渗透
9.[2024长沙模拟]【几何直观,推理能力】如图,为中的一条射线,点在边上,于点,交于点,交于点,于点,交于点,连接交于点.
(1) 求证:四边形是矩形;
(2) 若,试探究与之间的数量关系,并说明理由.
第2课时 矩形的判定
A组·基础达标 逐点击破
知识点1 有一个角是直角的平行四边形是矩形
1.
2.证明: 四边形是平行四边形,
,.
,
,即,
四边形是平行四边形.
又, ,
四边形是矩形.
知识点2 对角线相等的平行四边形是矩形
3.D
4.(1) 证明:与分别为的中位线与中线,
,,分别为,,的中点,
,,,
,
四边形是平行四边形.
(2)
知识点3 有三个角是直角的四边形是矩形
5.是; 有三个角是直角的四边形是矩形
6.证明::平分,平分,
,.
,
,即 .
,平分,
,即 .
, ,
,
四边形是矩形.
B组·能力提升 强化突破
7.(1) 解:选择①,证明:,,
四边形是平行四边形.
,
四边形是矩形.
选择②,证明:,,
四边形是平行四边形.
,
四边形是矩形.
(2) 四边形是矩形,
.
,,
,
四边形的面积为.
8.(1) 证明:,
,.
又是的中点,
,
,
.
又是的中点,
,
.
(2) ,,
四边形是平行四边形.
,是的中点,
,即 ,
四边形是矩形.
C组·核心素养拓展 素养渗透
9.(1) 证明:,,
, .
,,
,
四边形是平行四边形.
,
,
四边形是矩形.
(2) 解:.理由如下:
四边形是矩形,
,
.
又,,
.
,.
,
,
,
即.
