18.2.2 菱形 知识点分类训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 18.2.2 菱形 知识点分类训练(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:51:45 | ||
图片预览



文档简介
18.2.2 菱形
第1课时 菱形的性质
课堂探究 例题点拨
知识点1 菱形的概念与性质
例1 证明:菱形的两条对角线互相垂直平分,且每条对角线平分一组对角.
已知:四边形是菱形,对角线,相交于点.
求证:,,,平分和,平分和.
【变式】 定义:有一条对角线平分一组对角的四边形叫做“筝形”.
(1) 如图①,在四边形中,,.求证:四边形是“筝形”.
(2) 下列关于“筝形”的性质表述正确的是____(填写所有正确结论的序号).
①“筝形”的对角线互相垂直平分;
②“筝形”中至少有一对对角相等;
③“筝形”是轴对称图形;
④“筝形”的面积等于两条对角线长的积的一半.
(3) 如图,在“筝形”中,,若 , ,,请求出对角线的长.
例2 如图,在菱形中,,分别是,的中点,连接,和有怎样的数量关系?请说明理由.
知识点2 菱形的面积
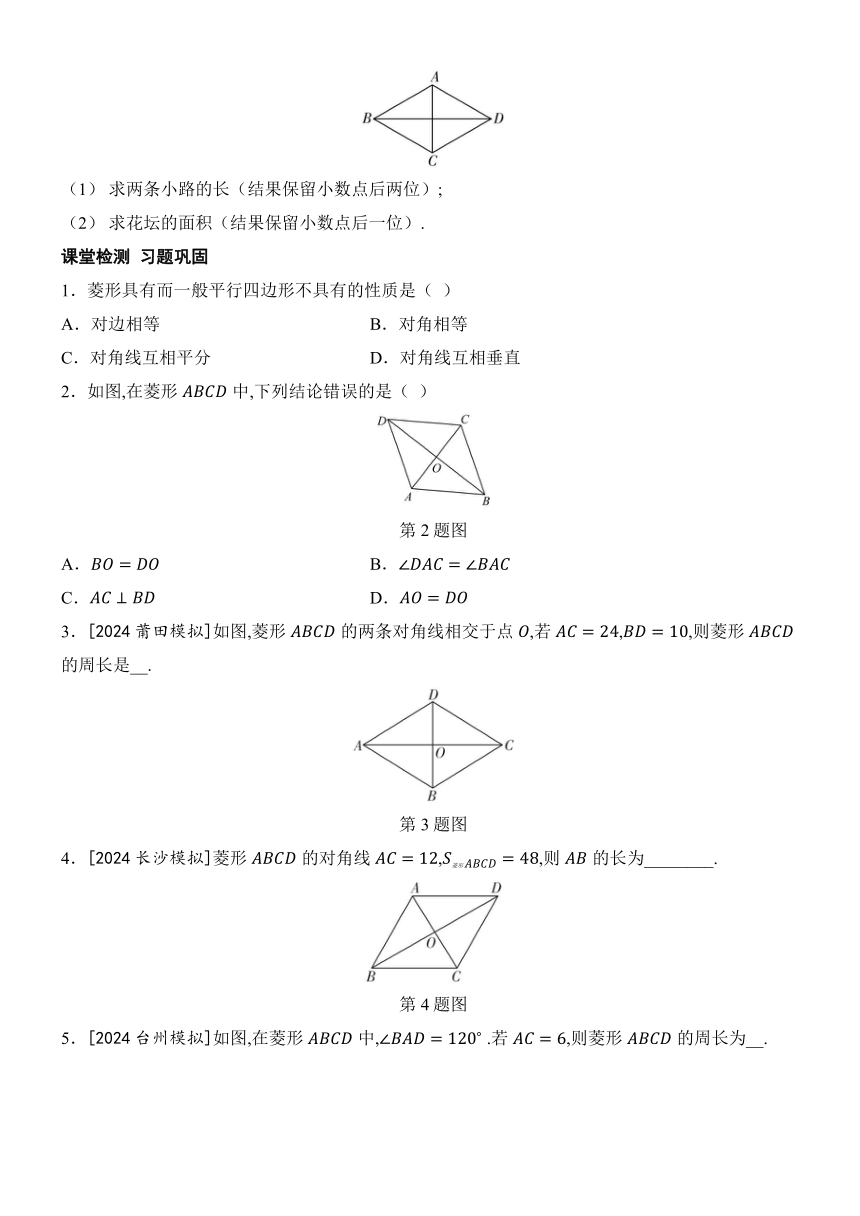
例3 如图,菱形花坛的边长为, ,沿着菱形的对角线修建了两条小路和.
(1) 求两条小路的长(结果保留小数点后两位);
(2) 求花坛的面积(结果保留小数点后一位).
课堂检测 习题巩固
1.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
2.如图,在菱形中,下列结论错误的是( )
第2题图
A. B.
C. D.
3.[2024莆田模拟]如图,菱形的两条对角线相交于点,若,,则菱形的周长是__.
第3题图
4.[2024长沙模拟]菱形的对角线,,则的长为________.
第4题图
5.[2024台州模拟]如图,在菱形中, .若,则菱形的周长为__.
第5题图
6.如图,已知四边形是菱形, ,.
(1) 求的度数;
(2) 求的长.
第2课时 菱形的判定
课堂探究 例题点拨
知识点1 有一组邻边相等的平行四边形是菱形
例1 如图,在中,是的平分线,交于点,交于点.求证:四边形是菱形.
知识点2 对角线互相垂直的平行四边形是菱形
例2 (教材P57思考)证明:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
已知:如图,在中,对角线,相交于点,____________.
求证:__________________________.
例3 (教材P57例4变式)如图,的两条对角线,相交于点,,,.求证:四边形是菱形.
知识点3 四条边相等的四边形是菱形
例4 如图,在中,是边上的一点,连接.将沿翻折,使点落在点处,当时,求证:四边形是菱形.
课堂检测 习题巩固
1.如图,已知四边形是平行四边形,要使它成为菱形,则需要添加的条件可以是( )
第1题图
A. B.
C. D.
2.如图,在中,平分,,则的周长为( )
第2题图
A.4 B.6 C.8 D.12
3.如图,在四边形中,,,.求证:四边形是菱形.
4.如图,在中,对角线,相交于点,已知, .
(1) 求证:是菱形;
(2) 求的长.
18.2.2 菱形
第1课时 菱形的性质
课堂探究 例题点拨
知识点1 菱形的概念与性质
例1 证明: 四边形是菱形,
四边形是平行四边形,,
,,,
,平分和,平分和.
【变式】 (1) 证明:在和中,
,
,,
四边形是“筝形”.
(2) ②③④
(3) 解:如答图,过点作,交的延长线于点.
四边形是“筝形”,,
, ,
,.
,,
,解得.
, ,.
变式答图
例2 解:.理由如下:
四边形是菱形,
,,.
又,分别是,的中点,
,,.
,.
知识点2 菱形的面积
例3 (1) 解:设与相交于点(图略).
菱形花坛的边长为, ,
, ,
是等边三角形,
,.
,
.
两条小路的长分别约为,.
(2) 由(1)得,花坛的面积为.
课堂检测 习题巩固
1.D 2.D
3.52
4.
5.24
6.(1) 解: 四边形是菱形, ,
,
.
(2) 如答图,连接交于点.
,.
,.
,.
第6题答图
第2课时 菱形的判定
课堂探究 例题点拨
知识点1 有一组邻边相等的平行四边形是菱形
例1 证明:,,
四边形是平行四边形,.
是的平分线,,
, 四边形是菱形.
知识点2 对角线互相垂直的平行四边形是菱形
例2 ; 四边形是菱形; 证明: 四边形是平行四边形,.
于点,
, 四边形是菱形.
例3 证明: 四边形是平行四边形,
,.
,
为直角三角形,且 ,
即, 四边形是菱形.
【点悟】 已知四边形是平行四边形,只需证明“对角线互相垂直”或“有一组邻边相等”即可判定四边形是菱形.
知识点3 四条边相等的四边形是菱形
例4 证明:由折叠的性质,得,,.
,,,
,,
四边形是菱形.
【点悟】 如果四边形中相等的边数较多,可考虑直接利用四条边相等来判定四边形是菱形.
课堂检测 习题巩固
1.A 2.C
3.证明:,,
四边形是平行四边形.
,
四边形是菱形.
4.(1) 证明:, ,
是等边三角形.
,是菱形.
(2) 解:在菱形中,,.
,,
,.
第1课时 菱形的性质
课堂探究 例题点拨
知识点1 菱形的概念与性质
例1 证明:菱形的两条对角线互相垂直平分,且每条对角线平分一组对角.
已知:四边形是菱形,对角线,相交于点.
求证:,,,平分和,平分和.
【变式】 定义:有一条对角线平分一组对角的四边形叫做“筝形”.
(1) 如图①,在四边形中,,.求证:四边形是“筝形”.
(2) 下列关于“筝形”的性质表述正确的是____(填写所有正确结论的序号).
①“筝形”的对角线互相垂直平分;
②“筝形”中至少有一对对角相等;
③“筝形”是轴对称图形;
④“筝形”的面积等于两条对角线长的积的一半.
(3) 如图,在“筝形”中,,若 , ,,请求出对角线的长.
例2 如图,在菱形中,,分别是,的中点,连接,和有怎样的数量关系?请说明理由.
知识点2 菱形的面积
例3 如图,菱形花坛的边长为, ,沿着菱形的对角线修建了两条小路和.
(1) 求两条小路的长(结果保留小数点后两位);
(2) 求花坛的面积(结果保留小数点后一位).
课堂检测 习题巩固
1.菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等
C.对角线互相平分 D.对角线互相垂直
2.如图,在菱形中,下列结论错误的是( )
第2题图
A. B.
C. D.
3.[2024莆田模拟]如图,菱形的两条对角线相交于点,若,,则菱形的周长是__.
第3题图
4.[2024长沙模拟]菱形的对角线,,则的长为________.
第4题图
5.[2024台州模拟]如图,在菱形中, .若,则菱形的周长为__.
第5题图
6.如图,已知四边形是菱形, ,.
(1) 求的度数;
(2) 求的长.
第2课时 菱形的判定
课堂探究 例题点拨
知识点1 有一组邻边相等的平行四边形是菱形
例1 如图,在中,是的平分线,交于点,交于点.求证:四边形是菱形.
知识点2 对角线互相垂直的平行四边形是菱形
例2 (教材P57思考)证明:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
已知:如图,在中,对角线,相交于点,____________.
求证:__________________________.
例3 (教材P57例4变式)如图,的两条对角线,相交于点,,,.求证:四边形是菱形.
知识点3 四条边相等的四边形是菱形
例4 如图,在中,是边上的一点,连接.将沿翻折,使点落在点处,当时,求证:四边形是菱形.
课堂检测 习题巩固
1.如图,已知四边形是平行四边形,要使它成为菱形,则需要添加的条件可以是( )
第1题图
A. B.
C. D.
2.如图,在中,平分,,则的周长为( )
第2题图
A.4 B.6 C.8 D.12
3.如图,在四边形中,,,.求证:四边形是菱形.
4.如图,在中,对角线,相交于点,已知, .
(1) 求证:是菱形;
(2) 求的长.
18.2.2 菱形
第1课时 菱形的性质
课堂探究 例题点拨
知识点1 菱形的概念与性质
例1 证明: 四边形是菱形,
四边形是平行四边形,,
,,,
,平分和,平分和.
【变式】 (1) 证明:在和中,
,
,,
四边形是“筝形”.
(2) ②③④
(3) 解:如答图,过点作,交的延长线于点.
四边形是“筝形”,,
, ,
,.
,,
,解得.
, ,.
变式答图
例2 解:.理由如下:
四边形是菱形,
,,.
又,分别是,的中点,
,,.
,.
知识点2 菱形的面积
例3 (1) 解:设与相交于点(图略).
菱形花坛的边长为, ,
, ,
是等边三角形,
,.
,
.
两条小路的长分别约为,.
(2) 由(1)得,花坛的面积为.
课堂检测 习题巩固
1.D 2.D
3.52
4.
5.24
6.(1) 解: 四边形是菱形, ,
,
.
(2) 如答图,连接交于点.
,.
,.
,.
第6题答图
第2课时 菱形的判定
课堂探究 例题点拨
知识点1 有一组邻边相等的平行四边形是菱形
例1 证明:,,
四边形是平行四边形,.
是的平分线,,
, 四边形是菱形.
知识点2 对角线互相垂直的平行四边形是菱形
例2 ; 四边形是菱形; 证明: 四边形是平行四边形,.
于点,
, 四边形是菱形.
例3 证明: 四边形是平行四边形,
,.
,
为直角三角形,且 ,
即, 四边形是菱形.
【点悟】 已知四边形是平行四边形,只需证明“对角线互相垂直”或“有一组邻边相等”即可判定四边形是菱形.
知识点3 四条边相等的四边形是菱形
例4 证明:由折叠的性质,得,,.
,,,
,,
四边形是菱形.
【点悟】 如果四边形中相等的边数较多,可考虑直接利用四条边相等来判定四边形是菱形.
课堂检测 习题巩固
1.A 2.C
3.证明:,,
四边形是平行四边形.
,
四边形是菱形.
4.(1) 证明:, ,
是等边三角形.
,是菱形.
(2) 解:在菱形中,,.
,,
,.
