19.2.3 一次函数与方程、不等式 分层训练(含答案) 初中数学人教版八年级下册
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式 分层训练(含答案) 初中数学人教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 127.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:48:07 | ||
图片预览


文档简介
19.2.3 一次函数与方程、不等式
A组·基础达标 逐点击破
知识点1 一次函数与一元一次方程
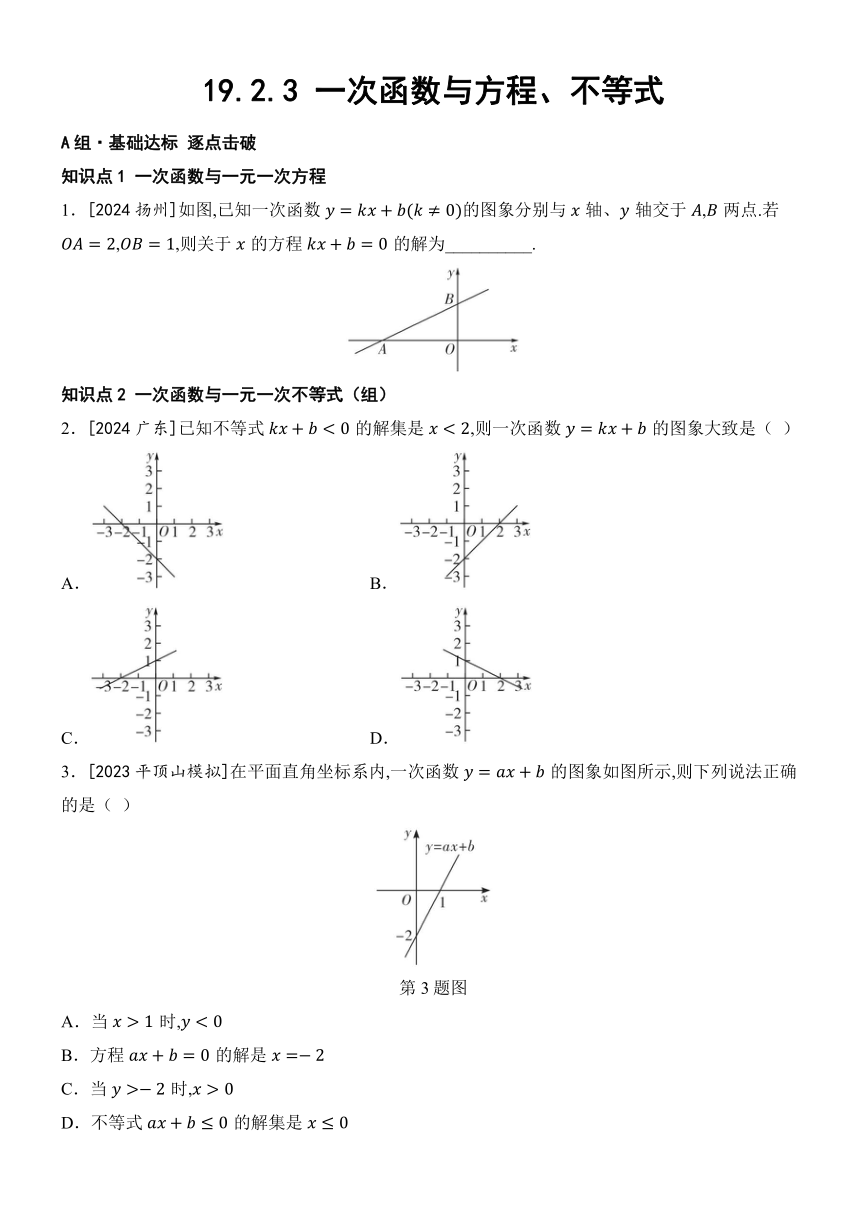
1.[2024扬州]如图,已知一次函数的图象分别与轴、轴交于,两点.若,,则关于的方程的解为__________.
知识点2 一次函数与一元一次不等式(组)
2.[2024广东]已知不等式的解集是,则一次函数的图象大致是( )
A. B.
C. D.
3.[2023平顶山模拟]在平面直角坐标系内,一次函数的图象如图所示,则下列说法正确的是( )
第3题图
A.当时,
B.方程的解是
C.当时,
D.不等式的解集是
4.如图,直线与直线相交于点,根据图象可知,关于的不等式的解集是________.
第4题图
知识点3 一次函数与二元一次方程组
5.[2024内蒙古]点在直线上,坐标是二元一次方程的解,则点的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.[2023巴中模拟]如图,直线交轴、轴分别于,两点,直线交轴、轴分别于,两点,直线,相交于点.
(1) 方程组的解是__________________________________________;
(2) 求直线,与轴围成的三角形的面积;
(3) 过点的直线把的面积两等分,直接写出这条直线的解析式.
B组·能力提升 强化突破
7.[2023宁夏]在同一平面直角坐标系中,一次函数与的图象如图所示,则下列说法错误的是( )
A.随的增大而增大
B.
C.当时,
D.关于,的方程组的解为
8.如图,点,的坐标分别为,,直线与轴交于点,与轴交于点.
(1) 设直线的函数解析式为,求直线与的交点的坐标;
(2) 四边形的面积是____.
9.[2024北京]在平面直角坐标系中,函数与的图象交于点.
(1) 求,的值;
(2) 当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,直接写出的取值范围.
C组·核心素养拓展 素养渗透
10.[2023丽水]【应用意识】为促进生产,某公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.根据图中信息,解答下列问题:
(1) 直接写出当员工生产多少件产品时,两种方案付给的报酬一样多;
(2) 求方案二关于的函数解析式;
(3) 如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
19.2.3 一次函数与方程、不等式
A组·基础达标 逐点击破
知识点1 一次函数与一元一次方程
1.
知识点2 一次函数与一元一次不等式(组)
2.B 3.C
4.
知识点3 一次函数与二元一次方程组
5.D
6.(1)
(2) 解:把分别代入和,
解得和,
,.
,
直线,与轴围成的三角形的面积为.
(3) 这条直线的解析式为.
B组·能力提升 强化突破
7.C
8.(1) 解:把,代入,得解得
直线的函数解析式为.
联立
解得
点的坐标为.
(2) 4
9.(1) 解: 直线过点,
,解得.
将点代入,得,
解得.
,.
(2) 当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,如答图.
第9题答图
.
的取值范围是.
C组·核心素养拓展 素养渗透
10.(1) 解:当员工生产30件产品时,两种方案付给的报酬一样多.
(2) 设方案二的函数解析式为.观察图象得,方案二的函数图象经过点,.
将,代入函数解析式,得解得
方案二关于的函数解析式为.
(3) 由两种方案的函数图象相交于点可知:
若每月生产产品不足30件,则选择方案二;若每月生产产品为30件,两种方案报酬相同,可以任选一种;若每月生产产品超过30件,则选择方案一.
A组·基础达标 逐点击破
知识点1 一次函数与一元一次方程
1.[2024扬州]如图,已知一次函数的图象分别与轴、轴交于,两点.若,,则关于的方程的解为__________.
知识点2 一次函数与一元一次不等式(组)
2.[2024广东]已知不等式的解集是,则一次函数的图象大致是( )
A. B.
C. D.
3.[2023平顶山模拟]在平面直角坐标系内,一次函数的图象如图所示,则下列说法正确的是( )
第3题图
A.当时,
B.方程的解是
C.当时,
D.不等式的解集是
4.如图,直线与直线相交于点,根据图象可知,关于的不等式的解集是________.
第4题图
知识点3 一次函数与二元一次方程组
5.[2024内蒙古]点在直线上,坐标是二元一次方程的解,则点的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.[2023巴中模拟]如图,直线交轴、轴分别于,两点,直线交轴、轴分别于,两点,直线,相交于点.
(1) 方程组的解是__________________________________________;
(2) 求直线,与轴围成的三角形的面积;
(3) 过点的直线把的面积两等分,直接写出这条直线的解析式.
B组·能力提升 强化突破
7.[2023宁夏]在同一平面直角坐标系中,一次函数与的图象如图所示,则下列说法错误的是( )
A.随的增大而增大
B.
C.当时,
D.关于,的方程组的解为
8.如图,点,的坐标分别为,,直线与轴交于点,与轴交于点.
(1) 设直线的函数解析式为,求直线与的交点的坐标;
(2) 四边形的面积是____.
9.[2024北京]在平面直角坐标系中,函数与的图象交于点.
(1) 求,的值;
(2) 当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,直接写出的取值范围.
C组·核心素养拓展 素养渗透
10.[2023丽水]【应用意识】为促进生产,某公司提供了两种付给员工月报酬的方案,如图所示,员工可以任选一种方案与公司签订合同.根据图中信息,解答下列问题:
(1) 直接写出当员工生产多少件产品时,两种方案付给的报酬一样多;
(2) 求方案二关于的函数解析式;
(3) 如果你是劳务服务部门的工作人员,你如何指导员工根据自己的生产能力选择方案.
19.2.3 一次函数与方程、不等式
A组·基础达标 逐点击破
知识点1 一次函数与一元一次方程
1.
知识点2 一次函数与一元一次不等式(组)
2.B 3.C
4.
知识点3 一次函数与二元一次方程组
5.D
6.(1)
(2) 解:把分别代入和,
解得和,
,.
,
直线,与轴围成的三角形的面积为.
(3) 这条直线的解析式为.
B组·能力提升 强化突破
7.C
8.(1) 解:把,代入,得解得
直线的函数解析式为.
联立
解得
点的坐标为.
(2) 4
9.(1) 解: 直线过点,
,解得.
将点代入,得,
解得.
,.
(2) 当时,对于的每一个值,函数的值既大于函数的值,也大于函数的值,如答图.
第9题答图
.
的取值范围是.
C组·核心素养拓展 素养渗透
10.(1) 解:当员工生产30件产品时,两种方案付给的报酬一样多.
(2) 设方案二的函数解析式为.观察图象得,方案二的函数图象经过点,.
将,代入函数解析式,得解得
方案二关于的函数解析式为.
(3) 由两种方案的函数图象相交于点可知:
若每月生产产品不足30件,则选择方案二;若每月生产产品为30件,两种方案报酬相同,可以任选一种;若每月生产产品超过30件,则选择方案一.
