20.1.1 平均数 分层训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 20.1.1 平均数 分层训练(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 208.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:47:11 | ||
图片预览

文档简介
第二十章 数据的分析
20.1 数据的集中趋势
20.1.1 平均数
第1课时 加权平均数
A组·基础达标 逐点击破
知识点1 算术平均数
1.[2022内江]某店今年月新能源汽车的销量(辆数)分别如下:25,33,36,31,40,这组数据的平均数是( )
A.34 B.33 C.32.5 D.31
2.[2024宿迁]已知一组数据6,8,10,的平均数是9,则的值为__.
知识点2 加权平均数
3.小明记录了某市五月份某周每天的日最高气温如下表所示:
最高气温/ 22 26 28 29
天数 1 2 1 3
则这周最高气温的平均数是( )
A. B. C. D.
4.[2024南充]学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占,投球技能占计算选手的综合成绩.若选手李林控球技能得90分、投球技能得80分,则李林的综合成绩为( )
A.170分 B.86分 C.85分 D.84分
5.[2022乐山]李老师参加本校青年数学教师优质课比赛,笔试得90分,微型课得92分,教学反思得88分.按照如图所示的笔试、微型课、教学反思的权重,李老师的综合成绩为( )
A.88分 B.90分 C.91分 D.92分
6.[2023邵阳]下表是小红参加一次“阳光体育”活动比赛的得分情况:
项目 跑步 花样跳绳 跳绳
得分 90 80 70
评总分时,按跑步占,花样跳绳占,跳绳占考评,则小红的最终得分为__分.
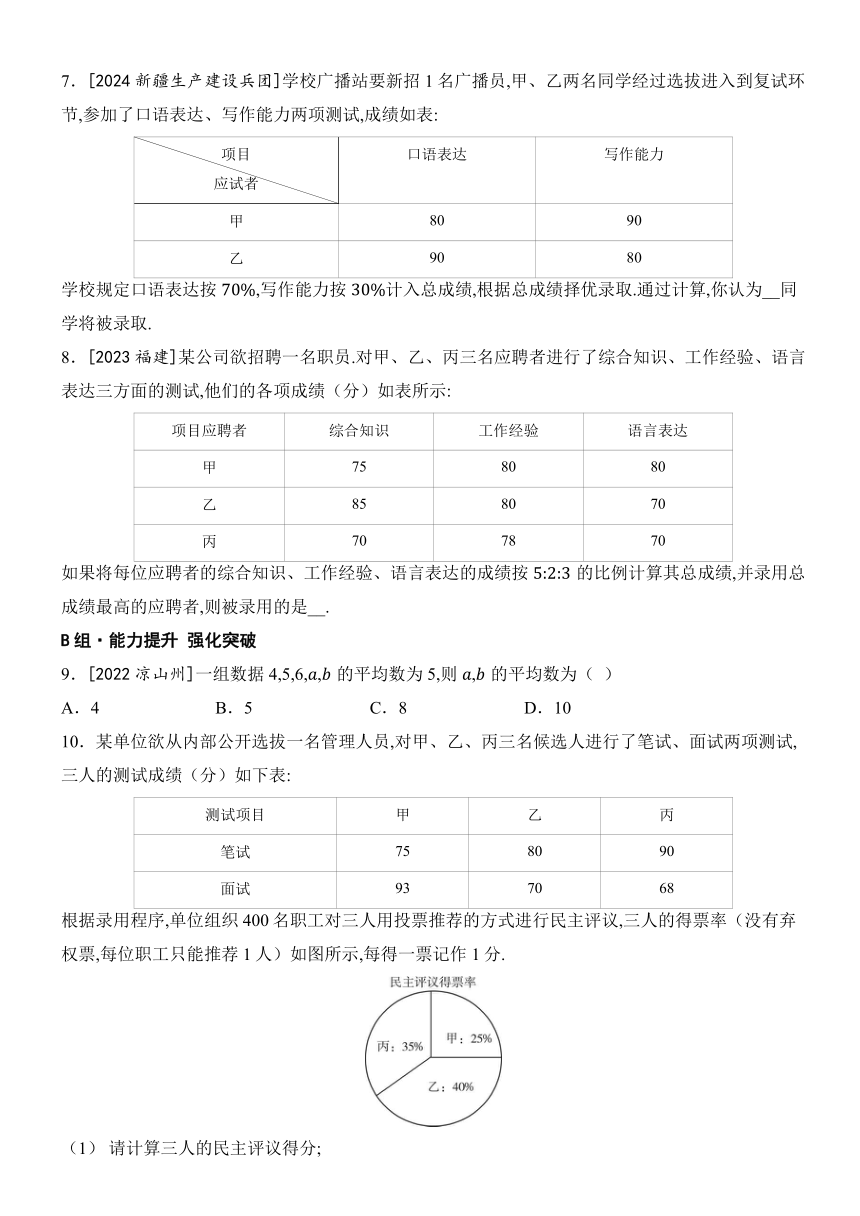
7.[2024新疆生产建设兵团]学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入到复试环节,参加了口语表达、写作能力两项测试,成绩如表:
项目 应试者 口语表达 写作能力
甲 80 90
乙 90 80
学校规定口语表达按,写作能力按计入总成绩,根据总成绩择优录取.通过计算,你认为__同学将被录取.
8.[2023福建]某公司欲招聘一名职员.对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达三方面的测试,他们的各项成绩(分)如表所示:
项目应聘者 综合知识 工作经验 语言表达
甲 75 80 80
乙 85 80 70
丙 70 78 70
如果将每位应聘者的综合知识、工作经验、语言表达的成绩按的比例计算其总成绩,并录用总成绩最高的应聘者,则被录用的是__.
B组·能力提升 强化突破
9.[2022凉山州]一组数据4,5,6,,的平均数为5,则,的平均数为( )
A.4 B.5 C.8 D.10
10.某单位欲从内部公开选拔一名管理人员,对甲、乙、丙三名候选人进行了笔试、面试两项测试,三人的测试成绩(分)如下表:
测试项目 甲 乙 丙
笔试 75 80 90
面试 93 70 68
根据录用程序,单位组织400名职工对三人用投票推荐的方式进行民主评议,三人的得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分.
(1) 请计算三人的民主评议得分;
(2) 根据实际需要,单位将笔试、面试、民主评议三项的得分按的比例确定个人成绩(精确到0.1分),那么谁将被成功选拔?
C组·核心素养拓展 素养渗透
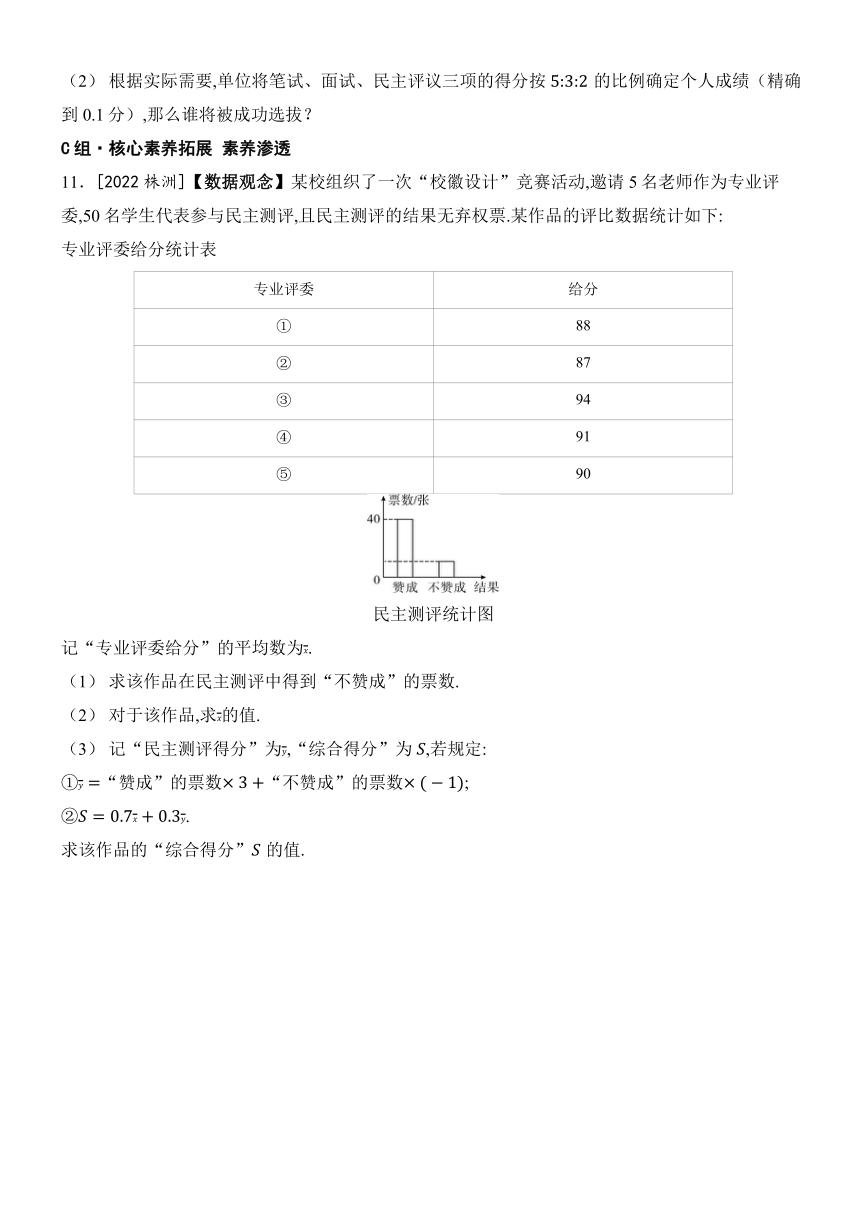
11.[2022株洲]【数据观念】某校组织了一次“校徽设计”竞赛活动,邀请5名老师作为专业评委,50名学生代表参与民主测评,且民主测评的结果无弃权票.某作品的评比数据统计如下:
专业评委给分统计表
专业评委 给分
① 88
② 87
③ 94
④ 91
⑤ 90
民主测评统计图
记“专业评委给分”的平均数为.
(1) 求该作品在民主测评中得到“不赞成”的票数.
(2) 对于该作品,求的值.
(3) 记“民主测评得分”为,“综合得分”为,若规定:
①“赞成”的票数“不赞成”的票数;
②.
求该作品的“综合得分”的值.
第2课时 用样本平均数估计总体平均数
A组·基础达标 逐点击破
知识点1 组中值与平均数
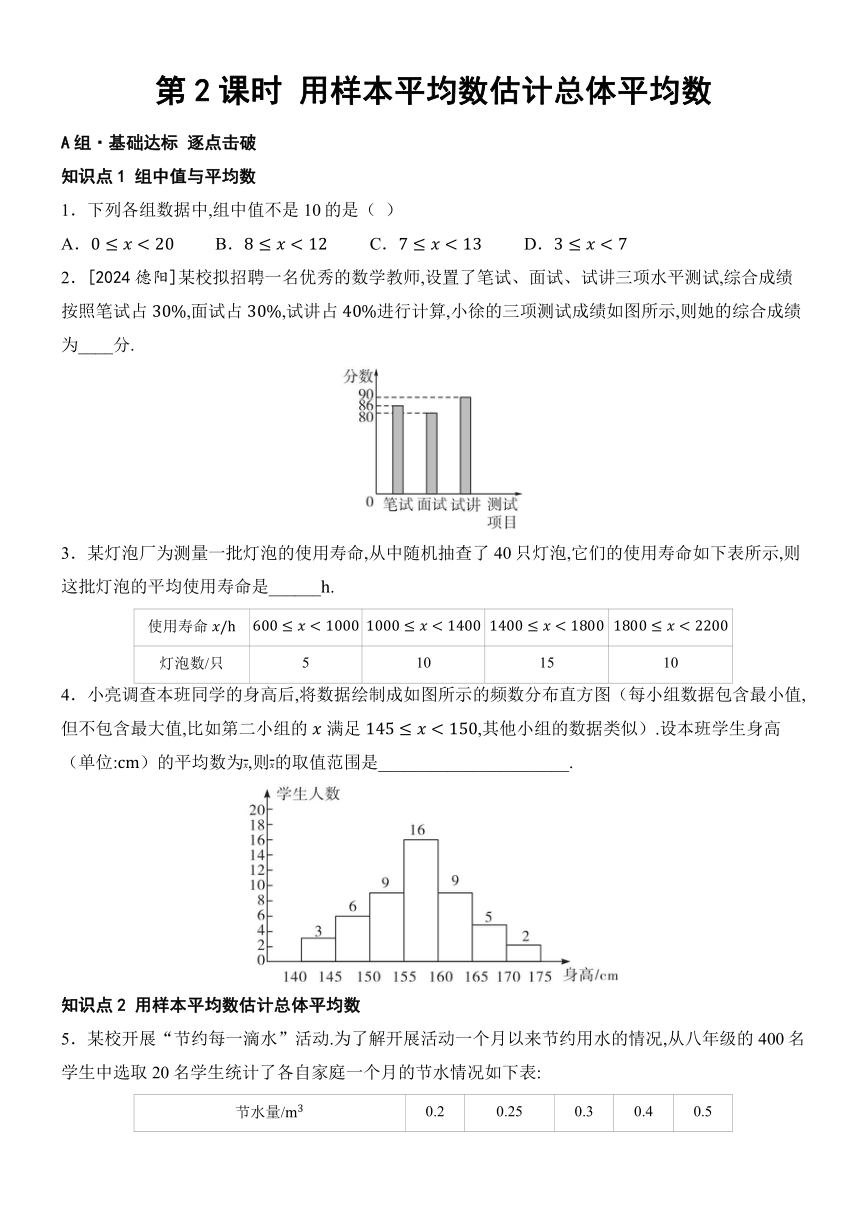
1.下列各组数据中,组中值不是10的是( )
A. B. C. D.
2.[2024德阳]某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占,面试占,试讲占进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为____分.
3.某灯泡厂为测量一批灯泡的使用寿命,从中随机抽查了40只灯泡,它们的使用寿命如下表所示,则这批灯泡的平均使用寿命是______.
使用寿命
灯泡数/只 5 10 15 10
4.小亮调查本班同学的身高后,将数据绘制成如图所示的频数分布直方图(每小组数据包含最小值,但不包含最大值,比如第二小组的满足,其他小组的数据类似).设本班学生身高(单位:)的平均数为,则的取值范围是______________________.
知识点2 用样本平均数估计总体平均数
5.某校开展“节约每一滴水”活动.为了解开展活动一个月以来节约用水的情况,从八年级的400名学生中选取20名学生统计了各自家庭一个月的节水情况如下表:
节水量/ 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
估计这400名学生的家庭一个月节约用水的总量是( )
A. B. C. D.
6.[2024苏州]某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1) 将图①中的条形统计图补充完整(画图并标注相应数据);
(2) 图②中项目对应的圆心角的度数为________;
(3) 根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
B组·能力提升 强化突破
7.[2024枣庄]某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用表示),并将其分成如下四组:,,,.
下面给出了部分信息:
的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1) 请补全频数分布直方图;
(2) 请估计全校1 000名学生的模型设计成绩不低于80分的人数;
(3) 根据活动要求,学校将模型设计成绩、科技小论文成绩按的比例确定这次活动各人的综合成绩.某班甲、乙两名学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙哪名学生的综合成绩更高?
C组·核心素养拓展 素养渗透
8.[2024福建]【数据观念】已知A,B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3 000人,数学平均分为90分;乙类学校有考生2 000人,数学平均分为80分.
(1) 求A地考生的数学平均分.
(2) 若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明;若不能,请举例说明.
第二十章 数据的分析
20.1 数据的集中趋势
20.1.1 平均数
第1课时 加权平均数
A组·基础达标 逐点击破
知识点1 算术平均数
1.B
2.12
知识点2 加权平均数
3.B 4.B 5.C
6.83
7.乙
[解析]根据题意可知,甲同学的成绩为(分);乙同学的成绩为(分), 乙同学将被录取.
8.乙
[解析]由题意,可得
甲的成绩为,
乙的成绩为,
丙的成绩为.
, 乙将被录取.
B组·能力提升 强化突破
9.B
10.(1) 解:甲:(分),
乙:(分),
丙:(分).
(2) 甲:(分),
乙:(分),
丙:(分).
丙的成绩最高, 丙将被成功选拔.
C组·核心素养拓展 素养渗透
11.(1) 解:该作品在民主测评中得到“不赞成”的票数为(张).
(2) (分).
(3) (分);
(分).
第2课时 用样本平均数估计总体平均数
A组·基础达标 逐点击破
知识点1 组中值与平均数
1.D
2.85.8
3.1 500
4.
知识点2 用样本平均数估计总体平均数
5.A
6.(1) 解:此次调查的总人数为,
选择项目D的人数为,
补全条形统计图如答图:
第6题答图
(2)
(3) (名).
答:估计本校七年级800名学生中选择项目B(乒乓球)的人数为240.
B组·能力提升 强化突破
7.(1) 解:,而有20人,
的成绩有(人),
补全图形如答图:
第7题答图
(2) 全校1 000名学生的模型设计成绩不低于80分的人数为.
(3) 甲的成绩为(分),
乙的成绩为(分).
,
甲的综合成绩更高.
C组·核心素养拓展 素养渗透
8.(1) 解:由题意,得A地考生的数学平均分为(分).
(2) 不能.举例如下:
如B地甲类学校有考生1 000人,乙类学校有考生3 000人,则B地考生的数学平均分为(分).
, 不能判断B地考生数学平均分一定比A地考生数学平均分高.(答案不唯一,合理即可)
20.1 数据的集中趋势
20.1.1 平均数
第1课时 加权平均数
A组·基础达标 逐点击破
知识点1 算术平均数
1.[2022内江]某店今年月新能源汽车的销量(辆数)分别如下:25,33,36,31,40,这组数据的平均数是( )
A.34 B.33 C.32.5 D.31
2.[2024宿迁]已知一组数据6,8,10,的平均数是9,则的值为__.
知识点2 加权平均数
3.小明记录了某市五月份某周每天的日最高气温如下表所示:
最高气温/ 22 26 28 29
天数 1 2 1 3
则这周最高气温的平均数是( )
A. B. C. D.
4.[2024南充]学校举行篮球技能大赛,评委从控球技能和投球技能两方面为选手打分,各项成绩均按百分制计,然后再按控球技能占,投球技能占计算选手的综合成绩.若选手李林控球技能得90分、投球技能得80分,则李林的综合成绩为( )
A.170分 B.86分 C.85分 D.84分
5.[2022乐山]李老师参加本校青年数学教师优质课比赛,笔试得90分,微型课得92分,教学反思得88分.按照如图所示的笔试、微型课、教学反思的权重,李老师的综合成绩为( )
A.88分 B.90分 C.91分 D.92分
6.[2023邵阳]下表是小红参加一次“阳光体育”活动比赛的得分情况:
项目 跑步 花样跳绳 跳绳
得分 90 80 70
评总分时,按跑步占,花样跳绳占,跳绳占考评,则小红的最终得分为__分.
7.[2024新疆生产建设兵团]学校广播站要新招1名广播员,甲、乙两名同学经过选拔进入到复试环节,参加了口语表达、写作能力两项测试,成绩如表:
项目 应试者 口语表达 写作能力
甲 80 90
乙 90 80
学校规定口语表达按,写作能力按计入总成绩,根据总成绩择优录取.通过计算,你认为__同学将被录取.
8.[2023福建]某公司欲招聘一名职员.对甲、乙、丙三名应聘者进行了综合知识、工作经验、语言表达三方面的测试,他们的各项成绩(分)如表所示:
项目应聘者 综合知识 工作经验 语言表达
甲 75 80 80
乙 85 80 70
丙 70 78 70
如果将每位应聘者的综合知识、工作经验、语言表达的成绩按的比例计算其总成绩,并录用总成绩最高的应聘者,则被录用的是__.
B组·能力提升 强化突破
9.[2022凉山州]一组数据4,5,6,,的平均数为5,则,的平均数为( )
A.4 B.5 C.8 D.10
10.某单位欲从内部公开选拔一名管理人员,对甲、乙、丙三名候选人进行了笔试、面试两项测试,三人的测试成绩(分)如下表:
测试项目 甲 乙 丙
笔试 75 80 90
面试 93 70 68
根据录用程序,单位组织400名职工对三人用投票推荐的方式进行民主评议,三人的得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分.
(1) 请计算三人的民主评议得分;
(2) 根据实际需要,单位将笔试、面试、民主评议三项的得分按的比例确定个人成绩(精确到0.1分),那么谁将被成功选拔?
C组·核心素养拓展 素养渗透
11.[2022株洲]【数据观念】某校组织了一次“校徽设计”竞赛活动,邀请5名老师作为专业评委,50名学生代表参与民主测评,且民主测评的结果无弃权票.某作品的评比数据统计如下:
专业评委给分统计表
专业评委 给分
① 88
② 87
③ 94
④ 91
⑤ 90
民主测评统计图
记“专业评委给分”的平均数为.
(1) 求该作品在民主测评中得到“不赞成”的票数.
(2) 对于该作品,求的值.
(3) 记“民主测评得分”为,“综合得分”为,若规定:
①“赞成”的票数“不赞成”的票数;
②.
求该作品的“综合得分”的值.
第2课时 用样本平均数估计总体平均数
A组·基础达标 逐点击破
知识点1 组中值与平均数
1.下列各组数据中,组中值不是10的是( )
A. B. C. D.
2.[2024德阳]某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占,面试占,试讲占进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为____分.
3.某灯泡厂为测量一批灯泡的使用寿命,从中随机抽查了40只灯泡,它们的使用寿命如下表所示,则这批灯泡的平均使用寿命是______.
使用寿命
灯泡数/只 5 10 15 10
4.小亮调查本班同学的身高后,将数据绘制成如图所示的频数分布直方图(每小组数据包含最小值,但不包含最大值,比如第二小组的满足,其他小组的数据类似).设本班学生身高(单位:)的平均数为,则的取值范围是______________________.
知识点2 用样本平均数估计总体平均数
5.某校开展“节约每一滴水”活动.为了解开展活动一个月以来节约用水的情况,从八年级的400名学生中选取20名学生统计了各自家庭一个月的节水情况如下表:
节水量/ 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
估计这400名学生的家庭一个月节约用水的总量是( )
A. B. C. D.
6.[2024苏州]某校计划在七年级开展阳光体育锻炼活动,开设以下五个球类项目:A(羽毛球),B(乒乓球),C(篮球),D(排球),(足球),要求每位学生必须参加,且只能选择其中一个项目.为了了解学生对这五个项目的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,对调查所得到的数据进行整理、描述和分析,部分信息如下:
根据上信息,解决下列问题:
(1) 将图①中的条形统计图补充完整(画图并标注相应数据);
(2) 图②中项目对应的圆心角的度数为________;
(3) 根据抽样调查结果,请估计本校七年级800名学生中选择项目B(乒乓球)的人数.
B组·能力提升 强化突破
7.[2024枣庄]某学校开展了“校园科技节”活动,活动包含模型设计、科技小论文两个项目.为了解学生的模型设计水平,从全校学生的模型设计成绩中随机抽取部分学生的模型设计成绩(成绩为百分制,用表示),并将其分成如下四组:,,,.
下面给出了部分信息:
的成绩为:81,81,82,82,83,83,84,84,84,85,86,86,86,87,88,88,88,89,89,89.
根据以上信息解决下列问题:
(1) 请补全频数分布直方图;
(2) 请估计全校1 000名学生的模型设计成绩不低于80分的人数;
(3) 根据活动要求,学校将模型设计成绩、科技小论文成绩按的比例确定这次活动各人的综合成绩.某班甲、乙两名学生的模型设计成绩与科技小论文成绩(单位:分)如下:
模型设计 科技小论文
甲的成绩 94 90
乙的成绩 90 95
通过计算,甲、乙哪名学生的综合成绩更高?
C组·核心素养拓展 素养渗透
8.[2024福建]【数据观念】已知A,B两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3 000人,数学平均分为90分;乙类学校有考生2 000人,数学平均分为80分.
(1) 求A地考生的数学平均分.
(2) 若B地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B地考生数学平均分一定比A地考生数学平均分高?若能,请给予证明;若不能,请举例说明.
第二十章 数据的分析
20.1 数据的集中趋势
20.1.1 平均数
第1课时 加权平均数
A组·基础达标 逐点击破
知识点1 算术平均数
1.B
2.12
知识点2 加权平均数
3.B 4.B 5.C
6.83
7.乙
[解析]根据题意可知,甲同学的成绩为(分);乙同学的成绩为(分), 乙同学将被录取.
8.乙
[解析]由题意,可得
甲的成绩为,
乙的成绩为,
丙的成绩为.
, 乙将被录取.
B组·能力提升 强化突破
9.B
10.(1) 解:甲:(分),
乙:(分),
丙:(分).
(2) 甲:(分),
乙:(分),
丙:(分).
丙的成绩最高, 丙将被成功选拔.
C组·核心素养拓展 素养渗透
11.(1) 解:该作品在民主测评中得到“不赞成”的票数为(张).
(2) (分).
(3) (分);
(分).
第2课时 用样本平均数估计总体平均数
A组·基础达标 逐点击破
知识点1 组中值与平均数
1.D
2.85.8
3.1 500
4.
知识点2 用样本平均数估计总体平均数
5.A
6.(1) 解:此次调查的总人数为,
选择项目D的人数为,
补全条形统计图如答图:
第6题答图
(2)
(3) (名).
答:估计本校七年级800名学生中选择项目B(乒乓球)的人数为240.
B组·能力提升 强化突破
7.(1) 解:,而有20人,
的成绩有(人),
补全图形如答图:
第7题答图
(2) 全校1 000名学生的模型设计成绩不低于80分的人数为.
(3) 甲的成绩为(分),
乙的成绩为(分).
,
甲的综合成绩更高.
C组·核心素养拓展 素养渗透
8.(1) 解:由题意,得A地考生的数学平均分为(分).
(2) 不能.举例如下:
如B地甲类学校有考生1 000人,乙类学校有考生3 000人,则B地考生的数学平均分为(分).
, 不能判断B地考生数学平均分一定比A地考生数学平均分高.(答案不唯一,合理即可)
