20.2 数据的波动程度 分层训练(含答案) 初中数学人教版八年级下册
文档属性
| 名称 | 20.2 数据的波动程度 分层训练(含答案) 初中数学人教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 152.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 00:00:00 | ||
图片预览


文档简介
20.2 数据的波动程度
第1课时 方差
A组·基础达标 逐点击破
知识点1 方差的概念及计算
1.数据,,0,1,2的方差是( )
A.0 B. C.2 D.4
2.若对于一组数据,,, ,,可用如下算式计算方差:,其中5是这组数据的( )
A.最小值 B.平均数 C.中位数 D.众数
3.[2024宜宾]某校为了解九年级学生在校的锻炼情况,随机抽取10名学生,记录他们某一天在校的锻炼时间(单位:)分别为:65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是( )
A.方差为0 B.众数为75
C.中位数为77.5 D.平均数为75
4.[2023凉山州]若一组数据,,, ,的方差为2,则数据,,, ,的方差是( )
A.2 B.5 C.6 D.11
5.[2024上海]科学家同时培育了甲、乙、丙、丁四种花,从甲、乙、丙、丁中选个开花时间最短的并且最平稳的是( )
种类 甲 乙 丙 丁
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
A.甲种类 B.乙种类 C.丙种类 D.丁种类
6.[2024遂宁]体育老师要在甲和乙两人中选择1人参加篮球投篮大赛,下表是两人5次训练的成绩,从稳定的角度考虑,老师应该选__参加比赛.
甲的成绩 8 8 7 9 8
乙的成绩 6 9 7 9 9
知识点2 方差的应用
7.[2022株洲模拟]某校七年级两个班各选派6名学生参加“垃圾分类知识竞赛”,各参赛选手的成绩(分)如下(满分100分):
七(1)班:87,91,91,92,94,96;
七(2)班:84,88,90,90,91,97.
根据以上数据,解决下列问题:
(1) 七(1)班参赛选手成绩的中位数和众数分别为多少分?
(2) 七(2)班参赛选手成绩的方差为多少?
B组·能力提升 强化突破
8.某人5次射击命中的环数分别为5,10,7,,10.若这组数据的中位数为8,则这组数据的方差为____.
9.[2022常德模拟]在一次广场舞比赛中,甲、乙两个队参加表演的女演员的身高分别是:
甲队:163,165,165,164,168;
乙队:162,164,164,167,168.
(1) 求甲队女演员身高的平均数、众数.
(2) 计算两队女演员身高的方差,并判断哪个队女演员的身高更整齐?
C组·核心素养拓展 素养渗透
10.[2024河南]【数据观念】为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下:
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,解答下列问题.
(1) 这六场比赛中,得分更稳定的队员是__(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为__分.
(2) 请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3) 规定“综合得分”为平均每场得分平均每场篮板平均每场失误,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
第2课时 用样本方差估计总体方差
A组·基础达标 逐点击破
知识点 方差在实际生活中的应用
1.[2022株洲模拟]某校组织开展了主题为“青春齐奋进,携手向未来”的演讲比赛,七(1)班、七(2)班均有5名同学进入复赛,其中七(1)班5名同学的比赛成绩(分)如下:7,9,10,7,8.根据以上信息,解答下列问题:
(1) 七(1)班5名同学的比赛成绩的众数是____,中位数是____.
(2) 求七(1)班5名同学的比赛成绩的平均数和方差.
(3) 已知七(2)班5名同学的比赛成绩的平均数为8.4分,中位数为8分,方差为1.04.请根据统计数据进行分析,说说哪个班进入复赛的同学在比赛中的表现更优秀?
2.[2024深圳]据了解,推动“深圳”体育场馆一键预约平台是市委、市政府打造“民生幸福标杆”城市过程中的惠民利民重要举措,对满足市民健身需求、激发全民健身热情、促进体育消费等方面具有重大意义.按照符合条件的学校体育场馆和社会体育场馆“应接尽接”原则,“深圳”体育场馆一键预约平台实现了“让想运动的人找到场地,已有的体育场地得到有效利用”.
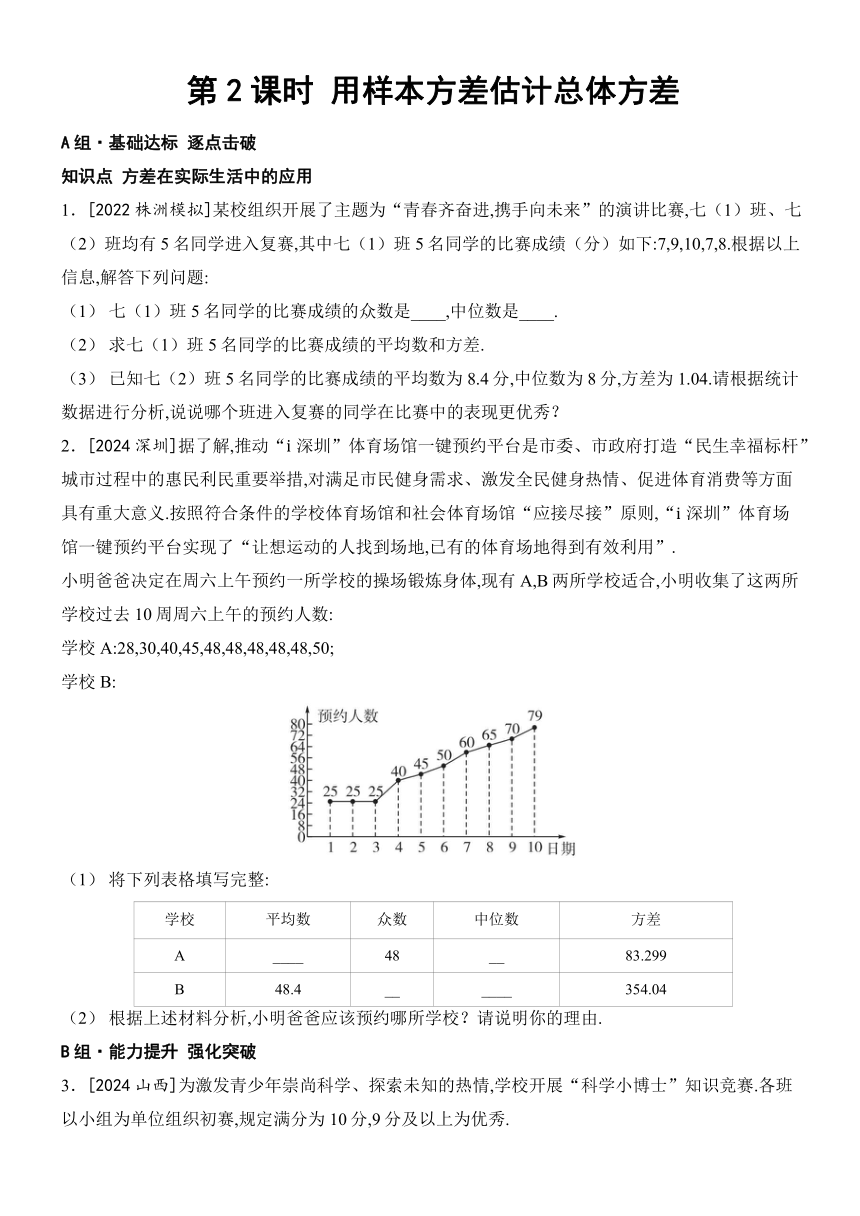
小明爸爸决定在周六上午预约一所学校的操场锻炼身体,现有A,B两所学校适合,小明收集了这两所学校过去10周周六上午的预约人数:
学校A:28,30,40,45,48,48,48,48,48,50;
学校B:
(1) 将下列表格填写完整:
学校 平均数 众数 中位数 方差
A ____ 48 __ 83.299
B 48.4 __ ____ 354.04
(2) 根据上述材料分析,小明爸爸应该预约哪所学校?请说明你的理由.
B组·能力提升 强化突破
3.[2024山西]为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
组别 平均数/分 中位数/分 众数/分 方差 优秀率
甲组 7.625 7 4.48
乙组 7.625 7 0.73
请认真阅读上述信息,解答下列问题:
(1) 填空:____,____,__________.
(2) 小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好;小夏认为小祺的观点比较片面.请结合上表中的信息帮小夏说明理由(写出两条即可).
C组·核心素养拓展 素养渗透
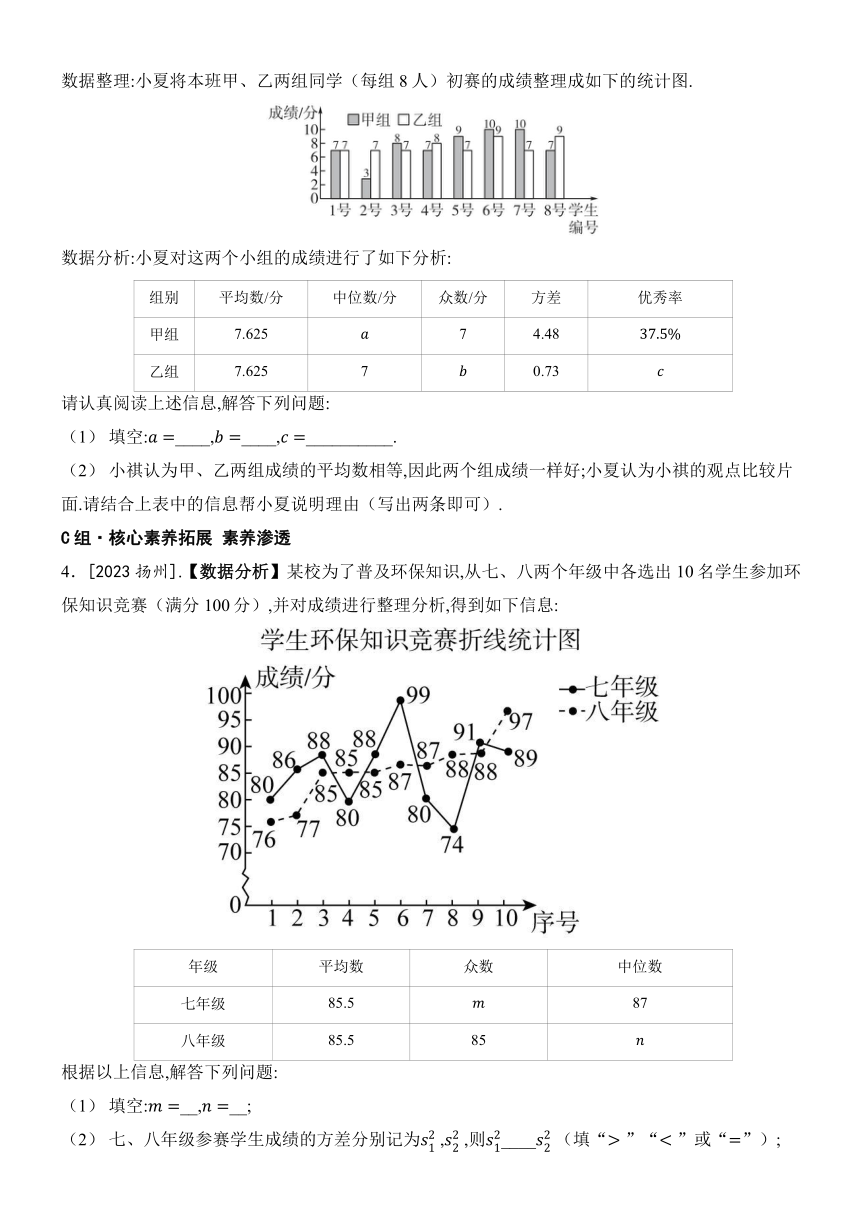
4.[2023扬州].【数据分析】某校为了普及环保知识,从七、八两个年级中各选出10名学生参加环保知识竞赛(满分100分),并对成绩进行整理分析,得到如下信息:
年级 平均数 众数 中位数
七年级 85.5 87
八年级 85.5 85
根据以上信息,解答下列问题:
(1) 填空:__,__;
(2) 七、八年级参赛学生成绩的方差分别记为 , ,则____ (填“ ”“ ”或“”);
(3) 从平均数和中位数的角度分析哪个年级参赛学生的成绩较好.
20.2 数据的波动程度
第1课时 方差
A组·基础达标 逐点击破
知识点1 方差的概念及计算
1.C 2.B 3.B 4.A 5.B
6.甲
[解析]甲的成绩的平均数是,甲的成绩的方差;
乙的成绩的平均数是,乙的成绩的方差.
, 老师应该选甲.
知识点2 方差的应用
7.(1) 解:七(1)班参赛选手成绩的中位数为(分).
出现了2次,出现的次数最多,
众数是91分.
(2) 七(2)班参赛选手成绩的平均数为
(分),
则方差为(分).
B组·能力提升 强化突破
8.3.6
9.(1) 解:,
则甲队女演员身高的平均数是.
出现了2次,出现的次数最多,
众数是.
(2) 乙队女演员身高的平均数为.
,
.
,
甲队女演员的身高更整齐.
C组·核心素养拓展 素养渗透
10.(1) 甲; 29
[解析]由折线图可得甲得分更稳定,
把乙的六次成绩按从小到大的顺序排序,第三次、第四次的成绩分别为28和30,
故中位数为.
(2) 解:甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定, 甲队员表现更好.(答案不唯一,合理即可)
(3) 解:甲的综合得分为(分),
乙的综合得分为(分).
,
乙队员表现更好.
第2课时 用样本方差估计总体方差
A组·基础达标 逐点击破
知识点 方差在实际生活中的应用
1.(1) 7; 8
[解析]将七(1)班5名同学的比赛成绩按从小到大的顺序排列为7,7,8,9,10,数据7出现了两次,次数最多,所以众数为7,第三个数是8,所以中位数为8.
(2) 解:七(1)班5名同学的比赛成绩的平均数(分),
方差.
(3) 解:七(2)班进入复赛的同学在比赛中的表现更优秀.理由如下:
七(2)班同学的成绩的平均数大于七(1)班,说明平均水平更高;方差更小,说明成绩更稳定.
七(2)班进入复赛的同学在比赛中表现更优秀.
2.(1) 43.3; 48; 25; 47.5
[解析]学校的平均数为,中位数为48;
学校的众数为25,中位数为.
(2) 解:小明爸爸应该预约A学校.理由如下:
两所学校的平均数接近,但A学校的方差小于B学校,即A学校预约人数比较稳定, 小明爸爸应该预约A学校.
B组·能力提升 强化突破
3.(1) 7.5; 7;
(2) 解:小祺的观点比较片面.
(理由不唯一)例如:①甲组成绩的优秀率为,高于乙组成绩的优秀率,
从优秀率的角度看,甲组成绩比乙组好;
②甲组成绩的中位数为,高于乙组成绩的中位数,
从中位数的角度看,甲组成绩比乙组好;
因此不能仅从平均数的角度说明两组成绩一样好,所以小祺的观点比较片面.
C组·核心素养拓展 素养渗透
4.(1) 80; 86
[解析]七年级成绩中80分出现次数最多, 众数;
将八年级成绩从小到大排列为76,77,85,85,85,87,87,88,88,97,
中位数.
(2)
[解析] 七年级的方差,
八年级的方差,
,
.
(3) 解:两个年级成绩的平均数相同,而七年级的中位数较大,
七年级的成绩较好.
第1课时 方差
A组·基础达标 逐点击破
知识点1 方差的概念及计算
1.数据,,0,1,2的方差是( )
A.0 B. C.2 D.4
2.若对于一组数据,,, ,,可用如下算式计算方差:,其中5是这组数据的( )
A.最小值 B.平均数 C.中位数 D.众数
3.[2024宜宾]某校为了解九年级学生在校的锻炼情况,随机抽取10名学生,记录他们某一天在校的锻炼时间(单位:)分别为:65,67,75,65,75,80,75,88,78,80.对这组数据判断正确的是( )
A.方差为0 B.众数为75
C.中位数为77.5 D.平均数为75
4.[2023凉山州]若一组数据,,, ,的方差为2,则数据,,, ,的方差是( )
A.2 B.5 C.6 D.11
5.[2024上海]科学家同时培育了甲、乙、丙、丁四种花,从甲、乙、丙、丁中选个开花时间最短的并且最平稳的是( )
种类 甲 乙 丙 丁
平均数 2.3 2.3 2.8 3.1
方差 1.05 0.78 1.05 0.78
A.甲种类 B.乙种类 C.丙种类 D.丁种类
6.[2024遂宁]体育老师要在甲和乙两人中选择1人参加篮球投篮大赛,下表是两人5次训练的成绩,从稳定的角度考虑,老师应该选__参加比赛.
甲的成绩 8 8 7 9 8
乙的成绩 6 9 7 9 9
知识点2 方差的应用
7.[2022株洲模拟]某校七年级两个班各选派6名学生参加“垃圾分类知识竞赛”,各参赛选手的成绩(分)如下(满分100分):
七(1)班:87,91,91,92,94,96;
七(2)班:84,88,90,90,91,97.
根据以上数据,解决下列问题:
(1) 七(1)班参赛选手成绩的中位数和众数分别为多少分?
(2) 七(2)班参赛选手成绩的方差为多少?
B组·能力提升 强化突破
8.某人5次射击命中的环数分别为5,10,7,,10.若这组数据的中位数为8,则这组数据的方差为____.
9.[2022常德模拟]在一次广场舞比赛中,甲、乙两个队参加表演的女演员的身高分别是:
甲队:163,165,165,164,168;
乙队:162,164,164,167,168.
(1) 求甲队女演员身高的平均数、众数.
(2) 计算两队女演员身高的方差,并判断哪个队女演员的身高更整齐?
C组·核心素养拓展 素养渗透
10.[2024河南]【数据观念】为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下:
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,解答下列问题.
(1) 这六场比赛中,得分更稳定的队员是__(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为__分.
(2) 请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.
(3) 规定“综合得分”为平均每场得分平均每场篮板平均每场失误,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好.
第2课时 用样本方差估计总体方差
A组·基础达标 逐点击破
知识点 方差在实际生活中的应用
1.[2022株洲模拟]某校组织开展了主题为“青春齐奋进,携手向未来”的演讲比赛,七(1)班、七(2)班均有5名同学进入复赛,其中七(1)班5名同学的比赛成绩(分)如下:7,9,10,7,8.根据以上信息,解答下列问题:
(1) 七(1)班5名同学的比赛成绩的众数是____,中位数是____.
(2) 求七(1)班5名同学的比赛成绩的平均数和方差.
(3) 已知七(2)班5名同学的比赛成绩的平均数为8.4分,中位数为8分,方差为1.04.请根据统计数据进行分析,说说哪个班进入复赛的同学在比赛中的表现更优秀?
2.[2024深圳]据了解,推动“深圳”体育场馆一键预约平台是市委、市政府打造“民生幸福标杆”城市过程中的惠民利民重要举措,对满足市民健身需求、激发全民健身热情、促进体育消费等方面具有重大意义.按照符合条件的学校体育场馆和社会体育场馆“应接尽接”原则,“深圳”体育场馆一键预约平台实现了“让想运动的人找到场地,已有的体育场地得到有效利用”.
小明爸爸决定在周六上午预约一所学校的操场锻炼身体,现有A,B两所学校适合,小明收集了这两所学校过去10周周六上午的预约人数:
学校A:28,30,40,45,48,48,48,48,48,50;
学校B:
(1) 将下列表格填写完整:
学校 平均数 众数 中位数 方差
A ____ 48 __ 83.299
B 48.4 __ ____ 354.04
(2) 根据上述材料分析,小明爸爸应该预约哪所学校?请说明你的理由.
B组·能力提升 强化突破
3.[2024山西]为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图.
数据分析:小夏对这两个小组的成绩进行了如下分析:
组别 平均数/分 中位数/分 众数/分 方差 优秀率
甲组 7.625 7 4.48
乙组 7.625 7 0.73
请认真阅读上述信息,解答下列问题:
(1) 填空:____,____,__________.
(2) 小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好;小夏认为小祺的观点比较片面.请结合上表中的信息帮小夏说明理由(写出两条即可).
C组·核心素养拓展 素养渗透
4.[2023扬州].【数据分析】某校为了普及环保知识,从七、八两个年级中各选出10名学生参加环保知识竞赛(满分100分),并对成绩进行整理分析,得到如下信息:
年级 平均数 众数 中位数
七年级 85.5 87
八年级 85.5 85
根据以上信息,解答下列问题:
(1) 填空:__,__;
(2) 七、八年级参赛学生成绩的方差分别记为 , ,则____ (填“ ”“ ”或“”);
(3) 从平均数和中位数的角度分析哪个年级参赛学生的成绩较好.
20.2 数据的波动程度
第1课时 方差
A组·基础达标 逐点击破
知识点1 方差的概念及计算
1.C 2.B 3.B 4.A 5.B
6.甲
[解析]甲的成绩的平均数是,甲的成绩的方差;
乙的成绩的平均数是,乙的成绩的方差.
, 老师应该选甲.
知识点2 方差的应用
7.(1) 解:七(1)班参赛选手成绩的中位数为(分).
出现了2次,出现的次数最多,
众数是91分.
(2) 七(2)班参赛选手成绩的平均数为
(分),
则方差为(分).
B组·能力提升 强化突破
8.3.6
9.(1) 解:,
则甲队女演员身高的平均数是.
出现了2次,出现的次数最多,
众数是.
(2) 乙队女演员身高的平均数为.
,
.
,
甲队女演员的身高更整齐.
C组·核心素养拓展 素养渗透
10.(1) 甲; 29
[解析]由折线图可得甲得分更稳定,
把乙的六次成绩按从小到大的顺序排序,第三次、第四次的成绩分别为28和30,
故中位数为.
(2) 解:甲的平均每场得分大于乙的平均每场得分,且甲的得分更稳定, 甲队员表现更好.(答案不唯一,合理即可)
(3) 解:甲的综合得分为(分),
乙的综合得分为(分).
,
乙队员表现更好.
第2课时 用样本方差估计总体方差
A组·基础达标 逐点击破
知识点 方差在实际生活中的应用
1.(1) 7; 8
[解析]将七(1)班5名同学的比赛成绩按从小到大的顺序排列为7,7,8,9,10,数据7出现了两次,次数最多,所以众数为7,第三个数是8,所以中位数为8.
(2) 解:七(1)班5名同学的比赛成绩的平均数(分),
方差.
(3) 解:七(2)班进入复赛的同学在比赛中的表现更优秀.理由如下:
七(2)班同学的成绩的平均数大于七(1)班,说明平均水平更高;方差更小,说明成绩更稳定.
七(2)班进入复赛的同学在比赛中表现更优秀.
2.(1) 43.3; 48; 25; 47.5
[解析]学校的平均数为,中位数为48;
学校的众数为25,中位数为.
(2) 解:小明爸爸应该预约A学校.理由如下:
两所学校的平均数接近,但A学校的方差小于B学校,即A学校预约人数比较稳定, 小明爸爸应该预约A学校.
B组·能力提升 强化突破
3.(1) 7.5; 7;
(2) 解:小祺的观点比较片面.
(理由不唯一)例如:①甲组成绩的优秀率为,高于乙组成绩的优秀率,
从优秀率的角度看,甲组成绩比乙组好;
②甲组成绩的中位数为,高于乙组成绩的中位数,
从中位数的角度看,甲组成绩比乙组好;
因此不能仅从平均数的角度说明两组成绩一样好,所以小祺的观点比较片面.
C组·核心素养拓展 素养渗透
4.(1) 80; 86
[解析]七年级成绩中80分出现次数最多, 众数;
将八年级成绩从小到大排列为76,77,85,85,85,87,87,88,88,97,
中位数.
(2)
[解析] 七年级的方差,
八年级的方差,
,
.
(3) 解:两个年级成绩的平均数相同,而七年级的中位数较大,
七年级的成绩较好.
