第十八章 平行四边形 知识点分类训练(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 第十八章 平行四边形 知识点分类训练(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 180.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:57:58 | ||
图片预览



文档简介
第十八章 平行四边形 复习课
整合提升 练就四能
类型之1 平行四边形的性质与判定
1.[2024株洲模拟]如图,,是平行四边形对角线上的两点,.
(1) 求证:四边形是平行四边形;
(2) 若的面积为6, ,,求的长.
2.[2024长沙模拟]如图①,在中,点在的延长线上,点在的延长线上,满足.连接,分别与,相交于点,.
(1) 求证:;
(2) 如图②,连接交于点,写出图中四对全等三角形.和除外
类型之2 三角形的中位线与直角三角形斜边上的中线
3.[2024长沙模拟]如图,在中,是边上的高,是边上的中线,,是的中点.求证:
(1) ;
(2) .
类型之3 矩形的性质与判定
4.[2023大庆]如图,在中,为线段的中点,连接,,延长,与的延长线交于点,连接, .
(1) 求证:四边形是矩形;
(2) 若,,求四边形的面积.
类型之4 菱形的性质与判定
5.[2023湘西州]如图,四边形是平行四边形,,且分别交对角线于点,,连接,.
(1) 求证:;
(2) 若,求证:四边形是菱形.
6.[2024岳阳模拟]如图,在中,,分别为,的中点,,延长交的延长线于点,连接.
(1) 求证:四边形是菱形;
(2) 若 ,判断四边形的形状,并说明理由.
类型之5 正方形的性质与判定
7.[2023攀枝花]如图,已知正方形的边长为3,是对角线上的一点,于点,于点,连接.当时,( )
A. B.2 C. D.
8.如图,四边形为正方形,为线段上一点,连接,过点作,交于点,以,为邻边作矩形,连接.
(1) 求证:矩形是正方形;
(2) 若,,求的长;
(3) 当 时,求的度数.
类型之6 中点四边形
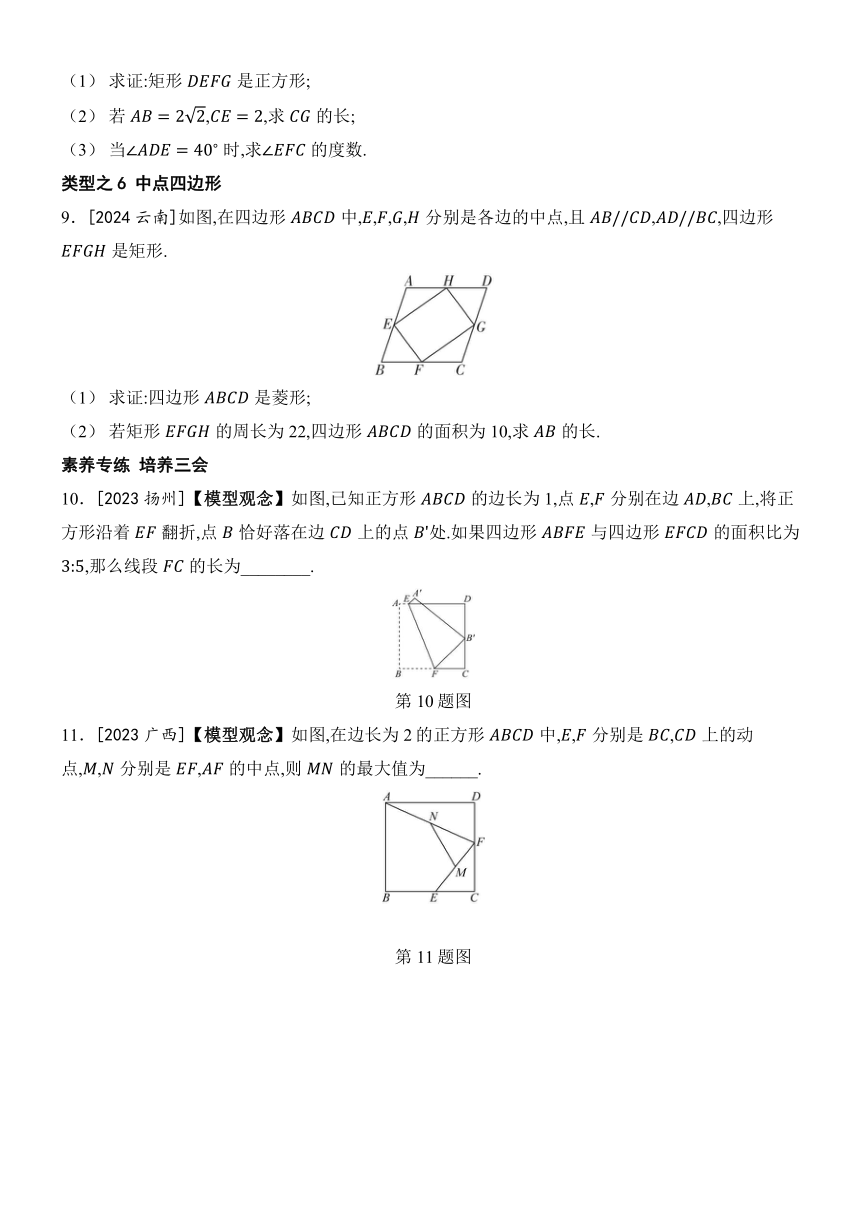
9.[2024云南]如图,在四边形中,,,,分别是各边的中点,且,,四边形是矩形.
(1) 求证:四边形是菱形;
(2) 若矩形的周长为22,四边形的面积为10,求的长.
素养专练 培养三会
10.[2023扬州]【模型观念】如图,已知正方形的边长为1,点,分别在边,上,将正方形沿着翻折,点恰好落在边上的点处.如果四边形与四边形的面积比为,那么线段的长为________.
第10题图
11.[2023广西]【模型观念】如图,在边长为2的正方形中,,分别是,上的动点,,分别是,的中点,则的最大值为______.
第11题图
本章复习课
整合提升 练就四能
类型之1 平行四边形的性质与判定
1.(1) 证明:在中,,,.
,.
在和中,
,.
又,
四边形是平行四边形.
(2) 解:如答图,过点作,交的延长线于点.
第1题答图
,,
.
, ,
.
2.(1) 证明:在中,,,
,.
在和中,
,
.
(2) 解:四对全等三角形:、、、.
类型之2 三角形的中位线与直角三角形斜边上的中线
3.(1) 证明:如答图,连接.
第3题答图
是边上的高, .
是边上的中线,即是的中点,
.
,.
又是的中点..
(2) ,,
.
,,
.
类型之3 矩形的性质与判定
4.(1) 证明: 四边形是平行四边形,
,
,.
为线段的中点,
,
,
,
四边形是平行四边形.
,
四边形是矩形.
(2) 解:四边形是矩形,
,.
,,
.
,
,
,
.
类型之4 菱形的性质与判定
5.(1) 证明:如答图,连接,交于点.
第5题答图
四边形是平行四边形,
.
,.
又,
,
,
四边形为平行四边形,
,.
(2) 四边形是平行四边形,
,.
,,
,
四边形是菱形,
,,
四边形是菱形.
6.(1) 证明: 四边形是平行四边形,
,.
为的中点,.
在和中,
,
.
,
四边形是平行四边形.
,为的中点,
,
四边形是菱形.
(2) 解:四边形是正方形.理由如下:
由(1)知,
,
.
又 四边形是菱形,
四边形是正方形.
类型之5 正方形的性质与判定
7.C
8.(1) 证明:过点作于点,作于点,如答图①.
第8题答图
四边形是正方形,
.
,,
,.
, ,
.
在和中,
,
, 矩形是正方形.
(2) 解:如答图②.
第8题答图
在中,,
,,
点与点重合,此时是等腰直角三角形,.
(3) 解:当 时,
.
, .
,
.
类型之6 中点四边形
9.(1) 证明:如答图,连接,交于点,交于点,交于点.
第9题答图
,,
四边形是平行四边形.
四边形是矩形, .
,分别是,的中点,
,,
.
,分别是,的中点,
,,
,,
四边形是菱形.
(2) 解:矩形的周长为22,
,.
由(1)知,四边形是菱形,
,
.
,
,,
,
,.
素养专练 培养三会
10.
11.
整合提升 练就四能
类型之1 平行四边形的性质与判定
1.[2024株洲模拟]如图,,是平行四边形对角线上的两点,.
(1) 求证:四边形是平行四边形;
(2) 若的面积为6, ,,求的长.
2.[2024长沙模拟]如图①,在中,点在的延长线上,点在的延长线上,满足.连接,分别与,相交于点,.
(1) 求证:;
(2) 如图②,连接交于点,写出图中四对全等三角形.和除外
类型之2 三角形的中位线与直角三角形斜边上的中线
3.[2024长沙模拟]如图,在中,是边上的高,是边上的中线,,是的中点.求证:
(1) ;
(2) .
类型之3 矩形的性质与判定
4.[2023大庆]如图,在中,为线段的中点,连接,,延长,与的延长线交于点,连接, .
(1) 求证:四边形是矩形;
(2) 若,,求四边形的面积.
类型之4 菱形的性质与判定
5.[2023湘西州]如图,四边形是平行四边形,,且分别交对角线于点,,连接,.
(1) 求证:;
(2) 若,求证:四边形是菱形.
6.[2024岳阳模拟]如图,在中,,分别为,的中点,,延长交的延长线于点,连接.
(1) 求证:四边形是菱形;
(2) 若 ,判断四边形的形状,并说明理由.
类型之5 正方形的性质与判定
7.[2023攀枝花]如图,已知正方形的边长为3,是对角线上的一点,于点,于点,连接.当时,( )
A. B.2 C. D.
8.如图,四边形为正方形,为线段上一点,连接,过点作,交于点,以,为邻边作矩形,连接.
(1) 求证:矩形是正方形;
(2) 若,,求的长;
(3) 当 时,求的度数.
类型之6 中点四边形
9.[2024云南]如图,在四边形中,,,,分别是各边的中点,且,,四边形是矩形.
(1) 求证:四边形是菱形;
(2) 若矩形的周长为22,四边形的面积为10,求的长.
素养专练 培养三会
10.[2023扬州]【模型观念】如图,已知正方形的边长为1,点,分别在边,上,将正方形沿着翻折,点恰好落在边上的点处.如果四边形与四边形的面积比为,那么线段的长为________.
第10题图
11.[2023广西]【模型观念】如图,在边长为2的正方形中,,分别是,上的动点,,分别是,的中点,则的最大值为______.
第11题图
本章复习课
整合提升 练就四能
类型之1 平行四边形的性质与判定
1.(1) 证明:在中,,,.
,.
在和中,
,.
又,
四边形是平行四边形.
(2) 解:如答图,过点作,交的延长线于点.
第1题答图
,,
.
, ,
.
2.(1) 证明:在中,,,
,.
在和中,
,
.
(2) 解:四对全等三角形:、、、.
类型之2 三角形的中位线与直角三角形斜边上的中线
3.(1) 证明:如答图,连接.
第3题答图
是边上的高, .
是边上的中线,即是的中点,
.
,.
又是的中点..
(2) ,,
.
,,
.
类型之3 矩形的性质与判定
4.(1) 证明: 四边形是平行四边形,
,
,.
为线段的中点,
,
,
,
四边形是平行四边形.
,
四边形是矩形.
(2) 解:四边形是矩形,
,.
,,
.
,
,
,
.
类型之4 菱形的性质与判定
5.(1) 证明:如答图,连接,交于点.
第5题答图
四边形是平行四边形,
.
,.
又,
,
,
四边形为平行四边形,
,.
(2) 四边形是平行四边形,
,.
,,
,
四边形是菱形,
,,
四边形是菱形.
6.(1) 证明: 四边形是平行四边形,
,.
为的中点,.
在和中,
,
.
,
四边形是平行四边形.
,为的中点,
,
四边形是菱形.
(2) 解:四边形是正方形.理由如下:
由(1)知,
,
.
又 四边形是菱形,
四边形是正方形.
类型之5 正方形的性质与判定
7.C
8.(1) 证明:过点作于点,作于点,如答图①.
第8题答图
四边形是正方形,
.
,,
,.
, ,
.
在和中,
,
, 矩形是正方形.
(2) 解:如答图②.
第8题答图
在中,,
,,
点与点重合,此时是等腰直角三角形,.
(3) 解:当 时,
.
, .
,
.
类型之6 中点四边形
9.(1) 证明:如答图,连接,交于点,交于点,交于点.
第9题答图
,,
四边形是平行四边形.
四边形是矩形, .
,分别是,的中点,
,,
.
,分别是,的中点,
,,
,,
四边形是菱形.
(2) 解:矩形的周长为22,
,.
由(1)知,四边形是菱形,
,
.
,
,,
,
,.
素养专练 培养三会
10.
11.
