第十八章 平行四边形 质量评估(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 第十八章 平行四边形 质量评估(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 298.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 15:57:22 | ||
图片预览



文档简介
第十八章 平行四边形 质量评估
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每题3分,共30分)
1.下列命题中,是假命题的是( )
A.菱形的面积等于两条对角线乘积的一半
B.矩形的对角线相等
C.对角线互相垂直的平行四边形是矩形
D.对角线相等的菱形是正方形
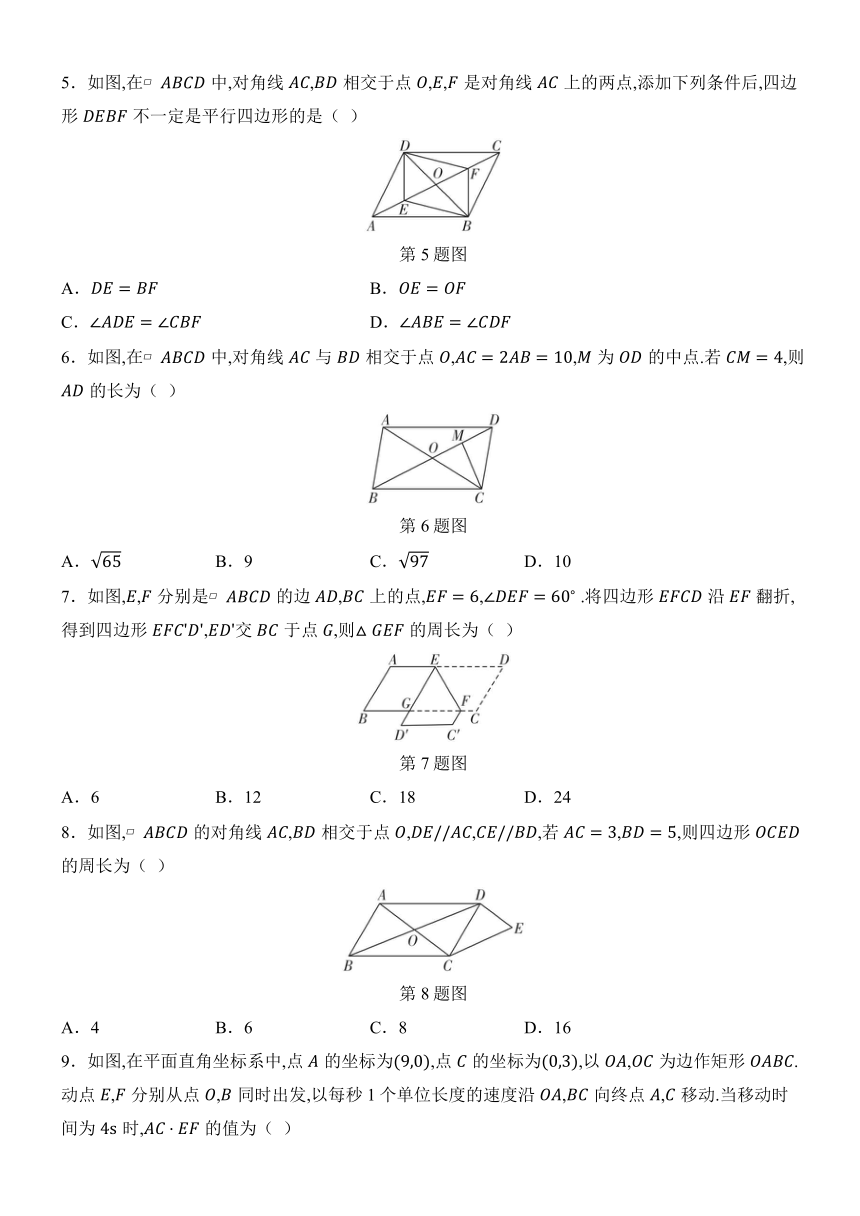
2.如图,已知四边形是平行四边形,则下列说法不正确的是( )
第2题图
A.当时,四边形是菱形
B.当时,四边形是菱形
C.当 时,四边形是矩形
D.当时,四边形是正方形
3.如图,在中,于点,且是的中点.若,,则的长为( )
第3题图
A.5 B.6 C.7 D.8
4.如图,在矩形中,对角线的垂直平分线分别交,于点,.若,,则的长为( )
第4题图
A. B.3 C. D.
5.如图,在中,对角线,相交于点,,是对角线上的两点,添加下列条件后,四边形不一定是平行四边形的是( )
第5题图
A. B.
C. D.
6.如图,在中,对角线与相交于点,,为的中点.若,则的长为( )
第6题图
A. B.9 C. D.10
7.如图,,分别是的边,上的点,, .将四边形沿翻折,得到四边形,交于点,则的周长为( )
第7题图
A.6 B.12 C.18 D.24
8.如图,的对角线,相交于点,,,若,,则四边形的周长为( )
第8题图
A.4 B.6 C.8 D.16
9.如图,在平面直角坐标系中,点的坐标为,点的坐标为,以,为边作矩形.动点,分别从点,同时出发,以每秒1个单位长度的速度沿,向终点,移动.当移动时间为时,的值为( )
第9题图
A. B. C.15 D.30
10.如图,的面积为12,,与相交于点,分别过点,作,的平行线,相交于点,是的中点,是四边形边上的动点,则的最小值是( )
第10题图
A.1 B. C. D.3
二、填空题(共6个小题,每题3分,共18分)
11.如图,在菱形中,,,则菱形的面积是__.
第11题图
12.如图,在中,,是对角线上两点,, , ,则的度数为________.
第12题图
13.如图,点,在菱形的对角线上,, , ,则的度数是________.
第13题图
14.如图,在正方形中,对角线与相交于点,为上一点,,为的中点.若的周长为32,则的长为________.
第14题图
15.如图,在矩形中,于点.若,则________.
第15题图
16.如图,在矩形中,,,点在边上,且,,分别是边,上的动点,且,是线段上的动点,连接,.若,则线段的长为________.
第16题图
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,在中,平分交于点,交于点,平分交于点.求证:.
18.(6分)如图,在菱形中,,垂足为,,垂足为.求证:.
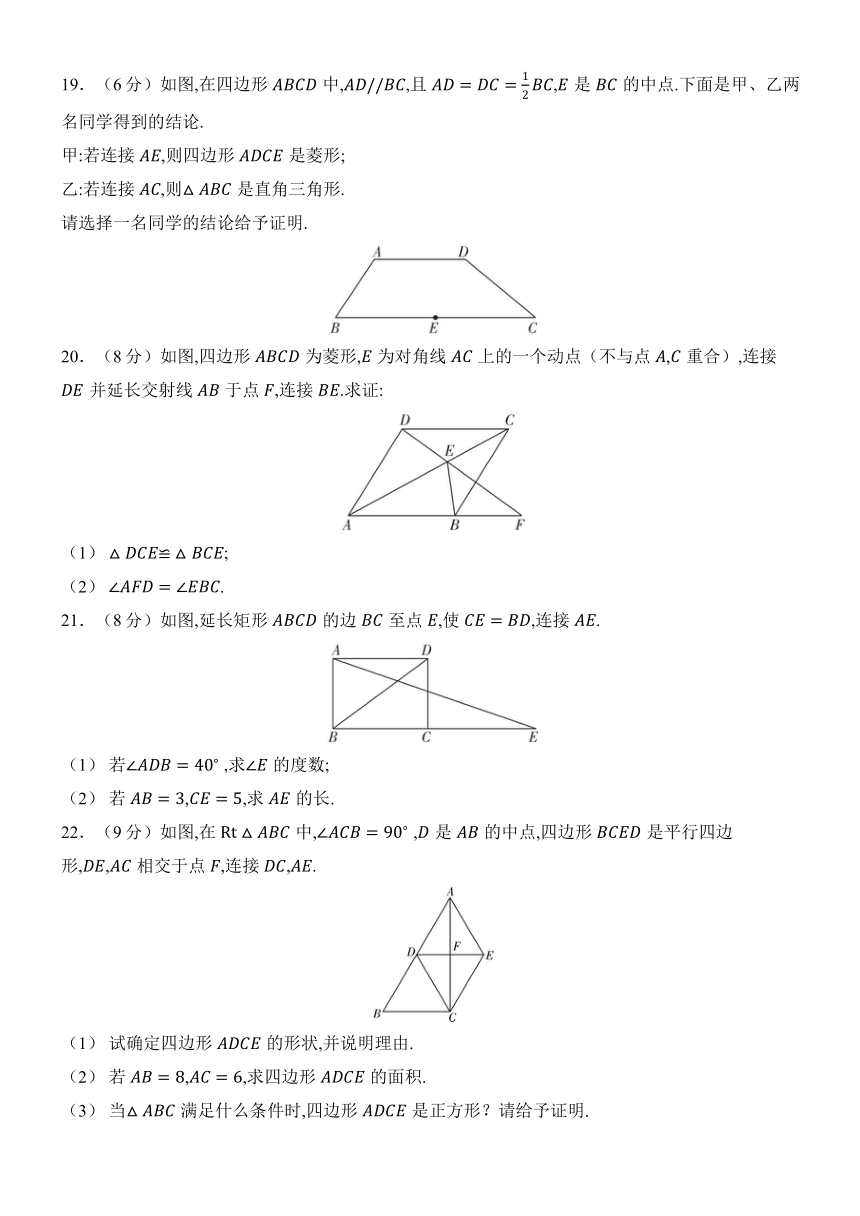
19.(6分)如图,在四边形中,,且,是的中点.下面是甲、乙两名同学得到的结论.
甲:若连接,则四边形是菱形;
乙:若连接,则是直角三角形.
请选择一名同学的结论给予证明.
20.(8分)如图,四边形为菱形,为对角线上的一个动点(不与点,重合),连接并延长交射线于点,连接.求证:
(1) ;
(2) .
21.(8分)如图,延长矩形的边至点,使,连接.
(1) 若 ,求的度数;
(2) 若,,求的长.
22.(9分)如图,在中, ,是的中点,四边形是平行四边形,,相交于点,连接,.
(1) 试确定四边形的形状,并说明理由.
(2) 若,,求四边形的面积.
(3) 当满足什么条件时,四边形是正方形?请给予证明.
23.(9分)如图,在中, ,于点,平分,交于点,交于点,于点.求证:四边形是菱形.
24.(10分)如图,在菱形中,对角线,相交于点,过点作于点,延长至点,使,连接.
(1) 求证:四边形是矩形;
(2) 若,,求的长.
25.(10分)“先天下之忧而忧,后天下之乐而乐”这是《岳阳楼记》中的一句千古名言,也是岳阳精神的真实写照,这句话具有鲜明的对称美.如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图①,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”.
(1) 下列四边形一定是“忧乐四边形”的有__(填写序号).
①平行四边形;②矩形;③正方形;④菱形;⑤梯形.
(2) 在四边形中,是边上的中点,四边形是以直线为对称轴的“忧乐四边形”(点在四边形内部),连接并延长交于点.
① 如图②,若四边形是矩形,求证:四边形是“忧乐四边形”;
② 如图③,若四边形是平行四边形,①中的结论是否仍然成立 请说明理由.
第十八章质量评估
一、选择题(共10个小题,每题3分,共30分)
1.C 2.D 3.D 4.A 5.A 6.C 7.C 8.C 9.D 10.A
二、填空题(共6个小题,每题3分,共18分)
11.24
12.
13.
14.
15.
16.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.证明: 四边形是平行四边形,
,,,
.
平分,平分,
,,
.
在和中,
,
.
18.证明: 四边形是菱形,
.
,,
.
在和中,
,
,
,
.
19.证明:选择甲,连接,如答图①,
第19题答图①
是的中点,,
,,
, 四边形是平行四边形.
, 四边形是菱形.
选择乙,如答图②,连接,,,交于点.
第19题答图②
,是的中点,.
,
四边形是平行四边形,四边形是平行四边形.
, 四边形是菱形,
, .
四边形是平行四边形,,
,是直角三角形.
20.(1) 证明: 四边形是菱形,
,.
在和中,
.
(2) ,
.
四边形是菱形,,
,
.
21.(1) 解:连接,交于点,如答图.
第21题答图
四边形是矩形,,
,,
,.
,,
,即 .
.
.
(2) ,,.
.
.
22.(1) 解:四边形是菱形.理由如下:
四边形是平行四边形,
,,.
为的中点,,
,,
四边形是平行四边形.
又, ,
, 四边形是菱形.
(2) 在中,
,,.
由(1)知,四边形是菱形,,
.
(3) 当满足时,四边形是正方形.
证明:,为的中点,
,即 .
又由(1)知四边形是菱形.
菱形是正方形.
23.证明:如答图,
第23题答图
, ,,平分,
,,.
,,.
,,,.
.
, 四边形是平行四边形.
又, 四边形是菱形.
24.(1) 证明: 四边形是菱形,,.
,,
,.
, 四边形是平行四边形.
,
四边形是矩形.
(2) 解:四边形是菱形,.
,.
在矩形中, ,,
在中,,
解得.
的长为10.
25.(1) ③④
(2) ① 证明:如答图①,连接.
第25题答图
四边形是矩形, .
是的中点,.
将沿折叠后得到,
,,.
.
在和中,
,
四边形沿折叠完全重合,
四边形是“忧乐四边形”.
② 解:①中的结论仍然成立.理由如下:
如答图②,连接,.
是的中点,.
将沿折叠后得到,
,,,.
四边形是平行四边形,
,,
且,
,
,
,.
在和中,
,
四边形沿折叠完全重合,
四边形是“忧乐四边形”.
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每题3分,共30分)
1.下列命题中,是假命题的是( )
A.菱形的面积等于两条对角线乘积的一半
B.矩形的对角线相等
C.对角线互相垂直的平行四边形是矩形
D.对角线相等的菱形是正方形
2.如图,已知四边形是平行四边形,则下列说法不正确的是( )
第2题图
A.当时,四边形是菱形
B.当时,四边形是菱形
C.当 时,四边形是矩形
D.当时,四边形是正方形
3.如图,在中,于点,且是的中点.若,,则的长为( )
第3题图
A.5 B.6 C.7 D.8
4.如图,在矩形中,对角线的垂直平分线分别交,于点,.若,,则的长为( )
第4题图
A. B.3 C. D.
5.如图,在中,对角线,相交于点,,是对角线上的两点,添加下列条件后,四边形不一定是平行四边形的是( )
第5题图
A. B.
C. D.
6.如图,在中,对角线与相交于点,,为的中点.若,则的长为( )
第6题图
A. B.9 C. D.10
7.如图,,分别是的边,上的点,, .将四边形沿翻折,得到四边形,交于点,则的周长为( )
第7题图
A.6 B.12 C.18 D.24
8.如图,的对角线,相交于点,,,若,,则四边形的周长为( )
第8题图
A.4 B.6 C.8 D.16
9.如图,在平面直角坐标系中,点的坐标为,点的坐标为,以,为边作矩形.动点,分别从点,同时出发,以每秒1个单位长度的速度沿,向终点,移动.当移动时间为时,的值为( )
第9题图
A. B. C.15 D.30
10.如图,的面积为12,,与相交于点,分别过点,作,的平行线,相交于点,是的中点,是四边形边上的动点,则的最小值是( )
第10题图
A.1 B. C. D.3
二、填空题(共6个小题,每题3分,共18分)
11.如图,在菱形中,,,则菱形的面积是__.
第11题图
12.如图,在中,,是对角线上两点,, , ,则的度数为________.
第12题图
13.如图,点,在菱形的对角线上,, , ,则的度数是________.
第13题图
14.如图,在正方形中,对角线与相交于点,为上一点,,为的中点.若的周长为32,则的长为________.
第14题图
15.如图,在矩形中,于点.若,则________.
第15题图
16.如图,在矩形中,,,点在边上,且,,分别是边,上的动点,且,是线段上的动点,连接,.若,则线段的长为________.
第16题图
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,在中,平分交于点,交于点,平分交于点.求证:.
18.(6分)如图,在菱形中,,垂足为,,垂足为.求证:.
19.(6分)如图,在四边形中,,且,是的中点.下面是甲、乙两名同学得到的结论.
甲:若连接,则四边形是菱形;
乙:若连接,则是直角三角形.
请选择一名同学的结论给予证明.
20.(8分)如图,四边形为菱形,为对角线上的一个动点(不与点,重合),连接并延长交射线于点,连接.求证:
(1) ;
(2) .
21.(8分)如图,延长矩形的边至点,使,连接.
(1) 若 ,求的度数;
(2) 若,,求的长.
22.(9分)如图,在中, ,是的中点,四边形是平行四边形,,相交于点,连接,.
(1) 试确定四边形的形状,并说明理由.
(2) 若,,求四边形的面积.
(3) 当满足什么条件时,四边形是正方形?请给予证明.
23.(9分)如图,在中, ,于点,平分,交于点,交于点,于点.求证:四边形是菱形.
24.(10分)如图,在菱形中,对角线,相交于点,过点作于点,延长至点,使,连接.
(1) 求证:四边形是矩形;
(2) 若,,求的长.
25.(10分)“先天下之忧而忧,后天下之乐而乐”这是《岳阳楼记》中的一句千古名言,也是岳阳精神的真实写照,这句话具有鲜明的对称美.如果一个凸四边形沿着它的一条对角线对折后能完全重合,我们就把这个四边形称为“忧乐四边形”.如图①,凸四边形沿对角线对折后完全重合,四边形是以直线为对称轴的“忧乐四边形”.
(1) 下列四边形一定是“忧乐四边形”的有__(填写序号).
①平行四边形;②矩形;③正方形;④菱形;⑤梯形.
(2) 在四边形中,是边上的中点,四边形是以直线为对称轴的“忧乐四边形”(点在四边形内部),连接并延长交于点.
① 如图②,若四边形是矩形,求证:四边形是“忧乐四边形”;
② 如图③,若四边形是平行四边形,①中的结论是否仍然成立 请说明理由.
第十八章质量评估
一、选择题(共10个小题,每题3分,共30分)
1.C 2.D 3.D 4.A 5.A 6.C 7.C 8.C 9.D 10.A
二、填空题(共6个小题,每题3分,共18分)
11.24
12.
13.
14.
15.
16.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.证明: 四边形是平行四边形,
,,,
.
平分,平分,
,,
.
在和中,
,
.
18.证明: 四边形是菱形,
.
,,
.
在和中,
,
,
,
.
19.证明:选择甲,连接,如答图①,
第19题答图①
是的中点,,
,,
, 四边形是平行四边形.
, 四边形是菱形.
选择乙,如答图②,连接,,,交于点.
第19题答图②
,是的中点,.
,
四边形是平行四边形,四边形是平行四边形.
, 四边形是菱形,
, .
四边形是平行四边形,,
,是直角三角形.
20.(1) 证明: 四边形是菱形,
,.
在和中,
.
(2) ,
.
四边形是菱形,,
,
.
21.(1) 解:连接,交于点,如答图.
第21题答图
四边形是矩形,,
,,
,.
,,
,即 .
.
.
(2) ,,.
.
.
22.(1) 解:四边形是菱形.理由如下:
四边形是平行四边形,
,,.
为的中点,,
,,
四边形是平行四边形.
又, ,
, 四边形是菱形.
(2) 在中,
,,.
由(1)知,四边形是菱形,,
.
(3) 当满足时,四边形是正方形.
证明:,为的中点,
,即 .
又由(1)知四边形是菱形.
菱形是正方形.
23.证明:如答图,
第23题答图
, ,,平分,
,,.
,,.
,,,.
.
, 四边形是平行四边形.
又, 四边形是菱形.
24.(1) 证明: 四边形是菱形,,.
,,
,.
, 四边形是平行四边形.
,
四边形是矩形.
(2) 解:四边形是菱形,.
,.
在矩形中, ,,
在中,,
解得.
的长为10.
25.(1) ③④
(2) ① 证明:如答图①,连接.
第25题答图
四边形是矩形, .
是的中点,.
将沿折叠后得到,
,,.
.
在和中,
,
四边形沿折叠完全重合,
四边形是“忧乐四边形”.
② 解:①中的结论仍然成立.理由如下:
如答图②,连接,.
是的中点,.
将沿折叠后得到,
,,,.
四边形是平行四边形,
,,
且,
,
,
,.
在和中,
,
四边形沿折叠完全重合,
四边形是“忧乐四边形”.
