第十九章 一次函数 质量评估(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 第十九章 一次函数 质量评估(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 16:00:00 | ||
图片预览




文档简介
第十九章 一次函数 质量评估
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每题3分,共30分)
1.若点在一次函数的图象上,则点一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
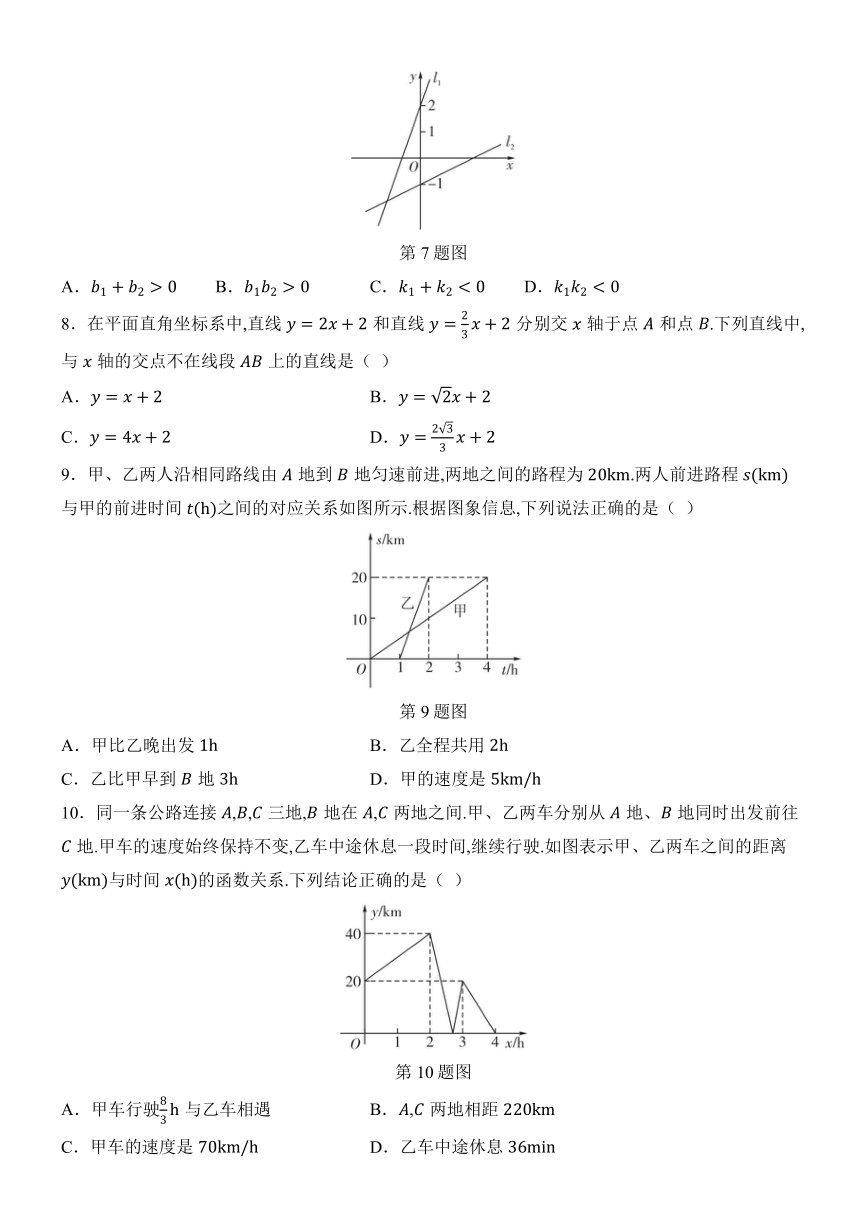
2.如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数与铁块被提起的时间之间的函数关系的大致图象是( )
A.
B.
C.
D.
3.已知将直线向上平移2个单位长度后得到直线,则下列关于直线的说法正确的是( )
A.经过第一、二、四象限 B.与轴交于点
C.与轴交于点 D.随的增大而减小
4.已知一次函数,为常数,的图象经过第一、三、四象限,则下列结论一定正确的是( )
A. B. C. D.
5.在同一平面直角坐标系中,直线与相交于点,则关于,的方程组的解为( )
A. B.
C. D.
6.如图,一次函数和的图象相交于点,则不等式的解集是( )
第6题图
A. B. C. D.
7.如图,在同一平面直角坐标系中,一次函数与(其中,,,,为常数)的图象分别为直线,.下列结论正确的是( )
第7题图
A. B. C. D.
8.在平面直角坐标系中,直线和直线分别交轴于点和点.下列直线中,与轴的交点不在线段上的直线是( )
A. B.
C. D.
9.甲、乙两人沿相同路线由地到地匀速前进,两地之间的路程为.两人前进路程与甲的前进时间之间的对应关系如图所示.根据图象信息,下列说法正确的是( )
第9题图
A.甲比乙晚出发 B.乙全程共用
C.乙比甲早到地 D.甲的速度是
10.同一条公路连接,,三地,地在,两地之间.甲、乙两车分别从地、地同时出发前往地.甲车的速度始终保持不变,乙车中途休息一段时间,继续行驶.如图表示甲、乙两车之间的距离与时间的函数关系.下列结论正确的是( )
第10题图
A.甲车行驶与乙车相遇 B.,两地相距
C.甲车的速度是 D.乙车中途休息
二、填空题(共6个小题,每题3分,共18分)
11.在平面直角坐标系中,一条直线与两坐标轴围成的三角形是等腰三角形,则该直线的解析式可能为____________________________(写出一个即可).
12.一次函数的图象经过点.当时,的取值范围是________.
13.若点关于轴的对称点在第四象限内,则一次函数的图象不经过第__象限.
14.如图,函数的图象经过点,则关于的不等式的解集为____________.
第14题图
15.小王前往距家的公司参会,先以的速度步行一段时间后,再改骑共享单车直达会议地点,到达时距会议开始还有,小王距家的路程与离家的时间之间的函数图象如图所示.若小王全程以的速度步行,则他到达时距会议开始还有____.
第15题图
16.在平面直角坐标系中,已知,,直线,为常数,且经过点,并把分成两部分,其中靠近原点部分的面积为,则的值为________.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,已知一次函数的图象经过,两点.
(1) 求一次函数的解析式;
(2) 若为轴上一点,且的面积为6,求点的坐标.
18.(6分)在所给的平面直角坐标系中,作出函数的图象,并解答下列问题:
(1) 函数图象与轴、轴分别交于点,,则点的坐标为____________,点的坐标为____________;
(2) 求原点到此函数图象的距离.
19.(6分)如图,一次函数的图象与轴交于点,与过点的一次函数的图象交于点.求:
(1) 的值;
(2) 一次函数图象对应的函数解析式;
(3) 的面积.
20.(8分)某通信公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为元,B套餐每月话费为元,月通话时间为.
(1) 分别表示出,与的函数关系式.
(2) 什么情况下A套餐更省钱?
21.(8分)绍兴首条智慧快速路于2023年3月19日正式通车,该快速路上,两站相距,甲、乙两名杭州亚运会会务工作志愿者从站出发前往站附近的比赛场馆开展服务,甲乘坐无人驾驶小巴,乙乘坐无人驾驶汽车,甲比乙提前出发,图中,分别表示甲、乙离开站的路程与甲出发的时间的函数关系的图象.根据图象解答下列问题:
(1) 求乙离开站的路程关于甲出发的时间的函数解析式;
(2) 在两车都行驶的过程中,当汽车与小巴相距时,求的值.
22.(9分)端午节期间,小明一家自驾游去了离家的某地,如图是他们离家的距离与汽车行驶时间的函数图象,根据图象解答下列问题:
(1) 求出线段的函数解析式;
(2) 求当他们离家时,共用了多少小时?(提示:图中的,,均为线段)
23.(9分)某班同学分三个小组进行“板凳中的数学”的项目式学习研究.第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为,凳面的宽度为,记录如下表:
以对称轴为基准向两边各取相同的长度 16.5 19.8 23.1 26.4 29.7
凳面的宽度 115.5 132 148.5 165 181.5
【分析数据】
如图③,小组根据表中,的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1) 观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,请求出这条直线所对应的函数解析式;如果不在同一条直线上,请说明理由.
(2) 当凳面宽度为时,以对称轴为基准向两边各取相同的长度是多少?
24.(10分)根据如表所示素材,探索完成任务.
如何确定图书销售单价及怎样进货以获取最大利润
素材一 某书店决定购进A,B两种新书,两种图书的进价分别是每本18元、每本12元.
素材二 已知A种图书的标价是B种图书标价的1.5倍,若顾客用540元按标价购买图书,能单独购买A种图书的数量恰好比单独购买B种图书的数量少10本.
素材三 书店准备用不超过1 680元购进A,B两种图书共100本,且A种图书不少于70本,经市场调查后调整销售方案为:A种图书按照标价的八折销售,B种图书按标价销售.
问题解决
任务一 探求图书的标价 (1)请运用适当方法,求出A,B两种图书的标价.
任务二 如何获得最大利润 (2)书店应怎样进货才能获得最大利润?
25.(10分)如图,如果两个一次函数和的图象关于直线对称,那么称这两个一次函数为“守望函数”.由轴对称知识可知这两条直线的交点必定在直线上,我们称这个交点为“守望点”,两条直线与坐标轴的交点分别为,.同样由轴对称知识可知.
(1) 已知函数与为“守望函数”,求“守望点”的坐标及的值;
(2) 在(1)条件下,若平面内有一点,使得,,,四个点构成的四边形是平行四边形,请求出满足条件的所有点的坐标.
第十九章质量评估
一、选择题(共10个小题,每题3分,共30分)
1.C 2.A 3.C 4.B 5.C 6.C 7.A 8.C 9.D 10.A
二、填空题(共6个小题,每题3分,共18分)
11.(答案不唯一)
12.
13.一
14.
15.5
16.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(1) 解:设一次函数的解析式为.
把点,的坐标分别代入,得
解得
一次函数的解析式为.
(2) 设点的坐标为.
的面积为6,
,即,
解得或,
或.
18.(1) 解:函数的图象如答图所示.
第18题答图
18.(1) ;
(2) 根据,可知,,
在中,.
设原点到函数的距离为,
,
,解得.
原点到此函数图象的距离为.
19.(1) 解: 点在一次函数的图象上,
.
(2) 设一次函数图象对应的函数解析式为.
把点,的坐标分别代入,得解得
一次函数图象对应的函数解析式为.
(3) 一次函数的图象与轴交于点,.
,,,
.
20.(1) 解:由题意,可得,.
(2) 由题意,可得,
解得.
答:当月通话时间多于时,A套餐更省钱.
21.(1) 解:设乙离开站的路程关于甲出发的时间的函数解析式为.
把和的坐标分别代入,得解得
.
(2) 由图可得甲离开站的路程关于甲出发的时间的函数解析式为.
由题意,得,
或,
解得或.
的值为13或7.
22.(1) 解:设线段的函数解析式为.
将的坐标代入,得.
.
(2) 设线段的函数解析式为.
将,的坐标分别代入,得
解得
.
当时,,
解得.
答:当他们离家时,共用了.
23.(1) 解:它们在同一条直线上.设这条直线所对应的函数解析式是.将,的坐标分别代入,得解得
这条直线所对应的函数解析式为.
(2) 当时,,解得.
当凳面宽度为时,以对称轴为基准向两边各取相同的长度是.
24.(1)解:设B种图书的标价是元,则A种图书的标价是元.
由题意,得,
解得,经检验,是原方程的解,且符合题意,
此时.
答:A种图书的标价是27元,B种图书的标价是18元.
(2)设购进A种图书本,则购进B种图书本.
由题意,得,.
又,,且为整数.
设获得的总利润为元,则
.
,
随的减小而增大.
,且为整数,
当时,取最大值,此时购进B种图书(本).
答:书店购进A种图书70本、B种图书30本才能获得最大利润.
25.(1) 解:设“守望函数”与的“守望点”,
解得
“守望点”的坐标为,的值为.
(2) 设.
函数与轴交点的坐标为,函数与轴交点的坐标为,.
①若,为对角线,则,的中点重合,则
解得
;
②若,为对角线,则,的中点重合,则
解得;
③若,为对角线,则,的中点重合,则
解得.
综上所述,点的坐标为,或.
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每题3分,共30分)
1.若点在一次函数的图象上,则点一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,用弹簧测力计将一铁块悬于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度,则下列能反映弹簧测力计的读数与铁块被提起的时间之间的函数关系的大致图象是( )
A.
B.
C.
D.
3.已知将直线向上平移2个单位长度后得到直线,则下列关于直线的说法正确的是( )
A.经过第一、二、四象限 B.与轴交于点
C.与轴交于点 D.随的增大而减小
4.已知一次函数,为常数,的图象经过第一、三、四象限,则下列结论一定正确的是( )
A. B. C. D.
5.在同一平面直角坐标系中,直线与相交于点,则关于,的方程组的解为( )
A. B.
C. D.
6.如图,一次函数和的图象相交于点,则不等式的解集是( )
第6题图
A. B. C. D.
7.如图,在同一平面直角坐标系中,一次函数与(其中,,,,为常数)的图象分别为直线,.下列结论正确的是( )
第7题图
A. B. C. D.
8.在平面直角坐标系中,直线和直线分别交轴于点和点.下列直线中,与轴的交点不在线段上的直线是( )
A. B.
C. D.
9.甲、乙两人沿相同路线由地到地匀速前进,两地之间的路程为.两人前进路程与甲的前进时间之间的对应关系如图所示.根据图象信息,下列说法正确的是( )
第9题图
A.甲比乙晚出发 B.乙全程共用
C.乙比甲早到地 D.甲的速度是
10.同一条公路连接,,三地,地在,两地之间.甲、乙两车分别从地、地同时出发前往地.甲车的速度始终保持不变,乙车中途休息一段时间,继续行驶.如图表示甲、乙两车之间的距离与时间的函数关系.下列结论正确的是( )
第10题图
A.甲车行驶与乙车相遇 B.,两地相距
C.甲车的速度是 D.乙车中途休息
二、填空题(共6个小题,每题3分,共18分)
11.在平面直角坐标系中,一条直线与两坐标轴围成的三角形是等腰三角形,则该直线的解析式可能为____________________________(写出一个即可).
12.一次函数的图象经过点.当时,的取值范围是________.
13.若点关于轴的对称点在第四象限内,则一次函数的图象不经过第__象限.
14.如图,函数的图象经过点,则关于的不等式的解集为____________.
第14题图
15.小王前往距家的公司参会,先以的速度步行一段时间后,再改骑共享单车直达会议地点,到达时距会议开始还有,小王距家的路程与离家的时间之间的函数图象如图所示.若小王全程以的速度步行,则他到达时距会议开始还有____.
第15题图
16.在平面直角坐标系中,已知,,直线,为常数,且经过点,并把分成两部分,其中靠近原点部分的面积为,则的值为________.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)如图,已知一次函数的图象经过,两点.
(1) 求一次函数的解析式;
(2) 若为轴上一点,且的面积为6,求点的坐标.
18.(6分)在所给的平面直角坐标系中,作出函数的图象,并解答下列问题:
(1) 函数图象与轴、轴分别交于点,,则点的坐标为____________,点的坐标为____________;
(2) 求原点到此函数图象的距离.
19.(6分)如图,一次函数的图象与轴交于点,与过点的一次函数的图象交于点.求:
(1) 的值;
(2) 一次函数图象对应的函数解析式;
(3) 的面积.
20.(8分)某通信公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种.设A套餐每月话费为元,B套餐每月话费为元,月通话时间为.
(1) 分别表示出,与的函数关系式.
(2) 什么情况下A套餐更省钱?
21.(8分)绍兴首条智慧快速路于2023年3月19日正式通车,该快速路上,两站相距,甲、乙两名杭州亚运会会务工作志愿者从站出发前往站附近的比赛场馆开展服务,甲乘坐无人驾驶小巴,乙乘坐无人驾驶汽车,甲比乙提前出发,图中,分别表示甲、乙离开站的路程与甲出发的时间的函数关系的图象.根据图象解答下列问题:
(1) 求乙离开站的路程关于甲出发的时间的函数解析式;
(2) 在两车都行驶的过程中,当汽车与小巴相距时,求的值.
22.(9分)端午节期间,小明一家自驾游去了离家的某地,如图是他们离家的距离与汽车行驶时间的函数图象,根据图象解答下列问题:
(1) 求出线段的函数解析式;
(2) 求当他们离家时,共用了多少小时?(提示:图中的,,均为线段)
23.(9分)某班同学分三个小组进行“板凳中的数学”的项目式学习研究.第一小组负责调查板凳的历史及结构特点;第二小组负责研究板凳中蕴含的数学知识;第三小组负责汇报和交流.下面是第三小组汇报的部分内容,请你阅读相关信息,并解答“建立模型”中的问题.
【背景调查】
图①中的板凳又叫“四脚八叉凳”,是中国传统家具,其榫卯结构体现了古人含蓄内敛的审美观.榫眼的设计很有讲究,木工一般用铅笔画出凳面的对称轴,以对称轴为基准向两边各取相同的长度,确定榫眼的位置,如图②所示.板凳的结构设计体现了数学的对称美.
【收集数据】
小组收集了一些板凳并进行了测量.设以对称轴为基准向两边各取相同的长度为,凳面的宽度为,记录如下表:
以对称轴为基准向两边各取相同的长度 16.5 19.8 23.1 26.4 29.7
凳面的宽度 115.5 132 148.5 165 181.5
【分析数据】
如图③,小组根据表中,的数值,在平面直角坐标系中描出了各点.
【建立模型】
请你帮助小组解决下列问题:
(1) 观察上述各点的分布规律,它们是否在同一条直线上?如果在同一条直线上,请求出这条直线所对应的函数解析式;如果不在同一条直线上,请说明理由.
(2) 当凳面宽度为时,以对称轴为基准向两边各取相同的长度是多少?
24.(10分)根据如表所示素材,探索完成任务.
如何确定图书销售单价及怎样进货以获取最大利润
素材一 某书店决定购进A,B两种新书,两种图书的进价分别是每本18元、每本12元.
素材二 已知A种图书的标价是B种图书标价的1.5倍,若顾客用540元按标价购买图书,能单独购买A种图书的数量恰好比单独购买B种图书的数量少10本.
素材三 书店准备用不超过1 680元购进A,B两种图书共100本,且A种图书不少于70本,经市场调查后调整销售方案为:A种图书按照标价的八折销售,B种图书按标价销售.
问题解决
任务一 探求图书的标价 (1)请运用适当方法,求出A,B两种图书的标价.
任务二 如何获得最大利润 (2)书店应怎样进货才能获得最大利润?
25.(10分)如图,如果两个一次函数和的图象关于直线对称,那么称这两个一次函数为“守望函数”.由轴对称知识可知这两条直线的交点必定在直线上,我们称这个交点为“守望点”,两条直线与坐标轴的交点分别为,.同样由轴对称知识可知.
(1) 已知函数与为“守望函数”,求“守望点”的坐标及的值;
(2) 在(1)条件下,若平面内有一点,使得,,,四个点构成的四边形是平行四边形,请求出满足条件的所有点的坐标.
第十九章质量评估
一、选择题(共10个小题,每题3分,共30分)
1.C 2.A 3.C 4.B 5.C 6.C 7.A 8.C 9.D 10.A
二、填空题(共6个小题,每题3分,共18分)
11.(答案不唯一)
12.
13.一
14.
15.5
16.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(1) 解:设一次函数的解析式为.
把点,的坐标分别代入,得
解得
一次函数的解析式为.
(2) 设点的坐标为.
的面积为6,
,即,
解得或,
或.
18.(1) 解:函数的图象如答图所示.
第18题答图
18.(1) ;
(2) 根据,可知,,
在中,.
设原点到函数的距离为,
,
,解得.
原点到此函数图象的距离为.
19.(1) 解: 点在一次函数的图象上,
.
(2) 设一次函数图象对应的函数解析式为.
把点,的坐标分别代入,得解得
一次函数图象对应的函数解析式为.
(3) 一次函数的图象与轴交于点,.
,,,
.
20.(1) 解:由题意,可得,.
(2) 由题意,可得,
解得.
答:当月通话时间多于时,A套餐更省钱.
21.(1) 解:设乙离开站的路程关于甲出发的时间的函数解析式为.
把和的坐标分别代入,得解得
.
(2) 由图可得甲离开站的路程关于甲出发的时间的函数解析式为.
由题意,得,
或,
解得或.
的值为13或7.
22.(1) 解:设线段的函数解析式为.
将的坐标代入,得.
.
(2) 设线段的函数解析式为.
将,的坐标分别代入,得
解得
.
当时,,
解得.
答:当他们离家时,共用了.
23.(1) 解:它们在同一条直线上.设这条直线所对应的函数解析式是.将,的坐标分别代入,得解得
这条直线所对应的函数解析式为.
(2) 当时,,解得.
当凳面宽度为时,以对称轴为基准向两边各取相同的长度是.
24.(1)解:设B种图书的标价是元,则A种图书的标价是元.
由题意,得,
解得,经检验,是原方程的解,且符合题意,
此时.
答:A种图书的标价是27元,B种图书的标价是18元.
(2)设购进A种图书本,则购进B种图书本.
由题意,得,.
又,,且为整数.
设获得的总利润为元,则
.
,
随的减小而增大.
,且为整数,
当时,取最大值,此时购进B种图书(本).
答:书店购进A种图书70本、B种图书30本才能获得最大利润.
25.(1) 解:设“守望函数”与的“守望点”,
解得
“守望点”的坐标为,的值为.
(2) 设.
函数与轴交点的坐标为,函数与轴交点的坐标为,.
①若,为对角线,则,的中点重合,则
解得
;
②若,为对角线,则,的中点重合,则
解得;
③若,为对角线,则,的中点重合,则
解得.
综上所述,点的坐标为,或.
