第十七章 勾股定理 质量评估(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 第十七章 勾股定理 质量评估(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 245.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 16:01:55 | ||
图片预览



文档简介
第十七章 勾股定理 质量评估
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每题3分,共30分)
1.在中,斜边,则( )
A.20 B.100 C.200 D.144
2.满足下述条件的三角形中,不是直角三角形的是( )
A.三个内角度数之比为 B.三条边长之比为
C.三条边长分别为41,40,9 D.三条边长分别为,,8
3.若一个三角形三边,,满足,则这个三角形是( )
A.等边三角形 B.钝角三角形
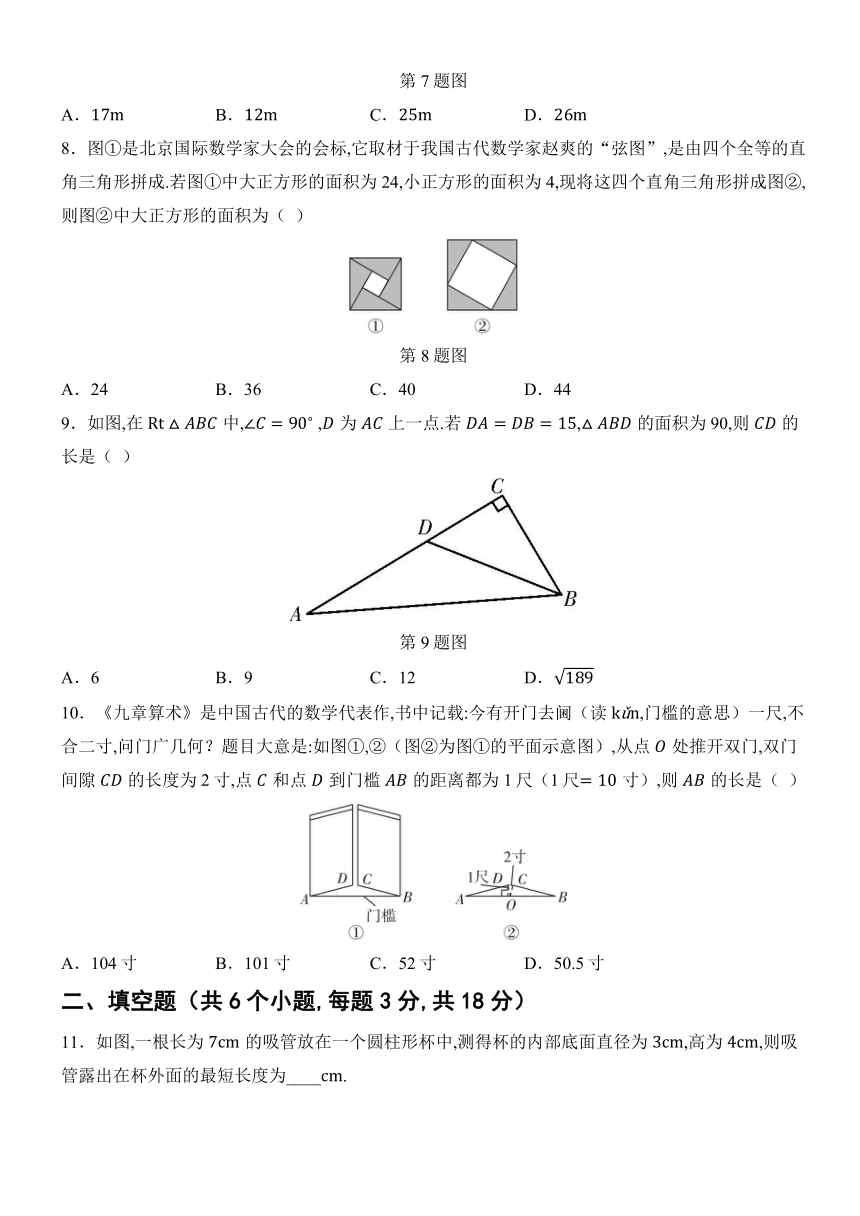
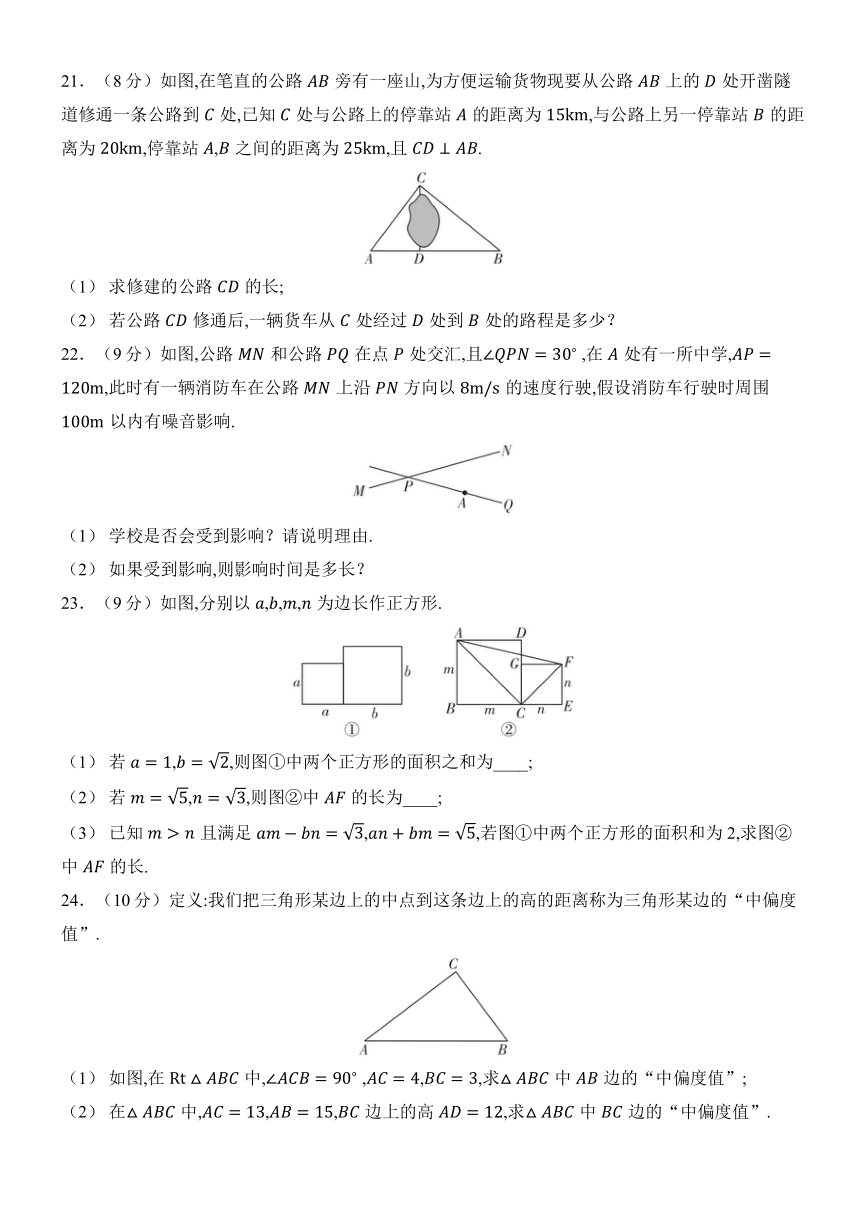
C.等腰直角三角形 D.直角三角形
4.人在平地上以的速度向西走了,接着以的速度向南走了,这时他距离出发点( )
A. B. C. D.
5.如图,所有阴影四边形都是正方形,所有三角形都是直角三角形.已知正方形,,的面积依次为2,4,3,则正方形的面积为( )
第5题图
A.9 B.8 C.27 D.45
6.如图,是等边三角形,边长为2,根据作图的痕迹,则的长为( )
第6题图
A.1.7 B. C. D.
7.如图,在高为,坡面长为的楼梯表面铺地毯,地毯的长度至少需要( )
第7题图
A. B. C. D.
8.图①是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图①中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图②,则图②中大正方形的面积为( )
第8题图
A.24 B.36 C.40 D.44
9.如图,在中, ,为上一点.若,的面积为90,则的长是( )
第9题图
A.6 B.9 C.12 D.
10.《九章算术》是中国古代的数学代表作,书中记载:今有开门去阃(读,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①,②(图②为图①的平面示意图),从点处推开双门,双门间隙的长度为2寸,点和点到门槛的距离都为1尺(1尺寸),则的长是( )
A.104寸 B.101寸 C.52寸 D.50.5寸
二、填空题(共6个小题,每题3分,共18分)
11.如图,一根长为的吸管放在一个圆柱形杯中,测得杯的内部底面直径为,高为,则吸管露出在杯外面的最短长度为____.
第11题图
12.如图,在一根长的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为____.
第12题图
13.将折叠书架画出侧面示意图,为面板架,为支撑架,为锁定杆,可在上移动或固定.已知.如图①,将面板竖直固定时,恰为的中点.如图②,当时,,则支撑架的长度为________.
14.如图,在中, ,,,为上一点.若是的平分线,则____.
第14题图
15.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从处先往东走,又往北走,遇到障碍后又往西走,再转向北走往东拐,仅走就到达了处.,两点之间的距离为__.
第15题图
16.如图,长方体的长、宽、高分别是,,,一只蚂蚁沿着长方体的表面从点爬到点,则蚂蚁爬行的最短路径长为________.
第16题图
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)已知:在中, ,,,.
(1) 若,,求的值;
(2) 若,,求的值.
18.(6分)如图,是平面直角坐标系中的一点.
(1) 用二次根式表示线段的长;
(2) 若,,求的长.
19.(6分)如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行,“海天”号每小时航行.它们离开港口后分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,那么能知道“海天”号沿哪个方向航行吗?
20.(8分)11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题,小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺,两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以同样的速度飞去抓鱼,并且同时到达目标.这条鱼出现的地方离较高的棕榈树的树根有多远?
21.(8分)如图,在笔直的公路旁有一座山,为方便运输货物现要从公路上的处开凿隧道修通一条公路到处,已知处与公路上的停靠站的距离为,与公路上另一停靠站的距离为,停靠站,之间的距离为,且.
(1) 求修建的公路的长;
(2) 若公路修通后,一辆货车从处经过处到处的路程是多少?
22.(9分)如图,公路和公路在点处交汇,且 ,在处有一所中学,,此时有一辆消防车在公路上沿方向以的速度行驶,假设消防车行驶时周围以内有噪音影响.
(1) 学校是否会受到影响?请说明理由.
(2) 如果受到影响,则影响时间是多长?
23.(9分)如图,分别以,,,为边长作正方形.
(1) 若,,则图①中两个正方形的面积之和为____;
(2) 若,,则图②中的长为____;
(3) 已知且满足,,若图①中两个正方形的面积和为2,求图②中的长.
24.(10分)定义:我们把三角形某边上的中点到这条边上的高的距离称为三角形某边的“中偏度值”.
(1) 如图,在中, ,,,求中边的“中偏度值”;
(2) 在中,,,边上的高,求中边的“中偏度值”.
25.(10分)如图①,在中, ,,,是的中点,点在线段上,连接,作交直线于点,连接.
【初步尝试】
(1) 如图②,当时,线段的长度是____,线段的长度是____;
【结论探究】
(2) 如图①,小宁猜想“”,但她未能想出证明思路,小波介绍了添加辅助线的方法,如表所示,请帮小宁完成证明.
如图,延长至点,使,连接,.
【拓展应用】
如图③,当点在线段的延长线上时,连接,作交直线于点,连接.请补全图形,并求出当时,线段的长.
第十七章质量评估
一、选择题(共10个小题,每题3分,共30分)
1.C 2.D 3.D 4.B 5.A 6.B 7.A 8.D 9.B 10.B
二、填空题(共6个小题,每题3分,共18分)
11.2
12.150
13.
14.5
15.13
16.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(1) 解:,.
(2) ,.
18.(1) 解:.
(2) .
19.解:由题意,得,,.
,即, .
由“远航”号沿东北方向航行可知, ,则 ,
答:“海天”号沿西北方向航行.
20.解:如答图.
第20题答图
由题意,得肘尺,肘尺,肘尺.
设肘尺,则肘尺.
在和中,
,
.
又,,解得.
答:这条鱼出现的地方离较高的棕榈树的树根有20肘尺.
21.(1) 解:,,,,
是直角三角形, ,
,
.
答:修建的公路的长是.
(2) 在中,,
一辆货车从处经过处到处的路程是.
22.(1) 解:学校会受到噪音影响.理由如下:
如答图,过点作于点.
第22题答图
, ,.
,
消防车在公路上沿方向行驶时,学校会受到噪音影响.
(2) 设从点开始学校受到影响,点结束,则,
,.
在中,,
,
消防车的速度为, 学校受影响的时间为.
23.(1) 3
(2) 4
(3) 解:由题意知:,
,,
①,.
,得.
整理得,
.
在中,,,
,
.
24.(1) 解:如答图①,作的中线和高线.
第24题答图①
,,,
.
,
,
,,
为斜边上的中线,,,
,即点到的距离为,
中边的“中偏度值”为.
(2) ①当高在内部时,作的中线,高线,如答图②.
第24题答图②
,,,,
,
,
.
为的中线,,
,即点到的距离为2,
中边的“中偏度值”为2.
②当高在外部时,作的中线,高线,如答图③.
第24题答图③
,,,,
,
,
.
为的中线,,
,
即点到的距离为7,则中边的“中偏度值”为7.
综上所述,中边的“中偏度值”为2或7.
25.(1) 5; 3
(2) 证明:如答图①,延长至点,使,连接,.
第25题答图①
,,,
,
,.
, ,
, ,
.
,,
.
.
(3) 解:如答图②,延长至点,使,连接,.
第25题答图③
设.
同理(2)可证,,
,
,
解得,
.
[时间:120分钟 分值:120分]
一、选择题(共10个小题,每题3分,共30分)
1.在中,斜边,则( )
A.20 B.100 C.200 D.144
2.满足下述条件的三角形中,不是直角三角形的是( )
A.三个内角度数之比为 B.三条边长之比为
C.三条边长分别为41,40,9 D.三条边长分别为,,8
3.若一个三角形三边,,满足,则这个三角形是( )
A.等边三角形 B.钝角三角形
C.等腰直角三角形 D.直角三角形
4.人在平地上以的速度向西走了,接着以的速度向南走了,这时他距离出发点( )
A. B. C. D.
5.如图,所有阴影四边形都是正方形,所有三角形都是直角三角形.已知正方形,,的面积依次为2,4,3,则正方形的面积为( )
第5题图
A.9 B.8 C.27 D.45
6.如图,是等边三角形,边长为2,根据作图的痕迹,则的长为( )
第6题图
A.1.7 B. C. D.
7.如图,在高为,坡面长为的楼梯表面铺地毯,地毯的长度至少需要( )
第7题图
A. B. C. D.
8.图①是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图①中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图②,则图②中大正方形的面积为( )
第8题图
A.24 B.36 C.40 D.44
9.如图,在中, ,为上一点.若,的面积为90,则的长是( )
第9题图
A.6 B.9 C.12 D.
10.《九章算术》是中国古代的数学代表作,书中记载:今有开门去阃(读,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①,②(图②为图①的平面示意图),从点处推开双门,双门间隙的长度为2寸,点和点到门槛的距离都为1尺(1尺寸),则的长是( )
A.104寸 B.101寸 C.52寸 D.50.5寸
二、填空题(共6个小题,每题3分,共18分)
11.如图,一根长为的吸管放在一个圆柱形杯中,测得杯的内部底面直径为,高为,则吸管露出在杯外面的最短长度为____.
第11题图
12.如图,在一根长的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为____.
第12题图
13.将折叠书架画出侧面示意图,为面板架,为支撑架,为锁定杆,可在上移动或固定.已知.如图①,将面板竖直固定时,恰为的中点.如图②,当时,,则支撑架的长度为________.
14.如图,在中, ,,,为上一点.若是的平分线,则____.
第14题图
15.如图是一参赛队员设计的机器人比赛时行走的路径,机器人从处先往东走,又往北走,遇到障碍后又往西走,再转向北走往东拐,仅走就到达了处.,两点之间的距离为__.
第15题图
16.如图,长方体的长、宽、高分别是,,,一只蚂蚁沿着长方体的表面从点爬到点,则蚂蚁爬行的最短路径长为________.
第16题图
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(6分)已知:在中, ,,,.
(1) 若,,求的值;
(2) 若,,求的值.
18.(6分)如图,是平面直角坐标系中的一点.
(1) 用二次根式表示线段的长;
(2) 若,,求的长.
19.(6分)如图,某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行,“海天”号每小时航行.它们离开港口后分别位于点、处,且相距.如果知道“远航”号沿东北方向航行,那么能知道“海天”号沿哪个方向航行吗?
20.(8分)11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题,小溪边长着两棵棕榈树,恰好隔岸相望.一棵树高30肘尺(肘尺是古代的长度单位),另外一棵高20肘尺,两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见棕榈树间的水面上游出一条鱼,它们立刻以同样的速度飞去抓鱼,并且同时到达目标.这条鱼出现的地方离较高的棕榈树的树根有多远?
21.(8分)如图,在笔直的公路旁有一座山,为方便运输货物现要从公路上的处开凿隧道修通一条公路到处,已知处与公路上的停靠站的距离为,与公路上另一停靠站的距离为,停靠站,之间的距离为,且.
(1) 求修建的公路的长;
(2) 若公路修通后,一辆货车从处经过处到处的路程是多少?
22.(9分)如图,公路和公路在点处交汇,且 ,在处有一所中学,,此时有一辆消防车在公路上沿方向以的速度行驶,假设消防车行驶时周围以内有噪音影响.
(1) 学校是否会受到影响?请说明理由.
(2) 如果受到影响,则影响时间是多长?
23.(9分)如图,分别以,,,为边长作正方形.
(1) 若,,则图①中两个正方形的面积之和为____;
(2) 若,,则图②中的长为____;
(3) 已知且满足,,若图①中两个正方形的面积和为2,求图②中的长.
24.(10分)定义:我们把三角形某边上的中点到这条边上的高的距离称为三角形某边的“中偏度值”.
(1) 如图,在中, ,,,求中边的“中偏度值”;
(2) 在中,,,边上的高,求中边的“中偏度值”.
25.(10分)如图①,在中, ,,,是的中点,点在线段上,连接,作交直线于点,连接.
【初步尝试】
(1) 如图②,当时,线段的长度是____,线段的长度是____;
【结论探究】
(2) 如图①,小宁猜想“”,但她未能想出证明思路,小波介绍了添加辅助线的方法,如表所示,请帮小宁完成证明.
如图,延长至点,使,连接,.
【拓展应用】
如图③,当点在线段的延长线上时,连接,作交直线于点,连接.请补全图形,并求出当时,线段的长.
第十七章质量评估
一、选择题(共10个小题,每题3分,共30分)
1.C 2.D 3.D 4.B 5.A 6.B 7.A 8.D 9.B 10.B
二、填空题(共6个小题,每题3分,共18分)
11.2
12.150
13.
14.5
15.13
16.
三、解答题(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题8分,第22、23题每小题9分,第24、25题每小题10分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(1) 解:,.
(2) ,.
18.(1) 解:.
(2) .
19.解:由题意,得,,.
,即, .
由“远航”号沿东北方向航行可知, ,则 ,
答:“海天”号沿西北方向航行.
20.解:如答图.
第20题答图
由题意,得肘尺,肘尺,肘尺.
设肘尺,则肘尺.
在和中,
,
.
又,,解得.
答:这条鱼出现的地方离较高的棕榈树的树根有20肘尺.
21.(1) 解:,,,,
是直角三角形, ,
,
.
答:修建的公路的长是.
(2) 在中,,
一辆货车从处经过处到处的路程是.
22.(1) 解:学校会受到噪音影响.理由如下:
如答图,过点作于点.
第22题答图
, ,.
,
消防车在公路上沿方向行驶时,学校会受到噪音影响.
(2) 设从点开始学校受到影响,点结束,则,
,.
在中,,
,
消防车的速度为, 学校受影响的时间为.
23.(1) 3
(2) 4
(3) 解:由题意知:,
,,
①,.
,得.
整理得,
.
在中,,,
,
.
24.(1) 解:如答图①,作的中线和高线.
第24题答图①
,,,
.
,
,
,,
为斜边上的中线,,,
,即点到的距离为,
中边的“中偏度值”为.
(2) ①当高在内部时,作的中线,高线,如答图②.
第24题答图②
,,,,
,
,
.
为的中线,,
,即点到的距离为2,
中边的“中偏度值”为2.
②当高在外部时,作的中线,高线,如答图③.
第24题答图③
,,,,
,
,
.
为的中线,,
,
即点到的距离为7,则中边的“中偏度值”为7.
综上所述,中边的“中偏度值”为2或7.
25.(1) 5; 3
(2) 证明:如答图①,延长至点,使,连接,.
第25题答图①
,,,
,
,.
, ,
, ,
.
,,
.
.
(3) 解:如答图②,延长至点,使,连接,.
第25题答图③
设.
同理(2)可证,,
,
,
解得,
.
