专题2 勾股定理(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 专题2 勾股定理(含答案)初中数学人教版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 235.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 16:05:21 | ||
图片预览


文档简介
专题2 勾股定理
题型归类 举一反三
题型一 勾股定理的计算
例1 在直角三角形中,如果有一个角是 ,那么这个直角三角形的三边之比是( )
A. B. C. D.
变式跟进
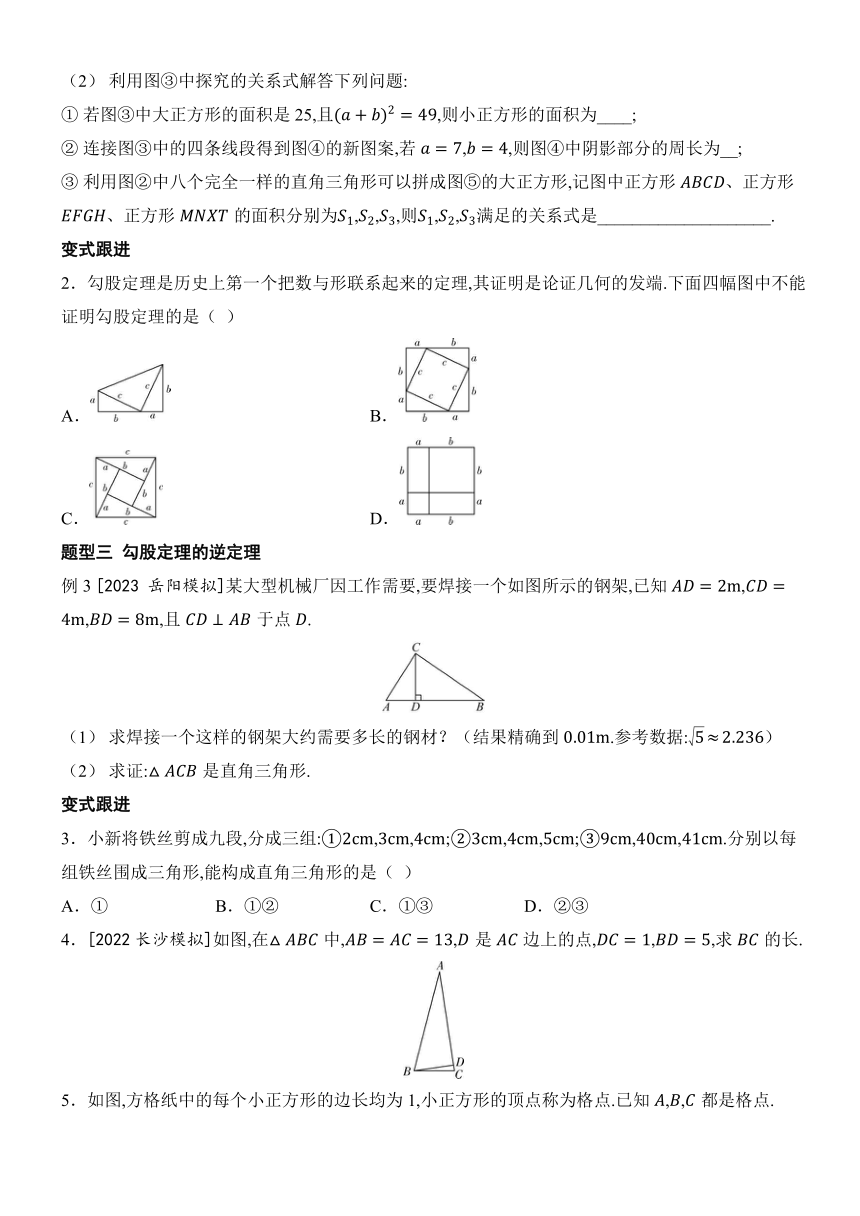
1.如图,在四边形中, , ,,,则的长为( )
A.4 B.5 C. D.
题型二 勾股定理的证明
例2 [2024长沙模拟]【回顾旧知】在学习“乘法公式”时,我们分别从两个不同的角度计算如图①所示的正方形的面积,从而得到公式:.
【类比探究】
(1) 用图②中四个完全一样的直角三角形可以拼成图③的大正方形,请根据图③,利用图形的面积关系,推导,,之间满足的关系式,写出推理过程.
【拓展应用】
(2) 利用图③中探究的关系式解答下列问题:
① 若图③中大正方形的面积是25,且,则小正方形的面积为____;
② 连接图③中的四条线段得到图④的新图案,若,,则图④中阴影部分的周长为__;
③ 利用图②中八个完全一样的直角三角形可以拼成图⑤的大正方形,记图中正方形、正方形、正方形的面积分别为,,,则,,满足的关系式是____________________.
变式跟进
2.勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )
A. B.
C. D.
题型三 勾股定理的逆定理
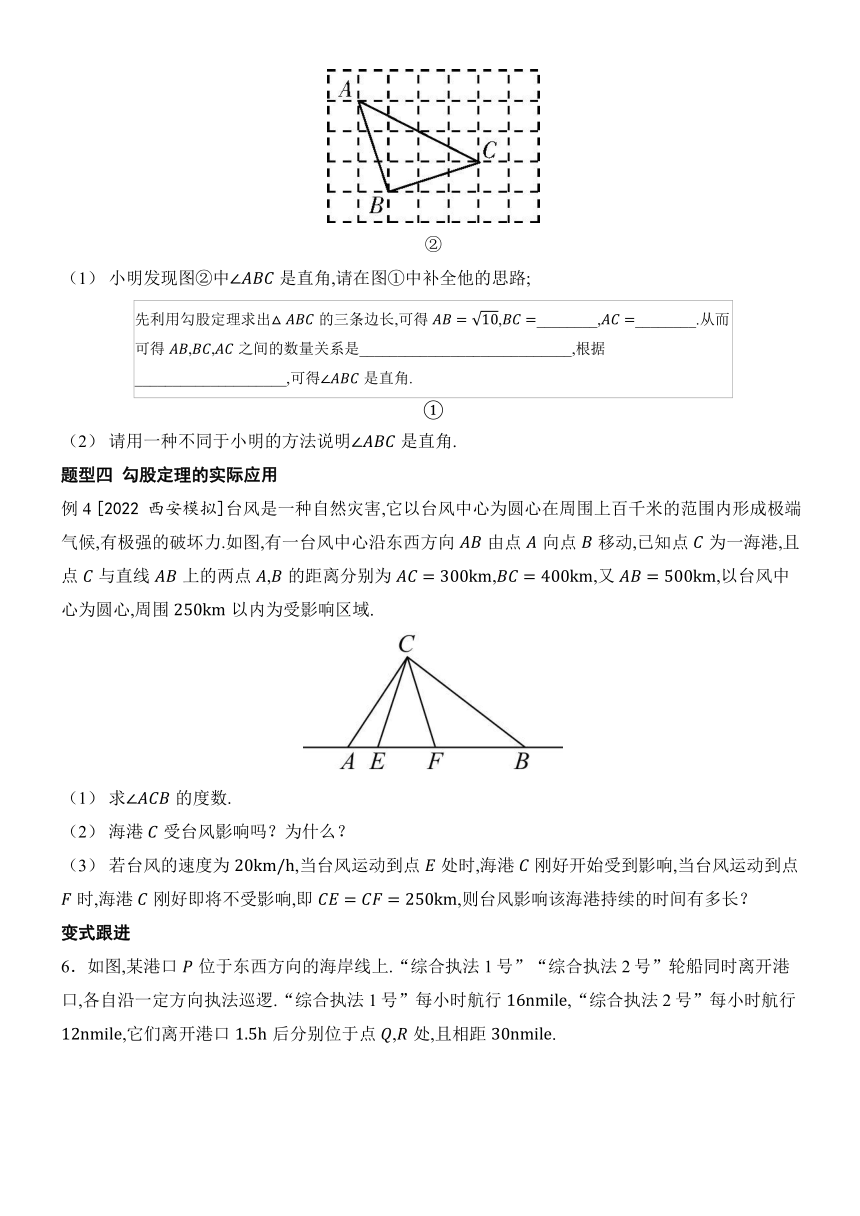
例3 [2023 岳阳模拟]某大型机械厂因工作需要,要焊接一个如图所示的钢架,已知,,,且于点.
(1) 求焊接一个这样的钢架大约需要多长的钢材?(结果精确到.参考数据:)
(2) 求证:是直角三角形.
变式跟进
3.小新将铁丝剪成九段,分成三组:,,;,,;,,.分别以每组铁丝围成三角形,能构成直角三角形的是( )
A.① B.①② C.①③ D.②③
4.[2022长沙模拟]如图,在中,,是边上的点,,,求的长.
5.如图,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点.已知,,都是格点.
②
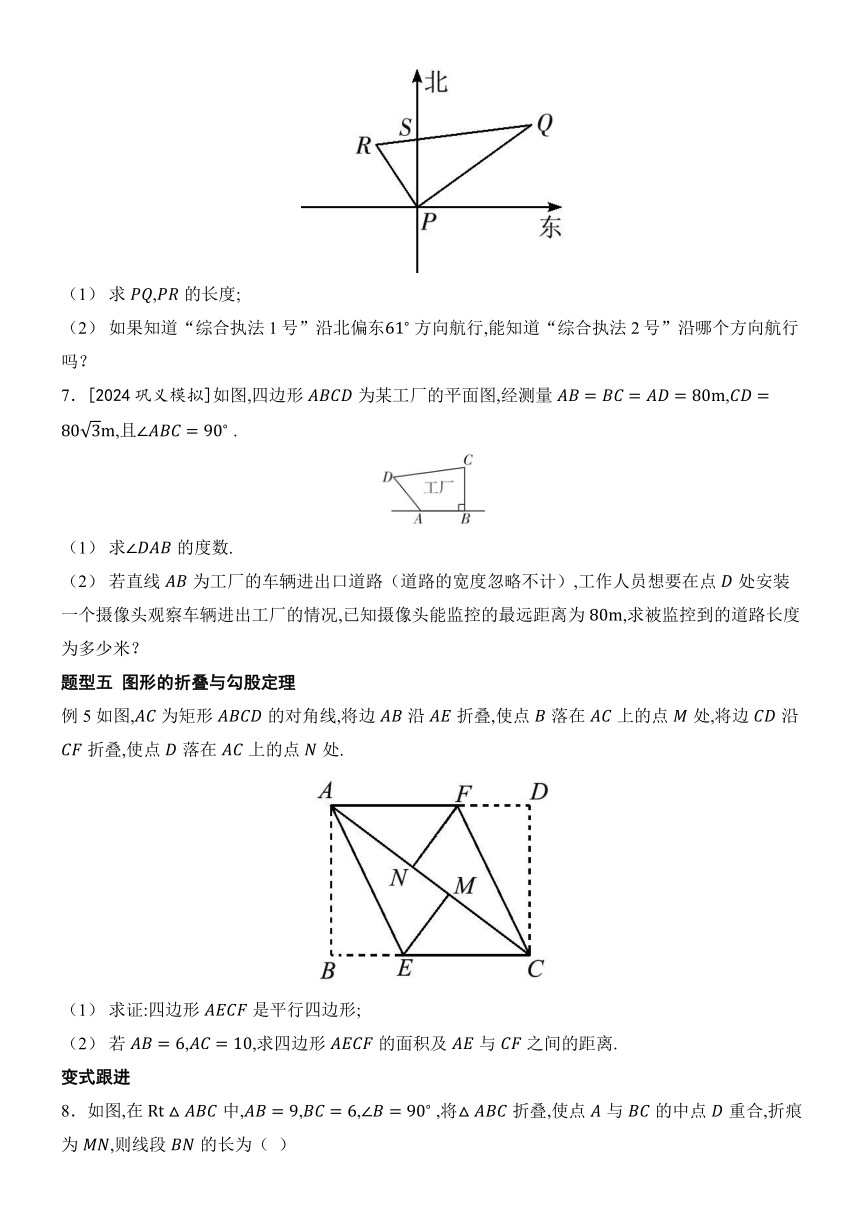
(1) 小明发现图②中是直角,请在图①中补全他的思路;
先利用勾股定理求出的三条边长,可得,________,________.从而可得,,之间的数量关系是____________________________,根据____________________,可得是直角.
(2) 请用一种不同于小明的方法说明是直角.
题型四 勾股定理的实际应用
例4 [2022 西安模拟]台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向由点向点移动,已知点为一海港,且点与直线上的两点,的距离分别为,,又,以台风中心为圆心,周围以内为受影响区域.
(1) 求的度数.
(2) 海港受台风影响吗?为什么?
(3) 若台风的速度为,当台风运动到点处时,海港刚好开始受到影响,当台风运动到点时,海港刚好即将不受影响,即,则台风影响该海港持续的时间有多长?
变式跟进
6.如图,某港口位于东西方向的海岸线上.“综合执法1号”“综合执法2号”轮船同时离开港口,各自沿一定方向执法巡逻.“综合执法1号”每小时航行,“综合执法2号”每小时航行,它们离开港口后分别位于点,处,且相距.
(1) 求,的长度;
(2) 如果知道“综合执法1号”沿北偏东 方向航行,能知道“综合执法2号”沿哪个方向航行吗?
7.[2024巩义模拟]如图,四边形为某工厂的平面图,经测量,,且 .
(1) 求的度数.
(2) 若直线为工厂的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点处安装一个摄像头观察车辆进出工厂的情况,已知摄像头能监控的最远距离为,求被监控到的道路长度为多少米?
题型五 图形的折叠与勾股定理
例5 如图,为矩形的对角线,将边沿折叠,使点落在上的点处,将边沿折叠,使点落在上的点处.
(1) 求证:四边形是平行四边形;
(2) 若,,求四边形的面积及与之间的距离.
变式跟进
8.如图,在中,,, ,将折叠,使点与的中点重合,折痕为,则线段的长为( )
A. B. C.4 D.5
9.如图,将矩形纸片折叠,使点与点重合,折痕分别与,交于点,.
(1) 求证:;
(2) 若,,求的面积.
题型六 空间线路中两点间的最短距离
例6 如图,一个圆柱高,底面周长为,一只蚂蚁从点沿侧面爬到正对面的点处吃食,要爬行的最短路程是________.
变式跟进
10.如图为一个长方体盒子,,,则沿盒子表面从点到点的最短路程是________.
过关训练 现复活用
A组·基础达标 逐点击破
1.在中,已知两直角边长分别为,,则斜边的长为( )
A.2 B.4 C. D.
2.如图,公路,互相垂直,公路的中点与点被湖隔开.若测得,,则,两点间的距离为( )
第2题图
A. B. C. D.
3.如图,一艘巡逻船由港沿北偏西 方向航行至岛,然后再沿北偏东 方向航行至港,则,两港相距( )
第3题图
A. B. C. D.
4.已知,是线段上的两点,,,以点为圆心,的长为半径画弧,再以点为圆心,的长为半径画弧,两弧交于点,连接,,则一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B组·能力提升 强化突破
5.[2024百色模拟]学习了“勾股定理”后,某校数学兴趣小组的同学把“测量风筝的垂直高度”作为一项课题活动,利用课余时间完成了实践调查,并形成了如下的活动报告,请根据活动报告解答下列问题.
报告 测量风筝的垂直高度
成员 组长:;组员:,,
工具 皮尺等
示意图
方案 先测量水平距离,然后根据手中剩余线的长度得出风筝线长,最后测量放风筝的同学的身高
数据 ,,
评价 ……
(1) 求此时风筝的垂直高度;
(2) 若站在点不动,想把风筝沿方向从点的位置上升至点的位置,则还需放出风筝线多少米?
专题2 勾股定理
题型归类 举一反三
题型一 勾股定理的计算
【点悟】 勾股定理的作用是已知直角三角形的任意两边,求第三边的长,我们要会灵活运用勾股定理的不同形式求解.在 中, ,,,所对的边分别为,,,则勾股定理有如下不同的形式:
(1),,;
(2),,.
例1 D
变式跟进
1.D
题型二 勾股定理的证明
例2 (1) 解: 大正方形的边长为,
大正方形的面积为.
大正方形由四个直角边长为,的直角三角形和一个边长为的小正方形组成, 大正方形的面积为.
.
.
(2) ① 1
② 36
③
变式跟进
2.D
题型三 勾股定理的逆定理
例3 (1) 解:,
.
,,,
,
,
.
答:焊接一个这样的钢架大约需要长的钢材.
(2) 证明:,,
.
,
,
,
是直角三角形.
变式跟进
3.D
4.解:,,
.
在中,,,,
,
,
,
是直角三角形,且 .
在中,,,
.
5.(1) ; ; ; 勾股定理的逆定理
(2) 解:如答图,过点作于点,过点作于点.
由图可知,,,.
在和中,
,
.
在中, ,
.
,,三点共线,
,
,
是直角.
变式跟进5答图
题型四 勾股定理的实际应用
例4 (1) 解:,,,
,
是直角三角形, .
(2) 海港受台风影响.理由如下:
如答图,过点作于点.
例4答图
是直角三角形,
,
.
以台风中心为圆心,周围以内为受影响区域, 海港受台风影响.
(3) 当,时,正好影响港口,
,
.
台风的速度为,
.
台风影响该海港持续的时间为.
变式跟进
6.(1) 解:,
.
(2) ,,
,且,
是直角三角形,且 .
“综合执法1号”沿北偏东 方向航行, ,
,
“综合执法2号”沿北偏西 方向航行.
7.(1) 解:如答图,连接.
变式跟进7答图
, ,
是等腰直角三角形,
, .
在中,,
是直角三角形,且 ,
.
(2) 如答图,过点作于点,作点关于的对称点,连接.
由轴对称的性质,得,.
由(1)知, ,
,
是等腰直角三角形,
,
,
被监控到的道路长度为.
题型五 图形的折叠与勾股定理
【点悟】 解决有关折叠的问题时,通常利用勾股定理这个等量关系建立方程.折叠前后两图形全等,即对应线段相等,对应角相等,对应点的连线段被折痕垂直平分.
例5 (1) 证明: 四边形是矩形,
,,
,.
由折叠的性质,得
,,
又,
,,
四边形是平行四边形.
(2) 解:在中,,,
根据勾股定理,得.
,
.
设,则.
在中,由勾股定理,得
,
即,解得.
故.
在中,由勾股定理,得
.
设与之间的距离为,
则,即,
解得.
与之间的距离为.
变式跟进
8.C
9.(1) 证明: 四边形是矩形,
,.
,
,
.
在和中,
.
(2) 解:由折叠的性质,得.
设,
则.
在中,,
,解得.
,
,
.
题型六 空间线路中两点间的最短距离
【点悟】 几何体的表面上两点间的最短路线问题的解决方法是将几何体表面展开,即将立体问题转化为平面问题,然后利用“两点之间,线段最短”确定最短路线,最后利用勾股定理计算.
例6
变式跟进
10.
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.C 3.B 4.B
B组·能力提升 强化突破
5.(1) 解:由题意,得,
在中,,
.
答:此时风筝的垂直高度为.
(2) 由题意,得,
,
,
在中,,
.
答:还需放出风筝线.
题型归类 举一反三
题型一 勾股定理的计算
例1 在直角三角形中,如果有一个角是 ,那么这个直角三角形的三边之比是( )
A. B. C. D.
变式跟进
1.如图,在四边形中, , ,,,则的长为( )
A.4 B.5 C. D.
题型二 勾股定理的证明
例2 [2024长沙模拟]【回顾旧知】在学习“乘法公式”时,我们分别从两个不同的角度计算如图①所示的正方形的面积,从而得到公式:.
【类比探究】
(1) 用图②中四个完全一样的直角三角形可以拼成图③的大正方形,请根据图③,利用图形的面积关系,推导,,之间满足的关系式,写出推理过程.
【拓展应用】
(2) 利用图③中探究的关系式解答下列问题:
① 若图③中大正方形的面积是25,且,则小正方形的面积为____;
② 连接图③中的四条线段得到图④的新图案,若,,则图④中阴影部分的周长为__;
③ 利用图②中八个完全一样的直角三角形可以拼成图⑤的大正方形,记图中正方形、正方形、正方形的面积分别为,,,则,,满足的关系式是____________________.
变式跟进
2.勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )
A. B.
C. D.
题型三 勾股定理的逆定理
例3 [2023 岳阳模拟]某大型机械厂因工作需要,要焊接一个如图所示的钢架,已知,,,且于点.
(1) 求焊接一个这样的钢架大约需要多长的钢材?(结果精确到.参考数据:)
(2) 求证:是直角三角形.
变式跟进
3.小新将铁丝剪成九段,分成三组:,,;,,;,,.分别以每组铁丝围成三角形,能构成直角三角形的是( )
A.① B.①② C.①③ D.②③
4.[2022长沙模拟]如图,在中,,是边上的点,,,求的长.
5.如图,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点.已知,,都是格点.
②
(1) 小明发现图②中是直角,请在图①中补全他的思路;
先利用勾股定理求出的三条边长,可得,________,________.从而可得,,之间的数量关系是____________________________,根据____________________,可得是直角.
(2) 请用一种不同于小明的方法说明是直角.
题型四 勾股定理的实际应用
例4 [2022 西安模拟]台风是一种自然灾害,它以台风中心为圆心在周围上百千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向由点向点移动,已知点为一海港,且点与直线上的两点,的距离分别为,,又,以台风中心为圆心,周围以内为受影响区域.
(1) 求的度数.
(2) 海港受台风影响吗?为什么?
(3) 若台风的速度为,当台风运动到点处时,海港刚好开始受到影响,当台风运动到点时,海港刚好即将不受影响,即,则台风影响该海港持续的时间有多长?
变式跟进
6.如图,某港口位于东西方向的海岸线上.“综合执法1号”“综合执法2号”轮船同时离开港口,各自沿一定方向执法巡逻.“综合执法1号”每小时航行,“综合执法2号”每小时航行,它们离开港口后分别位于点,处,且相距.
(1) 求,的长度;
(2) 如果知道“综合执法1号”沿北偏东 方向航行,能知道“综合执法2号”沿哪个方向航行吗?
7.[2024巩义模拟]如图,四边形为某工厂的平面图,经测量,,且 .
(1) 求的度数.
(2) 若直线为工厂的车辆进出口道路(道路的宽度忽略不计),工作人员想要在点处安装一个摄像头观察车辆进出工厂的情况,已知摄像头能监控的最远距离为,求被监控到的道路长度为多少米?
题型五 图形的折叠与勾股定理
例5 如图,为矩形的对角线,将边沿折叠,使点落在上的点处,将边沿折叠,使点落在上的点处.
(1) 求证:四边形是平行四边形;
(2) 若,,求四边形的面积及与之间的距离.
变式跟进
8.如图,在中,,, ,将折叠,使点与的中点重合,折痕为,则线段的长为( )
A. B. C.4 D.5
9.如图,将矩形纸片折叠,使点与点重合,折痕分别与,交于点,.
(1) 求证:;
(2) 若,,求的面积.
题型六 空间线路中两点间的最短距离
例6 如图,一个圆柱高,底面周长为,一只蚂蚁从点沿侧面爬到正对面的点处吃食,要爬行的最短路程是________.
变式跟进
10.如图为一个长方体盒子,,,则沿盒子表面从点到点的最短路程是________.
过关训练 现复活用
A组·基础达标 逐点击破
1.在中,已知两直角边长分别为,,则斜边的长为( )
A.2 B.4 C. D.
2.如图,公路,互相垂直,公路的中点与点被湖隔开.若测得,,则,两点间的距离为( )
第2题图
A. B. C. D.
3.如图,一艘巡逻船由港沿北偏西 方向航行至岛,然后再沿北偏东 方向航行至港,则,两港相距( )
第3题图
A. B. C. D.
4.已知,是线段上的两点,,,以点为圆心,的长为半径画弧,再以点为圆心,的长为半径画弧,两弧交于点,连接,,则一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B组·能力提升 强化突破
5.[2024百色模拟]学习了“勾股定理”后,某校数学兴趣小组的同学把“测量风筝的垂直高度”作为一项课题活动,利用课余时间完成了实践调查,并形成了如下的活动报告,请根据活动报告解答下列问题.
报告 测量风筝的垂直高度
成员 组长:;组员:,,
工具 皮尺等
示意图
方案 先测量水平距离,然后根据手中剩余线的长度得出风筝线长,最后测量放风筝的同学的身高
数据 ,,
评价 ……
(1) 求此时风筝的垂直高度;
(2) 若站在点不动,想把风筝沿方向从点的位置上升至点的位置,则还需放出风筝线多少米?
专题2 勾股定理
题型归类 举一反三
题型一 勾股定理的计算
【点悟】 勾股定理的作用是已知直角三角形的任意两边,求第三边的长,我们要会灵活运用勾股定理的不同形式求解.在 中, ,,,所对的边分别为,,,则勾股定理有如下不同的形式:
(1),,;
(2),,.
例1 D
变式跟进
1.D
题型二 勾股定理的证明
例2 (1) 解: 大正方形的边长为,
大正方形的面积为.
大正方形由四个直角边长为,的直角三角形和一个边长为的小正方形组成, 大正方形的面积为.
.
.
(2) ① 1
② 36
③
变式跟进
2.D
题型三 勾股定理的逆定理
例3 (1) 解:,
.
,,,
,
,
.
答:焊接一个这样的钢架大约需要长的钢材.
(2) 证明:,,
.
,
,
,
是直角三角形.
变式跟进
3.D
4.解:,,
.
在中,,,,
,
,
,
是直角三角形,且 .
在中,,,
.
5.(1) ; ; ; 勾股定理的逆定理
(2) 解:如答图,过点作于点,过点作于点.
由图可知,,,.
在和中,
,
.
在中, ,
.
,,三点共线,
,
,
是直角.
变式跟进5答图
题型四 勾股定理的实际应用
例4 (1) 解:,,,
,
是直角三角形, .
(2) 海港受台风影响.理由如下:
如答图,过点作于点.
例4答图
是直角三角形,
,
.
以台风中心为圆心,周围以内为受影响区域, 海港受台风影响.
(3) 当,时,正好影响港口,
,
.
台风的速度为,
.
台风影响该海港持续的时间为.
变式跟进
6.(1) 解:,
.
(2) ,,
,且,
是直角三角形,且 .
“综合执法1号”沿北偏东 方向航行, ,
,
“综合执法2号”沿北偏西 方向航行.
7.(1) 解:如答图,连接.
变式跟进7答图
, ,
是等腰直角三角形,
, .
在中,,
是直角三角形,且 ,
.
(2) 如答图,过点作于点,作点关于的对称点,连接.
由轴对称的性质,得,.
由(1)知, ,
,
是等腰直角三角形,
,
,
被监控到的道路长度为.
题型五 图形的折叠与勾股定理
【点悟】 解决有关折叠的问题时,通常利用勾股定理这个等量关系建立方程.折叠前后两图形全等,即对应线段相等,对应角相等,对应点的连线段被折痕垂直平分.
例5 (1) 证明: 四边形是矩形,
,,
,.
由折叠的性质,得
,,
又,
,,
四边形是平行四边形.
(2) 解:在中,,,
根据勾股定理,得.
,
.
设,则.
在中,由勾股定理,得
,
即,解得.
故.
在中,由勾股定理,得
.
设与之间的距离为,
则,即,
解得.
与之间的距离为.
变式跟进
8.C
9.(1) 证明: 四边形是矩形,
,.
,
,
.
在和中,
.
(2) 解:由折叠的性质,得.
设,
则.
在中,,
,解得.
,
,
.
题型六 空间线路中两点间的最短距离
【点悟】 几何体的表面上两点间的最短路线问题的解决方法是将几何体表面展开,即将立体问题转化为平面问题,然后利用“两点之间,线段最短”确定最短路线,最后利用勾股定理计算.
例6
变式跟进
10.
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.C 3.B 4.B
B组·能力提升 强化突破
5.(1) 解:由题意,得,
在中,,
.
答:此时风筝的垂直高度为.
(2) 由题意,得,
,
,
在中,,
.
答:还需放出风筝线.
