专题4 一次函数(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 专题4 一次函数(含答案)初中数学人教版八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 301.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 16:05:59 | ||
图片预览




文档简介
专题4 一次函数
题型归类 举一反三
题型一 函数的概念及图象
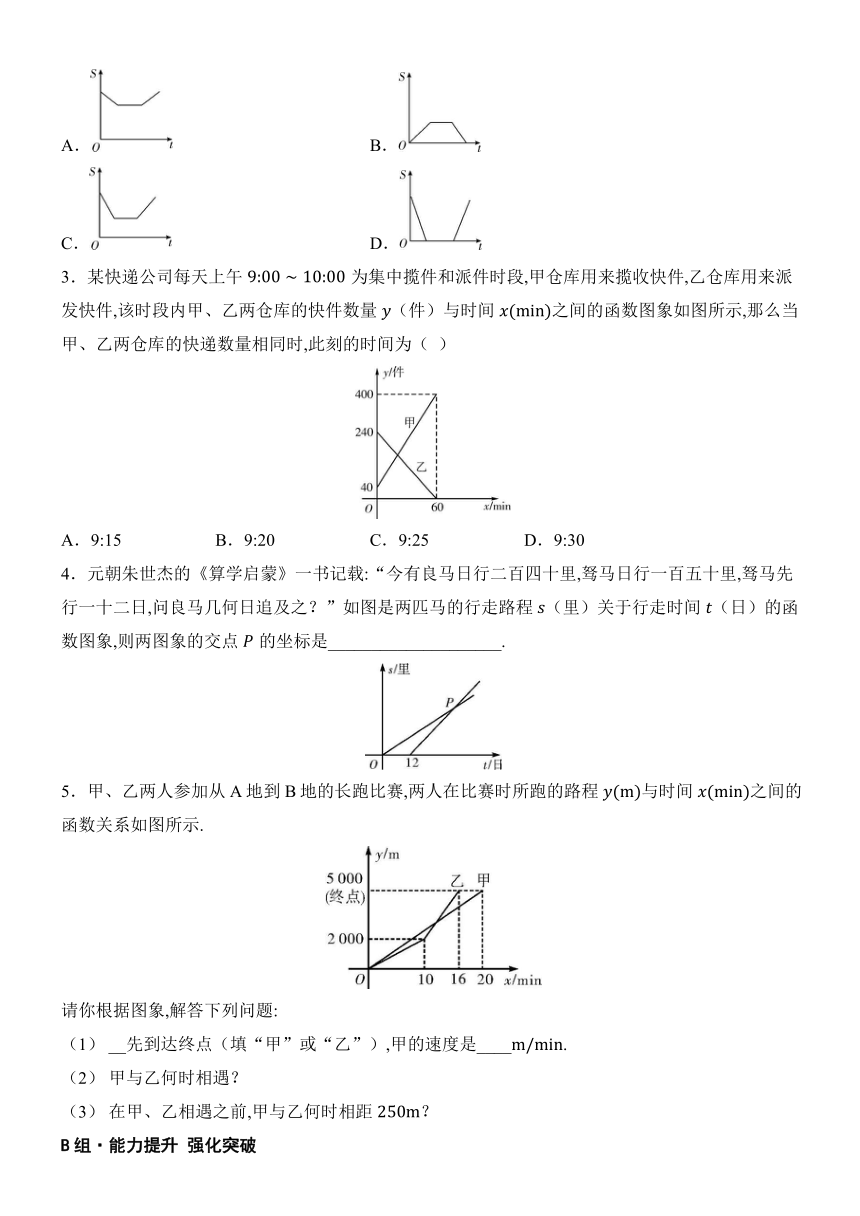
例1 一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,则下列说法正确的有( )
①快车追上慢车需;
②慢车比快车早出发;
③快车的速度为;
④慢车的速度为;
,B两地相距.
A.2个 B.3个 C.4个 D.5个
变式跟进
1.已知林茂的家、体育场、文具店在同一直线上,图中信息反映的是林茂从家跑步去体育场,在体育场锻炼了一段时间后又走到文具店买笔,然后再走回家的过程.图中表示时间,表示林茂离家的距离.根据图中的信息,下列说法错误的是( )
A.体育场离林茂家
B.体育场离文具店
C.林茂从体育场出发到文具店的平均速度是
D.林茂从文具店回家的平均速度是
题型二 一次函数的图象与性质
例2 当时,一次函数的图象大致是( )
A. B.
C. D.
变式跟进
2.已知一次函数和,则函数和的图象可能是( )
A. B.
C. D.
题型三 求一次函数的解析式
例3 已知一次函数的图象经过,两点.
(1) 求一次函数的解析式;
(2) 若一次函数的图象与轴的交点为,求的值.
变式跟进
3.已知一次函数的图象经过,两点.
(1) 求这个一次函数的解析式;
(2) 将该函数的图象向上平移3个单位长度,求平移后的图象与轴的交点的坐标.
题型四 一次函数与一元一次不等式(组)、方程(组)
例4 如图,一次函数的图象经过点,当时,的取值范围为________.
变式跟进
4.如图,一次函数与的图象交于点,则关于的不等式组的解集为____________.
题型五 一次函数的实际应用
例5 [2023遂宁]端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售.经了解,每个乙种粽子的进价比每个甲种粽子的进价多2元,用1 000元购进甲种粽子的数量与用1 200元购进乙种粽子的数量相同.
(1) 甲、乙两种粽子每个的进价分别是多少元?
(2) 该超市计划购进这两种粽子共200个(两种都有),其中甲种粽子的数量不低于乙种粽子数量的2倍,若甲、乙两种粽子的售价分别为12元/个、15元/个,设购进甲种粽子个,两种粽子全部售完时获得的利润为元.
① 求关于的函数解析式,并求出的取值范围.
② 超市应如何进货才能获得最大利润,最大利润是多少元?
变式跟进
5.[2024常德模拟]甲、乙两车分别从地将一批物品运往地,再返回地,如图表示两车离地的距离随时间变化的图象,已知乙车到达地后以的速度返回.请根据图象所给的信息,解答下列问题:
(1) 甲车从地到地的速度是________________,甲车出发____后被乙车追上.
(2) 甲车与乙车在距离地多远处迎面相遇?
(3) 当甲车从地返回的速度满足什么条件时,才能比乙车先回到地?
题型六 一次函数的综合
例6 [2024长沙模拟]如图①,在平面直角坐标系中,正方形的边在轴上,是的中点,直线过定点,交轴于点.
(1) 求点的坐标.
(2) 如图②,当时,过点作,交于点,在直线上是否存在点,使得是等腰直角三角形?若存在,请求出所有满足条件的点;若不存在,请说明理由.
(3) 点在直线上,且,连接,为的中点,连接.求线段的长度的最大值,并直接写出此时点的坐标.
变式跟进
6.[2024娄底模拟]如图①,在平面直角坐标系中,一次函数的图象分别交轴、轴于点,,一次函数的图象经过点,并与轴交于点,是直线上的一个动点.
(1) 直线的解析式为____________,点的坐标为____________.
(2) 若的面积为18,求点的坐标.
(3) 如图②,在(2)的条件下,当点在轴上方时,过点作轴的垂线,交直线于点是轴上一点,在直线上找一点,使以,,,为顶点的四边形是以为边的平行四边形,请直接写出点的坐标.
过关训练 现复活用
A组·基础达标 逐点击破
1.如果一次函数,是常数的图象不经过第二象限,那么,应满足的条件是( )
A.且 B.且
C.且 D.且
2.[2022仙桃、潜江、天门]如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形.设穿过的时间为,大正方形的面积为,小正方形与大正方形重叠部分的面积为.若,则随变化的函数图象大致为( )
A. B.
C. D.
3.某快递公司每天上午为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量(件)与时间之间的函数图象如图所示,那么当甲、乙两仓库的快递数量相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
4.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”如图是两匹马的行走路程(里)关于行走时间(日)的函数图象,则两图象的交点的坐标是____________________.
5.甲、乙两人参加从A地到B地的长跑比赛,两人在比赛时所跑的路程与时间之间的函数关系如图所示.
请你根据图象,解答下列问题:
(1) __先到达终点(填“甲”或“乙”),甲的速度是____.
(2) 甲与乙何时相遇?
(3) 在甲、乙相遇之前,甲与乙何时相距?
B组·能力提升 强化突破
6.[2024汨罗模拟]如图,在平面直角坐标系中,矩形的边,边,直线与矩形的边和都有交点,交点分别是点,.
(1) 请用含的代数式分别表示点和点的坐标:________________,________________;
(2) 当四边形为平行四边形时,求的值.
7.[2024宁乡模拟]如图,在平面直角坐标系中,直线与直线相交于点,分别交坐标轴于点,,,.
(1) 求和的值;
(2) 如图,是直线上的一个动点,设点的横坐标为,当时,求点的坐标;
(3) 直线上有一点,在平面内找一点,使得以为一边,以,,,为顶点的四边形是菱形,请写出符合条件的点的坐标.
8.[2024湘西州模拟改编]我们不妨约定:在平面直角坐标系中,将点称为“芙蓉点”,经过点的函数,称为“芙蓉函数”.
(1) 有函数:;;.其中函数____(填序号)是“芙蓉函数”.
(2) 已知“芙蓉函数”的图象经过点,求该“芙蓉函数”的解析式.
(3) 若直线与轴、轴分别交于点,,是轴上一点,若将沿直线折叠,点恰好落在轴上的点处.试问经过,两点的一次函数是否可以为“芙蓉函数”?若可以,请直接写出所有函数解析式;若不可以,请说明理由.
9.[2024衡阳模拟]如图,已知矩形的顶点在坐标原点,点,分别在轴、轴的正半轴上,顶点,直线经过点交于点、交轴于点,是的中点,直线交于点.
(1) 求点的坐标及直线的函数解析式.
(2) 求的面积,并在直线上找一点,使,并求出点的坐标.
(3) 在轴上有一点,过点作轴的垂线,分别交直线,于点,,在线段上是否存在一点,使得为等腰直角三角形 若存在,请求出点的坐标;若不存在,请说明理由.
专题4 一次函数
题型归类 举一反三
题型一 函数的概念及图象
【点悟】 解决这类函数图象描述事物变化规律的问题,关键是正确分析事物的变化过程,理解函数图象的横、纵坐标的含义,同时要注意函数自变量的取值范围.
例1 B
变式跟进
1.C
题型二 一次函数的图象与性质
【点悟】 一次函数 的图象和性质与解析式中的系数,有关,如下表:
, , , ,
图象
经过象限 一、二、三 一、三、四 一、二、四 二、三、四
增减性 随 的增大而增大 随 的增大而增大 随 的增大而减小 随 的增大而减小
例2 B
变式跟进
2.A
题型三 求一次函数的解析式
【点悟】 求一次函数 的解析式时,把已知点的坐标代入解析式,运用待定系数法求出,;求一次函数与坐标轴的交点坐标时,是根据坐标轴的坐标特征代入解析式求出符合题意的解.
例3 (1) 解:由题意,得解得
一次函数的解析式为.
(2) ,
当时,,即.
变式跟进
3.(1) 解:设一次函数的解析式为.
将点,代入,
得解得
一次函数的解析式为.
(2) 将的图象向上平移3个单位长度,
平移后的直线的解析式为.
在中,令,得,
平移后的图象与轴的交点的坐标为.
题型四 一次函数与一元一次不等式(组)、方程(组)
例4
变式跟进
4.
题型五 一次函数的实际应用
例5 (1) 解:设每个甲种粽子的进价为元,则每个乙种粽子的进价为元,
由题意,得,解得.
经检验,是原方程的根,且符合题意,
此时.
答:每个甲种粽子的进价为10元,每个乙种粽子的进价为12元.
(2) ① 设购进甲种粽子个,则购进乙种粽子个,
由题意,得,
关于的函数解析式为.
甲种粽子的数量不低于乙种粽子数量的2倍,
,解得.
的取值范围为,为正整数.
② 由①知,,,为正整数,
随的增大而减小,
当时,有最大值,最大值为,此时(个).
答:当购进甲种粽子134个,乙种粽子66个时,获得利润最大,最大利润为466元.
变式跟进
5.(1) ; 1.5
(2) 解:设乙车从地到地的解析式为,将点,代入,得解得
,
当时,,
设乙车从地到地的解析式为,
将点代入,得
,
解得,
.
当两车迎面相遇时,,
解得,
将代入,得.
答:甲车与乙车在距离地处迎面相遇.
(3) 当乙车返回地时,有,
解得,
甲车要比乙车先回到地,速度要大于.
答:当甲车从地返回的速度大于时,才能比乙车先回到地.
题型六 一次函数的综合
例6 (1) 解:,
,
当时,,
直线过定点,
.
(2) 存在.
当时,直线的函数解析式为.
当时,,
.
正方形的边在轴上,是的中点,,
,,, ,
.
如答图①,过点作交的延长线于点,
例6答图①
则,.
,
,
,
,
,
为等腰直角三角形.
点在直线上,且是等腰直角三角形,
当点与点重合时,满足题意,此时.
当点在点上方,且时,满足题意,即为的中点,
.
综上所述,或.
(3) 如答图②,取点,连接,,则,
例6答图②
为的中点,.
为的中点,
.
,
当,,三点共线,即点在的延长线上时,有最大值为的长,此时的值最大,如答图②.
,
的最大值为,
的最大值为,
此时.
变式跟进
6.(1) ;
(2) 解:设点,
点的坐标为,点的坐标为,
.
,
,
.
当时,;
当时,.
点的坐标为或.
(3) 点在轴上方,
.
当时,,
,
.
设点,则,
,
当时,以,,,为顶点的四边形是以为边的平行四边形,
,
解得或,
当时,,;
当时,,,
点的坐标为或.
过关训练 现复活用
A组·基础达标 逐点击破
1.B 2.A 3.B
4.
5.(1) 乙; 250
(2) 解:设甲跑的路程与时间之间的函数解析式为.
由图象,可得.
设当时,乙跑的路程与时间之间的函数解析式为.
由图象,可得
解得
当时,乙跑的路程与时间之间的函数解析式为.
联立解得
甲与乙在时相遇.
(3) 设甲、乙相遇之前,经过的时间为时,甲与乙相距.
由题意,得或,
解得或.
在甲、乙相遇之前,经过或时甲与乙相距.
B组·能力提升 强化突破
6.(1) ;
(2) 解: 四边形是矩形,,,
,,,
由(1)知,点,的坐标分别为,,
则,.
当四边形为平行四边形时,则,即,
解得.
7.(1) 解:将点代入,得,解得,
点.
将点代入,得,
解得,
,.
(2) 由(1)得直线的解析式为,
点,
,
解得或,
点的坐标是或.
(3) 设点,点.
由(1)知,点,的坐标分别为,,
则.
当是边时,
当点在点的上方时,则,即,
解得,
点或,
此时点在点的正下方5个单位长度,
则点或;
当点在点的下方时,则,不符合题意;
当是对角线时,点,的纵坐标为,则,
解得,则点的横坐标为5,
点的坐标为.
综上所述,点的坐标为或或.
8.(1) ②
(2) 解: “芙蓉函数”的图象经过点,
的图象也经过点,
解得
该“芙蓉函数”的解析式为.
(3) 存在“芙蓉函数”.
9.(1) 解: 四边形为矩形,点的坐标为,
点的坐标为,轴.
直线经过点,
,
,
直线的函数解析式为.
当时,有,
解得,
点的坐标为.
是的中点,
点的坐标为,即,
直线的函数解析式为.
(2)
.
当时,,
点的坐标为.
设点的坐标为.
,
,
解得或,
点的坐标为或.
(3) 点的坐标为,
点的坐标为,点的坐标为.
分三种情况:
①当 时,如答图①所示,
第9题答图①
为等腰直角三角形,
,即,
解得,
,
此时点的坐标为;
②当 时,如答图②所示,
第9题答图②
为等腰直角三角形,
,即,
解得,
,
此时点的坐标为;
③当 时,过点作于点,如答图③所示.
第9题答图③
为等腰直角三角形,
,即或,
解得或,
当时,点的坐标为,点的坐标为,
此时点的坐标为;
当时,点的坐标为,点的坐标为,
此时点的坐标为.
综上所述,在线段上存在一点,使得为等腰直角三角形;点的坐标为或或或.
题型归类 举一反三
题型一 函数的概念及图象
例1 一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,则下列说法正确的有( )
①快车追上慢车需;
②慢车比快车早出发;
③快车的速度为;
④慢车的速度为;
,B两地相距.
A.2个 B.3个 C.4个 D.5个
变式跟进
1.已知林茂的家、体育场、文具店在同一直线上,图中信息反映的是林茂从家跑步去体育场,在体育场锻炼了一段时间后又走到文具店买笔,然后再走回家的过程.图中表示时间,表示林茂离家的距离.根据图中的信息,下列说法错误的是( )
A.体育场离林茂家
B.体育场离文具店
C.林茂从体育场出发到文具店的平均速度是
D.林茂从文具店回家的平均速度是
题型二 一次函数的图象与性质
例2 当时,一次函数的图象大致是( )
A. B.
C. D.
变式跟进
2.已知一次函数和,则函数和的图象可能是( )
A. B.
C. D.
题型三 求一次函数的解析式
例3 已知一次函数的图象经过,两点.
(1) 求一次函数的解析式;
(2) 若一次函数的图象与轴的交点为,求的值.
变式跟进
3.已知一次函数的图象经过,两点.
(1) 求这个一次函数的解析式;
(2) 将该函数的图象向上平移3个单位长度,求平移后的图象与轴的交点的坐标.
题型四 一次函数与一元一次不等式(组)、方程(组)
例4 如图,一次函数的图象经过点,当时,的取值范围为________.
变式跟进
4.如图,一次函数与的图象交于点,则关于的不等式组的解集为____________.
题型五 一次函数的实际应用
例5 [2023遂宁]端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.某超市为了满足人们的需求,计划在端午节前购进甲、乙两种粽子进行销售.经了解,每个乙种粽子的进价比每个甲种粽子的进价多2元,用1 000元购进甲种粽子的数量与用1 200元购进乙种粽子的数量相同.
(1) 甲、乙两种粽子每个的进价分别是多少元?
(2) 该超市计划购进这两种粽子共200个(两种都有),其中甲种粽子的数量不低于乙种粽子数量的2倍,若甲、乙两种粽子的售价分别为12元/个、15元/个,设购进甲种粽子个,两种粽子全部售完时获得的利润为元.
① 求关于的函数解析式,并求出的取值范围.
② 超市应如何进货才能获得最大利润,最大利润是多少元?
变式跟进
5.[2024常德模拟]甲、乙两车分别从地将一批物品运往地,再返回地,如图表示两车离地的距离随时间变化的图象,已知乙车到达地后以的速度返回.请根据图象所给的信息,解答下列问题:
(1) 甲车从地到地的速度是________________,甲车出发____后被乙车追上.
(2) 甲车与乙车在距离地多远处迎面相遇?
(3) 当甲车从地返回的速度满足什么条件时,才能比乙车先回到地?
题型六 一次函数的综合
例6 [2024长沙模拟]如图①,在平面直角坐标系中,正方形的边在轴上,是的中点,直线过定点,交轴于点.
(1) 求点的坐标.
(2) 如图②,当时,过点作,交于点,在直线上是否存在点,使得是等腰直角三角形?若存在,请求出所有满足条件的点;若不存在,请说明理由.
(3) 点在直线上,且,连接,为的中点,连接.求线段的长度的最大值,并直接写出此时点的坐标.
变式跟进
6.[2024娄底模拟]如图①,在平面直角坐标系中,一次函数的图象分别交轴、轴于点,,一次函数的图象经过点,并与轴交于点,是直线上的一个动点.
(1) 直线的解析式为____________,点的坐标为____________.
(2) 若的面积为18,求点的坐标.
(3) 如图②,在(2)的条件下,当点在轴上方时,过点作轴的垂线,交直线于点是轴上一点,在直线上找一点,使以,,,为顶点的四边形是以为边的平行四边形,请直接写出点的坐标.
过关训练 现复活用
A组·基础达标 逐点击破
1.如果一次函数,是常数的图象不经过第二象限,那么,应满足的条件是( )
A.且 B.且
C.且 D.且
2.[2022仙桃、潜江、天门]如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形.设穿过的时间为,大正方形的面积为,小正方形与大正方形重叠部分的面积为.若,则随变化的函数图象大致为( )
A. B.
C. D.
3.某快递公司每天上午为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量(件)与时间之间的函数图象如图所示,那么当甲、乙两仓库的快递数量相同时,此刻的时间为( )
A.9:15 B.9:20 C.9:25 D.9:30
4.元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”如图是两匹马的行走路程(里)关于行走时间(日)的函数图象,则两图象的交点的坐标是____________________.
5.甲、乙两人参加从A地到B地的长跑比赛,两人在比赛时所跑的路程与时间之间的函数关系如图所示.
请你根据图象,解答下列问题:
(1) __先到达终点(填“甲”或“乙”),甲的速度是____.
(2) 甲与乙何时相遇?
(3) 在甲、乙相遇之前,甲与乙何时相距?
B组·能力提升 强化突破
6.[2024汨罗模拟]如图,在平面直角坐标系中,矩形的边,边,直线与矩形的边和都有交点,交点分别是点,.
(1) 请用含的代数式分别表示点和点的坐标:________________,________________;
(2) 当四边形为平行四边形时,求的值.
7.[2024宁乡模拟]如图,在平面直角坐标系中,直线与直线相交于点,分别交坐标轴于点,,,.
(1) 求和的值;
(2) 如图,是直线上的一个动点,设点的横坐标为,当时,求点的坐标;
(3) 直线上有一点,在平面内找一点,使得以为一边,以,,,为顶点的四边形是菱形,请写出符合条件的点的坐标.
8.[2024湘西州模拟改编]我们不妨约定:在平面直角坐标系中,将点称为“芙蓉点”,经过点的函数,称为“芙蓉函数”.
(1) 有函数:;;.其中函数____(填序号)是“芙蓉函数”.
(2) 已知“芙蓉函数”的图象经过点,求该“芙蓉函数”的解析式.
(3) 若直线与轴、轴分别交于点,,是轴上一点,若将沿直线折叠,点恰好落在轴上的点处.试问经过,两点的一次函数是否可以为“芙蓉函数”?若可以,请直接写出所有函数解析式;若不可以,请说明理由.
9.[2024衡阳模拟]如图,已知矩形的顶点在坐标原点,点,分别在轴、轴的正半轴上,顶点,直线经过点交于点、交轴于点,是的中点,直线交于点.
(1) 求点的坐标及直线的函数解析式.
(2) 求的面积,并在直线上找一点,使,并求出点的坐标.
(3) 在轴上有一点,过点作轴的垂线,分别交直线,于点,,在线段上是否存在一点,使得为等腰直角三角形 若存在,请求出点的坐标;若不存在,请说明理由.
专题4 一次函数
题型归类 举一反三
题型一 函数的概念及图象
【点悟】 解决这类函数图象描述事物变化规律的问题,关键是正确分析事物的变化过程,理解函数图象的横、纵坐标的含义,同时要注意函数自变量的取值范围.
例1 B
变式跟进
1.C
题型二 一次函数的图象与性质
【点悟】 一次函数 的图象和性质与解析式中的系数,有关,如下表:
, , , ,
图象
经过象限 一、二、三 一、三、四 一、二、四 二、三、四
增减性 随 的增大而增大 随 的增大而增大 随 的增大而减小 随 的增大而减小
例2 B
变式跟进
2.A
题型三 求一次函数的解析式
【点悟】 求一次函数 的解析式时,把已知点的坐标代入解析式,运用待定系数法求出,;求一次函数与坐标轴的交点坐标时,是根据坐标轴的坐标特征代入解析式求出符合题意的解.
例3 (1) 解:由题意,得解得
一次函数的解析式为.
(2) ,
当时,,即.
变式跟进
3.(1) 解:设一次函数的解析式为.
将点,代入,
得解得
一次函数的解析式为.
(2) 将的图象向上平移3个单位长度,
平移后的直线的解析式为.
在中,令,得,
平移后的图象与轴的交点的坐标为.
题型四 一次函数与一元一次不等式(组)、方程(组)
例4
变式跟进
4.
题型五 一次函数的实际应用
例5 (1) 解:设每个甲种粽子的进价为元,则每个乙种粽子的进价为元,
由题意,得,解得.
经检验,是原方程的根,且符合题意,
此时.
答:每个甲种粽子的进价为10元,每个乙种粽子的进价为12元.
(2) ① 设购进甲种粽子个,则购进乙种粽子个,
由题意,得,
关于的函数解析式为.
甲种粽子的数量不低于乙种粽子数量的2倍,
,解得.
的取值范围为,为正整数.
② 由①知,,,为正整数,
随的增大而减小,
当时,有最大值,最大值为,此时(个).
答:当购进甲种粽子134个,乙种粽子66个时,获得利润最大,最大利润为466元.
变式跟进
5.(1) ; 1.5
(2) 解:设乙车从地到地的解析式为,将点,代入,得解得
,
当时,,
设乙车从地到地的解析式为,
将点代入,得
,
解得,
.
当两车迎面相遇时,,
解得,
将代入,得.
答:甲车与乙车在距离地处迎面相遇.
(3) 当乙车返回地时,有,
解得,
甲车要比乙车先回到地,速度要大于.
答:当甲车从地返回的速度大于时,才能比乙车先回到地.
题型六 一次函数的综合
例6 (1) 解:,
,
当时,,
直线过定点,
.
(2) 存在.
当时,直线的函数解析式为.
当时,,
.
正方形的边在轴上,是的中点,,
,,, ,
.
如答图①,过点作交的延长线于点,
例6答图①
则,.
,
,
,
,
,
为等腰直角三角形.
点在直线上,且是等腰直角三角形,
当点与点重合时,满足题意,此时.
当点在点上方,且时,满足题意,即为的中点,
.
综上所述,或.
(3) 如答图②,取点,连接,,则,
例6答图②
为的中点,.
为的中点,
.
,
当,,三点共线,即点在的延长线上时,有最大值为的长,此时的值最大,如答图②.
,
的最大值为,
的最大值为,
此时.
变式跟进
6.(1) ;
(2) 解:设点,
点的坐标为,点的坐标为,
.
,
,
.
当时,;
当时,.
点的坐标为或.
(3) 点在轴上方,
.
当时,,
,
.
设点,则,
,
当时,以,,,为顶点的四边形是以为边的平行四边形,
,
解得或,
当时,,;
当时,,,
点的坐标为或.
过关训练 现复活用
A组·基础达标 逐点击破
1.B 2.A 3.B
4.
5.(1) 乙; 250
(2) 解:设甲跑的路程与时间之间的函数解析式为.
由图象,可得.
设当时,乙跑的路程与时间之间的函数解析式为.
由图象,可得
解得
当时,乙跑的路程与时间之间的函数解析式为.
联立解得
甲与乙在时相遇.
(3) 设甲、乙相遇之前,经过的时间为时,甲与乙相距.
由题意,得或,
解得或.
在甲、乙相遇之前,经过或时甲与乙相距.
B组·能力提升 强化突破
6.(1) ;
(2) 解: 四边形是矩形,,,
,,,
由(1)知,点,的坐标分别为,,
则,.
当四边形为平行四边形时,则,即,
解得.
7.(1) 解:将点代入,得,解得,
点.
将点代入,得,
解得,
,.
(2) 由(1)得直线的解析式为,
点,
,
解得或,
点的坐标是或.
(3) 设点,点.
由(1)知,点,的坐标分别为,,
则.
当是边时,
当点在点的上方时,则,即,
解得,
点或,
此时点在点的正下方5个单位长度,
则点或;
当点在点的下方时,则,不符合题意;
当是对角线时,点,的纵坐标为,则,
解得,则点的横坐标为5,
点的坐标为.
综上所述,点的坐标为或或.
8.(1) ②
(2) 解: “芙蓉函数”的图象经过点,
的图象也经过点,
解得
该“芙蓉函数”的解析式为.
(3) 存在“芙蓉函数”.
9.(1) 解: 四边形为矩形,点的坐标为,
点的坐标为,轴.
直线经过点,
,
,
直线的函数解析式为.
当时,有,
解得,
点的坐标为.
是的中点,
点的坐标为,即,
直线的函数解析式为.
(2)
.
当时,,
点的坐标为.
设点的坐标为.
,
,
解得或,
点的坐标为或.
(3) 点的坐标为,
点的坐标为,点的坐标为.
分三种情况:
①当 时,如答图①所示,
第9题答图①
为等腰直角三角形,
,即,
解得,
,
此时点的坐标为;
②当 时,如答图②所示,
第9题答图②
为等腰直角三角形,
,即,
解得,
,
此时点的坐标为;
③当 时,过点作于点,如答图③所示.
第9题答图③
为等腰直角三角形,
,即或,
解得或,
当时,点的坐标为,点的坐标为,
此时点的坐标为;
当时,点的坐标为,点的坐标为,
此时点的坐标为.
综上所述,在线段上存在一点,使得为等腰直角三角形;点的坐标为或或或.
