专题5 数据的分析(含答案)初中数学人教版八年级下册
文档属性
| 名称 | 专题5 数据的分析(含答案)初中数学人教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 239.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 16:03:43 | ||
图片预览



文档简介
专题5 数据的分析
题型归类 举一反三
题型一 平均数、中位数、众数
例1 在一次数学考试中,某小组的10名学生的成绩如下表:
分数 60 70 80 90 100
人数 1 1 5 2 1
则下列说法正确的是( )
A.学生成绩是80分的频率是 B.学生成绩的中位数是80分
C.学生成绩的众数是5 D.学生成绩的平均数是80分
变式跟进
1.[2024益阳模拟]为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表
组别 A B C D
身高
根据图表提供的信息,解答下列问题:
(1) 抽取的样本中,男生的身高众数在______组,中位数在______组;
(2) 抽取的样本中,女生身高在组的人数有多少人;
(3) 已知该校共有男生840人,女生820人,请估计该校学生身高在C组的人数.
题型二 方差
例2 [2024衡阳模拟]从甲、乙两种饮料中各抽取10盒250毫升的果汁饮料,检查其中的维生素C的含量,所得数据如下(单位:):
甲:120,123,119,121,122,124,119,122,121,119;
乙:121,119,124,119,123,124,123,122,123,122.
通过计算说明哪种饮料维生素C的平均含量高?哪种饮料维生素C的含量比较稳定?
变式跟进
2.甲、乙两名同学分别进行六次射击训练,训练成绩(环)如下表:
第一次 第二次 第三次 第四次 第五次 第六次
甲 9 8 6 7 8 10
乙 8 7 9 7 8 8
关于他们的训练成绩,下列说法正确的是( )
A.他们训练成绩的平均数相同 B.他们训练成绩的中位数不同
C.他们训练成绩的众数不同 D.他们训练成绩的方差不同
3.若一组数据,,的平均数为4,方差为3,则数据,,的平均数和方差分别是( )
A.4,3 B.6,3 C.3,4 D.6,5
题型三 用样本估计总体
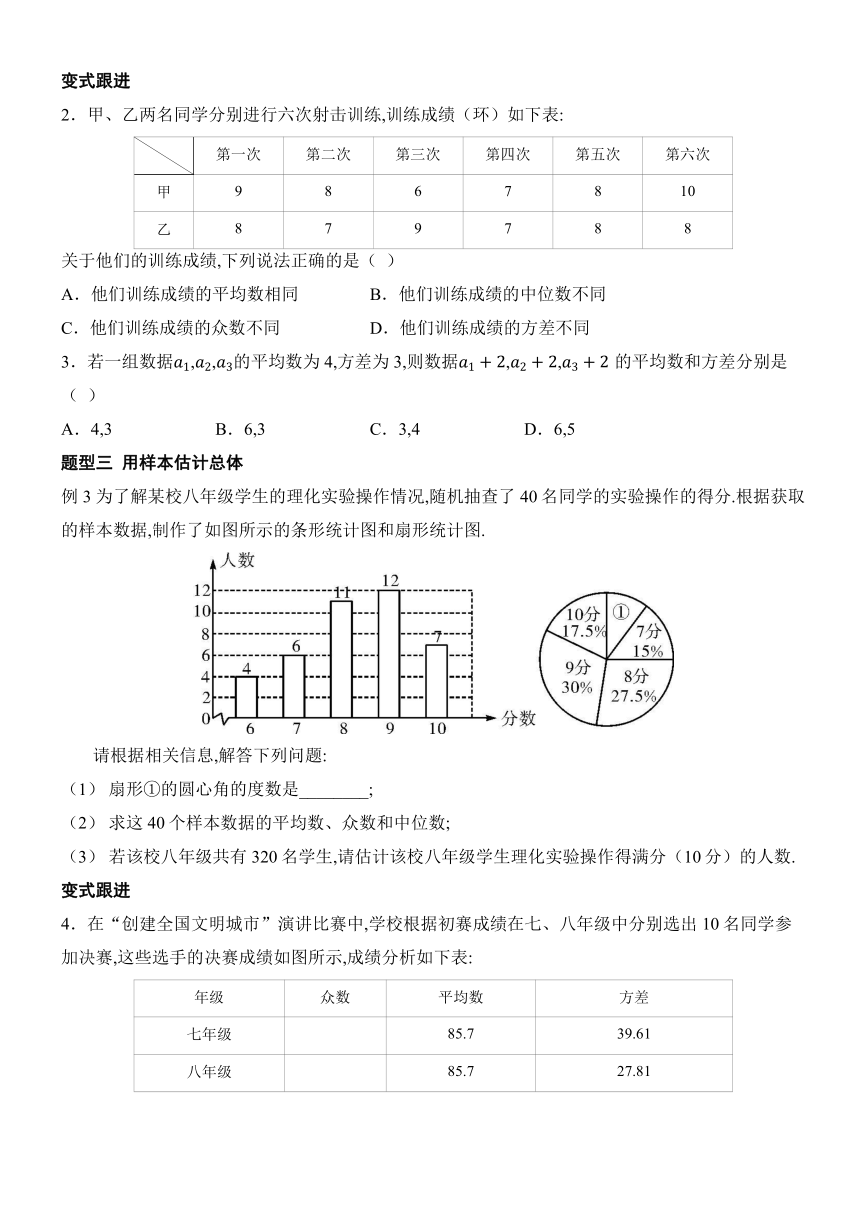
例3 为了解某校八年级学生的理化实验操作情况,随机抽查了40名同学的实验操作的得分.根据获取的样本数据,制作了如图所示的条形统计图和扇形统计图.
请根据相关信息,解答下列问题:
(1) 扇形①的圆心角的度数是________;
(2) 求这40个样本数据的平均数、众数和中位数;
(3) 若该校八年级共有320名学生,请估计该校八年级学生理化实验操作得满分(10分)的人数.
变式跟进
4.在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级中分别选出10名同学参加决赛,这些选手的决赛成绩如图所示,成绩分析如下表:
年级 众数 平均数 方差
七年级 85.7 39.61
八年级 85.7 27.81
根据以上提供的信息,解答下列问题:
(1) 请你把上面的表格填写完整.
(2) 考虑平均数与方差,你认为__年级的团体成绩更好.
(3) 假设在每个年级的决赛选手中分别选出3名参加总决赛,你认为哪个年级的实力更强?请说明理由.
题型四 分析数据进行决策
例4 [2023长沙模拟]某初中举办“课外读物知识竞赛”,八年级和七年级组根据初赛成绩各选出5名选手组成2组代表队参加决赛,两个年级各选出5名选手的决赛成绩如图所示(满分100分):
平均数 中位数 众数 方差
八年级 85
七年级 85 80 100 160
(1) 填空:__,__.
(2) 结合两个年级成绩的平均数和中位数进行分析,哪个年级的决赛成绩较好?
(3) 计算八年级代表队决赛成绩的方差,并判断哪一个代表队选手成绩更为稳定.
变式跟进
5.[2022益阳模拟]八(1)班为了从李明、张亮两名男同学中选拔一人参加全校举行的1分钟跳绳比赛,现对他们进行了训练测试,他们10次测试的成绩如下(单位:次):
李明:186,191,196,191,186,201,196,196,211,206;
张亮:171,186,182,191,201,197,201,205,211,215.
为了比较两人的成绩,制作了如下统计分析表:
平均数 中位数 众数 方差
李明 196 196
张亮 196 201 166.4
(1) 填空:____,____;
(2) 求出李明成绩的方差的值;
(3) 请选择合适的统计量作为选拔标准,说明应选拔哪名同学参加全校举行的跳绳比赛.
过关训练 现复活用
A组·基础达标 逐点击破
1.[2022自贡]六名同学的年龄(单位:岁)分别是:13,14,15,14,14,15.关于这组数据,正确的说法是( )
A.平均数是14 B.中位数是14.5
C.方差是3 D.众数是14
2.如果一组数据6,7,,9,5的平均数是,那么这组数据的中位数为( )
A.5 B.6 C.7 D.9
3.[2024长沙模拟]2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如图所示的两幅统计图.
请根据图中提供的信息,解答下面的问题:
(1) 扇形统计图中的__,本次调查数据的中位数是____,众数是____.
(2) 该校此次抽查的这些学生一周平均的课外劳动时间是多少?
(3) 若该校共有2 000名学生,请估计该校学生一周的课外劳动时间不小于的人数.
4.[2024娄底模拟]某校舞蹈队共12名学生,测量并获取了所有学生的身高(单位:),数据整理如下:
名学生的身高:
160,162,164,165,165,165,166,167,168,168,170,172;
名学生的身高的平均数、中位数、众数如下表:
平均数 中位数 众数
166
(1) 表中______,____;
(2) 对于不同组的学生,如果一组学生的身高的方差越小,那么认为该组舞台呈现效果越好,据此推断:在下表两组学生中,舞台呈现效果更好的是____(填“甲组”或“乙组”);
甲组学生的身高 162 165 165 166 166
乙组学生的身高 160 162 164 165 172
(3) 该舞蹈队要选五名学生参加比赛,已确定三名学生参赛,他们的身高(单位:)分别为168,168,172,他们的身高的方差为.在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为________.
B组·能力提升 强化突破
5.[2024常德模拟]李明为了了解某品牌新能源乘用车的发展情况,从该品牌汽车官方网站收集到以下信息:
2024年1月该品牌各级别新能源乘用车 的平均销售单价统计表
乘用车级别 微型 小型 紧凑型 中型 大型 超大型
平均单价/万元 8 10 15 20 30 50
根据所给的图表,解答下列问题:
(1) 2024年1月与2023年1月相比,增长率最低的新能源乘用车级别是____.
(2) 2024年1月该品牌所有销售的新能源乘用车平均单价是多少万元?(结果保留两位小数)
(3) 该品牌汽车想通过调整投产计划以满足市场需求,如果你是李明,你如何运用所学的统计学知识向该品牌车企提出后续投产规划的合理建议?
专题5 数据的分析
题型归类 举一反三
题型一 平均数、中位数、众数
例1 B
变式跟进
1.(1) B; C
(2) 解:女生身高在组的百分比为.
抽取的样本中,男生的人数为.
抽取的样本中,男生、女生的人数相同,
抽取的样本中,女生身高在组的人数为.
(3)
(人),
估计该校学生身高在C组的人数为415.
题型二 方差
例2 解:,
,
乙种饮料维生素C的平均含量高.
又,
,
,
甲种饮料维生素C的含量较稳定.
变式跟进
2.D 3.B
题型三 用样本估计总体
【点悟】 用样本估计总体是统计的核心思想.具体的有用样本平均数估计总体平均数、用样本百分率估计总体百分率、用样本方差估计总体方差等.
例3 (1)
(2) 解:,
平均数是8.3分.
分出现了12次,出现的次数最多,
众数是9分.
将这40个数据按从小到大的顺序排列,第20,21个数都是8分,
中位数是(分).
(3) (名).
答:估计该校八年级学生理化实验操作得满分(10分)的人数为56.
变式跟进
4.(1) 80; 85
(2) 八
(3) 解:我认为七年级的实力更强.理由如下:
七年级前三名的总分为(分),
八年级前三名的总分为(分),
七年级的实力更强.
题型四 分析数据进行决策
例4 (1) 85; 85
(2) 解:两个年级的平均成绩相同,而八年级的中位数较大,因而八年级的决赛成绩较好.
(3) 八年级决赛成绩的方差.
八年级决赛成绩的方差是70,七年级决赛成绩的方差是160,,
八年级代表队选手的成绩更为稳定.
变式跟进
5.(1) 196; 199
(2) 解:李明成绩的方差.
(3) 从方差来看,李明成绩的方差小于张亮成绩的方差,说明李明的成绩比张亮的成绩稳定,可选拔李明参加全校举行的跳绳比赛.
或从中位数来看,李明成绩的中位数为196,张亮成绩的中位数为199,张亮成绩在201次及以上次数比较多,说明张亮比李明的成绩在201次及以上次数机会要大,可选拔张亮参加全校举行的跳绳比赛 (答案不唯一,合理即可).
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.B
3.(1) 25; 3; 3
(2) 解:此次抽查的这些学生一周平均的课外劳动时间是.
答:此次抽查的这些学生一周平均的课外劳动时间是.
(3) (名).
答:估计该校学生一周的课外劳动时间不小于的人数为1 400.
4.(1) 165.5; 165
(2) 甲组
(3) 167,170
B组·能力提升 强化突破
5.(1) 大型
(2) 解:
(万元).
答:2024年1月该品牌所有销售的新能源乘用车的平均单价约是16.72万元.
(3) 从条形统计图可知,2024年1月销售数据中,销售量最大的车型为紧凑型车;从条形统计图来看增长率最高的车型是紧凑型车,所以建议多生产紧凑型车.
题型归类 举一反三
题型一 平均数、中位数、众数
例1 在一次数学考试中,某小组的10名学生的成绩如下表:
分数 60 70 80 90 100
人数 1 1 5 2 1
则下列说法正确的是( )
A.学生成绩是80分的频率是 B.学生成绩的中位数是80分
C.学生成绩的众数是5 D.学生成绩的平均数是80分
变式跟进
1.[2024益阳模拟]为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表
组别 A B C D
身高
根据图表提供的信息,解答下列问题:
(1) 抽取的样本中,男生的身高众数在______组,中位数在______组;
(2) 抽取的样本中,女生身高在组的人数有多少人;
(3) 已知该校共有男生840人,女生820人,请估计该校学生身高在C组的人数.
题型二 方差
例2 [2024衡阳模拟]从甲、乙两种饮料中各抽取10盒250毫升的果汁饮料,检查其中的维生素C的含量,所得数据如下(单位:):
甲:120,123,119,121,122,124,119,122,121,119;
乙:121,119,124,119,123,124,123,122,123,122.
通过计算说明哪种饮料维生素C的平均含量高?哪种饮料维生素C的含量比较稳定?
变式跟进
2.甲、乙两名同学分别进行六次射击训练,训练成绩(环)如下表:
第一次 第二次 第三次 第四次 第五次 第六次
甲 9 8 6 7 8 10
乙 8 7 9 7 8 8
关于他们的训练成绩,下列说法正确的是( )
A.他们训练成绩的平均数相同 B.他们训练成绩的中位数不同
C.他们训练成绩的众数不同 D.他们训练成绩的方差不同
3.若一组数据,,的平均数为4,方差为3,则数据,,的平均数和方差分别是( )
A.4,3 B.6,3 C.3,4 D.6,5
题型三 用样本估计总体
例3 为了解某校八年级学生的理化实验操作情况,随机抽查了40名同学的实验操作的得分.根据获取的样本数据,制作了如图所示的条形统计图和扇形统计图.
请根据相关信息,解答下列问题:
(1) 扇形①的圆心角的度数是________;
(2) 求这40个样本数据的平均数、众数和中位数;
(3) 若该校八年级共有320名学生,请估计该校八年级学生理化实验操作得满分(10分)的人数.
变式跟进
4.在“创建全国文明城市”演讲比赛中,学校根据初赛成绩在七、八年级中分别选出10名同学参加决赛,这些选手的决赛成绩如图所示,成绩分析如下表:
年级 众数 平均数 方差
七年级 85.7 39.61
八年级 85.7 27.81
根据以上提供的信息,解答下列问题:
(1) 请你把上面的表格填写完整.
(2) 考虑平均数与方差,你认为__年级的团体成绩更好.
(3) 假设在每个年级的决赛选手中分别选出3名参加总决赛,你认为哪个年级的实力更强?请说明理由.
题型四 分析数据进行决策
例4 [2023长沙模拟]某初中举办“课外读物知识竞赛”,八年级和七年级组根据初赛成绩各选出5名选手组成2组代表队参加决赛,两个年级各选出5名选手的决赛成绩如图所示(满分100分):
平均数 中位数 众数 方差
八年级 85
七年级 85 80 100 160
(1) 填空:__,__.
(2) 结合两个年级成绩的平均数和中位数进行分析,哪个年级的决赛成绩较好?
(3) 计算八年级代表队决赛成绩的方差,并判断哪一个代表队选手成绩更为稳定.
变式跟进
5.[2022益阳模拟]八(1)班为了从李明、张亮两名男同学中选拔一人参加全校举行的1分钟跳绳比赛,现对他们进行了训练测试,他们10次测试的成绩如下(单位:次):
李明:186,191,196,191,186,201,196,196,211,206;
张亮:171,186,182,191,201,197,201,205,211,215.
为了比较两人的成绩,制作了如下统计分析表:
平均数 中位数 众数 方差
李明 196 196
张亮 196 201 166.4
(1) 填空:____,____;
(2) 求出李明成绩的方差的值;
(3) 请选择合适的统计量作为选拔标准,说明应选拔哪名同学参加全校举行的跳绳比赛.
过关训练 现复活用
A组·基础达标 逐点击破
1.[2022自贡]六名同学的年龄(单位:岁)分别是:13,14,15,14,14,15.关于这组数据,正确的说法是( )
A.平均数是14 B.中位数是14.5
C.方差是3 D.众数是14
2.如果一组数据6,7,,9,5的平均数是,那么这组数据的中位数为( )
A.5 B.6 C.7 D.9
3.[2024长沙模拟]2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如图所示的两幅统计图.
请根据图中提供的信息,解答下面的问题:
(1) 扇形统计图中的__,本次调查数据的中位数是____,众数是____.
(2) 该校此次抽查的这些学生一周平均的课外劳动时间是多少?
(3) 若该校共有2 000名学生,请估计该校学生一周的课外劳动时间不小于的人数.
4.[2024娄底模拟]某校舞蹈队共12名学生,测量并获取了所有学生的身高(单位:),数据整理如下:
名学生的身高:
160,162,164,165,165,165,166,167,168,168,170,172;
名学生的身高的平均数、中位数、众数如下表:
平均数 中位数 众数
166
(1) 表中______,____;
(2) 对于不同组的学生,如果一组学生的身高的方差越小,那么认为该组舞台呈现效果越好,据此推断:在下表两组学生中,舞台呈现效果更好的是____(填“甲组”或“乙组”);
甲组学生的身高 162 165 165 166 166
乙组学生的身高 160 162 164 165 172
(3) 该舞蹈队要选五名学生参加比赛,已确定三名学生参赛,他们的身高(单位:)分别为168,168,172,他们的身高的方差为.在选另外两名学生时,首先要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的方差小于,其次要求所选的两名学生与已确定的三名学生所组成的五名学生的身高的平均数尽可能大,则选出的另外两名学生的身高分别为________.
B组·能力提升 强化突破
5.[2024常德模拟]李明为了了解某品牌新能源乘用车的发展情况,从该品牌汽车官方网站收集到以下信息:
2024年1月该品牌各级别新能源乘用车 的平均销售单价统计表
乘用车级别 微型 小型 紧凑型 中型 大型 超大型
平均单价/万元 8 10 15 20 30 50
根据所给的图表,解答下列问题:
(1) 2024年1月与2023年1月相比,增长率最低的新能源乘用车级别是____.
(2) 2024年1月该品牌所有销售的新能源乘用车平均单价是多少万元?(结果保留两位小数)
(3) 该品牌汽车想通过调整投产计划以满足市场需求,如果你是李明,你如何运用所学的统计学知识向该品牌车企提出后续投产规划的合理建议?
专题5 数据的分析
题型归类 举一反三
题型一 平均数、中位数、众数
例1 B
变式跟进
1.(1) B; C
(2) 解:女生身高在组的百分比为.
抽取的样本中,男生的人数为.
抽取的样本中,男生、女生的人数相同,
抽取的样本中,女生身高在组的人数为.
(3)
(人),
估计该校学生身高在C组的人数为415.
题型二 方差
例2 解:,
,
乙种饮料维生素C的平均含量高.
又,
,
,
甲种饮料维生素C的含量较稳定.
变式跟进
2.D 3.B
题型三 用样本估计总体
【点悟】 用样本估计总体是统计的核心思想.具体的有用样本平均数估计总体平均数、用样本百分率估计总体百分率、用样本方差估计总体方差等.
例3 (1)
(2) 解:,
平均数是8.3分.
分出现了12次,出现的次数最多,
众数是9分.
将这40个数据按从小到大的顺序排列,第20,21个数都是8分,
中位数是(分).
(3) (名).
答:估计该校八年级学生理化实验操作得满分(10分)的人数为56.
变式跟进
4.(1) 80; 85
(2) 八
(3) 解:我认为七年级的实力更强.理由如下:
七年级前三名的总分为(分),
八年级前三名的总分为(分),
七年级的实力更强.
题型四 分析数据进行决策
例4 (1) 85; 85
(2) 解:两个年级的平均成绩相同,而八年级的中位数较大,因而八年级的决赛成绩较好.
(3) 八年级决赛成绩的方差.
八年级决赛成绩的方差是70,七年级决赛成绩的方差是160,,
八年级代表队选手的成绩更为稳定.
变式跟进
5.(1) 196; 199
(2) 解:李明成绩的方差.
(3) 从方差来看,李明成绩的方差小于张亮成绩的方差,说明李明的成绩比张亮的成绩稳定,可选拔李明参加全校举行的跳绳比赛.
或从中位数来看,李明成绩的中位数为196,张亮成绩的中位数为199,张亮成绩在201次及以上次数比较多,说明张亮比李明的成绩在201次及以上次数机会要大,可选拔张亮参加全校举行的跳绳比赛 (答案不唯一,合理即可).
过关训练 现复活用
A组·基础达标 逐点击破
1.D 2.B
3.(1) 25; 3; 3
(2) 解:此次抽查的这些学生一周平均的课外劳动时间是.
答:此次抽查的这些学生一周平均的课外劳动时间是.
(3) (名).
答:估计该校学生一周的课外劳动时间不小于的人数为1 400.
4.(1) 165.5; 165
(2) 甲组
(3) 167,170
B组·能力提升 强化突破
5.(1) 大型
(2) 解:
(万元).
答:2024年1月该品牌所有销售的新能源乘用车的平均单价约是16.72万元.
(3) 从条形统计图可知,2024年1月销售数据中,销售量最大的车型为紧凑型车;从条形统计图来看增长率最高的车型是紧凑型车,所以建议多生产紧凑型车.
