2024--2025学年人教版九年级数学上册第二十二章 二次函数 综合测试(含答案)
文档属性
| 名称 | 2024--2025学年人教版九年级数学上册第二十二章 二次函数 综合测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 352.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-10 00:00:00 | ||
图片预览



文档简介
第二十二章 二次函数 综合测试 2024--2025学年人教版九年级数学上册
一、单选题(共10题;共30分)
1.(3分)二次函数的图象与y轴的交点坐标是( )
A. B. C. D.
2.(3分)把抛物线先向左平移个单位再向上平移个单位,所得到抛物线的表达式为( )
A. B. C. D.
3.(3分)已知二次函数y=﹣x2+2x+1图象上的三点A(﹣1,y1),B(2,y2),C(4,y3),则y1、y2、y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y1<y2
4.(3分)如图,某涵洞的截面是抛物线形,现测得水面宽AB=1.6m,涵洞顶点O与水面的距离CO是2m,则当水位上升1.5m时,水面的宽度为( )
A.1m B.0.8m C.0.6m D.0.4m
5.(3分)在平面直角坐标系中,将二次函数的图像向左平移2个单位,再向下平移2个单位,平移后的解析式是( )
A. B.
C. D.
6.(3分)若函数的图象与x轴只有一个交点,则m的值为( )
A.0 B.1或9 C.或 D.0或或
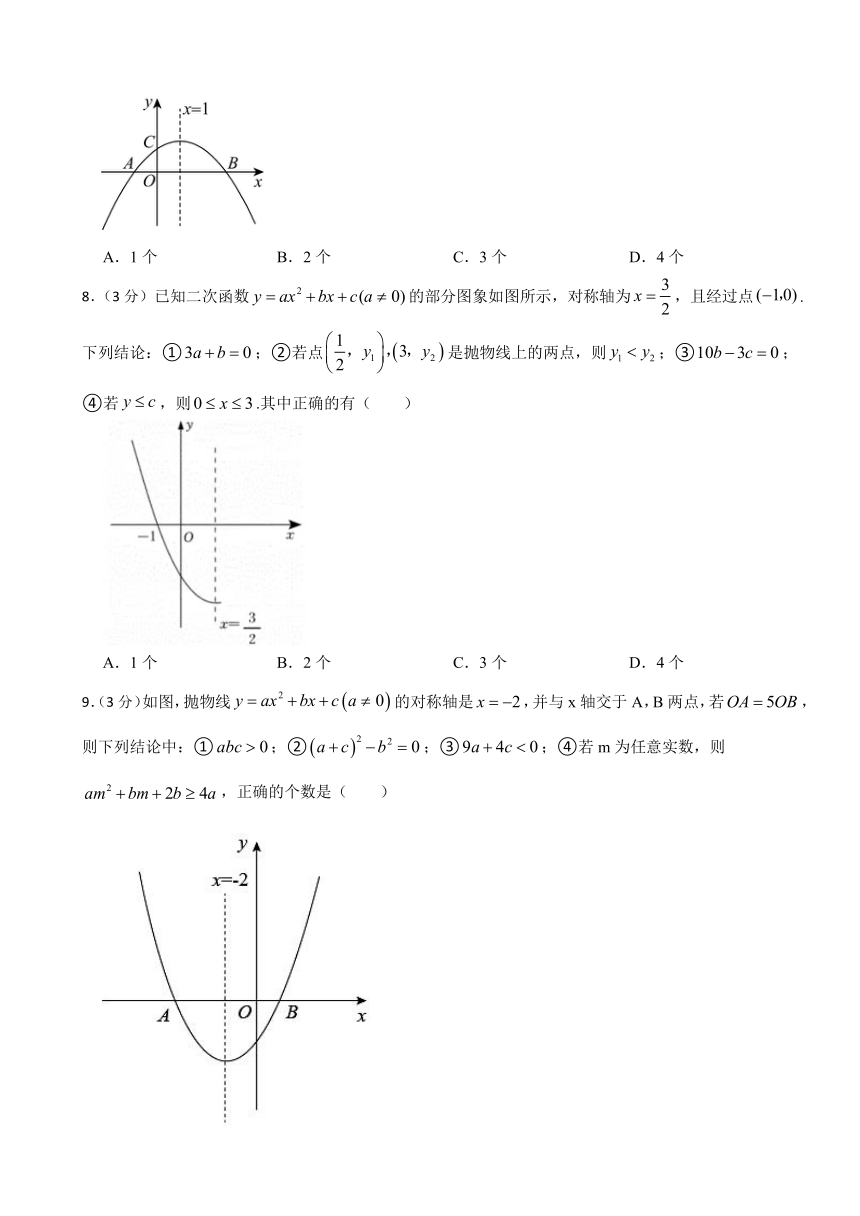
7.(3分)如图所示,已知二次函数的图象与轴交于两点,与轴交于点,,对称轴为直线,则下列结论:①;②;③;④是关于的一元二次方程的一个根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)已知二次函数的部分图象如图所示,对称轴为,且经过点.下列结论:①;②若点是抛物线上的两点,则;③;④若,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.(3分)如图,抛物线的对称轴是,并与x轴交于A,B两点,若,则下列结论中:①;②;③;④若m为任意实数,则,正确的个数是( )
A.1 B.2 C.3 D.4
10.(3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac>0;④a-b+c>0;⑤3a+c<0.正确的个数是( ) .
A.2 B.3 C.4 D.5
二、填空题(共7题;共21分)
11.(3分)已知抛物线如图所示,那么点在第 象限.
12.(3分)请写出一个开口向下,经过原点的二次函数的表达式 .
13.(3分)二次函数 化为 的形式
14.(3分)把抛物线向右平移3个单位长度,再向下平移2个单位长度,所得图象的函数表达式为,则 , .
15.(3分)若抛物线y=x2﹣4x+m与直线y=kx﹣13(k≠0)交于点(2,﹣9),则关于x的方程x2﹣4x+m=k(x﹣1)﹣11的解为 .
16.(3分)已知二次函数 ,它的图象与x轴的交点坐标为 .
17.(3分)如图1,E是正方形ABCD的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作正方形AEFG,连接CF.已知的面积(S)与BE的长(x)之间的函数关系如图2所示,若该抛物线顶点P的纵坐标为8,则正方形ABCD的边长为 .
三、解答题(共6题;共49分)
18.(6分)某农场准备围建一个矩形养鸡场,其中一边靠墙(墙的长度为15米),其余部分用篱笆围成,在墙所对的边留一道1米宽的门,已知篱笆的总长度为23米.求整个鸡场的总面积的最大值.
19.(6分)已知二次函数的图象经过点.
(1)(3分)试确定此二次函数的解析式;
(2)(3分)请你判断点是否在这个二次函数的图象上?
20.(9分)如图①,皮皮燃放一种手持烟花,这种烟花每隔发射一发花弹,每一发花弹的飞行路径、爆炸时的高度均相同.皮皮发射出的第一发花弹的飞行高度与飞行时间之间的函数关系如图②所示.
(1)(3分)求皮皮发射出的第一发花弹的飞行高度关于飞行时间的函数表达式.
(2)(3分)第一发花弹发射后,第二发花弹达到的高度为多少米
(3)(3分)为了安全,要求花弹爆炸时的高度不低于.皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,请通过计算说明花弹的爆炸高度是否符合安全要求.
21.(9分)百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,减少库存,经市场调查发现:如果每件童装降价1元,那么平均每天可多售出2件.
(1)(4分)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
(2)(5分)若设每件童装降价元时,平均每天销售这种童装盈利元,求与的函数关系式,并求的最大值.
22.(9分)约定:为函数的“关联数”,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”.若关联数为的函数图象与x轴有两个整交点(m为正整数),求这个函数图象上整交点的坐标.
23.(10分)如图1,抛物线经过点,,并交x轴于点E,F(点F在点E的右边).
(1)(5分)求该抛物线的函数表达式.
(2)(5分)如图2,为y轴上一动点,点D的坐标为,过三点P,E,F作抛物线,连接.
①当抛物线的顶点落在线段上时,求此时t的值.
②当抛物线与线段只有一个交点时,直接写出t的取值范围.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】二
12.【答案】答案不唯一( ,任何a<0,c=0的二次函数均可)
13.【答案】
14.【答案】4;8
15.【答案】x1=2,x2=4
16.【答案】(5,0),(-1,0)
17.【答案】8
18.【答案】整个鸡场的总面积的最大值为72平方米.
19.【答案】(1)
(2)点在这个二次函数的图象上
20.【答案】(1)解:由图象可知,抛物线的顶点坐标为(3,19.8),
∴设解析式为:h=a(t-3)2+19.8(a≠0),
把点(0,1.8)代入得:1.8=a(0-3)2+ 19.8,
∴a =-2,
∴h=-2(t-3)2+ 19.8,
∴函数解析式为:h=-2(t-3)2+ 19.8
(2)解:当第一发花弹发射3秒后,第二发花弹发射1秒,
把t=1代入h=-2(t-3)2+ 19.8得,
h=-2(1-3)2+19.8-11.8(米)
(3)解:这种烟花每隔2秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同,
∴皮皮小朋友发射出的第一发花弹的函数解析式为:h=-2(t-3)2 + 19.8,
第二发花弹的抛物线的顶点坐标为(5,19.8)
∴第二发花弹的函数解析式为:h'=-2(t-5)2+ 19.8,
皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,
则令h= h'得-2(t-3)2+19.8=-2(t-5)2 + 19.8
∴t=4秒,此时h= h'=17.8米>16米,
则花弹的爆炸高度符合安全要求
21.【答案】(1)每件童装应降价20元
(2),最大为1250
22.【答案】,,
23.【答案】(1)
(2)①;②t的取值范围为或或.
一、单选题(共10题;共30分)
1.(3分)二次函数的图象与y轴的交点坐标是( )
A. B. C. D.
2.(3分)把抛物线先向左平移个单位再向上平移个单位,所得到抛物线的表达式为( )
A. B. C. D.
3.(3分)已知二次函数y=﹣x2+2x+1图象上的三点A(﹣1,y1),B(2,y2),C(4,y3),则y1、y2、y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y1<y2
4.(3分)如图,某涵洞的截面是抛物线形,现测得水面宽AB=1.6m,涵洞顶点O与水面的距离CO是2m,则当水位上升1.5m时,水面的宽度为( )
A.1m B.0.8m C.0.6m D.0.4m
5.(3分)在平面直角坐标系中,将二次函数的图像向左平移2个单位,再向下平移2个单位,平移后的解析式是( )
A. B.
C. D.
6.(3分)若函数的图象与x轴只有一个交点,则m的值为( )
A.0 B.1或9 C.或 D.0或或
7.(3分)如图所示,已知二次函数的图象与轴交于两点,与轴交于点,,对称轴为直线,则下列结论:①;②;③;④是关于的一元二次方程的一个根.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)已知二次函数的部分图象如图所示,对称轴为,且经过点.下列结论:①;②若点是抛物线上的两点,则;③;④若,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.(3分)如图,抛物线的对称轴是,并与x轴交于A,B两点,若,则下列结论中:①;②;③;④若m为任意实数,则,正确的个数是( )
A.1 B.2 C.3 D.4
10.(3分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac>0;④a-b+c>0;⑤3a+c<0.正确的个数是( ) .
A.2 B.3 C.4 D.5
二、填空题(共7题;共21分)
11.(3分)已知抛物线如图所示,那么点在第 象限.
12.(3分)请写出一个开口向下,经过原点的二次函数的表达式 .
13.(3分)二次函数 化为 的形式
14.(3分)把抛物线向右平移3个单位长度,再向下平移2个单位长度,所得图象的函数表达式为,则 , .
15.(3分)若抛物线y=x2﹣4x+m与直线y=kx﹣13(k≠0)交于点(2,﹣9),则关于x的方程x2﹣4x+m=k(x﹣1)﹣11的解为 .
16.(3分)已知二次函数 ,它的图象与x轴的交点坐标为 .
17.(3分)如图1,E是正方形ABCD的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作正方形AEFG,连接CF.已知的面积(S)与BE的长(x)之间的函数关系如图2所示,若该抛物线顶点P的纵坐标为8,则正方形ABCD的边长为 .
三、解答题(共6题;共49分)
18.(6分)某农场准备围建一个矩形养鸡场,其中一边靠墙(墙的长度为15米),其余部分用篱笆围成,在墙所对的边留一道1米宽的门,已知篱笆的总长度为23米.求整个鸡场的总面积的最大值.
19.(6分)已知二次函数的图象经过点.
(1)(3分)试确定此二次函数的解析式;
(2)(3分)请你判断点是否在这个二次函数的图象上?
20.(9分)如图①,皮皮燃放一种手持烟花,这种烟花每隔发射一发花弹,每一发花弹的飞行路径、爆炸时的高度均相同.皮皮发射出的第一发花弹的飞行高度与飞行时间之间的函数关系如图②所示.
(1)(3分)求皮皮发射出的第一发花弹的飞行高度关于飞行时间的函数表达式.
(2)(3分)第一发花弹发射后,第二发花弹达到的高度为多少米
(3)(3分)为了安全,要求花弹爆炸时的高度不低于.皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,请通过计算说明花弹的爆炸高度是否符合安全要求.
21.(9分)百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,减少库存,经市场调查发现:如果每件童装降价1元,那么平均每天可多售出2件.
(1)(4分)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
(2)(5分)若设每件童装降价元时,平均每天销售这种童装盈利元,求与的函数关系式,并求的最大值.
22.(9分)约定:为函数的“关联数”,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”.若关联数为的函数图象与x轴有两个整交点(m为正整数),求这个函数图象上整交点的坐标.
23.(10分)如图1,抛物线经过点,,并交x轴于点E,F(点F在点E的右边).
(1)(5分)求该抛物线的函数表达式.
(2)(5分)如图2,为y轴上一动点,点D的坐标为,过三点P,E,F作抛物线,连接.
①当抛物线的顶点落在线段上时,求此时t的值.
②当抛物线与线段只有一个交点时,直接写出t的取值范围.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】C
10.【答案】B
11.【答案】二
12.【答案】答案不唯一( ,任何a<0,c=0的二次函数均可)
13.【答案】
14.【答案】4;8
15.【答案】x1=2,x2=4
16.【答案】(5,0),(-1,0)
17.【答案】8
18.【答案】整个鸡场的总面积的最大值为72平方米.
19.【答案】(1)
(2)点在这个二次函数的图象上
20.【答案】(1)解:由图象可知,抛物线的顶点坐标为(3,19.8),
∴设解析式为:h=a(t-3)2+19.8(a≠0),
把点(0,1.8)代入得:1.8=a(0-3)2+ 19.8,
∴a =-2,
∴h=-2(t-3)2+ 19.8,
∴函数解析式为:h=-2(t-3)2+ 19.8
(2)解:当第一发花弹发射3秒后,第二发花弹发射1秒,
把t=1代入h=-2(t-3)2+ 19.8得,
h=-2(1-3)2+19.8-11.8(米)
(3)解:这种烟花每隔2秒发射一发花弹,每一发花弹的飞行路径,爆炸时的高度均相同,
∴皮皮小朋友发射出的第一发花弹的函数解析式为:h=-2(t-3)2 + 19.8,
第二发花弹的抛物线的顶点坐标为(5,19.8)
∴第二发花弹的函数解析式为:h'=-2(t-5)2+ 19.8,
皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,
则令h= h'得-2(t-3)2+19.8=-2(t-5)2 + 19.8
∴t=4秒,此时h= h'=17.8米>16米,
则花弹的爆炸高度符合安全要求
21.【答案】(1)每件童装应降价20元
(2),最大为1250
22.【答案】,,
23.【答案】(1)
(2)①;②t的取值范围为或或.
同课章节目录
