2024--2025学年人教版九年级数学上册第二十三章旋转综合测试(含答案)
文档属性
| 名称 | 2024--2025学年人教版九年级数学上册第二十三章旋转综合测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 522.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-10 16:44:12 | ||
图片预览



文档简介
第二十三章 旋转 综合测试 2024--2025学年人教版九年级数学上册
一、单选题(共10题;共30分)
1.(3分)如图所示,在中,,将绕点逆时针旋转得到,点的对应点分别为,连接.当点在同一条直线上时,则旋转角的度数是( )
A. B. C. D.
2.(3分)点关于原点对称的点的坐标是( )
A. B. C. D.
3.(3分)在平面直角坐标系中,将直线l1:y=2x-4平移后,得到的直线l2与l1关于坐标原点成中心对称,则下列平移作法正确的是( )
A.将l1向左平移4个单位长度 B.将l1向左平移8个单位长度
C.将l1向上平移6个单位长度 D.将l1向上平移4个单位长度
4.(3分)八卦脑景区风力发电机(图①)既可以在风力作用下发电,也是景区的一道靓丽风景线.转子叶片图案(图②)绕中心旋转后能与原来的图案重合,那么的值可能是( )
A.45 B.60 C.90 D.120
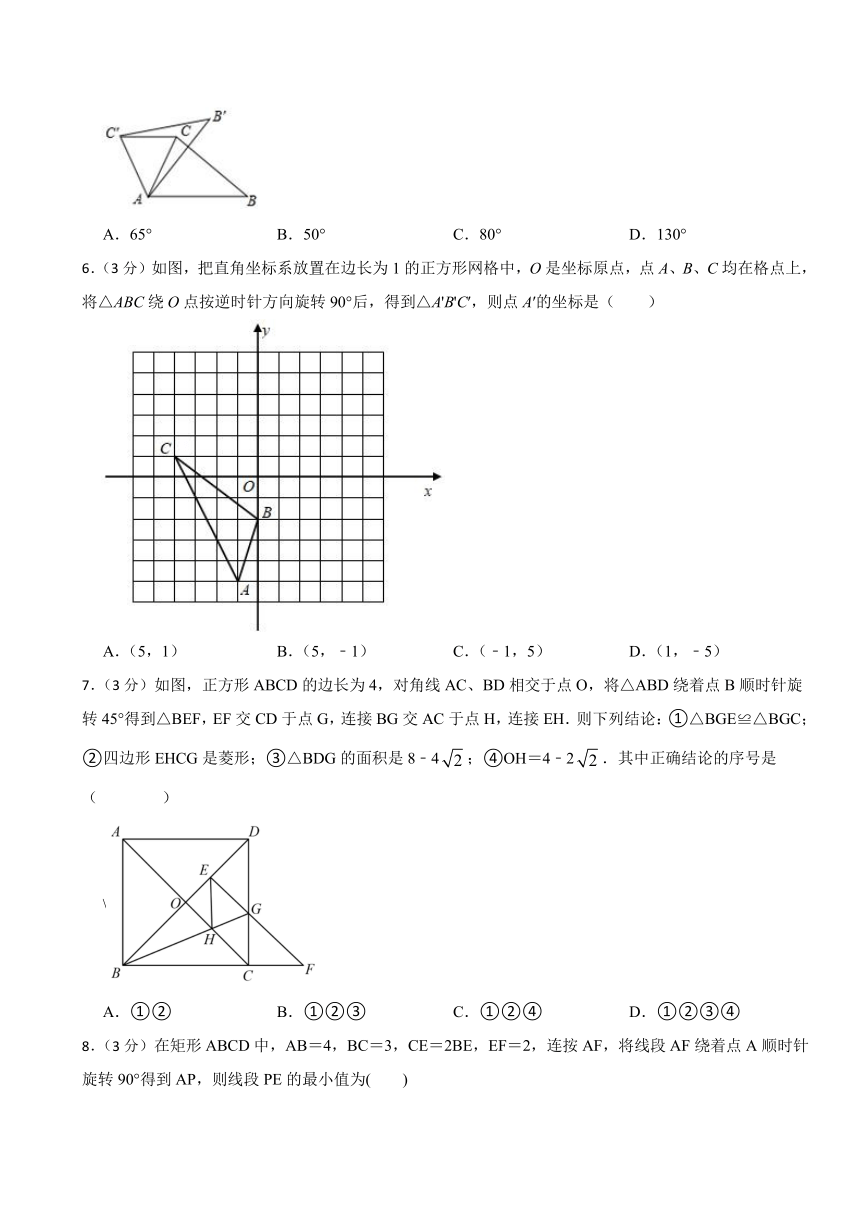
5.(3分)如图,在△ABC中,∠BAC=65°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'的度数为( )
A.65° B.50° C.80° D.130°
6.(3分)如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按逆时针方向旋转90°后,得到△A'B'C′,则点A′的坐标是( )
A.(5,1) B.(5,﹣1) C.(﹣1,5) D.(1,﹣5)
7.(3分)如图,正方形ABCD的边长为4,对角线AC、BD相交于点O,将△ABD绕着点B顺时针旋转45°得到△BEF,EF交CD于点G,连接BG交AC于点H,连接EH.则下列结论:①△BGE≌△BGC;②四边形EHCG是菱形;③△BDG的面积是8﹣4;④OH=4﹣2.其中正确结论的序号是( )
\
A.①② B.①②③ C.①②④ D.①②③④
8.(3分)在矩形ABCD中,AB=4,BC=3,CE=2BE,EF=2,连按AF,将线段AF绕着点A顺时针旋转90°得到AP,则线段PE的最小值为( )
A. B. C.4 D.
9.(3分)如图,矩形ABCD中,AB=2 ,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )
A.4 +3 B.2 C.2 +6 D.4
10.(3分)如图,矩形ABCD被分割成4个直角三角形和1个小矩形后仍是中心对称图形.设上下两个直角三角形的面积都为S1,左右两个直角三角形的面积都为S2,中间小矩形的面积为S3,若对角线EF∥BC,则矩形ABCD的面积一定可以表示为( )
A.4S1 B.8S2 C.8S3 D.2S1+4S3
二、填空题(共7题;共21分)
11.(3分)已知点与点关于原点对称,则 .
12.(3分)点A(-2,3)与点B(a,b)关于坐标原点对称,则的值为 .
13.(3分)如图,在中,,将绕点A逆时针旋转得到,使得点D落在上,若,则的大小为
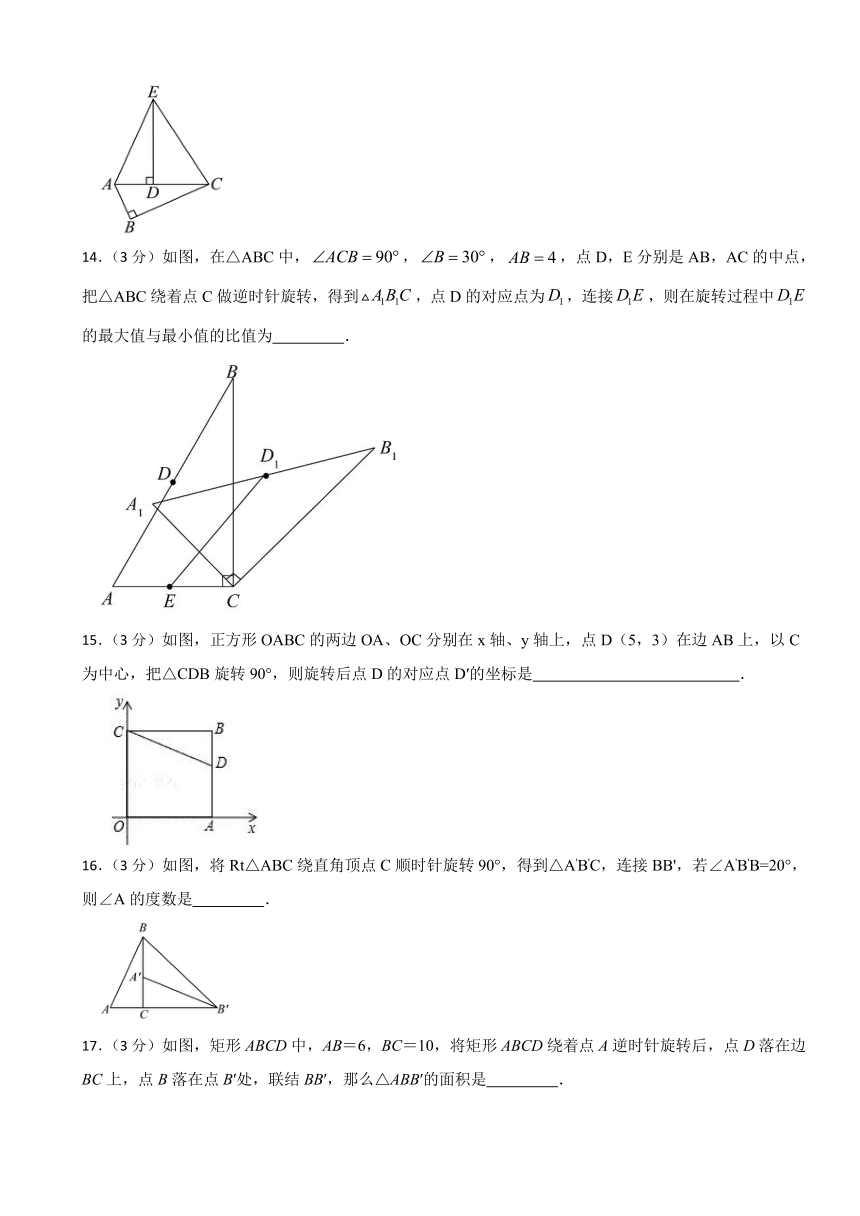
14.(3分)如图,在△ABC中,,,,点D,E分别是AB,AC的中点,把△ABC绕着点C做逆时针旋转,得到,点D的对应点为,连接,则在旋转过程中的最大值与最小值的比值为 .
15.(3分)如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
16.(3分)如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接BB',若∠A'B'B=20°,则∠A的度数是 .
17.(3分)如图,矩形ABCD中,AB=6,BC=10,将矩形ABCD绕着点A逆时针旋转后,点D落在边BC上,点B落在点B′处,联结BB′,那么△ABB′的面积是 .
三、解答题(共7题;共49分)
18.(6分)如图,在中,,,,逆时针旋转一定角度后与重合,且点C恰好成为的中点.
(1)(3分)旋转中心为点 ,并求出旋转角= 度;
(2)(3分)求出的度数和的长.
19.(6分)如图,D是的边延长线上一点,连接,把绕点A顺时针旋转恰好得到,其中D,E是对应点,若,求的度数.
20.(7分) 如图,P是正方形内一点,绕着点B旋转后能到达的位置,若.求线段的长.
21.(7分)在矩形中,,,以点为旋转中心,按逆时针方向旋转矩形得到矩形,旋转角为.
(1)(2分)如图①,当点落在边上时,线段的长度为________;
(2)(2分)如图②,连接,当点落在线段上时,与相交于点,连接,求线段的长度;
(3)(3分)如图③,设点为边的中点,连接、、,在矩形旋转的过程中,求面积的最大值.
22.(7分)如图,在中,,将绕点逆时针旋转得到,点的对应点恰好落在斜边上,连接,已知.
(1)(3分)直接写出的长;
(2)(4分)求的长.
23.(8分)如图1,已知二次函数,与x轴相交于点,点为对称轴上的点,将线段绕点P逆时针旋转,得到线段,且点B在抛物线上.
(1)(4分)求抛物线的解析式;
(2)(4分)如图2,将该二次函数在x轴上方的图象沿x轴翻折到下方,图象的其余部分不变,得到一个新函数图象,当直线与新图象有3个交点时,求m的值.
24.(8分)如图,在直角坐标系中,点的坐标为,连结,将线段绕原点顺时针旋转,得到线段.
(1)(2分)求点的坐标;
(2)(2分)求经过三点的抛物线的解析式;
(3)(2分)在(2)中抛物线的对称轴上是否存在点,使周长最小 若存在,求点出的坐标和的周长;若不存在,请说明理由;
(4)(2分)如果点是(2)中的抛物线上的动点,那么是否存在点使得的面积为:;若有,求出此时点的横坐标;若没有,请说明理由.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】5
12.【答案】9
13.【答案】
14.【答案】3
15.【答案】(2,10)或(﹣2,0)
16.【答案】65°
17.【答案】
18.【答案】(1)A;130
(2),
19.【答案】
20.【答案】解:∵正方形,
∴,
∵绕着点B旋转后能到达的位置,
∴,
∴.
21.【答案】(1)
(2)
(3)
22.【答案】(1)解:将绕点逆时针旋转得到,∴,
∴,,
∴的长为
(2)解:在中,,,由勾股定理得:,
由(1)可知,,
∴,,,
∴,
在中,根据勾股定理得:,
∴的长为
23.【答案】(1)
(2)或
24.【答案】(1);
(2);
(3),
(4)的横坐标为或.
一、单选题(共10题;共30分)
1.(3分)如图所示,在中,,将绕点逆时针旋转得到,点的对应点分别为,连接.当点在同一条直线上时,则旋转角的度数是( )
A. B. C. D.
2.(3分)点关于原点对称的点的坐标是( )
A. B. C. D.
3.(3分)在平面直角坐标系中,将直线l1:y=2x-4平移后,得到的直线l2与l1关于坐标原点成中心对称,则下列平移作法正确的是( )
A.将l1向左平移4个单位长度 B.将l1向左平移8个单位长度
C.将l1向上平移6个单位长度 D.将l1向上平移4个单位长度
4.(3分)八卦脑景区风力发电机(图①)既可以在风力作用下发电,也是景区的一道靓丽风景线.转子叶片图案(图②)绕中心旋转后能与原来的图案重合,那么的值可能是( )
A.45 B.60 C.90 D.120
5.(3分)如图,在△ABC中,∠BAC=65°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'的度数为( )
A.65° B.50° C.80° D.130°
6.(3分)如图,把直角坐标系放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按逆时针方向旋转90°后,得到△A'B'C′,则点A′的坐标是( )
A.(5,1) B.(5,﹣1) C.(﹣1,5) D.(1,﹣5)
7.(3分)如图,正方形ABCD的边长为4,对角线AC、BD相交于点O,将△ABD绕着点B顺时针旋转45°得到△BEF,EF交CD于点G,连接BG交AC于点H,连接EH.则下列结论:①△BGE≌△BGC;②四边形EHCG是菱形;③△BDG的面积是8﹣4;④OH=4﹣2.其中正确结论的序号是( )
\
A.①② B.①②③ C.①②④ D.①②③④
8.(3分)在矩形ABCD中,AB=4,BC=3,CE=2BE,EF=2,连按AF,将线段AF绕着点A顺时针旋转90°得到AP,则线段PE的最小值为( )
A. B. C.4 D.
9.(3分)如图,矩形ABCD中,AB=2 ,BC=6,P为矩形内一点,连接PA,PB,PC,则PA+PB+PC的最小值是( )
A.4 +3 B.2 C.2 +6 D.4
10.(3分)如图,矩形ABCD被分割成4个直角三角形和1个小矩形后仍是中心对称图形.设上下两个直角三角形的面积都为S1,左右两个直角三角形的面积都为S2,中间小矩形的面积为S3,若对角线EF∥BC,则矩形ABCD的面积一定可以表示为( )
A.4S1 B.8S2 C.8S3 D.2S1+4S3
二、填空题(共7题;共21分)
11.(3分)已知点与点关于原点对称,则 .
12.(3分)点A(-2,3)与点B(a,b)关于坐标原点对称,则的值为 .
13.(3分)如图,在中,,将绕点A逆时针旋转得到,使得点D落在上,若,则的大小为
14.(3分)如图,在△ABC中,,,,点D,E分别是AB,AC的中点,把△ABC绕着点C做逆时针旋转,得到,点D的对应点为,连接,则在旋转过程中的最大值与最小值的比值为 .
15.(3分)如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
16.(3分)如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C,连接BB',若∠A'B'B=20°,则∠A的度数是 .
17.(3分)如图,矩形ABCD中,AB=6,BC=10,将矩形ABCD绕着点A逆时针旋转后,点D落在边BC上,点B落在点B′处,联结BB′,那么△ABB′的面积是 .
三、解答题(共7题;共49分)
18.(6分)如图,在中,,,,逆时针旋转一定角度后与重合,且点C恰好成为的中点.
(1)(3分)旋转中心为点 ,并求出旋转角= 度;
(2)(3分)求出的度数和的长.
19.(6分)如图,D是的边延长线上一点,连接,把绕点A顺时针旋转恰好得到,其中D,E是对应点,若,求的度数.
20.(7分) 如图,P是正方形内一点,绕着点B旋转后能到达的位置,若.求线段的长.
21.(7分)在矩形中,,,以点为旋转中心,按逆时针方向旋转矩形得到矩形,旋转角为.
(1)(2分)如图①,当点落在边上时,线段的长度为________;
(2)(2分)如图②,连接,当点落在线段上时,与相交于点,连接,求线段的长度;
(3)(3分)如图③,设点为边的中点,连接、、,在矩形旋转的过程中,求面积的最大值.
22.(7分)如图,在中,,将绕点逆时针旋转得到,点的对应点恰好落在斜边上,连接,已知.
(1)(3分)直接写出的长;
(2)(4分)求的长.
23.(8分)如图1,已知二次函数,与x轴相交于点,点为对称轴上的点,将线段绕点P逆时针旋转,得到线段,且点B在抛物线上.
(1)(4分)求抛物线的解析式;
(2)(4分)如图2,将该二次函数在x轴上方的图象沿x轴翻折到下方,图象的其余部分不变,得到一个新函数图象,当直线与新图象有3个交点时,求m的值.
24.(8分)如图,在直角坐标系中,点的坐标为,连结,将线段绕原点顺时针旋转,得到线段.
(1)(2分)求点的坐标;
(2)(2分)求经过三点的抛物线的解析式;
(3)(2分)在(2)中抛物线的对称轴上是否存在点,使周长最小 若存在,求点出的坐标和的周长;若不存在,请说明理由;
(4)(2分)如果点是(2)中的抛物线上的动点,那么是否存在点使得的面积为:;若有,求出此时点的横坐标;若没有,请说明理由.
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】A
4.【答案】D
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】5
12.【答案】9
13.【答案】
14.【答案】3
15.【答案】(2,10)或(﹣2,0)
16.【答案】65°
17.【答案】
18.【答案】(1)A;130
(2),
19.【答案】
20.【答案】解:∵正方形,
∴,
∵绕着点B旋转后能到达的位置,
∴,
∴.
21.【答案】(1)
(2)
(3)
22.【答案】(1)解:将绕点逆时针旋转得到,∴,
∴,,
∴的长为
(2)解:在中,,,由勾股定理得:,
由(1)可知,,
∴,,,
∴,
在中,根据勾股定理得:,
∴的长为
23.【答案】(1)
(2)或
24.【答案】(1);
(2);
(3),
(4)的横坐标为或.
同课章节目录
