用空间向量研究距离、夹角问题第一课时-高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 用空间向量研究距离、夹角问题第一课时-高二上学期数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 922.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 22:29:12 | ||
图片预览





文档简介
(共21张PPT)
第一章 空间向量与立体几何
1.4 空间向量的应用
1.4.2 用空间向量研究距离、 夹角问题
(第一课时)
一
二
三
学习目标
理解点到直线、点到平面的距离公式及其推导
了解利用空间向量求点到直线、点到平面、两平行直线、直线到平面、两平行平面的距离的思想
能利用距离公式解决相关的距离问题,归纳总结解决立体几何问题的“三部曲”
学习目标
复习回顾
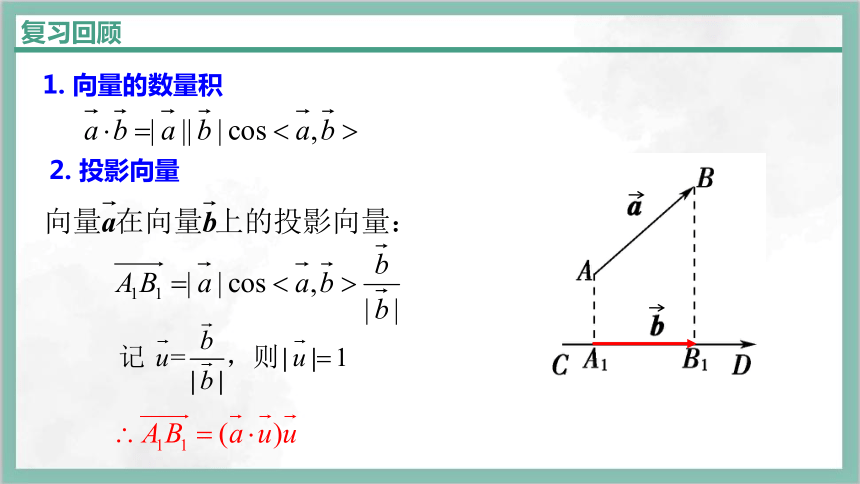
1. 向量的数量积
2. 投影向量
新课导入
问题1 空间中有哪些距离问题?
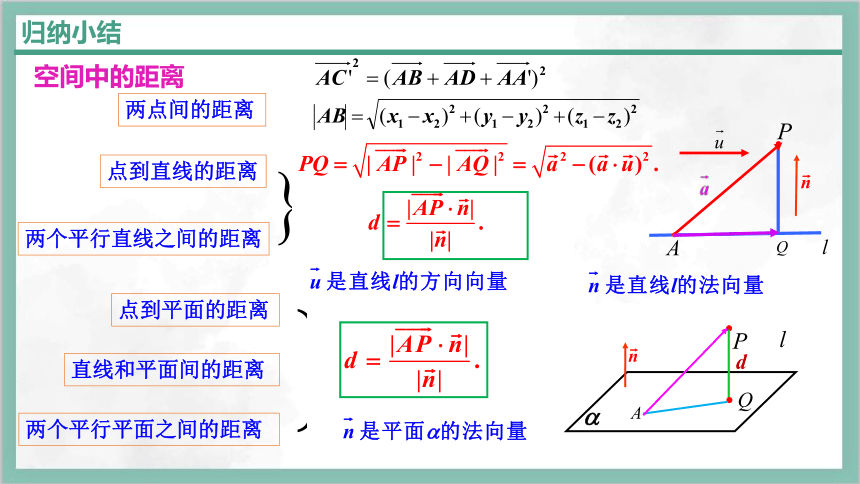
空间中的距离
两点间的距离、点到直线的距离、两平行线间的距离
点到平面的距离、线到平面的距离、两平行平面间的距离
我们该如何用空间向量解决这些距离?
接下来我们一起探究这些距离公式及推导!
空间向量的模
新知探究
问题1 已知直线l 的单位方向向量为 ,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离
如图,向量 在直线l上的投影向量为 ,则△APQ是直角三角形,因为A,P都是定点,所以 与 的夹角∠PAQ都是确定的. 于是可求 再利用勾股定理,可求出点P到直线l的距离PQ.
设 ,则向量 在直线l上的投影向量
在Rt△APQ中,由勾股定理,得
若直线l的法向量为 ,则点P到直线l的距离为
新知探究
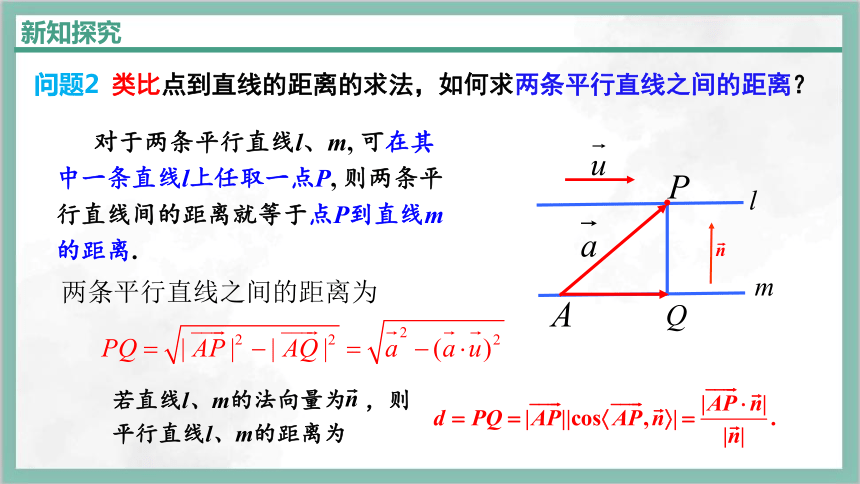
问题2 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
对于两条平行直线l、m, 可在其中一条直线l上任取一点P, 则两条平行直线间的距离就等于点P到直线m的距离.
若直线l、m的法向量为 ,则平行直线l、m的距离为
新知探究
问题3 如图,已知平面α外一点P,如何用空间向量求点P到平面α的距离d?
α
P
已知平面α的一个法向量为
A
点 A是平面α内的一个定点,点P是平面α外一点
Q
过点P作平面α的垂线l,交平面α于点Q,
连结QA、PA
平面外一点到平面的距离等于连接此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.
新知探究
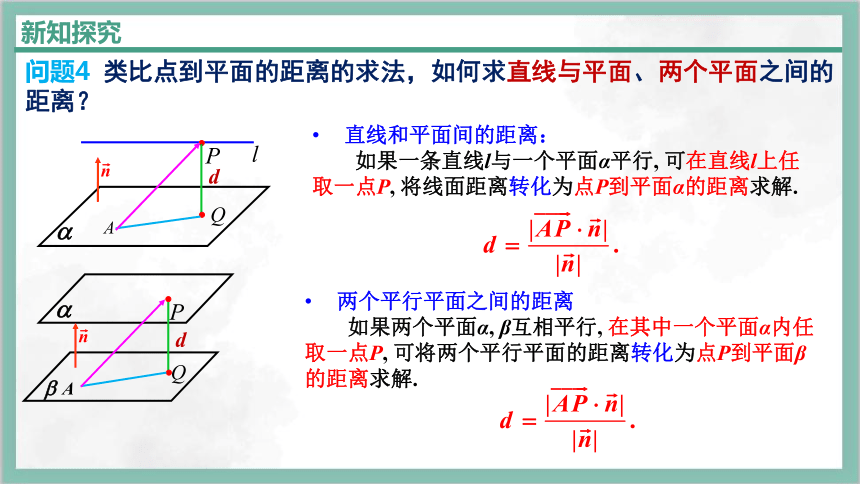
问题4 类比点到平面的距离的求法,如何求直线与平面、两个平面之间的距离?
l
直线和平面间的距离:
如果一条直线l与一个平面α平行, 可在直线l上任取一点P, 将线面距离转化为点P到平面α的距离求解.
两个平行平面之间的距离
如果两个平面α, β互相平行, 在其中一个平面α内任取一点P, 可将两个平行平面的距离转化为点P到平面β的距离求解.
d
d
A
A
归纳小结
直线和平面间的距离
两个平行平面之间的距离
点到平面的距离
两个平行直线之间的距离
点到直线的距离
l
d
A
空间中的距离
两点间的距离
P34-例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点.
(1) 求点B到直线AC1的距离; (2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
典例解析
解:
P34-例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点. (2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
典例解析
解:
解题提升
用向量法求平面α一个点P 到平面α的距离的步骤:
(3) 利用点到平面的距离公式即可求出点到平面的距离d.
(1) 求出该平面α的一个法向量 ;
α
A
Q
P
d
(2) 找出从点P出发的平面的任一条斜线段对应的向量 ;
解题提升
用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何结论.
(化为向量问题)
(进行向量运算)
(回到图形)
巩固练习
课本P35
1. 在棱长为1的正方体ABCD-A1B1C1D1中,
点A到平面B1C的距离等于_____;
直线DC到平面AB1的距离等于_______ ;
平面DA1到平面CB1的距离等于_______.
1
1
1
B
A
A1
B1
C1
D1
C
D
x
y
z
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
(2) 求直线FC1到直线AE的距离;
(3) 求点A1到平面AB1E的距离;
(4) 求直线FC1到平面AB1E的距离.
B
A
A1
B1
C1
D1
C
D
E
F
x
y
z
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
B
A
A1
B1
C1
D1
C
D
E
F
M
巩固练习
课本P35
几何法
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点. (2) 求直线FC1到直线AE的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.(3) 求点A1到平面AB1E的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点. (4) 求直线FC1到平面AB1E的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
巩固练习
课本P35
3. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,求平面A1DB与平面D1CB1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
课堂小结
本节课你学会了哪些主要内容?
1. 点到直线的距离
2. 点到平面的距离
l
d
A
第一章 空间向量与立体几何
1.4 空间向量的应用
1.4.2 用空间向量研究距离、 夹角问题
(第一课时)
一
二
三
学习目标
理解点到直线、点到平面的距离公式及其推导
了解利用空间向量求点到直线、点到平面、两平行直线、直线到平面、两平行平面的距离的思想
能利用距离公式解决相关的距离问题,归纳总结解决立体几何问题的“三部曲”
学习目标
复习回顾
1. 向量的数量积
2. 投影向量
新课导入
问题1 空间中有哪些距离问题?
空间中的距离
两点间的距离、点到直线的距离、两平行线间的距离
点到平面的距离、线到平面的距离、两平行平面间的距离
我们该如何用空间向量解决这些距离?
接下来我们一起探究这些距离公式及推导!
空间向量的模
新知探究
问题1 已知直线l 的单位方向向量为 ,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离
如图,向量 在直线l上的投影向量为 ,则△APQ是直角三角形,因为A,P都是定点,所以 与 的夹角∠PAQ都是确定的. 于是可求 再利用勾股定理,可求出点P到直线l的距离PQ.
设 ,则向量 在直线l上的投影向量
在Rt△APQ中,由勾股定理,得
若直线l的法向量为 ,则点P到直线l的距离为
新知探究
问题2 类比点到直线的距离的求法,如何求两条平行直线之间的距离?
对于两条平行直线l、m, 可在其中一条直线l上任取一点P, 则两条平行直线间的距离就等于点P到直线m的距离.
若直线l、m的法向量为 ,则平行直线l、m的距离为
新知探究
问题3 如图,已知平面α外一点P,如何用空间向量求点P到平面α的距离d?
α
P
已知平面α的一个法向量为
A
点 A是平面α内的一个定点,点P是平面α外一点
Q
过点P作平面α的垂线l,交平面α于点Q,
连结QA、PA
平面外一点到平面的距离等于连接此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.
新知探究
问题4 类比点到平面的距离的求法,如何求直线与平面、两个平面之间的距离?
l
直线和平面间的距离:
如果一条直线l与一个平面α平行, 可在直线l上任取一点P, 将线面距离转化为点P到平面α的距离求解.
两个平行平面之间的距离
如果两个平面α, β互相平行, 在其中一个平面α内任取一点P, 可将两个平行平面的距离转化为点P到平面β的距离求解.
d
d
A
A
归纳小结
直线和平面间的距离
两个平行平面之间的距离
点到平面的距离
两个平行直线之间的距离
点到直线的距离
l
d
A
空间中的距离
两点间的距离
P34-例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点.
(1) 求点B到直线AC1的距离; (2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
典例解析
解:
P34-例6 如图示,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段AB的中点,F为线段AB的中点. (2) 求直线FC到平面AEC1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
典例解析
解:
解题提升
用向量法求平面α一个点P 到平面α的距离的步骤:
(3) 利用点到平面的距离公式即可求出点到平面的距离d.
(1) 求出该平面α的一个法向量 ;
α
A
Q
P
d
(2) 找出从点P出发的平面的任一条斜线段对应的向量 ;
解题提升
用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何结论.
(化为向量问题)
(进行向量运算)
(回到图形)
巩固练习
课本P35
1. 在棱长为1的正方体ABCD-A1B1C1D1中,
点A到平面B1C的距离等于_____;
直线DC到平面AB1的距离等于_______ ;
平面DA1到平面CB1的距离等于_______.
1
1
1
B
A
A1
B1
C1
D1
C
D
x
y
z
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
(2) 求直线FC1到直线AE的距离;
(3) 求点A1到平面AB1E的距离;
(4) 求直线FC1到平面AB1E的距离.
B
A
A1
B1
C1
D1
C
D
E
F
x
y
z
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.
(1) 求点A1到直线B1E的距离;
B
A
A1
B1
C1
D1
C
D
E
F
M
巩固练习
课本P35
几何法
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点. (2) 求直线FC1到直线AE的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点.(3) 求点A1到平面AB1E的距离;
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
巩固练习
课本P35
2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为线段DD1的中点,F为线段BB1的中点. (4) 求直线FC1到平面AB1E的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
E
F
巩固练习
课本P35
3. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,求平面A1DB与平面D1CB1的距离.
x
y
z
B
A
A1
B1
C1
D1
C
D
课堂小结
本节课你学会了哪些主要内容?
1. 点到直线的距离
2. 点到平面的距离
l
d
A
