人教A版高中数学选择性必修第一册1.2空间向量基本定理
文档属性
| 名称 | 人教A版高中数学选择性必修第一册1.2空间向量基本定理 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 22:31:01 | ||
图片预览








文档简介
(共23张PPT)
1.2空间向量基本定理
共线向量定理:
共面向量定理:
复习引入
平面向量基本定理:
平面向量的正交分解及坐标表示
x
y
o
复习引入
下面我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论。
情境导学
情境导学
学习新知
P
O
图1.2-1
Q
问题探究
类似平面向量基本定理,我们有空间向量基本定理.
都叫做基向量
注:
如果三个向量 不共面,那么对空间任一向量 ,存在有序实数组{x,y,z}使
(1)空间任意三个不共面的向量都可构成空间的一个基底.基底选定后,空间的所有向量均可由基底唯一表示;不同基底下,同一向量的表达式也有可能不同.
特别提示:对于基底{ },除了应知道
不共面,还应明确:
(3)由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 .
(2)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念.
学习新知
(4)若{a,b,c}是空间的一个基底,且存在实数x,y,z使得xa+yb+zc=0,则有x=y=z=0.( )
√
做一做
×
√
√
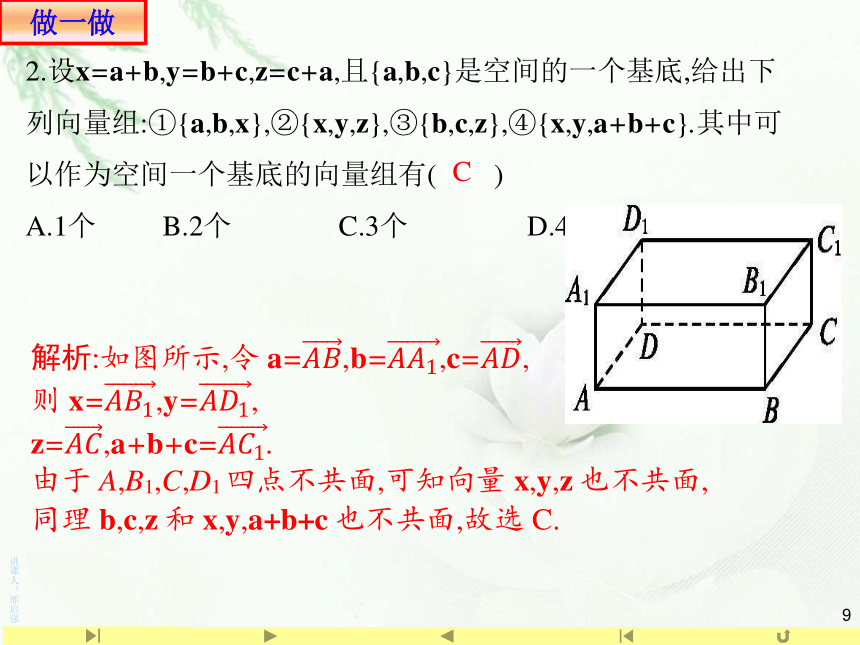
2.设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底,给出下列向量组:①{a,b,x},②{x,y,z},③{b,c,z},④{x,y,a+b+c}.其中可以作为空间一个基底的向量组有( )
A.1个 B.2个 C.3个 D.4个
C
做一做
做一做
空间向量的正交分解
x
y
z
学习新知
Q
P
O
典型讲评
例1如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且
用向量 表示 .
例2如图,在平行六面体ABCD-A1B1C1D1中,AB=4, AD=4,AA1=5,
∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M, N分别为D1C1,C1B1的中点,求证MN⊥AC1.
典型讲评
典型讲评
例3如图,正方体ABCD-A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;(2)求CE与AG所成角的余弦值.
所以EF//AC.
1.在正方体ABCD-A1B1C1D1中,可以作为空间向量的一组基底的是( )
C
解析:只有选项C中的三个向量是不共面的,可以作为一个基底.
A
达标练习
3.下列说法正确的是( )
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
C
解析:A项中应是不共面的三个向量构成空间向量的基底;
B项,空间基底有无数个;
D项中因为基底不唯一,所以D错.故选C.
达标练习
4.已知空间四边形
求证: 。
证明:∵
达标练习
达标练习
6、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.
达标练习
应用空间向量基本定理可以证明空间的线线垂直、线线平行,可求两条异面直线所成的角等.
第一根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0;
(2)若证明线线平行,只需证明两向量共线;
(3)若要求异面直线所成的角,则转化为两向量的夹角(或其补角).
课堂小结
5.若{a,b,c}是空间的一个基底,试判断{a+b,b+c,c+a}能否作为空间的一个基底.
解:假设a+b,b+c,c+a共面,则存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),即a+b=μa+λb+(λ+μ)c.
∵{a,b,c}是空间的一个基底,∴a,b,c不共面.
即不存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),
∴a+b,b+c,c+a不共面.
故{a+b,b+c,c+a}能作为空间的一个基底.
1.2空间向量基本定理
共线向量定理:
共面向量定理:
复习引入
平面向量基本定理:
平面向量的正交分解及坐标表示
x
y
o
复习引入
下面我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论。
情境导学
情境导学
学习新知
P
O
图1.2-1
Q
问题探究
类似平面向量基本定理,我们有空间向量基本定理.
都叫做基向量
注:
如果三个向量 不共面,那么对空间任一向量 ,存在有序实数组{x,y,z}使
(1)空间任意三个不共面的向量都可构成空间的一个基底.基底选定后,空间的所有向量均可由基底唯一表示;不同基底下,同一向量的表达式也有可能不同.
特别提示:对于基底{ },除了应知道
不共面,还应明确:
(3)由于可视 为与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含着它们都不是 .
(2)一个基底是指一个向量组,一个基向量是指基底中的某一个向量,二者是相关连的不同概念.
学习新知
(4)若{a,b,c}是空间的一个基底,且存在实数x,y,z使得xa+yb+zc=0,则有x=y=z=0.( )
√
做一做
×
√
√
2.设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底,给出下列向量组:①{a,b,x},②{x,y,z},③{b,c,z},④{x,y,a+b+c}.其中可以作为空间一个基底的向量组有( )
A.1个 B.2个 C.3个 D.4个
C
做一做
做一做
空间向量的正交分解
x
y
z
学习新知
Q
P
O
典型讲评
例1如图,M是四面体OABC的棱BC的中点,点N在线段OM上,点P在线段AN上,且
用向量 表示 .
例2如图,在平行六面体ABCD-A1B1C1D1中,AB=4, AD=4,AA1=5,
∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M, N分别为D1C1,C1B1的中点,求证MN⊥AC1.
典型讲评
典型讲评
例3如图,正方体ABCD-A'B'C'D'的棱长为1,E,F,G分别为C'D',A'D',D'D的中点.
(1)求证:EF//AC;(2)求CE与AG所成角的余弦值.
所以EF//AC.
1.在正方体ABCD-A1B1C1D1中,可以作为空间向量的一组基底的是( )
C
解析:只有选项C中的三个向量是不共面的,可以作为一个基底.
A
达标练习
3.下列说法正确的是( )
A.任何三个不共线的向量可构成空间向量的一个基底
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
C
解析:A项中应是不共面的三个向量构成空间向量的基底;
B项,空间基底有无数个;
D项中因为基底不唯一,所以D错.故选C.
达标练习
4.已知空间四边形
求证: 。
证明:∵
达标练习
达标练习
6、已知向量{a,b,c}是空间的一个基底.
求证:向量a+b,a-b,c能构成空间的一个基底.
达标练习
应用空间向量基本定理可以证明空间的线线垂直、线线平行,可求两条异面直线所成的角等.
第一根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0;
(2)若证明线线平行,只需证明两向量共线;
(3)若要求异面直线所成的角,则转化为两向量的夹角(或其补角).
课堂小结
5.若{a,b,c}是空间的一个基底,试判断{a+b,b+c,c+a}能否作为空间的一个基底.
解:假设a+b,b+c,c+a共面,则存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),即a+b=μa+λb+(λ+μ)c.
∵{a,b,c}是空间的一个基底,∴a,b,c不共面.
即不存在实数λ,μ,使得a+b=λ(b+c)+μ(c+a),
∴a+b,b+c,c+a不共面.
故{a+b,b+c,c+a}能作为空间的一个基底.
