第八单元数学广角-搭配(一)(含解析)-2024-2025学年二年级上册数学人教版
文档属性
| 名称 | 第八单元数学广角-搭配(一)(含解析)-2024-2025学年二年级上册数学人教版 |

|
|
| 格式 | doc | ||
| 文件大小 | 473.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-09 21:02:42 | ||
图片预览


文档简介
/ 让教学更有效 精品试卷 | 数学学科
第八单元数学广角-搭配(一)-2024-2025学年二年级上册数学人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.图中共有( )条不同的线段.
A.4 B.16 C.8 D.10
2.用2、3、0这三个数字能摆出( )个不同的两位数.
A.2 B.4 C.6
3.小红有3件上衣和2条裤子,每次穿1件上衣和1条裤子,可能有( )种穿法。
A.5 B.6 C.7
4.贝贝和亮亮去王老师家做客,王老师拿出三袋不同的糖分给贝贝和亮亮,每人各分一袋,一共有( )种不同的分法。21世纪教育网版权所有
A.6 B.5 C.3
5.4只小鸟进行羽毛球比赛,每两只小鸟都要赛一场,一共要赛几场?( )
A.4 B.12 C.6
6.3个人拥抱,每两个人都要拥抱一次,一共要拥抱( )次。
A.3次 B.4次 C.5次
二、填空题
7.有2元、5元、10元的人民币各一张,至少拿出2张,共能组成( )种不同的币值。
8.用0、3、6这三个数中的任意两个数求和,得数有( )种可能,其中最大的和与最小的和相差( )。【来源:21cnj*y.co*m】
9.三人下棋,每两人下一局,一共要下( )局.
10.从下面5名同学中选2名参加乒乓球男女混合双打比赛,一共有( )不同的选法。
11.赵叔叔,李叔叔,王叔叔排成一排拍照,一共有( ) 种不同的排法。
12.从《童话故事》、《神话故事》、《寓言故事》和《成语故事》四本书中任选两本,一共有( )种不同的选择方案。
13.从语文、数学、英语3本书中选2本,分给丽丽、聪聪各1本,一共有( )种不同的分法。
14.学校餐厅中午为学生提供2种不同的荤菜,2种不同的素菜,小明打算买一荤一素两种菜,一共有( )种不同的买法。
15.用3、6、9组成两位数,每个两位数的十位数和个位数不能一样,能组成( )个两位数,其中最大的是( ),最小的是( )。
16.用2、0和5组成两位数,每个两位数的十位数和个位数不能一样,能组成( )个两位数,其中最大的两位数是( ),最小的两位数是( ),它们相差( )。
17.从5、6、9三个数中每次取2个数求积,共有( )个不同的积。
三、判断题
18.用2、3、4三个数字可以组成6个两位数. ( )
19.四个班进行拔河比赛,每两个班要比一场,一共要比6场。( )
20.从上海到成都的快车,中途要停靠9个站,有55种不同的车票。( )
21.有4名同学去打羽毛球,每两人打一场,一共要打8场。( )
22.小红、小明、小青每两人握一次手,3人一共握6次手。 ( )
23.3个小朋友,每两个人打一次电话,一共要打6次电话。( )
四、计算题
24.口算.
4×4= 7×7= 32-15= 46+27-39=
5×7= 26-12= 8×7= 8×4-16=
30+65= 6+27= 45-9= 4×7+21=
2×5= 35+40= 9×6= 82-(3+25)=
72-3= 5×3= 42+23= 3×6+15=
五、作图题
25.按规律画图.
六、解答题
26.爸爸、妈妈和我一家三口坐成一排拍合影,一共有多少种不同的坐法?
27.从1~9这九个数字中,每次取2个数字,这两个数字的和都必须大于10,能有多少种取法?
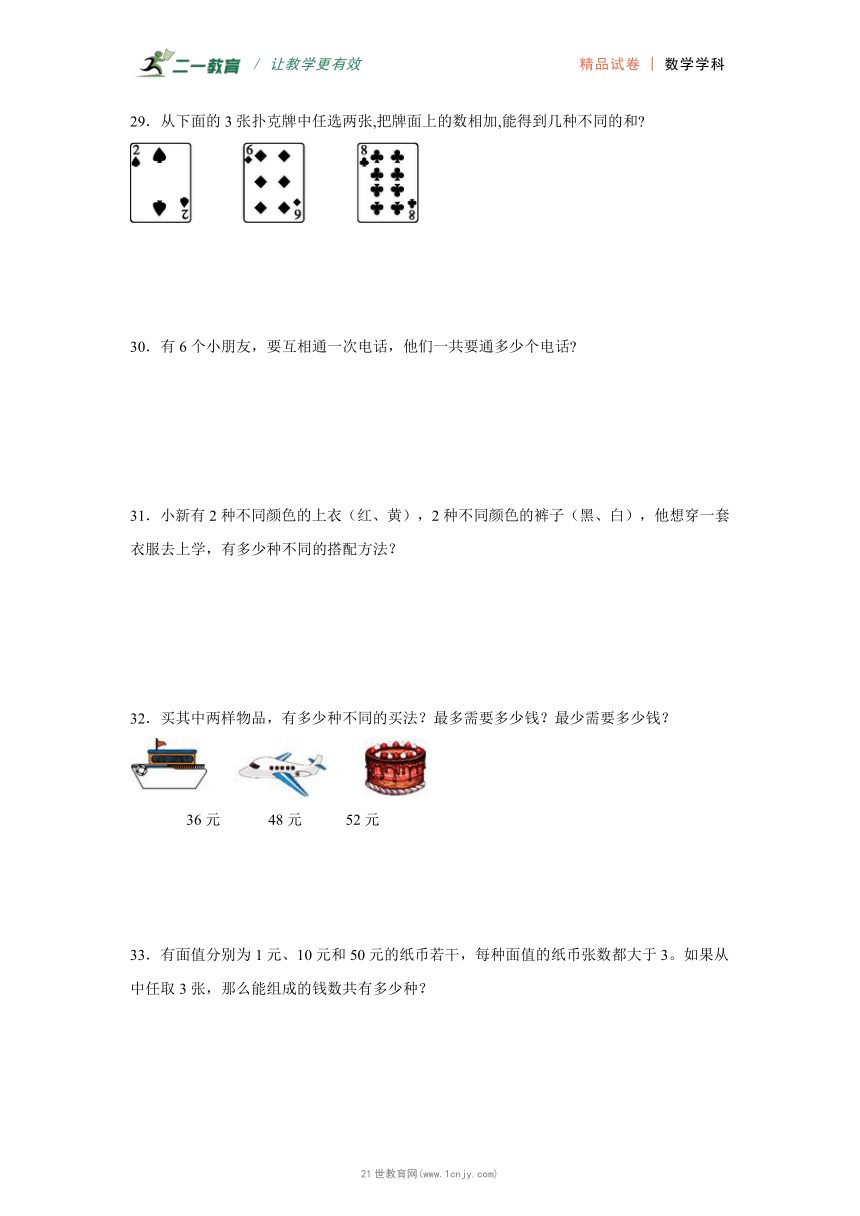
28.如图,小石头去动物园游玩。数一数从大门到猴山有( )条路可走。
请你设计一条能参观全部景点的线路。(每个景点只能去一次)
29.从下面的3张扑克牌中任选两张,把牌面上的数相加,能得到几种不同的和
30.有6个小朋友,要互相通一次电话,他们一共要通多少个电话
31.小新有2种不同颜色的上衣(红、黄),2种不同颜色的裤子(黑、白),他想穿一套衣服去上学,有多少种不同的搭配方法?21·世纪*教育网
32.买其中两样物品,有多少种不同的买法?最多需要多少钱?最少需要多少钱?
36元 48元 52元
33.有面值分别为1元、10元和50元的纸币若干,每种面值的纸币张数都大于3。如果从中任取3张,那么能组成的钱数共有多少种?【来源:21·世纪·教育·网】
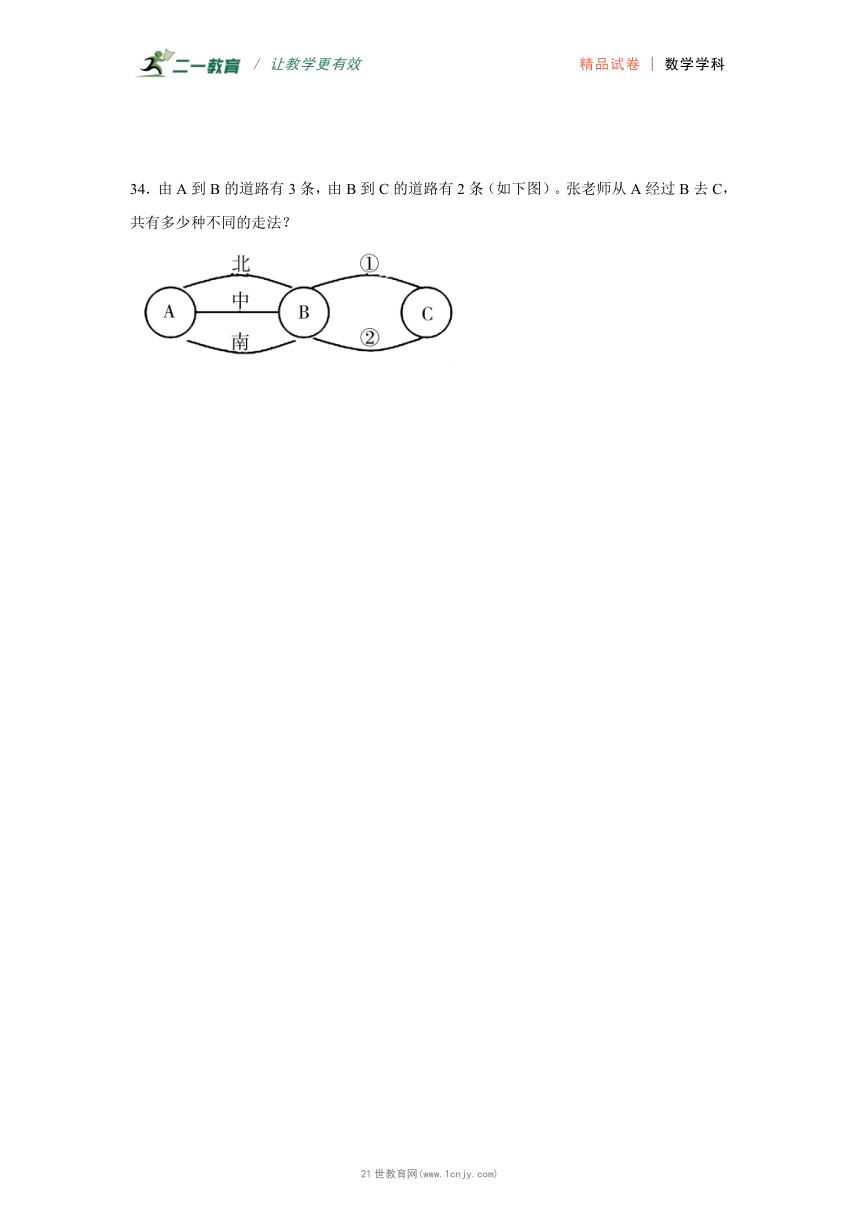
34.由A到B的道路有3条,由B到C的道路有2条(如下图)。张老师从A经过B去C,共有多少种不同的走法?21cnjy.com
参考答案:
1.D
【分析】先一段一段地找出基本线段的条数,再数出组合线段的条数,然后再相加即可.
【详解】解:4+3+2+1=10(条)
故答案为10.
2.B
3.B
4.A
【分析】先确定一种糖给哪位小朋友,另一位小朋友就有2种分法,3种糖就有3个2种分法,即6种不同的分法。2-1-c-n-j-y
【详解】3×2=6(种)
根据分析得出有6种不同的分法。
故答案为:A
5.C
【分析】根据题意,每只小鸟都要和另外3只小鸟比赛一场,据此连线解答。
【详解】如图:
3+2+1=6(场)
一共要赛6场。
故答案为:C
【点睛】本题考查搭配问题,连线时注意不要重复,也可以给4只小鸟编号,两两组合得出结论。
6.A
【分析】根据题意,三个人每两个人都要拥抱一次,假设是ABC三个人,A需要与另外两个人拥抱,共拥抱两次,B与C拥抱一次,C已经与其他两个人拥抱过,由此可知共需要拥抱3次,据此解答。【版权所有:21教育】
【详解】由分析可知:
2+1=3(次)
故答案为:A
【点睛】本题主要考查搭配知识,解答本题可以用画图连线的方法解答。
7.4
【分析】用列举法一一列举出所有情况即可得出答案。
【详解】取2张的情况:
1张2元和1张5元,合起来的币值是2+5=7(元)
1张2元和1张10元,合起来的币值是2+10=12(元)
1张5元和1张10元,合起来的币值是5+10=15(元)
取3张的情况:
1张2元,1张5元,1张10元,合起来的币值是
2+5+10
=7+10
=17(元)
所以,一共能组成4种不同的币值。
8. 3 6
【分析】先把0、3、6这三个数两两相加,求出和,然后数一数,即可知道得数有几种可能;
接着比较大小,最后用最大的和减去最小的和,求出差,即可解决。
【详解】0+3=3
0+6=6
3+6=9
3<6<9
9-3=6
故,用0、3、6这三个数中的任意两个数求和,得数有3种可能,其中最大的和与最小的和相差6。
9.3
【解析】略
10.6
【分析】题中有3个男孩,2个女孩。每一个男孩和一个女孩组合,有2种选法;共3个男孩,也就是有2×3种选法。【出处:21教育名师】
【详解】2×3=6(种)
一共有6种不同的选法。
11.6
【解析】略
12.6
【分析】由题意可知,从《童话故事》、《神话故事》、《寓言故事》和《成语故事》四本书中任选两本,可以这样选:《童话故事》+《神话故事》、《童话故事》+《寓言故事》、《童话故事》+《成语故事》、《神话故事》+《寓言故事》、《神话故事》+《成语故事》、《寓言故事》+《成语故事》,一共有6种不同的选择方案。21*cnjy*com
【详解】由分析可得:
从《童话故事》、《神话故事》、《寓言故事》和《成语故事》四本书中任选两本,一共有( 6 )种不同的选择方案。
【点睛】熟练掌握搭配是解决此题的关键。
13.6
【分析】从三本书中选1本,送给丽丽有3种选择,再从剩下的2本书中选1本,送给聪聪有2种选择,根据乘法原理可得,共有3×2=6种选择。
【详解】3×2=6(种)
所以一共有6种。
14.4
【详解】略
15. 6 96 36
【分析】把3、6、9组成的两位数一一列举出来(每个两位数的十位数和个位数不能一样),数一数有几个两位数,然后比较大小,即可解决。21*cnjy*com
【详解】用3、6、9组成的两位数有(每个两位数的十位数和个位数不一样):36、63、39、93、69、96,一共有6个。
96>93>69>63>39>36;
即,用3、6、9组成两位数,每个两位数的十位数和个位数不能一样,能组成6个两位数,其中最大的是96,最小的是36。
16. 4 52 20 32
【解析】略
17.3
【分析】因为从三个数中,每次取出两个数相乘,每个数都可以组成两个乘法算式,然后把相同的去掉即可。
【详解】从5、6、 9三个数中每次取2个数求积,共有3个不同的积。
5×6=30
5×9=45
6×9=54
18.√
【详解】略
19.√
【分析】由于每个班都要与另外的3个班各比赛一场,也就是每个班都要比赛3场,那么一共要比赛:3×4=12(场);21教育网
又因为两个班之间只比赛一场,去掉重复计算的情况,实际比赛:12÷2=6(场);据此解决。
【详解】(3-1)×4÷2
=3×4÷2
=12÷2
=6(场)
即,四个班进行拔河比赛,每两个班要比一场,一共要比6场。此说法正确。
故答案为:√
20.√
【分析】根据数线段的方法在实际生活中的应用,只要掌握数线段的方法即可算出。中途要停靠9个站,连同上海和成都在内,一共有11个站,相当于11个点,有10条线段,那么就有(10+9+8+7+6+5+4+3+2+1)种不同的车票。www.21-cn-jy.com
【详解】10+9+8+7+6+5+4+3+2+1=55(种),则有55种不同的车票。原题说法正确。
故答案为:√
21.×
【分析】每人都要和另外3人打一场,用4×3,再将积除以2除去重复的部分,求出一共需要打多少场。
【详解】4×3÷2
=12÷2
=6(场)
所以,一共要打6场。
故答案为:×
【点睛】本题考查了搭配问题,牢记要去除重复部分是解题的关键。
22.×
【详解】略
23.×
【详解】略
24.4×4=16 7×7=49 32-15=17 46+27-39=34
5×7=35 26-12=14 8×7=56 8×4-16=16
30+65=95 6+27=33 45-9=36 4×7+21=49
2×5=10 35+40=75 9×6=54 82-(3+25)=54
72-3=69 5×3=15 42+23=65 3×6+15=33
【详解】略
25.;;
【分析】观察图形的规律.
【详解】圆圈的数量从2到4,再到6,依次加2个圈(1列),因此图形如下:
;;
26.6种
【分析】具体坐法如下表所示:
坐法 左 中 右
第1种 我 爸爸 妈妈
第2种 我 妈妈 爸爸
第3种 爸爸 我 妈妈
第4种 爸爸 妈妈 我
第5种 妈妈 我 爸爸
第6种 妈妈 爸爸 我
【详解】2×3=6(种)
答:一共有6种不同的坐法。
【点睛】熟练掌握搭配问题的计算方法是解答此题的关键。
27.16种
【详解】 第1个取2,第2个取9,有1种不同取法;
第1个取3,第2个可取8、9,有2种不同取法;
第1个取4,第2个可取7、8、9,有3种不同取法;
第1个取5,第2个可取6、7、8、9,有4种不同取法;
第1个取6,第2个可取7、8、9,有3种不同取法;
第1个取7,第2个可取8、9,有2种不同取法;
第1个取8,第2个可取9,有1种不同取法。
那么能有4×4=16种不同取法。
28.9;
大门→熊猫馆→狮虎馆→猴山→鸟语林→海豚馆→大象馆→大门。(答案不唯一)
【分析】从大门经过熊猫馆然后经过狮虎馆(海豚馆、鸟语林)有3条路可走,再从大门经过大象馆、鸟语林又各有3条,则总的线路有3个3条,用乘法计算。只要设计的路线不重复,且能参观全部景点即可。21·cn·jy·com
【详解】3×3=9(条)
从大门到猴山有9条路可走。
设计线路如下:大门→熊猫馆→狮虎馆→猴山→鸟语林→海豚馆→大象馆→大门。(答案不唯一)
29.2+6=8 2+8=10 6+8=14 3种
【详解】略
30.15个
【分析】第一个小朋友需要和后面5个小朋友通话,共5次;第二个小朋友和后面4个小朋友各通话一次,共4次;第三个小朋友和后面3各小朋友各通一次,共3次;第四个小朋友和后面两个小朋友各通话一次,共2次;第五个和第六个小朋友通话一次即可。用加法计算通话的总次数。2·1·c·n·j·y
【详解】5+4+3+2+1=15(个)
答:他们一共要通15个电话。
31.4种
【分析】从2件上衣中选一件有2种选法;从两条裤子中选一件有2种选法;要配成一套衣服,红黑、红白、黄黑、黄白4种不同的搭配方法。即可得解。www-2-1-cnjy-com
【详解】可以有:红黑、红白、黄黑、黄白,共4种不同的搭配方法。
答:有4种不同的搭配方法。
【点睛】注意按顺序列出,不要遗漏。
32.三种, 100元,84元
【详解】48+52=100(元)
48+36=84(元)
52+36=88(元)
100>88>84
口答:有三种不同的买法,最多需要100元,最少需要84元。
33.10种
【分析】按取出的钱所含的面值种数分类,可能是1种面值,也可能是2种面值,也可能是3种面值,据此解答。21教育名师原创作品
【详解】(1)取出的3张可能是3张1元,或3张10元,或3张50元,共有3种可能;
(2)可能是2张1元1张10元,2张1元1张50元,2张10元1张1元,2张10元1张50元,2张50元1张1元,2张50元1张10元,共有6种可能;
(3)可能是1元、10元、50元各1张,有1种可能。
3+6+1=10(种)
答:能组成的钱数共有10种。
【点睛】本题考查搭配问题,要根据取出的钱所含的面值种数有规律地分类,避免多数或漏数。
34.6种
【分析】假如从A走北这条路走到B,再去C,可以走①或者②,有2种不同的走法;因为从A到B的道路有3条,那么共有2×3=6(种)不同的走法,如下图所示:
ABC ABC
ABC ABC
ABC ABC
【详解】2×3=6(种)
答:共有6种不同的走法。
【点睛】熟练掌握搭配问题的计算方法是解答此题的关键。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
第八单元数学广角-搭配(一)-2024-2025学年二年级上册数学人教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.图中共有( )条不同的线段.
A.4 B.16 C.8 D.10
2.用2、3、0这三个数字能摆出( )个不同的两位数.
A.2 B.4 C.6
3.小红有3件上衣和2条裤子,每次穿1件上衣和1条裤子,可能有( )种穿法。
A.5 B.6 C.7
4.贝贝和亮亮去王老师家做客,王老师拿出三袋不同的糖分给贝贝和亮亮,每人各分一袋,一共有( )种不同的分法。21世纪教育网版权所有
A.6 B.5 C.3
5.4只小鸟进行羽毛球比赛,每两只小鸟都要赛一场,一共要赛几场?( )
A.4 B.12 C.6
6.3个人拥抱,每两个人都要拥抱一次,一共要拥抱( )次。
A.3次 B.4次 C.5次
二、填空题
7.有2元、5元、10元的人民币各一张,至少拿出2张,共能组成( )种不同的币值。
8.用0、3、6这三个数中的任意两个数求和,得数有( )种可能,其中最大的和与最小的和相差( )。【来源:21cnj*y.co*m】
9.三人下棋,每两人下一局,一共要下( )局.
10.从下面5名同学中选2名参加乒乓球男女混合双打比赛,一共有( )不同的选法。
11.赵叔叔,李叔叔,王叔叔排成一排拍照,一共有( ) 种不同的排法。
12.从《童话故事》、《神话故事》、《寓言故事》和《成语故事》四本书中任选两本,一共有( )种不同的选择方案。
13.从语文、数学、英语3本书中选2本,分给丽丽、聪聪各1本,一共有( )种不同的分法。
14.学校餐厅中午为学生提供2种不同的荤菜,2种不同的素菜,小明打算买一荤一素两种菜,一共有( )种不同的买法。
15.用3、6、9组成两位数,每个两位数的十位数和个位数不能一样,能组成( )个两位数,其中最大的是( ),最小的是( )。
16.用2、0和5组成两位数,每个两位数的十位数和个位数不能一样,能组成( )个两位数,其中最大的两位数是( ),最小的两位数是( ),它们相差( )。
17.从5、6、9三个数中每次取2个数求积,共有( )个不同的积。
三、判断题
18.用2、3、4三个数字可以组成6个两位数. ( )
19.四个班进行拔河比赛,每两个班要比一场,一共要比6场。( )
20.从上海到成都的快车,中途要停靠9个站,有55种不同的车票。( )
21.有4名同学去打羽毛球,每两人打一场,一共要打8场。( )
22.小红、小明、小青每两人握一次手,3人一共握6次手。 ( )
23.3个小朋友,每两个人打一次电话,一共要打6次电话。( )
四、计算题
24.口算.
4×4= 7×7= 32-15= 46+27-39=
5×7= 26-12= 8×7= 8×4-16=
30+65= 6+27= 45-9= 4×7+21=
2×5= 35+40= 9×6= 82-(3+25)=
72-3= 5×3= 42+23= 3×6+15=
五、作图题
25.按规律画图.
六、解答题
26.爸爸、妈妈和我一家三口坐成一排拍合影,一共有多少种不同的坐法?
27.从1~9这九个数字中,每次取2个数字,这两个数字的和都必须大于10,能有多少种取法?
28.如图,小石头去动物园游玩。数一数从大门到猴山有( )条路可走。
请你设计一条能参观全部景点的线路。(每个景点只能去一次)
29.从下面的3张扑克牌中任选两张,把牌面上的数相加,能得到几种不同的和
30.有6个小朋友,要互相通一次电话,他们一共要通多少个电话
31.小新有2种不同颜色的上衣(红、黄),2种不同颜色的裤子(黑、白),他想穿一套衣服去上学,有多少种不同的搭配方法?21·世纪*教育网
32.买其中两样物品,有多少种不同的买法?最多需要多少钱?最少需要多少钱?
36元 48元 52元
33.有面值分别为1元、10元和50元的纸币若干,每种面值的纸币张数都大于3。如果从中任取3张,那么能组成的钱数共有多少种?【来源:21·世纪·教育·网】
34.由A到B的道路有3条,由B到C的道路有2条(如下图)。张老师从A经过B去C,共有多少种不同的走法?21cnjy.com
参考答案:
1.D
【分析】先一段一段地找出基本线段的条数,再数出组合线段的条数,然后再相加即可.
【详解】解:4+3+2+1=10(条)
故答案为10.
2.B
3.B
4.A
【分析】先确定一种糖给哪位小朋友,另一位小朋友就有2种分法,3种糖就有3个2种分法,即6种不同的分法。2-1-c-n-j-y
【详解】3×2=6(种)
根据分析得出有6种不同的分法。
故答案为:A
5.C
【分析】根据题意,每只小鸟都要和另外3只小鸟比赛一场,据此连线解答。
【详解】如图:
3+2+1=6(场)
一共要赛6场。
故答案为:C
【点睛】本题考查搭配问题,连线时注意不要重复,也可以给4只小鸟编号,两两组合得出结论。
6.A
【分析】根据题意,三个人每两个人都要拥抱一次,假设是ABC三个人,A需要与另外两个人拥抱,共拥抱两次,B与C拥抱一次,C已经与其他两个人拥抱过,由此可知共需要拥抱3次,据此解答。【版权所有:21教育】
【详解】由分析可知:
2+1=3(次)
故答案为:A
【点睛】本题主要考查搭配知识,解答本题可以用画图连线的方法解答。
7.4
【分析】用列举法一一列举出所有情况即可得出答案。
【详解】取2张的情况:
1张2元和1张5元,合起来的币值是2+5=7(元)
1张2元和1张10元,合起来的币值是2+10=12(元)
1张5元和1张10元,合起来的币值是5+10=15(元)
取3张的情况:
1张2元,1张5元,1张10元,合起来的币值是
2+5+10
=7+10
=17(元)
所以,一共能组成4种不同的币值。
8. 3 6
【分析】先把0、3、6这三个数两两相加,求出和,然后数一数,即可知道得数有几种可能;
接着比较大小,最后用最大的和减去最小的和,求出差,即可解决。
【详解】0+3=3
0+6=6
3+6=9
3<6<9
9-3=6
故,用0、3、6这三个数中的任意两个数求和,得数有3种可能,其中最大的和与最小的和相差6。
9.3
【解析】略
10.6
【分析】题中有3个男孩,2个女孩。每一个男孩和一个女孩组合,有2种选法;共3个男孩,也就是有2×3种选法。【出处:21教育名师】
【详解】2×3=6(种)
一共有6种不同的选法。
11.6
【解析】略
12.6
【分析】由题意可知,从《童话故事》、《神话故事》、《寓言故事》和《成语故事》四本书中任选两本,可以这样选:《童话故事》+《神话故事》、《童话故事》+《寓言故事》、《童话故事》+《成语故事》、《神话故事》+《寓言故事》、《神话故事》+《成语故事》、《寓言故事》+《成语故事》,一共有6种不同的选择方案。21*cnjy*com
【详解】由分析可得:
从《童话故事》、《神话故事》、《寓言故事》和《成语故事》四本书中任选两本,一共有( 6 )种不同的选择方案。
【点睛】熟练掌握搭配是解决此题的关键。
13.6
【分析】从三本书中选1本,送给丽丽有3种选择,再从剩下的2本书中选1本,送给聪聪有2种选择,根据乘法原理可得,共有3×2=6种选择。
【详解】3×2=6(种)
所以一共有6种。
14.4
【详解】略
15. 6 96 36
【分析】把3、6、9组成的两位数一一列举出来(每个两位数的十位数和个位数不能一样),数一数有几个两位数,然后比较大小,即可解决。21*cnjy*com
【详解】用3、6、9组成的两位数有(每个两位数的十位数和个位数不一样):36、63、39、93、69、96,一共有6个。
96>93>69>63>39>36;
即,用3、6、9组成两位数,每个两位数的十位数和个位数不能一样,能组成6个两位数,其中最大的是96,最小的是36。
16. 4 52 20 32
【解析】略
17.3
【分析】因为从三个数中,每次取出两个数相乘,每个数都可以组成两个乘法算式,然后把相同的去掉即可。
【详解】从5、6、 9三个数中每次取2个数求积,共有3个不同的积。
5×6=30
5×9=45
6×9=54
18.√
【详解】略
19.√
【分析】由于每个班都要与另外的3个班各比赛一场,也就是每个班都要比赛3场,那么一共要比赛:3×4=12(场);21教育网
又因为两个班之间只比赛一场,去掉重复计算的情况,实际比赛:12÷2=6(场);据此解决。
【详解】(3-1)×4÷2
=3×4÷2
=12÷2
=6(场)
即,四个班进行拔河比赛,每两个班要比一场,一共要比6场。此说法正确。
故答案为:√
20.√
【分析】根据数线段的方法在实际生活中的应用,只要掌握数线段的方法即可算出。中途要停靠9个站,连同上海和成都在内,一共有11个站,相当于11个点,有10条线段,那么就有(10+9+8+7+6+5+4+3+2+1)种不同的车票。www.21-cn-jy.com
【详解】10+9+8+7+6+5+4+3+2+1=55(种),则有55种不同的车票。原题说法正确。
故答案为:√
21.×
【分析】每人都要和另外3人打一场,用4×3,再将积除以2除去重复的部分,求出一共需要打多少场。
【详解】4×3÷2
=12÷2
=6(场)
所以,一共要打6场。
故答案为:×
【点睛】本题考查了搭配问题,牢记要去除重复部分是解题的关键。
22.×
【详解】略
23.×
【详解】略
24.4×4=16 7×7=49 32-15=17 46+27-39=34
5×7=35 26-12=14 8×7=56 8×4-16=16
30+65=95 6+27=33 45-9=36 4×7+21=49
2×5=10 35+40=75 9×6=54 82-(3+25)=54
72-3=69 5×3=15 42+23=65 3×6+15=33
【详解】略
25.;;
【分析】观察图形的规律.
【详解】圆圈的数量从2到4,再到6,依次加2个圈(1列),因此图形如下:
;;
26.6种
【分析】具体坐法如下表所示:
坐法 左 中 右
第1种 我 爸爸 妈妈
第2种 我 妈妈 爸爸
第3种 爸爸 我 妈妈
第4种 爸爸 妈妈 我
第5种 妈妈 我 爸爸
第6种 妈妈 爸爸 我
【详解】2×3=6(种)
答:一共有6种不同的坐法。
【点睛】熟练掌握搭配问题的计算方法是解答此题的关键。
27.16种
【详解】 第1个取2,第2个取9,有1种不同取法;
第1个取3,第2个可取8、9,有2种不同取法;
第1个取4,第2个可取7、8、9,有3种不同取法;
第1个取5,第2个可取6、7、8、9,有4种不同取法;
第1个取6,第2个可取7、8、9,有3种不同取法;
第1个取7,第2个可取8、9,有2种不同取法;
第1个取8,第2个可取9,有1种不同取法。
那么能有4×4=16种不同取法。
28.9;
大门→熊猫馆→狮虎馆→猴山→鸟语林→海豚馆→大象馆→大门。(答案不唯一)
【分析】从大门经过熊猫馆然后经过狮虎馆(海豚馆、鸟语林)有3条路可走,再从大门经过大象馆、鸟语林又各有3条,则总的线路有3个3条,用乘法计算。只要设计的路线不重复,且能参观全部景点即可。21·cn·jy·com
【详解】3×3=9(条)
从大门到猴山有9条路可走。
设计线路如下:大门→熊猫馆→狮虎馆→猴山→鸟语林→海豚馆→大象馆→大门。(答案不唯一)
29.2+6=8 2+8=10 6+8=14 3种
【详解】略
30.15个
【分析】第一个小朋友需要和后面5个小朋友通话,共5次;第二个小朋友和后面4个小朋友各通话一次,共4次;第三个小朋友和后面3各小朋友各通一次,共3次;第四个小朋友和后面两个小朋友各通话一次,共2次;第五个和第六个小朋友通话一次即可。用加法计算通话的总次数。2·1·c·n·j·y
【详解】5+4+3+2+1=15(个)
答:他们一共要通15个电话。
31.4种
【分析】从2件上衣中选一件有2种选法;从两条裤子中选一件有2种选法;要配成一套衣服,红黑、红白、黄黑、黄白4种不同的搭配方法。即可得解。www-2-1-cnjy-com
【详解】可以有:红黑、红白、黄黑、黄白,共4种不同的搭配方法。
答:有4种不同的搭配方法。
【点睛】注意按顺序列出,不要遗漏。
32.三种, 100元,84元
【详解】48+52=100(元)
48+36=84(元)
52+36=88(元)
100>88>84
口答:有三种不同的买法,最多需要100元,最少需要84元。
33.10种
【分析】按取出的钱所含的面值种数分类,可能是1种面值,也可能是2种面值,也可能是3种面值,据此解答。21教育名师原创作品
【详解】(1)取出的3张可能是3张1元,或3张10元,或3张50元,共有3种可能;
(2)可能是2张1元1张10元,2张1元1张50元,2张10元1张1元,2张10元1张50元,2张50元1张1元,2张50元1张10元,共有6种可能;
(3)可能是1元、10元、50元各1张,有1种可能。
3+6+1=10(种)
答:能组成的钱数共有10种。
【点睛】本题考查搭配问题,要根据取出的钱所含的面值种数有规律地分类,避免多数或漏数。
34.6种
【分析】假如从A走北这条路走到B,再去C,可以走①或者②,有2种不同的走法;因为从A到B的道路有3条,那么共有2×3=6(种)不同的走法,如下图所示:
ABC ABC
ABC ABC
ABC ABC
【详解】2×3=6(种)
答:共有6种不同的走法。
【点睛】熟练掌握搭配问题的计算方法是解答此题的关键。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世教育网(www.1cnjy.com)
