北师大八上6.4.2数据的离散程度(2)
文档属性
| 名称 | 北师大八上6.4.2数据的离散程度(2) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-10 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
第六章 数据的分析
6.4.2数据的离散程度(2)
北师大版 数学 八年级 上册
学习目标
1.进一步了解极差、方差、标准差的求法.
2.会用极差、方差、标准差对实际问题做出判断.
情景导入
答: 一组数据中的最大值减去最小值所得的差叫做这组数据的极差.
1.哪些统计量可表示一组数据的集中趋势
答:一组数据的集中趋势可由平均数,众数,中位数表示
2.何为一组数据的极差
情景导入
3.极差反映了这组数据哪方面的特征
答:极差反映的是这组数据的变化范围或变化幅度.
4.极差有什么局限性
答:极差受极端值的影响较大,不能准确反映数据
的波动情况.
探索新知
方差的应用
一
如图是某一天A、B两地的气温变化图,回答问题:
(1)这一天A、B两地的平均气温分别是多少?
解:(1)A地的平均气温是20.42℃,
B地的平均气温是21.35℃;
探索新知
(2)A地这一天气温的极差、方差分别是多少?B地呢?
(2)A地的极差是9.5℃,方差是7.76,
B地的极差是6℃,方差是2.78;
探索新知
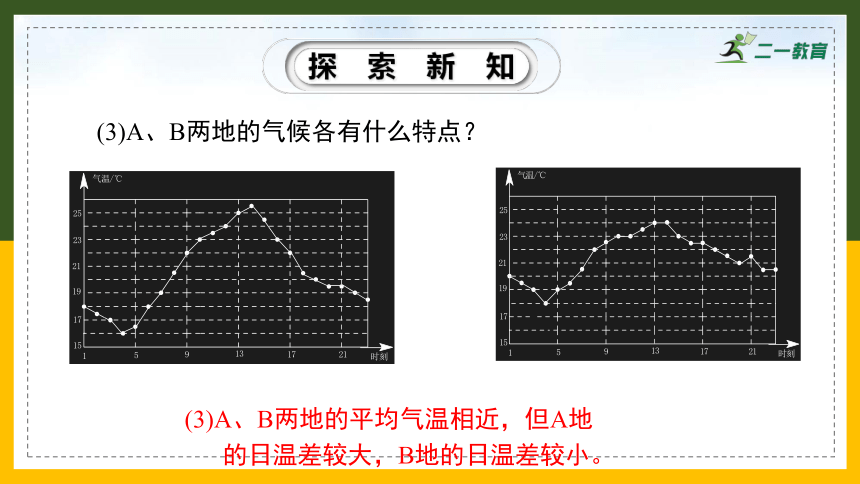
(3)A、B两地的气候各有什么特点?
(3)A、B两地的平均气温相近,但A地
的日温差较大,B地的日温差较小。
探索新知
例1:我校准备挑选一名跳高运动员参加江东区中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
甲的平均成绩为169 cm,
乙的平均成绩为168 cm.
解:
探索新知
(2)哪名运动员的成绩更稳定?
(3)若预测,跳过165 cm(包含165 cm)就很可能获得冠军.该校为了获得冠军,可能选哪名运动员参赛?若预测跳过170 cm(包含170 cm)才能获得冠军呢?
探索新知
(2)s甲2=6,s乙2=31.5,所以甲运动员的成绩更稳定.
(3)若跳过165 cm(包含165 cm)就很可能获得冠军,则在这8次成绩中,甲8次都跳过了165 cm,而乙只有5次, 所以应选甲运动员参赛;若跳过170 cm(包含170 cm)才能获得冠军,则在这8次成绩中,甲只有3次跳过了170 cm,而乙有5次,所以应选乙运动员参赛.
解:
探索新知
例2:农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到
各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
探索新知
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
探索新知
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
产量波动较大
产量波动较小
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
甲种甜玉米的产量
乙种甜玉米的产量
探索新知
②统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
方差越大,数据的波动越大;方差越小,数据的波动越小.
探索新知
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
两组数据的方差分别是:
探索新知
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
据样本估计总体的统计思想,种乙种甜玉米产量较
稳定.
显然 > ,即说明甲种甜玉米的波动较大,这与
我们从产量分布图看到的结果一致.
总结归纳
探索新知
(1)方差是用来衡量一组数据的波动大小的重要量,
反映的是数据在平均数附近波动的情况;
(2)对于同类问题的两组数据,方差越大,数据的波
动就越大;方差越小,数据的波动就越小;
(3)方差也不一定都是越小越好的,还需要具体问题
具体分析。
当堂检测
1.某排球队6名场上队员的身高(单位:cm)分别是:180,
184,188,190,192,194,现用一名身高为186 cm的队
员换下场上身高为192 cm的队员,与换人前相比,场上队
员的身高( A )
A
A. 平均数变小,方差变小 B. 平均数变小,方差不变
C. 平均数变大,方差变小 D. 平均数变大,方差不变
当堂检测
2.已知一组数据 x1, x2, x3, x4, x5的平均数是4,方差是
6,则3 x1+4,3 x2+4,3 x3+4,3 x4+4,3 x5+4的平均
数和方差分别为( D )
A. 4,6 B. 16,6
C. 4,22 D. 16,54
D
当堂检测
3.某学校对八年级(1)(2)两个班级的学生进行了一次数学测
试,两个班级前5名的成绩(满分:100分)分别是:
八(1)班:92分,86分,85分,85分,77分;
八(2)班:92分,89分,85分,85分,79分.
两个班级前5名的成绩的有关统计数据如下表.
平均分/分 中位数/分 众数/分 方差/分2
八(1)班 85 b c 22.8
八(2)班 a 85 85 19.2
当堂检测
(1) a = , b = , c = ;
点拨: a = =86,八(1)班前5名的成绩按从小到大的顺序排列为77分,85分,85分,86分,92分,
所以 b =85, c =85.
86
85
85
请解决下面问题:
当堂检测
(2)根据统计数据,说明哪个班级前5名的整体成绩较好.
解:因为八(2)班前5名的成绩的平均分大于八(1)班,而方差小于八(1)班,所以八(2)班前5名的平均成绩比八(1)班好,且成绩更稳定.所以八(2)班前5名的整体成绩较好.
当堂检测
4.如今,绿色轻简化突破性水稻新品种成为粮食培育发展的方向,某水稻试验基地为研究出优质高效、绿色轻简的水稻新品种,引进了甲、乙两种水稻良种,并同时在6块试验田进行播种培育,其产量(kg/亩)如下表所示:
试验田编号 ① ② ③ ④ ⑤ ⑥
甲 570 565 535 534 520 515
乙 550 540 550 540 545 515
当堂检测
现对甲、乙两种水稻良种粮食产量数据分析如下:
统计量 平均数(kg/亩) 中位数(kg/亩) 方差
甲 539.8 534.5 435.1
乙 540.0 m 141. 7
根据上述信息,解答下列问题:
(1)甲种水稻的试验田中,产量超过534.5 kg/亩的占比
为 %.
50
当堂检测
(2)求表格中的 m 及乙种水稻产量的众数.
解:(2)将乙种水稻6块试验田的水稻产量(kg/亩)从低到高排列为515,540,540,545,550,550,处在最中间的两个数据分别为540,545,所以 m = =542.5.因为乙种水稻产量中,数据540和550都出现了两次,出现的次数都最多,所以乙种水稻产量的众数为540 kg/亩和550 kg/亩.
当堂检测
(3)如果你是水稻培育员,要在这两种水稻良种中选择更具有
培育前景的一种,你会选择哪一种?为什么?
解:(3)选择乙.理由如下:
从平均数来看,乙的平均数比甲的高,说明乙的产量比甲的高;从方差来看,乙的方差比甲小,说明乙的产量稳定性更好,所以应该选择乙.
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
(3)方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
感谢收看
第六章 数据的分析
6.4.2数据的离散程度(2)
北师大版 数学 八年级 上册
学习目标
1.进一步了解极差、方差、标准差的求法.
2.会用极差、方差、标准差对实际问题做出判断.
情景导入
答: 一组数据中的最大值减去最小值所得的差叫做这组数据的极差.
1.哪些统计量可表示一组数据的集中趋势
答:一组数据的集中趋势可由平均数,众数,中位数表示
2.何为一组数据的极差
情景导入
3.极差反映了这组数据哪方面的特征
答:极差反映的是这组数据的变化范围或变化幅度.
4.极差有什么局限性
答:极差受极端值的影响较大,不能准确反映数据
的波动情况.
探索新知
方差的应用
一
如图是某一天A、B两地的气温变化图,回答问题:
(1)这一天A、B两地的平均气温分别是多少?
解:(1)A地的平均气温是20.42℃,
B地的平均气温是21.35℃;
探索新知
(2)A地这一天气温的极差、方差分别是多少?B地呢?
(2)A地的极差是9.5℃,方差是7.76,
B地的极差是6℃,方差是2.78;
探索新知
(3)A、B两地的气候各有什么特点?
(3)A、B两地的平均气温相近,但A地
的日温差较大,B地的日温差较小。
探索新知
例1:我校准备挑选一名跳高运动员参加江东区中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
甲的平均成绩为169 cm,
乙的平均成绩为168 cm.
解:
探索新知
(2)哪名运动员的成绩更稳定?
(3)若预测,跳过165 cm(包含165 cm)就很可能获得冠军.该校为了获得冠军,可能选哪名运动员参赛?若预测跳过170 cm(包含170 cm)才能获得冠军呢?
探索新知
(2)s甲2=6,s乙2=31.5,所以甲运动员的成绩更稳定.
(3)若跳过165 cm(包含165 cm)就很可能获得冠军,则在这8次成绩中,甲8次都跳过了165 cm,而乙只有5次, 所以应选甲运动员参赛;若跳过170 cm(包含170 cm)才能获得冠军,则在这8次成绩中,甲只有3次跳过了170 cm,而乙有5次,所以应选乙运动员参赛.
解:
探索新知
例2:农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到
各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
探索新知
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
探索新知
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
产量波动较大
产量波动较小
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
甲种甜玉米的产量
乙种甜玉米的产量
探索新知
②统计学中常采用下面的做法来量化这组数据的波动大小:
设有n个数据x1,x2,…,xn,各数据与它们的平均
数 的差的平方分别是 ,
我们用这些值的平均数,即用
来衡量这组数据的波动大小,称它为这组数据的方差.
方差越大,数据的波动越大;方差越小,数据的波动越小.
探索新知
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
两组数据的方差分别是:
探索新知
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
③请利用方差公式分析甲、乙两种甜玉米的波动程度.
据样本估计总体的统计思想,种乙种甜玉米产量较
稳定.
显然 > ,即说明甲种甜玉米的波动较大,这与
我们从产量分布图看到的结果一致.
总结归纳
探索新知
(1)方差是用来衡量一组数据的波动大小的重要量,
反映的是数据在平均数附近波动的情况;
(2)对于同类问题的两组数据,方差越大,数据的波
动就越大;方差越小,数据的波动就越小;
(3)方差也不一定都是越小越好的,还需要具体问题
具体分析。
当堂检测
1.某排球队6名场上队员的身高(单位:cm)分别是:180,
184,188,190,192,194,现用一名身高为186 cm的队
员换下场上身高为192 cm的队员,与换人前相比,场上队
员的身高( A )
A
A. 平均数变小,方差变小 B. 平均数变小,方差不变
C. 平均数变大,方差变小 D. 平均数变大,方差不变
当堂检测
2.已知一组数据 x1, x2, x3, x4, x5的平均数是4,方差是
6,则3 x1+4,3 x2+4,3 x3+4,3 x4+4,3 x5+4的平均
数和方差分别为( D )
A. 4,6 B. 16,6
C. 4,22 D. 16,54
D
当堂检测
3.某学校对八年级(1)(2)两个班级的学生进行了一次数学测
试,两个班级前5名的成绩(满分:100分)分别是:
八(1)班:92分,86分,85分,85分,77分;
八(2)班:92分,89分,85分,85分,79分.
两个班级前5名的成绩的有关统计数据如下表.
平均分/分 中位数/分 众数/分 方差/分2
八(1)班 85 b c 22.8
八(2)班 a 85 85 19.2
当堂检测
(1) a = , b = , c = ;
点拨: a = =86,八(1)班前5名的成绩按从小到大的顺序排列为77分,85分,85分,86分,92分,
所以 b =85, c =85.
86
85
85
请解决下面问题:
当堂检测
(2)根据统计数据,说明哪个班级前5名的整体成绩较好.
解:因为八(2)班前5名的成绩的平均分大于八(1)班,而方差小于八(1)班,所以八(2)班前5名的平均成绩比八(1)班好,且成绩更稳定.所以八(2)班前5名的整体成绩较好.
当堂检测
4.如今,绿色轻简化突破性水稻新品种成为粮食培育发展的方向,某水稻试验基地为研究出优质高效、绿色轻简的水稻新品种,引进了甲、乙两种水稻良种,并同时在6块试验田进行播种培育,其产量(kg/亩)如下表所示:
试验田编号 ① ② ③ ④ ⑤ ⑥
甲 570 565 535 534 520 515
乙 550 540 550 540 545 515
当堂检测
现对甲、乙两种水稻良种粮食产量数据分析如下:
统计量 平均数(kg/亩) 中位数(kg/亩) 方差
甲 539.8 534.5 435.1
乙 540.0 m 141. 7
根据上述信息,解答下列问题:
(1)甲种水稻的试验田中,产量超过534.5 kg/亩的占比
为 %.
50
当堂检测
(2)求表格中的 m 及乙种水稻产量的众数.
解:(2)将乙种水稻6块试验田的水稻产量(kg/亩)从低到高排列为515,540,540,545,550,550,处在最中间的两个数据分别为540,545,所以 m = =542.5.因为乙种水稻产量中,数据540和550都出现了两次,出现的次数都最多,所以乙种水稻产量的众数为540 kg/亩和550 kg/亩.
当堂检测
(3)如果你是水稻培育员,要在这两种水稻良种中选择更具有
培育前景的一种,你会选择哪一种?为什么?
解:(3)选择乙.理由如下:
从平均数来看,乙的平均数比甲的高,说明乙的产量比甲的高;从方差来看,乙的方差比甲小,说明乙的产量稳定性更好,所以应该选择乙.
(1)方差怎样计算?
(2)你如何理解方差的意义?
方差越大,数据的波动越大;
方差越小,数据的波动越小.
(3)方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差
来判断它们的波动情况.
感谢收看
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
