北师大八上6.3从统计图分析数据的集中趋势
文档属性
| 名称 | 北师大八上6.3从统计图分析数据的集中趋势 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-10 15:02:30 | ||
图片预览









文档简介
(共32张PPT)
第六章 数据的分析
6.3从统计图分析数据的集中趋势
北师大版 数学 八年级 上册
学习目标
1.经历从统计图分析数据集中趋势的活动,建立数据直觉,发展几何直观;
2.能从条形统计图、扇形统计图等统计图中获取信息,求出或估计相关数据的平均数、中位数、众数.
情景导入
1.如何确定一组数据的平均数?
确定中位数,应先把这组数据按大小顺序排列,最中间位置的一个数据或最中间两个数据的平均数即为中位数.
奇数加1除以2,
偶数2n除以2,得n,那么中位数是第n和n+1个数的平均数
2.如何确定众数呢
找一组数据中出现次数最多的那个数据.
情景导入
我们学过的统计图都有哪些?各自的特点是什么呢?
折线统计图
特点:用一个单位长度表示一定的数量;用折线的上升或下降表示数量的多少和增减变化情况。
作用:既可表示各种数量的多少,又可反映出数量的增减变化趋势。
情景导入
条形统计图
特点:用一个单位长度表示一定的数量;用直条的长短来表示数量的多少。
作用:用于表示各个数量的多少。
我们学过的统计图都有哪些?各自的特点是什么呢?
情景导入
扇形统计图
特点:用一个圆的面积来表示总数;用圆内扇形的大小来表示占总数的百分比。
作用:可以清楚地表示出各个部分与总体的关系。
我们学过的统计图都有哪些?各自的特点是什么呢?
探索新知
从折线统计图分析数据的集中趋势
一
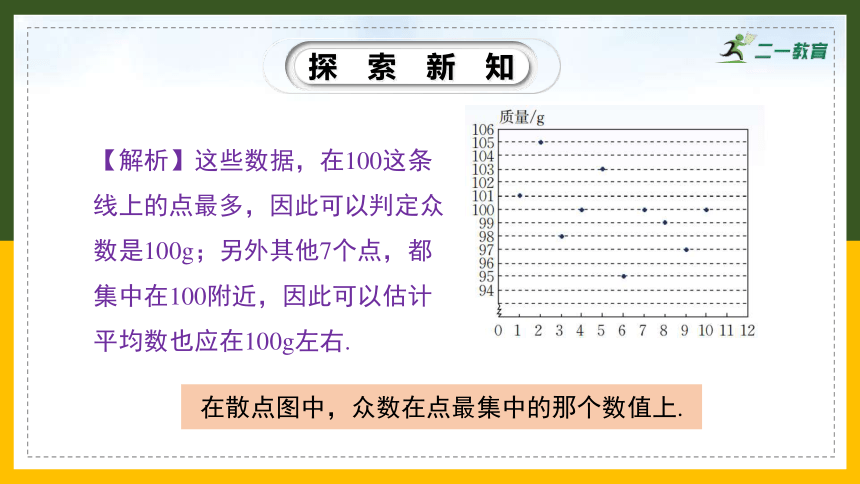
为了检查面包的质量是否达标,随机抽取同种规格的面包10个,这10个面包的质量如图所示.
这10个面包质量的众数是多少?你能估计出一个这样的面包的平均质量吗?你是怎么估计的?
探索新知
【解析】这些数据,在100这条线上的点最多,因此可以判定众数是100g;另外其他7个点,都集中在100附近,因此可以估计平均数也应在100g左右.
在散点图中,众数在点最集中的那个数值上.
探索新知
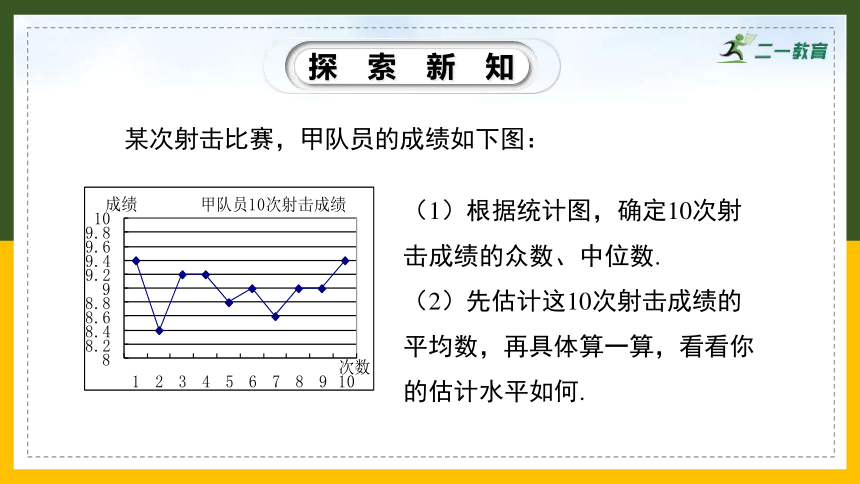
某次射击比赛,甲队员的成绩如下图:
(1)根据统计图,确定10次射击成绩的众数、中位数.
(2)先估计这10次射击成绩的平均数,再具体算一算,看看你的估计水平如何.
探索新知
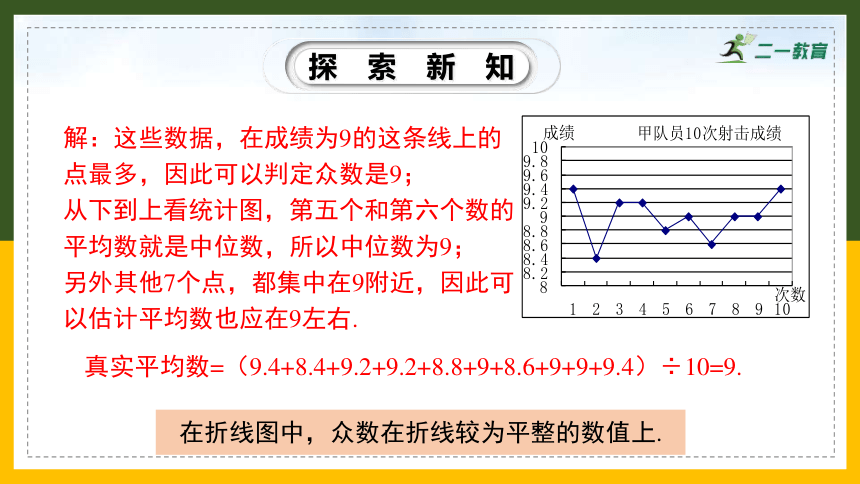
解:这些数据,在成绩为9的这条线上的点最多,因此可以判定众数是9;
从下到上看统计图,第五个和第六个数的平均数就是中位数,所以中位数为9;
另外其他7个点,都集中在9附近,因此可以估计平均数也应在9左右.
在折线图中,众数在折线较为平整的数值上.
真实平均数=(9.4+8.4+9.2+9.2+8.8+9+8.6+9+9+9.4)÷10=9.
总结归纳
探索新知
众数: __________________________________;
中位数:__________________________________________;
平均数: .
同一水平线上出现次数最多的数据
折线图上,从上到下(或从下到上)处于中间点所对应的数
可以用中位数与众数估测平均数.具体计算时可以以这个数为基准用简便算法求平均数.
在折线统计图中,可以怎样求一组数据的众数、中位数、平均数?
探索新知
从扇形统计图分析数据的集中趋势
二
(1)在这20位同学中,本学期计划购买课外书的花费的众数是多少?
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
50元在扇形图中所占面积最大,所以众数为50元.
探索新知
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
(2)计算这20位同学计划购买课外书的平均花费是多少?你是怎么计算的?
平均花费=100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
探索新知
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
答:这些百分比就是“权”平均花费为: 100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
(3)在上面的问题中,如果不知道调查的总人数,你还能求平均数吗?
探索新知
例:某地连续统计了10天日最高气温,并绘制成如下图所示的扇形统计图:
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
探索新知
解:(1)根据扇形统计图,35 ℃占的比重最大,因此日平均气温的众数是35 ℃.
(2)这10天日最高气温的平均值是:32×10%+33×20%+34×20%+35×30%+36×20%=34.3(℃).
探索新知
总结归纳
众数: _____________________________;
中位数:________________________________________;
平均数:____________________________.
面积最大的扇形所对应的数据
扇形图中各数据按大小顺序排列,相应的百分比 第50%、51%两个数据的平均数是中位数
可以利用加权平均数进行计算
在扇形统计图中,可以怎样求一组数据的众数、中位数、平均数?
探索新知
从条形统计图分析数据的集中趋势
三
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
(1)观察三幅图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
探索新知
解:(1) 从图中可以看出:
甲队队员年龄的众数是_____,中位数是_____;
乙队队员年龄的众数是_____,中位数是_____;
丙队队员年龄的众数是_____,中位数是_____.
20岁
20岁
19岁
19岁
21岁
21岁
在条形统计图中,众数是最高矩形所代表的值.
探索新知
解:(2)因为丙队队员年龄大的人数较多,所以估计丙队队员平均年龄最大,而乙队队员年龄大的人数较少,所以乙队队员平均年龄最小.
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?
探索新知
解:(3)甲:(18×1+19×3+20×4+21×3+22×1)÷12=20(岁);
乙: (18×3+19×5+20×2+21×1+22×1)÷12 ≈ 19.3(岁);
丙: (18×1+19×2+20×1+21×5+22×3)÷12≈ 20.6(岁).
(3)计算出三支球队队员的平均年龄,看看你上面的估计是否准确?
探索新知
总结归纳
在条形统计图中,可以怎样求一组数据的众数、中位数、平均数?
众数: _____________________________________;
中位数:__________________________________;
平均数:___________________________________.
柱子最高的小长方形所对应的数据
从左到右(或从右到左)找中间数
可以用中位数与众数估测平均数
当堂检测
1.如图是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,
下面关于该班50名同学一周锻炼时间的说法错误的是( )
C
A.众数是7时
B.中位数是6.5时
C.平均数是6.5时
D.平均每周锻炼时间超过6小时的人数占总人数的一半
当堂检测
2.如图是根据某班40名同学一周的体育锻炼情况
绘制的条形统计图,那么该班40名同学一周参加
体育锻炼时间的众数、中位数分别是( )
B
A.16, B.8,9 C.16, D.8,
当堂检测
3.小华班上比赛投篮,每人投6球,如图是班上所有学生投进
球数的扇形图.根据图形,下列关于班上所有学生投进球数
的统计量,正确的是( )
D
A.中位数为3 B.中位数为2.5
C.众数为5 D.众数为2
当堂检测
4.在“绿水青山,就是金山银山”的环保知识比赛中,某
校12名学生参赛成绩统计如图所示.下列说法错误的是
( )
C
A.众数是95 B.中位数是95
C.平均数是95 D.极差是15
当堂检测
5.在一次爱心捐款中,某班有40名学生捐了自己的零花钱,
有捐5元、10元、20元、50元的,如图反映了不同捐款钱
数的人数比例,那么这个班的学生平均每人捐款____元,捐
款___元的学生人数最多 ,捐款的中位数是___元.
16
5
5
当堂检测
6.在某市中小学生“人人会乐器”演奏比赛中,某班10名学
生成绩的统计图如图所示,则这10名学生成绩的平均数是
_____分 ,中位数是____分,众数是____分.
88.5
90
90
当堂检测
7.对某校八年级学生随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,共4个等级,将调查结果绘制成如图所示的条形统计图和扇形统计图.根据图中信息,求这些学生成绩的平均数、众数和中位数.
当堂检测
解:因为总人数为 (人),
4分的有12人,
3分的有 (人),
2分的有 (人),
1分的有3人,
所以中位数、众数都是3分.
平均分为 (分).
条形统计图
平均数:
众数:最高即为众数
中位数:从左往右看
折线统计图
扇形统计图
众数:同一水平线上出现次数最多
中位数:从上往下(或从下往上)看
平均数:
众数:扇形面积最大
中位数:数据排序,写出所对应的百分比,50%和 51%所对应数据的平均数
感谢收看
第六章 数据的分析
6.3从统计图分析数据的集中趋势
北师大版 数学 八年级 上册
学习目标
1.经历从统计图分析数据集中趋势的活动,建立数据直觉,发展几何直观;
2.能从条形统计图、扇形统计图等统计图中获取信息,求出或估计相关数据的平均数、中位数、众数.
情景导入
1.如何确定一组数据的平均数?
确定中位数,应先把这组数据按大小顺序排列,最中间位置的一个数据或最中间两个数据的平均数即为中位数.
奇数加1除以2,
偶数2n除以2,得n,那么中位数是第n和n+1个数的平均数
2.如何确定众数呢
找一组数据中出现次数最多的那个数据.
情景导入
我们学过的统计图都有哪些?各自的特点是什么呢?
折线统计图
特点:用一个单位长度表示一定的数量;用折线的上升或下降表示数量的多少和增减变化情况。
作用:既可表示各种数量的多少,又可反映出数量的增减变化趋势。
情景导入
条形统计图
特点:用一个单位长度表示一定的数量;用直条的长短来表示数量的多少。
作用:用于表示各个数量的多少。
我们学过的统计图都有哪些?各自的特点是什么呢?
情景导入
扇形统计图
特点:用一个圆的面积来表示总数;用圆内扇形的大小来表示占总数的百分比。
作用:可以清楚地表示出各个部分与总体的关系。
我们学过的统计图都有哪些?各自的特点是什么呢?
探索新知
从折线统计图分析数据的集中趋势
一
为了检查面包的质量是否达标,随机抽取同种规格的面包10个,这10个面包的质量如图所示.
这10个面包质量的众数是多少?你能估计出一个这样的面包的平均质量吗?你是怎么估计的?
探索新知
【解析】这些数据,在100这条线上的点最多,因此可以判定众数是100g;另外其他7个点,都集中在100附近,因此可以估计平均数也应在100g左右.
在散点图中,众数在点最集中的那个数值上.
探索新知
某次射击比赛,甲队员的成绩如下图:
(1)根据统计图,确定10次射击成绩的众数、中位数.
(2)先估计这10次射击成绩的平均数,再具体算一算,看看你的估计水平如何.
探索新知
解:这些数据,在成绩为9的这条线上的点最多,因此可以判定众数是9;
从下到上看统计图,第五个和第六个数的平均数就是中位数,所以中位数为9;
另外其他7个点,都集中在9附近,因此可以估计平均数也应在9左右.
在折线图中,众数在折线较为平整的数值上.
真实平均数=(9.4+8.4+9.2+9.2+8.8+9+8.6+9+9+9.4)÷10=9.
总结归纳
探索新知
众数: __________________________________;
中位数:__________________________________________;
平均数: .
同一水平线上出现次数最多的数据
折线图上,从上到下(或从下到上)处于中间点所对应的数
可以用中位数与众数估测平均数.具体计算时可以以这个数为基准用简便算法求平均数.
在折线统计图中,可以怎样求一组数据的众数、中位数、平均数?
探索新知
从扇形统计图分析数据的集中趋势
二
(1)在这20位同学中,本学期计划购买课外书的花费的众数是多少?
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
50元在扇形图中所占面积最大,所以众数为50元.
探索新知
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
(2)计算这20位同学计划购买课外书的平均花费是多少?你是怎么计算的?
平均花费=100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
探索新知
小明调查了班级里20位同学本学期计划购买课外书的花费情况,并将结果绘制成了下面的统计图:
答:这些百分比就是“权”平均花费为: 100×10%+80×25%+50×40%+30×20%+20×5%=57(元).
(3)在上面的问题中,如果不知道调查的总人数,你还能求平均数吗?
探索新知
例:某地连续统计了10天日最高气温,并绘制成如下图所示的扇形统计图:
(1)这10天中,日最高气温的众数是多少?
(2)计算这10天日最高气温的平均值.
探索新知
解:(1)根据扇形统计图,35 ℃占的比重最大,因此日平均气温的众数是35 ℃.
(2)这10天日最高气温的平均值是:32×10%+33×20%+34×20%+35×30%+36×20%=34.3(℃).
探索新知
总结归纳
众数: _____________________________;
中位数:________________________________________;
平均数:____________________________.
面积最大的扇形所对应的数据
扇形图中各数据按大小顺序排列,相应的百分比 第50%、51%两个数据的平均数是中位数
可以利用加权平均数进行计算
在扇形统计图中,可以怎样求一组数据的众数、中位数、平均数?
探索新知
从条形统计图分析数据的集中趋势
三
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
(1)观察三幅图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢?
探索新知
解:(1) 从图中可以看出:
甲队队员年龄的众数是_____,中位数是_____;
乙队队员年龄的众数是_____,中位数是_____;
丙队队员年龄的众数是_____,中位数是_____.
20岁
20岁
19岁
19岁
21岁
21岁
在条形统计图中,众数是最高矩形所代表的值.
探索新知
解:(2)因为丙队队员年龄大的人数较多,所以估计丙队队员平均年龄最大,而乙队队员年龄大的人数较少,所以乙队队员平均年龄最小.
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?
探索新知
解:(3)甲:(18×1+19×3+20×4+21×3+22×1)÷12=20(岁);
乙: (18×3+19×5+20×2+21×1+22×1)÷12 ≈ 19.3(岁);
丙: (18×1+19×2+20×1+21×5+22×3)÷12≈ 20.6(岁).
(3)计算出三支球队队员的平均年龄,看看你上面的估计是否准确?
探索新知
总结归纳
在条形统计图中,可以怎样求一组数据的众数、中位数、平均数?
众数: _____________________________________;
中位数:__________________________________;
平均数:___________________________________.
柱子最高的小长方形所对应的数据
从左到右(或从右到左)找中间数
可以用中位数与众数估测平均数
当堂检测
1.如图是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,
下面关于该班50名同学一周锻炼时间的说法错误的是( )
C
A.众数是7时
B.中位数是6.5时
C.平均数是6.5时
D.平均每周锻炼时间超过6小时的人数占总人数的一半
当堂检测
2.如图是根据某班40名同学一周的体育锻炼情况
绘制的条形统计图,那么该班40名同学一周参加
体育锻炼时间的众数、中位数分别是( )
B
A.16, B.8,9 C.16, D.8,
当堂检测
3.小华班上比赛投篮,每人投6球,如图是班上所有学生投进
球数的扇形图.根据图形,下列关于班上所有学生投进球数
的统计量,正确的是( )
D
A.中位数为3 B.中位数为2.5
C.众数为5 D.众数为2
当堂检测
4.在“绿水青山,就是金山银山”的环保知识比赛中,某
校12名学生参赛成绩统计如图所示.下列说法错误的是
( )
C
A.众数是95 B.中位数是95
C.平均数是95 D.极差是15
当堂检测
5.在一次爱心捐款中,某班有40名学生捐了自己的零花钱,
有捐5元、10元、20元、50元的,如图反映了不同捐款钱
数的人数比例,那么这个班的学生平均每人捐款____元,捐
款___元的学生人数最多 ,捐款的中位数是___元.
16
5
5
当堂检测
6.在某市中小学生“人人会乐器”演奏比赛中,某班10名学
生成绩的统计图如图所示,则这10名学生成绩的平均数是
_____分 ,中位数是____分,众数是____分.
88.5
90
90
当堂检测
7.对某校八年级学生随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分,共4个等级,将调查结果绘制成如图所示的条形统计图和扇形统计图.根据图中信息,求这些学生成绩的平均数、众数和中位数.
当堂检测
解:因为总人数为 (人),
4分的有12人,
3分的有 (人),
2分的有 (人),
1分的有3人,
所以中位数、众数都是3分.
平均分为 (分).
条形统计图
平均数:
众数:最高即为众数
中位数:从左往右看
折线统计图
扇形统计图
众数:同一水平线上出现次数最多
中位数:从上往下(或从下往上)看
平均数:
众数:扇形面积最大
中位数:数据排序,写出所对应的百分比,50%和 51%所对应数据的平均数
感谢收看
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
