第5章轴对称与旋转全章复习课件(共29张PPT)
文档属性
| 名称 | 第5章轴对称与旋转全章复习课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-01 17:00:14 | ||
图片预览




文档简介
课件29张PPT。第5章 轴对称与旋转
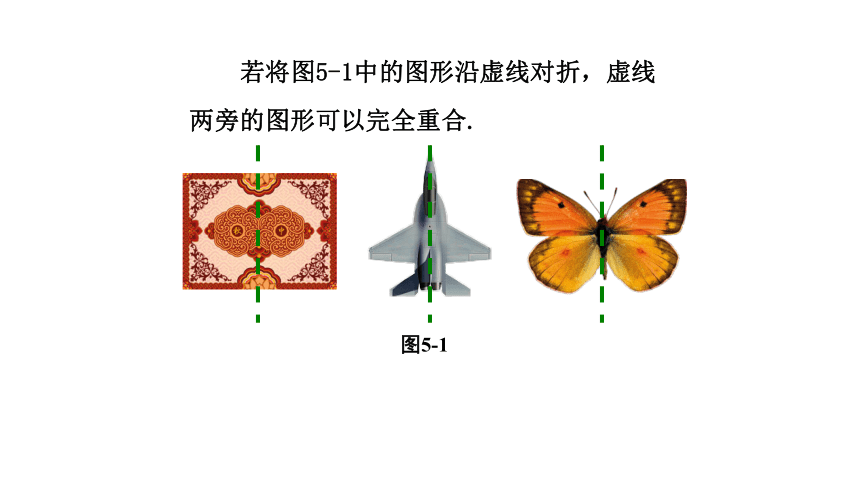
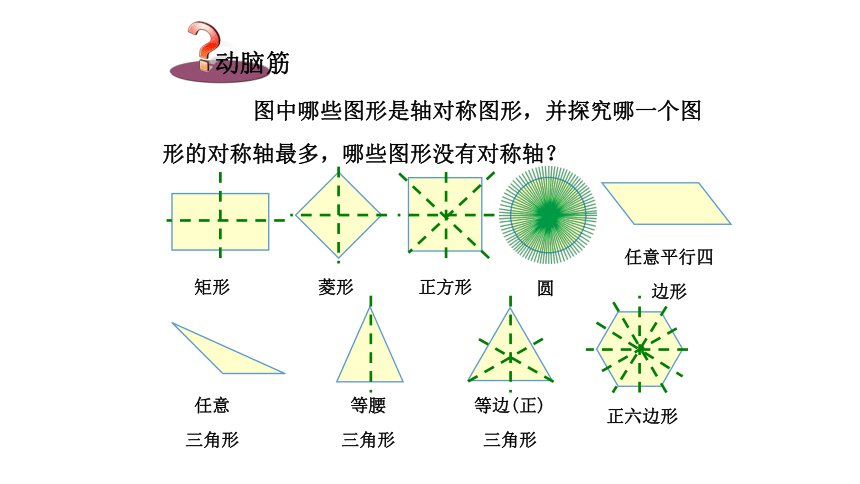
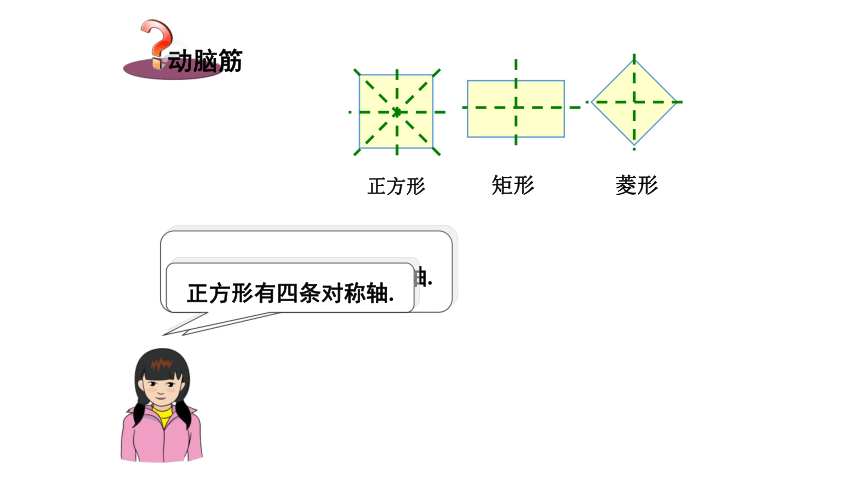
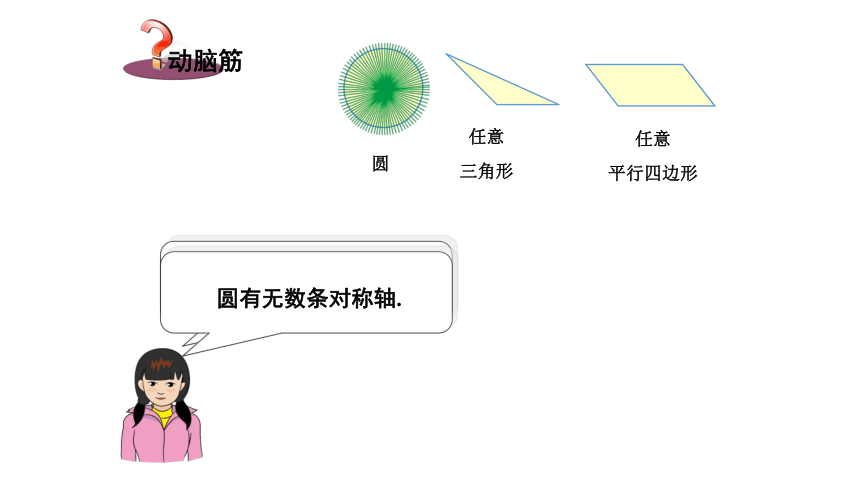
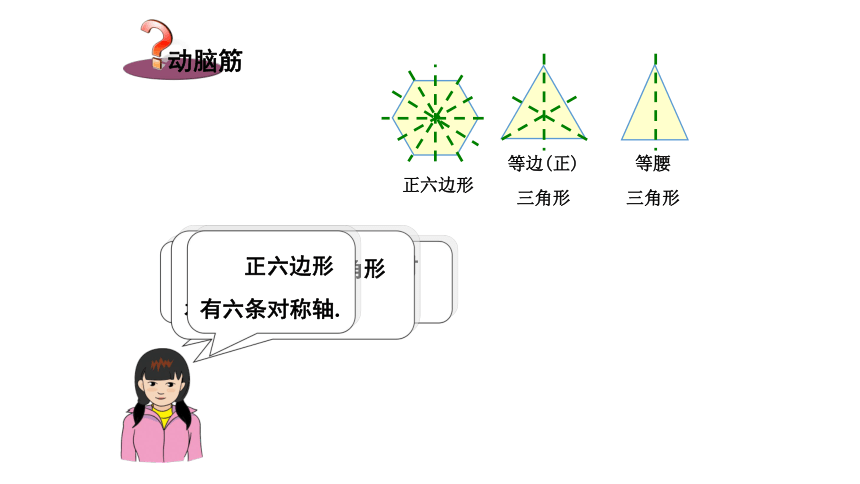
章末复习湘教版 七年级下册图中的故宫、天坛以及图5-1中的窗花、飞机和蝴蝶的平面图形,它们展示给我们的是和谐优美的形象.图5-1复习回顾轴对称图形图5-1图5-1中的窗花、飞机和蝴蝶的平面图形,你能发现它们有什么共同的特征吗? 若将图5-1中的图形沿虚线对折,虚线两旁的图形可以完全重合. 图5-1如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴. 图中哪些图形是轴对称图形,并探究哪一个图形的对称轴最多,哪些图形没有对称轴?矩形和菱形有两条对称轴.正方形有四条对称轴. 任意三角形和任意平行四边形没有对称轴. 圆有无数条对称轴. 等腰三角形有一条对称轴. 等边(正)三角形有三条对称轴. 正六边形有六条对称轴. 如图,用印章在一张纸上盖上一个印(a),趁印迹未干之时,将纸张对折得到印(b),随后打开,观察图形(a)与(b)会有怎样的关系.轴对称变换 把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换,也叫轴反射.图形(a)叫做原像,图形(b)叫做图形(a)在这个轴反射下的像. 如果一个图形关于某一条直线做轴对称变换后,能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称这两个图形成轴对称.这条直线叫做对称轴.原像与像中能互相重合的两个点,其中一点叫做另一个点关于这条直线的对应点. 图中,对称轴两边的图形(a)与(b)的形状和大小发生变化了吗?我们从图中可以看出,轴对称变换具有下述性质: 轴对称变换不改变图形的形状与大小. 例如:长度、角度和面积等都不改变. 把成轴对称的两个图形看成一个整体,它就是一个轴对称图形; 把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线轴对称.如图,三角形 ABC 和三角形A'B'C'关于直线 l 成轴对称,点P和P '是对应点,线段PP'交直线l 于点D. 那么线段 PP'与对称轴 l 有什么关系呢?因为三角形ABC 和三角形A'B'C'关于直线 l成轴对称,将图 5-5沿直线l折叠,则点P与P'重合,所以PD与P'D ,∠1与∠2也互相重合,故有PD=P'D ,∠1=∠2=90o,因此,l⊥PP', 且平分PP',即直线 l垂直平分线段 PP '.成轴对称的两个图形中,对应点的连线被对称轴垂直平分.例1 如图,已知直线 l 及直线外一点P,求作点P',使它与点P关于直线l对称.作法:
1. 过点P作 PQ⊥l,交l于点 O.
2. 在直线 PQ上,截取 OP'=OP.
则点P'即为所求作的点..POP'lQ典例精析例2 如图,已知三角形ABC和直线l,作出与三角形 ABC关于直线l对称的图形.分析:要作三角形ABC关于直线l的对称图形,只要作出三角形的顶点A,B,C关于直线l的对应点A',B',C',连接这些对应点,得到的三角形A'B'C'就是三角形ABC 关于直线l对称的图形.作法:
1. 过点A作直线l的垂线,垂足为点O,在垂线上截取OA'= OA,点A'就是点A关于直线l的对应点.
2. 类似地,分别作出点B,C关于直线l的对应点 B',C'.
3. 连接A'B',B'C',C'A'得到的三角形A'B'C'即为所求.画好三角形 A'B'C'后,若将纸沿直线l对折两个三角形会重合吗? 观察钟表的指针,电风扇的叶片,在转动的过程中有什么共同的特征. 钟表的指针绕中间的固定点旋转,电风扇的叶片绕电机的轴旋转.旋转将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转角α),得到图形F',如图,图形的这种变换叫做旋转.这个定点 O 叫旋转中心,角α叫做旋转角.原位置的图形F叫做原像, 新位置的图形 F'叫做图形F在旋转下的像.图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.图5-12如图,将三角形ABC按逆时针方向绕点O旋转60o得到三角形A'B'C',三角形ABC内的点P在这个旋转下的像是点P',则OA'与OA相等吗?∠POP'和∠AOA'相等吗?度数等于多少?ABCA'B'C'O..P 'P 60o由旋转的概念可得,OA与OA'相等.
由旋转的概念可得,∠POP'=60o=∠AOA'.ABCB'C'O..P 'P 60o 一个图形和它经过旋转所得到的图形中, 对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角相等.旋转具有下述性质:在图中,当三角形ABC旋转到新的位置,得到三角形A'B'C',它的形状和大小发生变化了吗?旋转具有下述性质:旋转不改变图形的形状和大小 .通过这节课的学习活动,你有什么收获?课堂小结1.从课后习题中选取;
2.完成练习册本课时的习题。课后作业
章末复习湘教版 七年级下册图中的故宫、天坛以及图5-1中的窗花、飞机和蝴蝶的平面图形,它们展示给我们的是和谐优美的形象.图5-1复习回顾轴对称图形图5-1图5-1中的窗花、飞机和蝴蝶的平面图形,你能发现它们有什么共同的特征吗? 若将图5-1中的图形沿虚线对折,虚线两旁的图形可以完全重合. 图5-1如果一个图形沿着一条直线折叠,直线两侧的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做它的对称轴. 图中哪些图形是轴对称图形,并探究哪一个图形的对称轴最多,哪些图形没有对称轴?矩形和菱形有两条对称轴.正方形有四条对称轴. 任意三角形和任意平行四边形没有对称轴. 圆有无数条对称轴. 等腰三角形有一条对称轴. 等边(正)三角形有三条对称轴. 正六边形有六条对称轴. 如图,用印章在一张纸上盖上一个印(a),趁印迹未干之时,将纸张对折得到印(b),随后打开,观察图形(a)与(b)会有怎样的关系.轴对称变换 把图形(a)沿着直线l翻折并将图形“复印”下来得到图形(b),就叫做该图形关于直线l作了轴对称变换,也叫轴反射.图形(a)叫做原像,图形(b)叫做图形(a)在这个轴反射下的像. 如果一个图形关于某一条直线做轴对称变换后,能够与另一个图形重合,那么就说这两个图形关于这条直线对称,也称这两个图形成轴对称.这条直线叫做对称轴.原像与像中能互相重合的两个点,其中一点叫做另一个点关于这条直线的对应点. 图中,对称轴两边的图形(a)与(b)的形状和大小发生变化了吗?我们从图中可以看出,轴对称变换具有下述性质: 轴对称变换不改变图形的形状与大小. 例如:长度、角度和面积等都不改变. 把成轴对称的两个图形看成一个整体,它就是一个轴对称图形; 把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条直线轴对称.如图,三角形 ABC 和三角形A'B'C'关于直线 l 成轴对称,点P和P '是对应点,线段PP'交直线l 于点D. 那么线段 PP'与对称轴 l 有什么关系呢?因为三角形ABC 和三角形A'B'C'关于直线 l成轴对称,将图 5-5沿直线l折叠,则点P与P'重合,所以PD与P'D ,∠1与∠2也互相重合,故有PD=P'D ,∠1=∠2=90o,因此,l⊥PP', 且平分PP',即直线 l垂直平分线段 PP '.成轴对称的两个图形中,对应点的连线被对称轴垂直平分.例1 如图,已知直线 l 及直线外一点P,求作点P',使它与点P关于直线l对称.作法:
1. 过点P作 PQ⊥l,交l于点 O.
2. 在直线 PQ上,截取 OP'=OP.
则点P'即为所求作的点..POP'lQ典例精析例2 如图,已知三角形ABC和直线l,作出与三角形 ABC关于直线l对称的图形.分析:要作三角形ABC关于直线l的对称图形,只要作出三角形的顶点A,B,C关于直线l的对应点A',B',C',连接这些对应点,得到的三角形A'B'C'就是三角形ABC 关于直线l对称的图形.作法:
1. 过点A作直线l的垂线,垂足为点O,在垂线上截取OA'= OA,点A'就是点A关于直线l的对应点.
2. 类似地,分别作出点B,C关于直线l的对应点 B',C'.
3. 连接A'B',B'C',C'A'得到的三角形A'B'C'即为所求.画好三角形 A'B'C'后,若将纸沿直线l对折两个三角形会重合吗? 观察钟表的指针,电风扇的叶片,在转动的过程中有什么共同的特征. 钟表的指针绕中间的固定点旋转,电风扇的叶片绕电机的轴旋转.旋转将一个平面图形F上的每一个点,绕这个平面内一定点O旋转同一个角α,(即把图形F上每一个点与定点的连线绕定点O旋转角α),得到图形F',如图,图形的这种变换叫做旋转.这个定点 O 叫旋转中心,角α叫做旋转角.原位置的图形F叫做原像, 新位置的图形 F'叫做图形F在旋转下的像.图形F上的每一个点P与它在旋转下的像点P'叫做在旋转下的对应点.图5-12如图,将三角形ABC按逆时针方向绕点O旋转60o得到三角形A'B'C',三角形ABC内的点P在这个旋转下的像是点P',则OA'与OA相等吗?∠POP'和∠AOA'相等吗?度数等于多少?ABCA'B'C'O..P 'P 60o由旋转的概念可得,OA与OA'相等.
由旋转的概念可得,∠POP'=60o=∠AOA'.ABCB'C'O..P 'P 60o 一个图形和它经过旋转所得到的图形中, 对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角相等.旋转具有下述性质:在图中,当三角形ABC旋转到新的位置,得到三角形A'B'C',它的形状和大小发生变化了吗?旋转具有下述性质:旋转不改变图形的形状和大小 .通过这节课的学习活动,你有什么收获?课堂小结1.从课后习题中选取;
2.完成练习册本课时的习题。课后作业
