人教版八年级下册第十七章 勾股定理的复习 教学设计(表格式)
文档属性
| 名称 | 人教版八年级下册第十七章 勾股定理的复习 教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 148.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 20:31:05 | ||
图片预览

文档简介
教学设计
课题 勾股定理的复习
课型 复习课
教学内容分析直角三角形是特殊的三角形,它的三边之间有特殊的数量关系,本章通过对面积关系的探究,发现并证明了勾股定理.勾股定理是直角三角形三边关系的描述,不仅在解决与直角三角形相关的问题时很有用,而且在解决其它许多数学问题时也很有用.得到一个数学结论后,经常要研究其逆命题是否成立,一般地,原命题成立,逆命题未必成立,勾股定理的逆定理成立,它提供了一种直角三角形的判定方法,是从相反的路径对直角三角形进行了刻画.
学情分析学生通过本章的学习过程,已经学习了勾股定理及其逆定理的内容,在上一阶段的学习中也能够用两个定理解决一些问题。本节课要求学生能够将本章的知识内容形成体系,选择适当的定理,并结合分类讨论,方程思想等数学思想综合的解决问题,对学生的要求较高。
学习目标1.按照本章知识的呈现顺序,梳理勾股定理及其逆定理的相关概念.2.能够根据具体题目背景综合运用勾股定理及其逆定理解决问题.难点:能够综合运用勾股定理及其逆定理解决问题。
重难点1.按照本章知识的呈现顺序,梳理勾股定理及其逆定理的相关概念.2.能够根据具体题目背景综合运用勾股定理及其逆定理解决问题.
评价任务目标达成的标志是能够明确勾股定理及其逆定理的内容及关系,能够体会互逆命题与互逆定理之间的联系,在实际背景和几何问题中能够灵活运用勾股定理及其逆定理的数学思想方法解决综合问题.
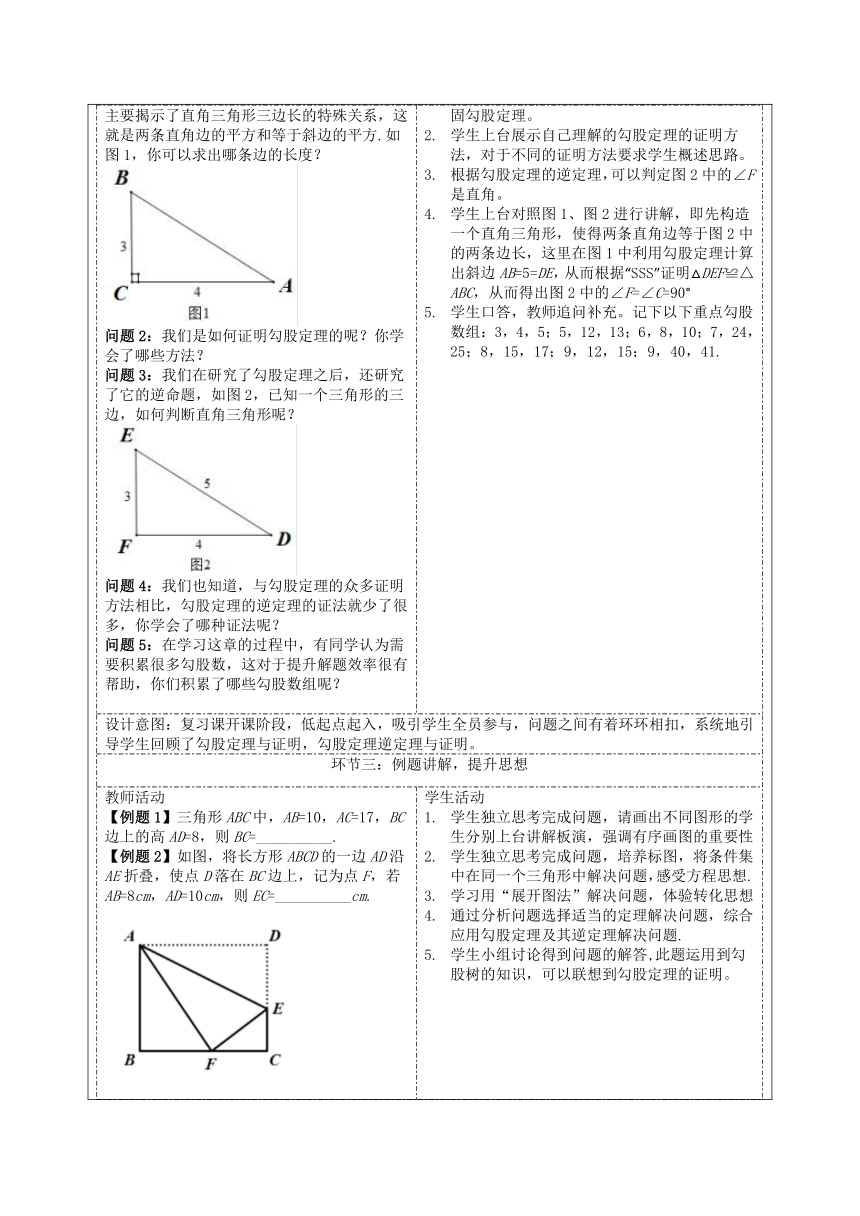
教学评活动过程教师活动学生活动环节一:课前检测 教师活动1.一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )A. 13 B. 5 或13 C. 5 D. 42.下列四条线段不能组成直角三角形的是( )A.a=8,b=15,c=17;B.a=9,b=12,c=15;C.a=,b=,c=;D.a:b:c=2:3:4.3.下列定理中,其逆命题是假命题的是( )A.两直线平行,内错角相等 B.对顶角相等C.等腰三角形的两个底角相等 D.等边三角形的三个内角都是60°合适的时间后展示出正确答案。学生活动学生快速完成,按照答案自评。设计意图:第一个问题对学生是否知道勾股定理的内容做检测;第二个问题考查学生对勾股定理的逆定理的理解;第三个问题考查学生对互逆命题的理解. 环节二:知识复习,巩固基础教师活动问题1:本章我们学习了勾股定理,勾股定理主要揭示了直角三角形三边长的特殊关系,这就是两条直角边的平方和等于斜边的平方.如图1,你可以求出哪条边的长度?问题2:我们是如何证明勾股定理的呢?你学会了哪些方法?问题3:我们在研究了勾股定理之后,还研究了它的逆命题,如图2,已知一个三角形的三边,如何判断直角三角形呢?问题4:我们也知道,与勾股定理的众多证明方法相比,勾股定理的逆定理的证法就少了很多,你学会了哪种证法呢?问题5:在学习这章的过程中,有同学认为需要积累很多勾股数,这对于提升解题效率很有帮助,你们积累了哪些勾股数组呢?学生活动学生口答出AB=5之后,一个学生说明过程,巩固勾股定理。学生上台展示自己理解的勾股定理的证明方法,对于不同的证明方法要求学生概述思路。根据勾股定理的逆定理,可以判定图2中的∠F是直角。学生上台对照图1、图2进行讲解,即先构造一个直角三角形,使得两条直角边等于图2中的两条边长,这里在图1中利用勾股定理计算出斜边AB=5=DE,从而根据“SSS”证明△DEF≌△ABC,从而得出图2中的∠F=∠C=90°学生口答,教师追问补充。记下以下重点勾股数组:3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,12,15;9,40,41.设计意图:复习课开课阶段,低起点起入,吸引学生全员参与,问题之间有着环环相扣,系统地引导学生回顾了勾股定理与证明,勾股定理逆定理与证明。环节三:例题讲解,提升思想教师活动【例题1】三角形ABC中,AB=10,AC=17,BC边上的高AD=8,则BC=__________.【例题2】如图,将长方形ABCD的一边AD沿AE折叠,使点D落在BC边上,记为点F,若AB=8cm,AD=10cm,则EC=__________cm.【例题3】一个圆柱高为8cm,底面直径为4cm,沿着圆柱表面从点A到点B的最短路程是__________cm.(π取3)【例题4】小区里有一块四边形的绿化带,∠B=900,AB=3,BC=4,CD=12,AD=13,求绿化带的面积.【例题5】Rt△ABC中,∠ACB=90°,AC=5,BC=12,分别以它的三边为直径向上作三个半圆,则阴影部分面积为__________.学生活动学生独立思考完成问题,请画出不同图形的学生分别上台讲解板演,强调有序画图的重要性学生独立思考完成问题,培养标图,将条件集中在同一个三角形中解决问题,感受方程思想.学习用“展开图法”解决问题,体验转化思想通过分析问题选择适当的定理解决问题,综合应用勾股定理及其逆定理解决问题.学生小组讨论得到问题的解答,此题运用到勾股树的知识,可以联想到勾股定理的证明。设计意图:几个例题分别对应不同的专题类型,从折叠专题到最短路径,最终都是勾股定理及其逆定理的综合运用,这些题目之间既有区别也互相联系,层层递进,提高学生的分析能力和解决问题的能力。环节四:归纳小结教师活动教师引导学生对以下问题进行反思,回顾本节课内容:1.今天我们复习了哪些知识,它们又怎么样的关系?2.解决数学问题的过程中你会注意哪些问题?体会到了哪些数学思想?学生活动学生畅所欲言,分享自己的收获与体验。设计意图:引导学生回顾勾股定理及其逆定理,明确其基本应用.引导学生回顾和体会解题的思路和数学思想方法.环节五:达标检测教师活动给出题目:一、选择题1.已知直角三角形两边的长分别为5、12,则第三边的长为( )A. 13 B. 60 C. 17 D. 13或2.下列条件中,不能判断△ABC为直角三角形的是( )A. a=1.5 b=2 c=2.5 B. a:b:c=5:12:13C. ∠A+∠B=∠C D. ∠A:∠B:∠C=3:4:5二、填空题3.写出定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:___________.4.如图小方格都是边长为1的正方形,则四边形ABCD的面积是___________.学生活动独立完成设计意图:测试学生目标达成情况。
板书设计勾股定理及其逆定理例题解题思路。学生板演过程
作业与拓展学习设计必做题:教材38页第8,9,10题选做题:教材39页第14题。
特色学习资源分析、技术手段应用说明(结合教学特色和实际撰写)借助《几何画板》工具演示立体图形展开成平面图形过程中对应点的关系,帮助学生理解最短路径问题.PPT展示课件,方便大量例题与习题的呈现。希沃展台的使用更快地呈现许多学生练习过程。
教学反思与改进本节课要求学生能够将本章的知识内容形成体系,选择适当的定理,并结合分类讨论,方程思想等数学思想综合的解决问题,对学生的要求较高.学生可能在性质和判定的使用上存在障碍,不能够综合地分析问题,选择最优化的解决问题的途径.应对策略在教学中,应该注意强调勾股定理及其逆定理的作用的不同,理清解决几何问题和实际问题所需要的必备的条件中是需要直角还是已知直角求边长,从而综合并且熟练地使用勾股定理及其逆定理.
课题 勾股定理的复习
课型 复习课
教学内容分析直角三角形是特殊的三角形,它的三边之间有特殊的数量关系,本章通过对面积关系的探究,发现并证明了勾股定理.勾股定理是直角三角形三边关系的描述,不仅在解决与直角三角形相关的问题时很有用,而且在解决其它许多数学问题时也很有用.得到一个数学结论后,经常要研究其逆命题是否成立,一般地,原命题成立,逆命题未必成立,勾股定理的逆定理成立,它提供了一种直角三角形的判定方法,是从相反的路径对直角三角形进行了刻画.
学情分析学生通过本章的学习过程,已经学习了勾股定理及其逆定理的内容,在上一阶段的学习中也能够用两个定理解决一些问题。本节课要求学生能够将本章的知识内容形成体系,选择适当的定理,并结合分类讨论,方程思想等数学思想综合的解决问题,对学生的要求较高。
学习目标1.按照本章知识的呈现顺序,梳理勾股定理及其逆定理的相关概念.2.能够根据具体题目背景综合运用勾股定理及其逆定理解决问题.难点:能够综合运用勾股定理及其逆定理解决问题。
重难点1.按照本章知识的呈现顺序,梳理勾股定理及其逆定理的相关概念.2.能够根据具体题目背景综合运用勾股定理及其逆定理解决问题.
评价任务目标达成的标志是能够明确勾股定理及其逆定理的内容及关系,能够体会互逆命题与互逆定理之间的联系,在实际背景和几何问题中能够灵活运用勾股定理及其逆定理的数学思想方法解决综合问题.
教学评活动过程教师活动学生活动环节一:课前检测 教师活动1.一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )A. 13 B. 5 或13 C. 5 D. 42.下列四条线段不能组成直角三角形的是( )A.a=8,b=15,c=17;B.a=9,b=12,c=15;C.a=,b=,c=;D.a:b:c=2:3:4.3.下列定理中,其逆命题是假命题的是( )A.两直线平行,内错角相等 B.对顶角相等C.等腰三角形的两个底角相等 D.等边三角形的三个内角都是60°合适的时间后展示出正确答案。学生活动学生快速完成,按照答案自评。设计意图:第一个问题对学生是否知道勾股定理的内容做检测;第二个问题考查学生对勾股定理的逆定理的理解;第三个问题考查学生对互逆命题的理解. 环节二:知识复习,巩固基础教师活动问题1:本章我们学习了勾股定理,勾股定理主要揭示了直角三角形三边长的特殊关系,这就是两条直角边的平方和等于斜边的平方.如图1,你可以求出哪条边的长度?问题2:我们是如何证明勾股定理的呢?你学会了哪些方法?问题3:我们在研究了勾股定理之后,还研究了它的逆命题,如图2,已知一个三角形的三边,如何判断直角三角形呢?问题4:我们也知道,与勾股定理的众多证明方法相比,勾股定理的逆定理的证法就少了很多,你学会了哪种证法呢?问题5:在学习这章的过程中,有同学认为需要积累很多勾股数,这对于提升解题效率很有帮助,你们积累了哪些勾股数组呢?学生活动学生口答出AB=5之后,一个学生说明过程,巩固勾股定理。学生上台展示自己理解的勾股定理的证明方法,对于不同的证明方法要求学生概述思路。根据勾股定理的逆定理,可以判定图2中的∠F是直角。学生上台对照图1、图2进行讲解,即先构造一个直角三角形,使得两条直角边等于图2中的两条边长,这里在图1中利用勾股定理计算出斜边AB=5=DE,从而根据“SSS”证明△DEF≌△ABC,从而得出图2中的∠F=∠C=90°学生口答,教师追问补充。记下以下重点勾股数组:3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,12,15;9,40,41.设计意图:复习课开课阶段,低起点起入,吸引学生全员参与,问题之间有着环环相扣,系统地引导学生回顾了勾股定理与证明,勾股定理逆定理与证明。环节三:例题讲解,提升思想教师活动【例题1】三角形ABC中,AB=10,AC=17,BC边上的高AD=8,则BC=__________.【例题2】如图,将长方形ABCD的一边AD沿AE折叠,使点D落在BC边上,记为点F,若AB=8cm,AD=10cm,则EC=__________cm.【例题3】一个圆柱高为8cm,底面直径为4cm,沿着圆柱表面从点A到点B的最短路程是__________cm.(π取3)【例题4】小区里有一块四边形的绿化带,∠B=900,AB=3,BC=4,CD=12,AD=13,求绿化带的面积.【例题5】Rt△ABC中,∠ACB=90°,AC=5,BC=12,分别以它的三边为直径向上作三个半圆,则阴影部分面积为__________.学生活动学生独立思考完成问题,请画出不同图形的学生分别上台讲解板演,强调有序画图的重要性学生独立思考完成问题,培养标图,将条件集中在同一个三角形中解决问题,感受方程思想.学习用“展开图法”解决问题,体验转化思想通过分析问题选择适当的定理解决问题,综合应用勾股定理及其逆定理解决问题.学生小组讨论得到问题的解答,此题运用到勾股树的知识,可以联想到勾股定理的证明。设计意图:几个例题分别对应不同的专题类型,从折叠专题到最短路径,最终都是勾股定理及其逆定理的综合运用,这些题目之间既有区别也互相联系,层层递进,提高学生的分析能力和解决问题的能力。环节四:归纳小结教师活动教师引导学生对以下问题进行反思,回顾本节课内容:1.今天我们复习了哪些知识,它们又怎么样的关系?2.解决数学问题的过程中你会注意哪些问题?体会到了哪些数学思想?学生活动学生畅所欲言,分享自己的收获与体验。设计意图:引导学生回顾勾股定理及其逆定理,明确其基本应用.引导学生回顾和体会解题的思路和数学思想方法.环节五:达标检测教师活动给出题目:一、选择题1.已知直角三角形两边的长分别为5、12,则第三边的长为( )A. 13 B. 60 C. 17 D. 13或2.下列条件中,不能判断△ABC为直角三角形的是( )A. a=1.5 b=2 c=2.5 B. a:b:c=5:12:13C. ∠A+∠B=∠C D. ∠A:∠B:∠C=3:4:5二、填空题3.写出定理“直角三角形斜边上的中线等于斜边的一半”的逆命题:___________.4.如图小方格都是边长为1的正方形,则四边形ABCD的面积是___________.学生活动独立完成设计意图:测试学生目标达成情况。
板书设计勾股定理及其逆定理例题解题思路。学生板演过程
作业与拓展学习设计必做题:教材38页第8,9,10题选做题:教材39页第14题。
特色学习资源分析、技术手段应用说明(结合教学特色和实际撰写)借助《几何画板》工具演示立体图形展开成平面图形过程中对应点的关系,帮助学生理解最短路径问题.PPT展示课件,方便大量例题与习题的呈现。希沃展台的使用更快地呈现许多学生练习过程。
教学反思与改进本节课要求学生能够将本章的知识内容形成体系,选择适当的定理,并结合分类讨论,方程思想等数学思想综合的解决问题,对学生的要求较高.学生可能在性质和判定的使用上存在障碍,不能够综合地分析问题,选择最优化的解决问题的途径.应对策略在教学中,应该注意强调勾股定理及其逆定理的作用的不同,理清解决几何问题和实际问题所需要的必备的条件中是需要直角还是已知直角求边长,从而综合并且熟练地使用勾股定理及其逆定理.
