2024-2025学年九年级数学上册图形的相似、解直角三角形专项训练卷(二)(含答案)
文档属性
| 名称 | 2024-2025学年九年级数学上册图形的相似、解直角三角形专项训练卷(二)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 828.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 00:00:00 | ||
图片预览


文档简介
图形的相似、解直角三角形专项训练卷(二)
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
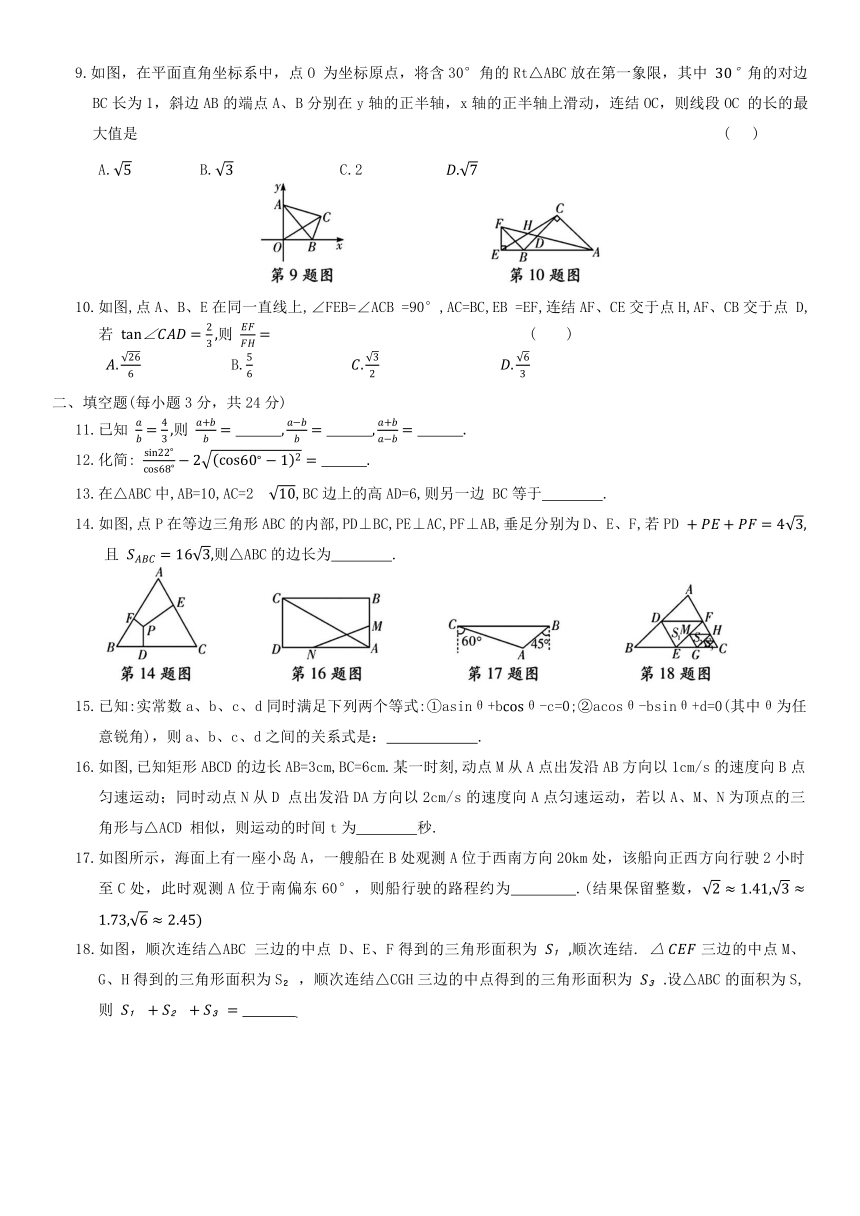
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠C=90°,则下列式子一定成立的是 ( )
A.= B. = C. = D.B
2.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AE:EC=5:3,BF=10,则CF的长为 ( )
A.16 B.8 C.4 D.6
3.如图,已知△ABC是正三角形,点D 是边 AC上一动点(不与A、C重合),以BD 为边作正△BDE,边DE 与边AB交于点 F,则图中一定相似的三角形有 ( )
A.6对 B.5对 C.4对 D.3对
4.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',则下列说法错误的是( )
A.△ABC∽△A'B'C' B. CO:CA'=1:2
C. A、O、A'三点在同一直线上 D. AC∥A'C'
5.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和10cm,另一个三角形的最短边长为2.5cm,则它的最长边为 ( )
A.3cm B.4cm C.4.5cm D.5cm
6.如图,一辆小车沿倾斜角为α的斜坡向上行驶13 m,已知 则小车上升的高度是 ( )
A. 5m B.6m C.6.5m D.7m
7.如图所示,在△ABC中,D为线段AB的中点,AE=3EC,延长DE交BC的延长线于F,则 为 ( )
A.2:1 B.3:1 C.3:2 D.4:3
8.在以O为坐标原点的平面直角坐标内,有一点A(3,4),射线OA与x轴正半轴的夹角为α,那么cosα的值为 ( )
A. B.
9.如图,在平面直角坐标系中,点O 为坐标原点,将含30°角的Rt△ABC放在第一象限,其中 角的对边BC长为1,斜边AB的端点A、B分别在y轴的正半轴,x轴的正半轴上滑动,连结OC,则线段OC 的长的最大值是 ( )
A. B. C.2
10.如图,点A、B、E在同一直线上,∠FEB=∠ACB =90°,AC=BC,EB =EF,连结AF、CE交于点H,AF、CB交于点 D,若 则 ( )
B.
二、填空题(每小题3分,共24分)
11.已知 则
12.化简:
13.在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边 BC等于 .
14.如图,点P在等边三角形ABC的内部,PD⊥BC,PE⊥AC,PF⊥AB,垂足分别为D、E、F,若PD 且 则△ABC的边长为 .
15.已知:实常数a、b、c、d同时满足下列两个等式:①+-c=0;②-+d=0(其中θ为任意锐角),则a、b、c、d之间的关系式是: .
16.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D 点出发沿DA方向以2cm/s的速度向A点匀速运动,若以A、M、N为顶点的三角形与△ACD 相似,则运动的时间t为 秒.
17.如图所示,海面上有一座小岛A,一艘船在B处观测A位于西南方向20km处,该船向正西方向行驶2小时至C处,此时观测A位于南偏东60°,则船行驶的路程约为 .(结果保留整数,
18.如图,顺次连结△ABC 三边的中点 D、E、F得到的三角形面积为 顺次连结. 三边的中点M、G、H得到的三角形面积为S ,顺次连结△CGH三边的中点得到的三角形面积为 设△ABC的面积为S,则
三、解答题(共66分)
19.(8分). 中,已知 试判断 的形状.
20.(10分)已知:如图. 三个顶点的坐标分别为 ,正方形网格中,每个小正方形的边长是1 个单位长度.
(1)画出 向上平移6个单位得到的
(2)以点C为位似中心,在网格中画出. 使 与 位似,且 与 的位似比为2:1,并直接写出点 的坐标.
21.(11分)如图,在平行四边形ABCD中,过点A 作. ,垂足为 E,连结DE,F为线段 DE上一点,且
(1)求证:
(2)若 求AF 的长.
22.(11分)如图,等边 的边长为12,D 为AB 边上一动点,过点 D 作 于点E.过点E作 于点 F.
(1)若 求AF的长.
(2)当AD取何值时,
23.(12分)如图, 是一块锐角三角形材料,高线AH长8cm,底边 BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点 D、G分别在AB、AC上,AH交DG于 M.
(1)求证:
(2)加工成的矩形零件 DEFG 的面积能否等于 若能,求出宽DE的长度;否则,请说明理由.
24.(14分)如图1为放置在水平桌面l上的台灯,底座的高AB 为5cm ,长度均为20cm 的连杆BC、CD与AB 始终在同一平面上.
(1)转动连杆BC,CD,使 成平角, ,如图2,求连杆端点 D 离桌面l的高度 DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当时台灯光线最佳.求此时连杆端点 D 离桌面l的高度比原来降低了多少厘米
图形的相似、解直角三角形专项训练卷(二)
1. D 2. D 3. B 4. B 5. D 6. A 7. A 8. A 9. C 10. A
11. 7 12.0 13.6或10 14.8
16.2.4或1.5 17.39 km 18.2
19.解:由题意,得
解得
∴∠A=∠B=∠C=60°.
∴ △ABC为等边三角形.
20.解:(1)如图所示:△A B C ,即为所求.
(2)如图所示:△A B C 即为所求,A 的坐标是(-2,-2).
21.(1)证明:∵ 四边形ABCD 是平行四边形,
∴AD∥BC,AB∥CD.
∴∠ADF=∠CED,∠B+∠C=180°.
∵ ∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,∴ △ADF∽△DEC.
(2)解:∵四边形ABCD 是平行四边形,
∴AD∥BC,CD=AB=4.
又∵AE⊥BC,∴EA⊥AD.
在Rt△ADE 中,
∵△ADF∽△DEC,
即
22.解:(1)∵AB=12,AD=2,
∴BD=AB-AD=10.
在Rt△BDE中,
在Rt△CFE中,
(2)在△BDE和△EFC中,
∴△BDE≌△CEF(AAS).
∴BE=CF.
∴BD=2BE=8.
∴AD=AB--BD=4.
即AD=4时,DE=EF.
23.(1)证明:∵ 四边形 DEFG为矩形,
∴DG∥EF.
∴△ADG∽△ABC.
(2)解:加工成的矩形零件 DEFG的面积不能等于 理由如下:
当加工成的矩形零件 DEFG的面积等于:时,设宽DE的长度为 xcm,
则
∵高线AH长8cm ,底边 BC长10 cm,
整理,得
∴x无实数根,
故加工成的矩形零件 DEFG的面积不能等于
24.解:(1)如图2,过B作. 于 O.
∴ 四边形ABOE 是矩形.
(2)如图3,过B作 于H,过C作( 于G,CK 于K,
由题意,得.
在 中,
在 中,
答:比原来降低了(
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1.在Rt△ABC中,∠C=90°,则下列式子一定成立的是 ( )
A.= B. = C. = D.B
2.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AE:EC=5:3,BF=10,则CF的长为 ( )
A.16 B.8 C.4 D.6
3.如图,已知△ABC是正三角形,点D 是边 AC上一动点(不与A、C重合),以BD 为边作正△BDE,边DE 与边AB交于点 F,则图中一定相似的三角形有 ( )
A.6对 B.5对 C.4对 D.3对
4.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',则下列说法错误的是( )
A.△ABC∽△A'B'C' B. CO:CA'=1:2
C. A、O、A'三点在同一直线上 D. AC∥A'C'
5.要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为5cm,6cm和10cm,另一个三角形的最短边长为2.5cm,则它的最长边为 ( )
A.3cm B.4cm C.4.5cm D.5cm
6.如图,一辆小车沿倾斜角为α的斜坡向上行驶13 m,已知 则小车上升的高度是 ( )
A. 5m B.6m C.6.5m D.7m
7.如图所示,在△ABC中,D为线段AB的中点,AE=3EC,延长DE交BC的延长线于F,则 为 ( )
A.2:1 B.3:1 C.3:2 D.4:3
8.在以O为坐标原点的平面直角坐标内,有一点A(3,4),射线OA与x轴正半轴的夹角为α,那么cosα的值为 ( )
A. B.
9.如图,在平面直角坐标系中,点O 为坐标原点,将含30°角的Rt△ABC放在第一象限,其中 角的对边BC长为1,斜边AB的端点A、B分别在y轴的正半轴,x轴的正半轴上滑动,连结OC,则线段OC 的长的最大值是 ( )
A. B. C.2
10.如图,点A、B、E在同一直线上,∠FEB=∠ACB =90°,AC=BC,EB =EF,连结AF、CE交于点H,AF、CB交于点 D,若 则 ( )
B.
二、填空题(每小题3分,共24分)
11.已知 则
12.化简:
13.在△ABC中,AB=10,AC=2 ,BC边上的高AD=6,则另一边 BC等于 .
14.如图,点P在等边三角形ABC的内部,PD⊥BC,PE⊥AC,PF⊥AB,垂足分别为D、E、F,若PD 且 则△ABC的边长为 .
15.已知:实常数a、b、c、d同时满足下列两个等式:①+-c=0;②-+d=0(其中θ为任意锐角),则a、b、c、d之间的关系式是: .
16.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动;同时动点N从D 点出发沿DA方向以2cm/s的速度向A点匀速运动,若以A、M、N为顶点的三角形与△ACD 相似,则运动的时间t为 秒.
17.如图所示,海面上有一座小岛A,一艘船在B处观测A位于西南方向20km处,该船向正西方向行驶2小时至C处,此时观测A位于南偏东60°,则船行驶的路程约为 .(结果保留整数,
18.如图,顺次连结△ABC 三边的中点 D、E、F得到的三角形面积为 顺次连结. 三边的中点M、G、H得到的三角形面积为S ,顺次连结△CGH三边的中点得到的三角形面积为 设△ABC的面积为S,则
三、解答题(共66分)
19.(8分). 中,已知 试判断 的形状.
20.(10分)已知:如图. 三个顶点的坐标分别为 ,正方形网格中,每个小正方形的边长是1 个单位长度.
(1)画出 向上平移6个单位得到的
(2)以点C为位似中心,在网格中画出. 使 与 位似,且 与 的位似比为2:1,并直接写出点 的坐标.
21.(11分)如图,在平行四边形ABCD中,过点A 作. ,垂足为 E,连结DE,F为线段 DE上一点,且
(1)求证:
(2)若 求AF 的长.
22.(11分)如图,等边 的边长为12,D 为AB 边上一动点,过点 D 作 于点E.过点E作 于点 F.
(1)若 求AF的长.
(2)当AD取何值时,
23.(12分)如图, 是一块锐角三角形材料,高线AH长8cm,底边 BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点 D、G分别在AB、AC上,AH交DG于 M.
(1)求证:
(2)加工成的矩形零件 DEFG 的面积能否等于 若能,求出宽DE的长度;否则,请说明理由.
24.(14分)如图1为放置在水平桌面l上的台灯,底座的高AB 为5cm ,长度均为20cm 的连杆BC、CD与AB 始终在同一平面上.
(1)转动连杆BC,CD,使 成平角, ,如图2,求连杆端点 D 离桌面l的高度 DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当时台灯光线最佳.求此时连杆端点 D 离桌面l的高度比原来降低了多少厘米
图形的相似、解直角三角形专项训练卷(二)
1. D 2. D 3. B 4. B 5. D 6. A 7. A 8. A 9. C 10. A
11. 7 12.0 13.6或10 14.8
16.2.4或1.5 17.39 km 18.2
19.解:由题意,得
解得
∴∠A=∠B=∠C=60°.
∴ △ABC为等边三角形.
20.解:(1)如图所示:△A B C ,即为所求.
(2)如图所示:△A B C 即为所求,A 的坐标是(-2,-2).
21.(1)证明:∵ 四边形ABCD 是平行四边形,
∴AD∥BC,AB∥CD.
∴∠ADF=∠CED,∠B+∠C=180°.
∵ ∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,∴ △ADF∽△DEC.
(2)解:∵四边形ABCD 是平行四边形,
∴AD∥BC,CD=AB=4.
又∵AE⊥BC,∴EA⊥AD.
在Rt△ADE 中,
∵△ADF∽△DEC,
即
22.解:(1)∵AB=12,AD=2,
∴BD=AB-AD=10.
在Rt△BDE中,
在Rt△CFE中,
(2)在△BDE和△EFC中,
∴△BDE≌△CEF(AAS).
∴BE=CF.
∴BD=2BE=8.
∴AD=AB--BD=4.
即AD=4时,DE=EF.
23.(1)证明:∵ 四边形 DEFG为矩形,
∴DG∥EF.
∴△ADG∽△ABC.
(2)解:加工成的矩形零件 DEFG的面积不能等于 理由如下:
当加工成的矩形零件 DEFG的面积等于:时,设宽DE的长度为 xcm,
则
∵高线AH长8cm ,底边 BC长10 cm,
整理,得
∴x无实数根,
故加工成的矩形零件 DEFG的面积不能等于
24.解:(1)如图2,过B作. 于 O.
∴ 四边形ABOE 是矩形.
(2)如图3,过B作 于H,过C作( 于G,CK 于K,
由题意,得.
在 中,
在 中,
答:比原来降低了(
