18.1平行四边形的性质与判定 作业设计 人教版数学八年级下册
文档属性
| 名称 | 18.1平行四边形的性质与判定 作业设计 人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 156.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 00:00:00 | ||
图片预览


文档简介
《平行四边形的性质与判定》作业设计
一、作业设计目标
1.通过思考与推理运算,建构平行四边形的性质和判定的知识网络。加深对平行四边形的性质和判定方法的理解。
2.综合运用平行四边形的判定和性质解决问题,加强对“数形结合”、“分类讨论”、“化归”等数学思想与方法的体会,提 升推理能力、逻辑思维能力和直观想象能力。
3.经历数学问题的剖析、思维过程及实际问题的解决,感受数学的实际应用价值和应用数学的意识,提高运用数学知识解决实际问题的能力,提升数学核心素养。
重难点:
通过思考与推理运算,建构平行四边形的性质和判定的知识网络。加深对平行四边形的性质和判定方法的理解。
二、作业实施过程与策略
学生独立完成,教师面批,共分为三部分作业,学生根据自身有选择的完成作业,教师不对学生进行主观上的分层。
(一)基础巩固性作业
1.(教材P43练习)在口ABCD中,AD=3cm,AB=2cm,则口ABCD的周长为 .
2.在口ABCD中,
(1)若∠A=125°,则∠B= °,∠C= °,∠D= °.
(2)若∠A+∠C=140°,则∠A= °∠B= °
3.(教材P44练习 )如图,口ABCD的对角线ACBD相交于点0,且AD=8,BD=12,AC=6,则△OBC的周长为
4.已知:四边形ABCD,从下列条件中任取两个条件加以组合,能判定四边形ABCD是平行四边形的组合是
①AB//CD ②BC//AD ③AB=CD④BC=AD⑤∠A=∠C⑥∠B=∠D⑦A0=0C;⑧DO=BO;
5.(教材第47页例4)如图,在口ABCD中,EF分别为AB、CD上两点,
1)若AE=CE连接DEBE四边形DEBI为平行四边形吗 你能用不同方法说明吗
2)若DE、B分别是∠ADC和∠ABC的角平分线,交AB、CD于点EF四边形BEDF还是平行四边形吗 说明理由。
[设计意图]第123题分别从边、角、对角线考查对平行四边形性质的理解,第4题考查对平行四边形判定的理解,第5题是对平行四边形性质与判定的综合应用。以题代知识点,通过对教材的例题和习题的变式与改编,以问题串形式回顾平行四边形的概念、性质和判定等知识,让学生通过推理、计算等过程,进一步完善知识体系,尝试构建思维导图。通过问题串,反馈学生对平行四边形的性质和判定的理解和简单应用。
(二)能力提升性作业
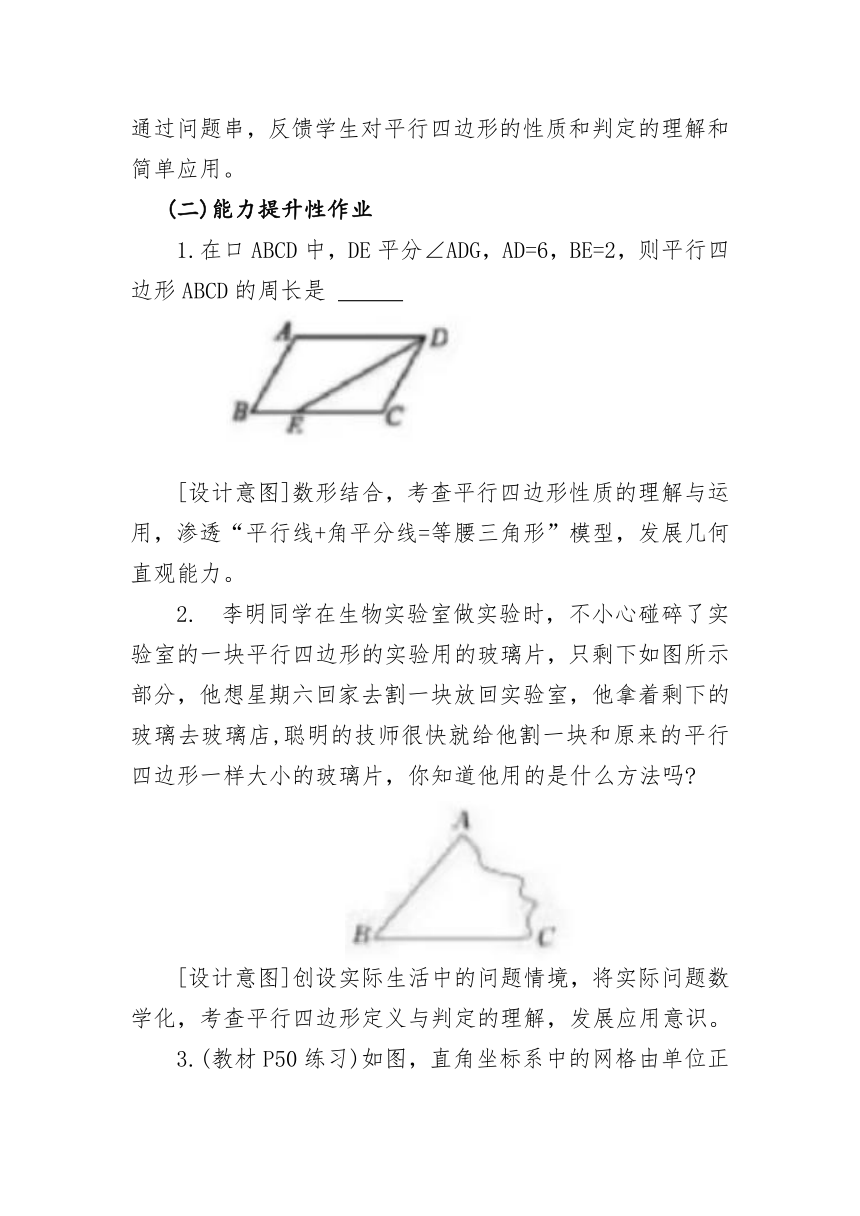
1.在口ABCD中,DE平分∠ADG,AD=6,BE=2,则平行四边形ABCD的周长是
[设计意图]数形结合,考查平行四边形性质的理解与运用,渗透“平行线+角平分线=等腰三角形”模型,发展几何直观能力。
李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想星期六回家去割一块放回实验室,他拿着剩下的玻璃去玻璃店,聪明的技师很快就给他割一块和原来的平行四边形一样大小的玻璃片,你知道他用的是什么方法吗
[设计意图]创设实际生活中的问题情境,将实际问题数学化,考查平行四边形定义与判定的理解,发展应用意识。
3.(教材P50练习)如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3),B点坐标为(- 2,0),C点坐标为(0,-1),若以A、B、C及点D为顶点的四边形为平行四边形ABCD 在图中画出平行四边形ABCD并写出D点的坐标
[设计意图]通过对教材习题的变式,体会数形结合、分类讨论的思想方法。总结平行四边形存在性问题的通性通法,理解这一类数学问题的解决方法,提升直观想象等数学核心素养。
4.(教材第46页例3)如图,在口ABCD中,EF是线段AC上的两点,且有AE=CF,
①四边形BFDE是平行四边形吗 为什么
②当点EF在直线AC上时四边形BFDE还是平行四边形吗 为什么
③若AF=CE结论是否仍然成立 请说明理由.④若BEIIDF结论是否仍然成立 请说明理由
BE⊥AC于E, DF⊥AC于F,结论是否仍然成立 请说明理由.
[设计意图](用不同方法解决)考查证明平行四边形的方法的确定及平行四边形的判定定理的应用,通过条件的变化,体会判定方法的灵活运用及解决问题策略的多样性,及不同方法之间的比较,体会到证明方法的优化选择。发展推理能力、逻辑思维能力。
(三)拓展拔高性作业
1.(教材P51练习)从前,一位农场主有一大块田地。其形状是一个平行四边形(图中的口ABCD)田地内有一口井。位于图中的点P处井所占的面积非常有限,与整片田地比起来简直可以看成“一点”(面积可忽略不计),现在农场主要把这块田平均分给两个儿子,且使两块地共用这口水井,请你利用所学数学知识进行设计,并说明你的理由
[设计意图]利用平行四边形性质解决面积相等问题,把知识融入到实际问题的故事情境中,让学生感受到数学知识来源于生活,又服务于生活.体会数学知识的应用价值,发展应用意识。
2.以“思维导图”,“手抄报”或“数学日记”等形式对本节知识内容进行梳理:总结求解平行四边形问题常用的数学思想方法;回顾平行四边形的研究要素、研究思路、研究方法是什么 归纳几何图形研究的一般思路和方法。
三、作业设计效果反思
本节是在学行四边形的定义、性质、判定后设计的,旨在复习巩固平行四边形的定义、性质、判定,达到理解与应用的目的:作业设计有层次梯度性,通过层层递进习题,使不同层次学生都能得到提高,人人都能获得必需的数学,不同的人在数学上得到不同的发展,基础巩固类作业适用于全体学生,能力提升类适用于中等偏上学生,拔高拓展类适用于学优生;学生根据自身学习力有选择的完成作业,教师不对学生进行主观上的分层,以保护学生的自尊心。学优生在巩固基础知识的同时不断拓展,提高了数学思维能力和综合运用能力,学困生不因解决不了难题而抄袭作业,学生更感兴趣,乐于完成。基于“双减”的数学课,重在提升学生的能力,发展学生的核心素养,本设计注重对学生基础知识与基本能力的考查,通过对问题的解决,总结求解平行四边形问题常用的数学思想方法以及几何图形研究的一般思路和方法,为后续学习特殊平行四边形做基础:加深学生对数学学科思想方法(“数形结合”、“分类讨论”、“化归”等)和关键能力(推理能力、逻辑思维能力和直观想象能力,应用意识)的培养。
一、作业设计目标
1.通过思考与推理运算,建构平行四边形的性质和判定的知识网络。加深对平行四边形的性质和判定方法的理解。
2.综合运用平行四边形的判定和性质解决问题,加强对“数形结合”、“分类讨论”、“化归”等数学思想与方法的体会,提 升推理能力、逻辑思维能力和直观想象能力。
3.经历数学问题的剖析、思维过程及实际问题的解决,感受数学的实际应用价值和应用数学的意识,提高运用数学知识解决实际问题的能力,提升数学核心素养。
重难点:
通过思考与推理运算,建构平行四边形的性质和判定的知识网络。加深对平行四边形的性质和判定方法的理解。
二、作业实施过程与策略
学生独立完成,教师面批,共分为三部分作业,学生根据自身有选择的完成作业,教师不对学生进行主观上的分层。
(一)基础巩固性作业
1.(教材P43练习)在口ABCD中,AD=3cm,AB=2cm,则口ABCD的周长为 .
2.在口ABCD中,
(1)若∠A=125°,则∠B= °,∠C= °,∠D= °.
(2)若∠A+∠C=140°,则∠A= °∠B= °
3.(教材P44练习 )如图,口ABCD的对角线ACBD相交于点0,且AD=8,BD=12,AC=6,则△OBC的周长为
4.已知:四边形ABCD,从下列条件中任取两个条件加以组合,能判定四边形ABCD是平行四边形的组合是
①AB//CD ②BC//AD ③AB=CD④BC=AD⑤∠A=∠C⑥∠B=∠D⑦A0=0C;⑧DO=BO;
5.(教材第47页例4)如图,在口ABCD中,EF分别为AB、CD上两点,
1)若AE=CE连接DEBE四边形DEBI为平行四边形吗 你能用不同方法说明吗
2)若DE、B分别是∠ADC和∠ABC的角平分线,交AB、CD于点EF四边形BEDF还是平行四边形吗 说明理由。
[设计意图]第123题分别从边、角、对角线考查对平行四边形性质的理解,第4题考查对平行四边形判定的理解,第5题是对平行四边形性质与判定的综合应用。以题代知识点,通过对教材的例题和习题的变式与改编,以问题串形式回顾平行四边形的概念、性质和判定等知识,让学生通过推理、计算等过程,进一步完善知识体系,尝试构建思维导图。通过问题串,反馈学生对平行四边形的性质和判定的理解和简单应用。
(二)能力提升性作业
1.在口ABCD中,DE平分∠ADG,AD=6,BE=2,则平行四边形ABCD的周长是
[设计意图]数形结合,考查平行四边形性质的理解与运用,渗透“平行线+角平分线=等腰三角形”模型,发展几何直观能力。
李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想星期六回家去割一块放回实验室,他拿着剩下的玻璃去玻璃店,聪明的技师很快就给他割一块和原来的平行四边形一样大小的玻璃片,你知道他用的是什么方法吗
[设计意图]创设实际生活中的问题情境,将实际问题数学化,考查平行四边形定义与判定的理解,发展应用意识。
3.(教材P50练习)如图,直角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3),B点坐标为(- 2,0),C点坐标为(0,-1),若以A、B、C及点D为顶点的四边形为平行四边形ABCD 在图中画出平行四边形ABCD并写出D点的坐标
[设计意图]通过对教材习题的变式,体会数形结合、分类讨论的思想方法。总结平行四边形存在性问题的通性通法,理解这一类数学问题的解决方法,提升直观想象等数学核心素养。
4.(教材第46页例3)如图,在口ABCD中,EF是线段AC上的两点,且有AE=CF,
①四边形BFDE是平行四边形吗 为什么
②当点EF在直线AC上时四边形BFDE还是平行四边形吗 为什么
③若AF=CE结论是否仍然成立 请说明理由.④若BEIIDF结论是否仍然成立 请说明理由
BE⊥AC于E, DF⊥AC于F,结论是否仍然成立 请说明理由.
[设计意图](用不同方法解决)考查证明平行四边形的方法的确定及平行四边形的判定定理的应用,通过条件的变化,体会判定方法的灵活运用及解决问题策略的多样性,及不同方法之间的比较,体会到证明方法的优化选择。发展推理能力、逻辑思维能力。
(三)拓展拔高性作业
1.(教材P51练习)从前,一位农场主有一大块田地。其形状是一个平行四边形(图中的口ABCD)田地内有一口井。位于图中的点P处井所占的面积非常有限,与整片田地比起来简直可以看成“一点”(面积可忽略不计),现在农场主要把这块田平均分给两个儿子,且使两块地共用这口水井,请你利用所学数学知识进行设计,并说明你的理由
[设计意图]利用平行四边形性质解决面积相等问题,把知识融入到实际问题的故事情境中,让学生感受到数学知识来源于生活,又服务于生活.体会数学知识的应用价值,发展应用意识。
2.以“思维导图”,“手抄报”或“数学日记”等形式对本节知识内容进行梳理:总结求解平行四边形问题常用的数学思想方法;回顾平行四边形的研究要素、研究思路、研究方法是什么 归纳几何图形研究的一般思路和方法。
三、作业设计效果反思
本节是在学行四边形的定义、性质、判定后设计的,旨在复习巩固平行四边形的定义、性质、判定,达到理解与应用的目的:作业设计有层次梯度性,通过层层递进习题,使不同层次学生都能得到提高,人人都能获得必需的数学,不同的人在数学上得到不同的发展,基础巩固类作业适用于全体学生,能力提升类适用于中等偏上学生,拔高拓展类适用于学优生;学生根据自身学习力有选择的完成作业,教师不对学生进行主观上的分层,以保护学生的自尊心。学优生在巩固基础知识的同时不断拓展,提高了数学思维能力和综合运用能力,学困生不因解决不了难题而抄袭作业,学生更感兴趣,乐于完成。基于“双减”的数学课,重在提升学生的能力,发展学生的核心素养,本设计注重对学生基础知识与基本能力的考查,通过对问题的解决,总结求解平行四边形问题常用的数学思想方法以及几何图形研究的一般思路和方法,为后续学习特殊平行四边形做基础:加深学生对数学学科思想方法(“数形结合”、“分类讨论”、“化归”等)和关键能力(推理能力、逻辑思维能力和直观想象能力,应用意识)的培养。
