河南模式2024-2025学年八年级上学期期末数学试卷四(含解析)
文档属性
| 名称 | 河南模式2024-2025学年八年级上学期期末数学试卷四(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-10 00:00:00 | ||
图片预览


文档简介
河南模式2024-2025学年八年级上学期期末数学试卷(四)
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.秋天到了,同学们收集了很多漂亮的落叶,下面的落叶中,不是轴对称图形的是( )
A. B. C. D.
2.“燕山雪花大如席,片片吹落轩辕台.”这是唐代诗人李白的《北风行》中的诗句.据测定,5000~10000片雪花约有1克,一般新雪的密度为每立方厘米0.05克~0.1克,这说明一片雪花是非常轻的.数据“0.05克”用科学记数法表示为( )
A.千克 B.千克 C.千克 D.千克
3.下列计算正确的是( )
A. B. C. D.
4.已知,下面是“作一个角等于已知角,即作”的尺规作图痕迹.该尺规作图的依据是( )
A. B. C. D.
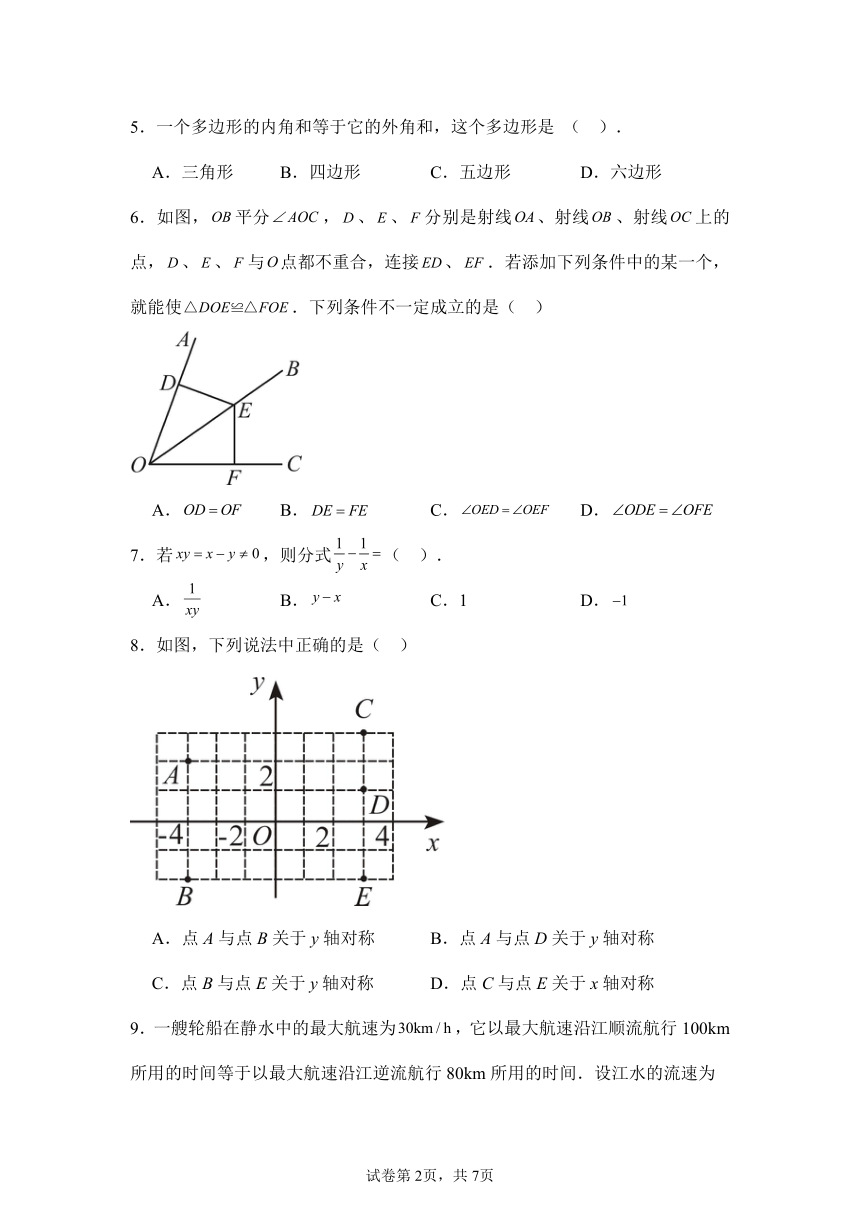
5.一个多边形的内角和等于它的外角和,这个多边形是 ( ).
A.三角形 B.四边形 C.五边形 D.六边形
6.如图,平分,、、分别是射线、射线、射线上的点,、、与点都不重合,连接、.若添加下列条件中的某一个,就能使.下列条件不一定成立的是( )
A. B. C. D.
7.若,则分式( ).
A. B. C.1 D.
8.如图,下列说法中正确的是( )
A.点A与点B关于y轴对称 B.点A与点D关于y轴对称
C.点B与点E关于y轴对称 D.点C与点E关于x轴对称
9.一艘轮船在静水中的最大航速为,它以最大航速沿江顺流航行100km所用的时间等于以最大航速沿江逆流航行80km所用的时间.设江水的流速为,则可列方程为( )
A. B. C. D.
10.如图,已知,点D、E分别在、上且,连接交于点M,连接,过点A分别作,垂足分别为F、G,下列结论:①;②;③平分;④如果,则E是的中点;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题)
二、填空题
11.若代数式有意义,则实数的取值范围是 .
12.分解因式:3ax2+6axy+3ay2= .
13.在中,,则边上的中线的取值范围是 .
14.两个边长分别为和的正方形如图1放置,其未重叠部分(阴影)面积为,若再在图1中大正方形的右下角摆放一个边长为的小正方形(如图2),两个小正方形重叠部分(阴影)面积为,则可用含,的代数式表示为 .
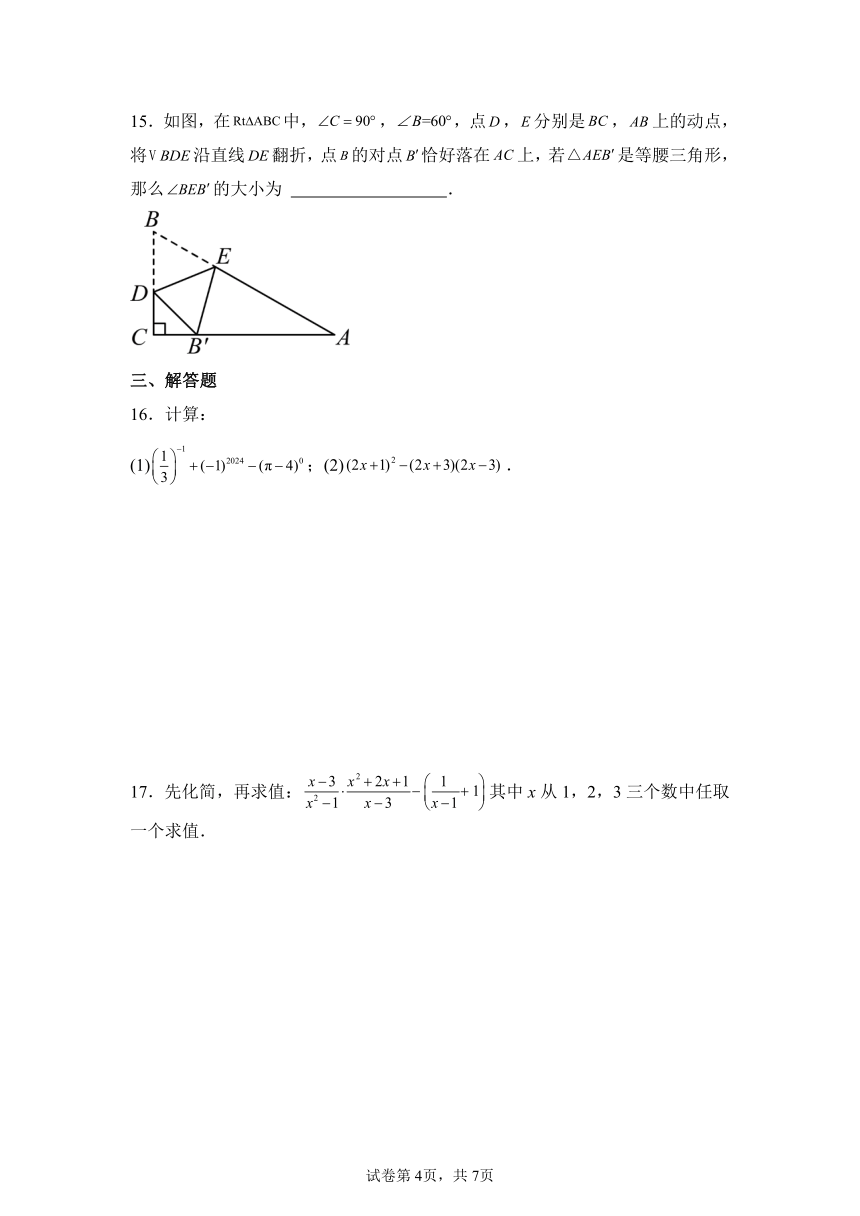
15.如图,在中,,,点,分别是,上的动点,将沿直线翻折,点的对点恰好落在上,若是等腰三角形,那么的大小为 .
三、解答题
16.计算:
(1);(2).
17.先化简,再求值:其中x从1,2,3三个数中任取一个求值.
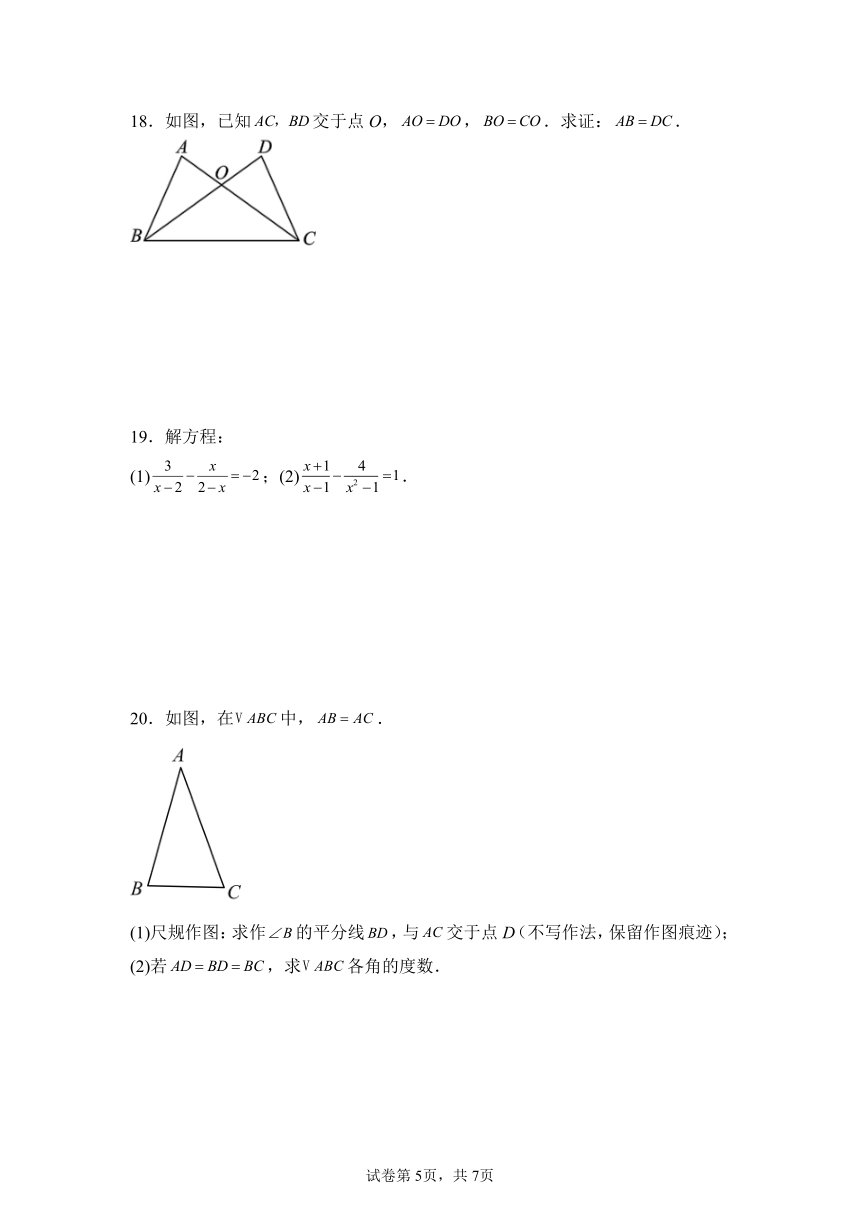
18.如图,已知交于点O,,.求证:.
19.解方程:
(1);(2).
20.如图,在中,.
(1)尺规作图:求作的平分线,与交于点D(不写作法,保留作图痕迹);
(2)若,求各角的度数.
21.阅读理解:将代数式转化为的形式(其中m、k为常数),则,其中.
(1)仿照此法将代数式化为的形式,并指出m、k的值;
(2)已知在初中数学学习中,一个数的平方总是非负数,请问有最小值或者最大值吗?有的话,请说明是最小值还是最大值,并求出这个值,以及此时x的取值.
22.如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A出发以1cm/s的速度向点C运动,同时点E从点C出发以2cm/s的速度向点B运动,运动的时间为t秒,解决以下问题:
(1)当t为何值时,△DEC为等边三角形;
(2)当t为何值时,△DEC为直角三角形.
23.(1)如图①,中,,平分,交于E,于D,与交于点F,.线段和的数量关系是 .
(2)如图②,中,,平分,,垂足E在的延长线上.试探究线段和的数量关系,并证明你的结论.
(3)如图③,中,,点D在线段上,,,垂足为E,与相交于点F.试探究线段与的数量关系,并证明你的结论.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D B B B C C C D
1.D
【分析】本题主要考查了轴对称图形的识别,解题的关键在于能够熟练掌握轴对称图形的定义.根据轴对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就叫做对称轴.
【详解】解:A、B、C中的图形是轴对称图形,故A、B、C不符合题意,
D、图形不是轴对称图形,故D符合题意.
故选:D.
2.D
【分析】本题主要考查科学记数法.科学记数法的表示形式为的形式,其中,n为整数.解题关键是正确确定a的值以及n的值.
科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正整数;当原数的绝对值时,n是负整数.
【详解】解:0.05克千克千克.
故选:D.
3.D
【分析】本题考查幂的运算.根据幂的运算法则,逐一计算后,判断即可.掌握相关运算法则,是解题的关键.
【详解】解:A、,选项错误;
B、,选项错误;
C、,选项错误;
D、,选项正确;
故选D.
4.B
【分析】本题主要考查了尺规作图作一个角等于已知角、全等三角形的判定等知识点,掌握尺规作图作一个角等于已知角的作法成为解题的关键.根据“作一个角等于已知角,即作”的尺规作图痕迹,结合全等三角形的判定定理即可解答.
【详解】解:由题意可知,“作一个角等于已知角,即作”的尺规作图的依据是.
故选:B.
5.B
【分析】本题主要考查的是多边形的内角和与外角和,掌握n边形的内角和为、外角和是是解题的关键.
根据多边形的内角和的计算公式与外角和是列出方程,解方程即可.
【详解】解:设这个多边形边数是n,根据题意得:
,
解得:,
∴这个多边形是四边形.
故选:B.
6.B
【分析】
由平分,得,由公共边,然后根据全等三角形的判定定理可得答案.
【详解】
解:平分,
,
又,
∴若添加,根据“”可得;故A选项不符合题意;
若添加,根据“”可得;故C选项不符合题意;
若添加,根据“”可得;故D选项不符合题意;
故选B.
【点睛】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
7.C
【分析】此题应先将分式通分,然后由已知xy=x y≠0,即可得出原分式的值.
【详解】解:原分式,
∵xy=x y≠0,
∴=1.
故答案为:C.
【点睛】本题主要考查分式的化简求值,解题的关键是将原分式进行准确的通分.
8.C
【分析】根据各个点的坐标及两点关于坐标轴对称的点的特征即可完成.
【详解】A、点A( 3,2)与点B( 3,-2)关于x轴对称,故说法错误;
B、点A( 3,2)与点D(3,1)不关于y轴对称,故说法错误;
C、点B( 3,-2) 与点E(3,-2)关于y轴对称,故说法正确;
D、点C(3,3) 与点E(3,-2)不关于x轴对称,故说法错误;
故选:C
【点睛】本题考查了确定点的坐标及两点关于坐标轴对称,掌握两点关于坐标轴对称是关键.
9.C
【解析】略
10.D
【分析】根据三角形全等的判定定理和性质,角平分线的性质定理的逆定理,三角形的面积公式,四边形的内角和定理,补角的定义等逐一判断即可.
【详解】∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE,BE=CD,
∴∠EBM=∠DCM,
∵∠BME=∠CMD,
∴△BME≌△CMD,
∴结论①正确;
∵,
∴∠FAG+∠FMG=180°,
∵∠EMB+∠FMG=180°,
∴∠FAG=∠EMB,
∴结论②正确;
∵△BME≌△CMD,
∴∠BEM=∠CDM,
∴∠AEF=∠ADG,
∵,AE=AD,
∴△AEF≌△ADG,
∴AF=AG,
∴MA平分∠EMD,
∴结论③正确;
∵△BME≌△CMD,
∴∠BEM=∠CDM,EM=DM,
∴∠AEM=∠ADM,
∵AE=AD,
∴△AEM≌△ADM,
∴,
∵,
∴,
∴E是AB的中点,
∴结论④正确;
故选D.
【点睛】本题考查了全等三角形的判定和性质,角的平分线的性质定理的逆定理,邻角,四边形的内角和定理,三角形的面积,熟练掌握三角形全等的判定和性质是解题的关键.
11.
【分析】本题主要考查了分式有意义的条件,掌握分式有意义的条件为分母不等于零是解题的关键
直接运用分式有意义的条件列不等式求解即可.
【详解】解:∵数式有意义,
∴,即.
故答案为.
12.3a(x+y)2.
【分析】先提取公因式3a,再对余下的多项式利用完全平方公式继续分解.
【详解】解:3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2.
故答案为3a(x+y)2.
【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
13.
【分析】本题考查了全等三角形的判定与性质,三角形三边的不等关系;延长至E,使,连接,证明,再由三角形三边不等关系即可求解.倍长中线是关键.
【详解】解:延长至E,使,连接.
在和中,
,
∴,
∴.
在中,,
即,
故.
故答案为:.
14.
【分析】本题主要考查乘法公式与几何图形的结合,体现了数形结合的思想.分别用含a,b的式子表示,,即可得到答案.
【详解】解:如图1,;
图2:;
∴ ,
故答案为:.
15.或或
【分析】本题考查直角三角形中的折叠问题,三角形内角和定理,等腰三角形的性质,解题的关键是掌握等腰三角形性质,分类讨论.
由,,得,分三种情况讨论:①当时,可得;②当时,即得,即得;③当时,可得.
【详解】解:,,
,
分三种情况讨论:
①当时,如图:
,
;
②当时,如图:
,
;
③当时,如图:
,
;
综上所述,为或或,
故答案为:或或.
16.(1)
(2)
【分析】本题考查实数的混合运算,整式的混合运算,熟练掌握运算法则是解此题的关键.
(1)先计算零指数幂,乘方运算,负整数指数幂的计算,再进行加减运算即可;
(2)先计算完全平方公式和平方差公式,再合并同类项即可.
【详解】(1)解:原式
;
(2)原式
.
17.,时,原式
【分析】本题考查分式的化简求值,根据分式的混合运算法则,进行化简,再选择一个使分式有意义的值,代入求值即可.掌握分式的混合运算法则,正确的计算,是解题的关键.
【详解】解:原式
;
要使原式有意义,则,
所以x的值只能取2,
当时,原式.
18.见解析
【分析】由,,,根据证明,即可得到结论.
【详解】证明:在和中,
,
∴,
∴.
【点睛】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定是解题的关键.
19.(1);
(2)原方程无解.
【分析】()方程先变形,再去分母,去括号,移项,合并同类项,系数化为,检验,即可求出解;
()先对方程的分母因式分解,再去分母,去括号,移项,合并同类项,系数化为,检验,即可求出解;
本题考查了解分式方程,熟练掌握分式方程的解法是解题的关键.
【详解】(1)解:方程变形得,,
方程两边同时乘以最简公分母得,,
去括号得,,
移项得,,
合并同类项得,,
系数化为得,,
检验:把代入最简公分母得,,
∴原方程的解是;
(2)解:方程变形得,,
方程两边同时乘以最简公分母得,
,
去括号得,,
移项得,,
合并同类项得,,
系数化为得,,
检验:把代入最简公分母得,,
∴原方程无解.
20.(1)见解析
(2)
【分析】本题考查尺规作图—作角平分线,等边对等角,三角形的内角和定理.
(1)根据尺规作角平分线的方法,作图即可;
(2)设,利用等边对等角以及三角形的内角和定理,进行求解即可.
【详解】(1)解:如图所示,即为所求;
(2)设,
,
,
,
又,
,
又,
,
在中,由三角形内角和定理得:
,
即,
解得,
,
.
21.(1);
(2)有最大值,最大值为,此时
【分析】(1)根据示例给出的方法将代数式转化为的形式即可,
(2)将代数式转化为的形式,然后根据平方的非负性求解即可.
【详解】(1)仿照示例的方法可得:
∴.
(2)
∵
∴
∴
∴当时,有最大值.
【点睛】本题考查完全平方公式的变形,熟练掌握完全平方公式的形式是解决本题的关键.
22.(1)当t为2时,△DEC为等边三角形;(2)当t为 或3时,△DEC为直角三角形.
【分析】(1)根据等边三角形的性质列出方程求出t的值;
(2)分两种情况讨论:①当∠DEC为直角时,②当∠EDC为直角时,分别利用30度角所对的直角边等于斜边的一半列方程求出t的值.
【详解】(1)根据题意可得 AD=t,CD=6﹣t,CE=2t,
∵∠B=30°,AC=6cm,
∴BC=2AC=12cm,
∵∠C=90°﹣∠B=30°=60°,△DEC为等边三角形,
∴CD=CE,
6﹣t=2t,
t=2,
∴当t为2时,△DEC为等边三角形;
(2)①当∠DEC为直角时,∠EDC=30°,
∴CE=,
2t=(6﹣t),
t=;
②当∠EDC为直角时,∠DEC=30°,
CD=CE,
6﹣t= 2t,
t=3.
∴当t为或3时,△DEC为直角三角形.
【点睛】本题考查了等边三角形的性质,含30度角的直角三角形的性质,熟练掌握30度角的直角三角形的边角关系是解题的关键.
23.(1);(2).理由见解析;(3).理由见解析
【分析】(1)利用等腰三角形三线合一的性质得出,,然后利用证明,得出,即可得出结论;
(2)延长,交于点G,证明,得出,利用余角的性质证明,根据等腰三角形的判定得出,然后利用等腰三角形三线合一的性质即可得出结论;
(3)过点D作交于H,交的延长线于点G,先证明是等腰直角三角形,得出,进而得出,利用等腰三角形的判定可得出,然后类似(2)判定即可.
【详解】解:(1),平分,
,,
又,
,
在在和中
,
,
.
故答案为:;
(2).理由如下:
如图②,延长,交于点G,
,
,
又,
,
,
.
在和中
,
.
又CD平分,
,
由得
,
,
是BG的中点,
,
.
(3).理由如下:
过点D作交于H,交的延长线于点G,
则,
,
是等腰直角三角形,
,
又,
.
又,
∴由(2)可知,
,
,
,
即平分,
∴由(2)可知,
是的中点,
,
.
【点睛】本题考查了等腰三角形与全等三角形的判定与性质,解题的关键是熟练的掌握等腰三角形与全等三角形的判定与性质.
试卷第1页,共3页
试卷第1页,共3页
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.秋天到了,同学们收集了很多漂亮的落叶,下面的落叶中,不是轴对称图形的是( )
A. B. C. D.
2.“燕山雪花大如席,片片吹落轩辕台.”这是唐代诗人李白的《北风行》中的诗句.据测定,5000~10000片雪花约有1克,一般新雪的密度为每立方厘米0.05克~0.1克,这说明一片雪花是非常轻的.数据“0.05克”用科学记数法表示为( )
A.千克 B.千克 C.千克 D.千克
3.下列计算正确的是( )
A. B. C. D.
4.已知,下面是“作一个角等于已知角,即作”的尺规作图痕迹.该尺规作图的依据是( )
A. B. C. D.
5.一个多边形的内角和等于它的外角和,这个多边形是 ( ).
A.三角形 B.四边形 C.五边形 D.六边形
6.如图,平分,、、分别是射线、射线、射线上的点,、、与点都不重合,连接、.若添加下列条件中的某一个,就能使.下列条件不一定成立的是( )
A. B. C. D.
7.若,则分式( ).
A. B. C.1 D.
8.如图,下列说法中正确的是( )
A.点A与点B关于y轴对称 B.点A与点D关于y轴对称
C.点B与点E关于y轴对称 D.点C与点E关于x轴对称
9.一艘轮船在静水中的最大航速为,它以最大航速沿江顺流航行100km所用的时间等于以最大航速沿江逆流航行80km所用的时间.设江水的流速为,则可列方程为( )
A. B. C. D.
10.如图,已知,点D、E分别在、上且,连接交于点M,连接,过点A分别作,垂足分别为F、G,下列结论:①;②;③平分;④如果,则E是的中点;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
第II卷(非选择题)
二、填空题
11.若代数式有意义,则实数的取值范围是 .
12.分解因式:3ax2+6axy+3ay2= .
13.在中,,则边上的中线的取值范围是 .
14.两个边长分别为和的正方形如图1放置,其未重叠部分(阴影)面积为,若再在图1中大正方形的右下角摆放一个边长为的小正方形(如图2),两个小正方形重叠部分(阴影)面积为,则可用含,的代数式表示为 .
15.如图,在中,,,点,分别是,上的动点,将沿直线翻折,点的对点恰好落在上,若是等腰三角形,那么的大小为 .
三、解答题
16.计算:
(1);(2).
17.先化简,再求值:其中x从1,2,3三个数中任取一个求值.
18.如图,已知交于点O,,.求证:.
19.解方程:
(1);(2).
20.如图,在中,.
(1)尺规作图:求作的平分线,与交于点D(不写作法,保留作图痕迹);
(2)若,求各角的度数.
21.阅读理解:将代数式转化为的形式(其中m、k为常数),则,其中.
(1)仿照此法将代数式化为的形式,并指出m、k的值;
(2)已知在初中数学学习中,一个数的平方总是非负数,请问有最小值或者最大值吗?有的话,请说明是最小值还是最大值,并求出这个值,以及此时x的取值.
22.如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A出发以1cm/s的速度向点C运动,同时点E从点C出发以2cm/s的速度向点B运动,运动的时间为t秒,解决以下问题:
(1)当t为何值时,△DEC为等边三角形;
(2)当t为何值时,△DEC为直角三角形.
23.(1)如图①,中,,平分,交于E,于D,与交于点F,.线段和的数量关系是 .
(2)如图②,中,,平分,,垂足E在的延长线上.试探究线段和的数量关系,并证明你的结论.
(3)如图③,中,,点D在线段上,,,垂足为E,与相交于点F.试探究线段与的数量关系,并证明你的结论.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D B B B C C C D
1.D
【分析】本题主要考查了轴对称图形的识别,解题的关键在于能够熟练掌握轴对称图形的定义.根据轴对称图形的定义进行逐一判断即可:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就叫做对称轴.
【详解】解:A、B、C中的图形是轴对称图形,故A、B、C不符合题意,
D、图形不是轴对称图形,故D符合题意.
故选:D.
2.D
【分析】本题主要考查科学记数法.科学记数法的表示形式为的形式,其中,n为整数.解题关键是正确确定a的值以及n的值.
科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正整数;当原数的绝对值时,n是负整数.
【详解】解:0.05克千克千克.
故选:D.
3.D
【分析】本题考查幂的运算.根据幂的运算法则,逐一计算后,判断即可.掌握相关运算法则,是解题的关键.
【详解】解:A、,选项错误;
B、,选项错误;
C、,选项错误;
D、,选项正确;
故选D.
4.B
【分析】本题主要考查了尺规作图作一个角等于已知角、全等三角形的判定等知识点,掌握尺规作图作一个角等于已知角的作法成为解题的关键.根据“作一个角等于已知角,即作”的尺规作图痕迹,结合全等三角形的判定定理即可解答.
【详解】解:由题意可知,“作一个角等于已知角,即作”的尺规作图的依据是.
故选:B.
5.B
【分析】本题主要考查的是多边形的内角和与外角和,掌握n边形的内角和为、外角和是是解题的关键.
根据多边形的内角和的计算公式与外角和是列出方程,解方程即可.
【详解】解:设这个多边形边数是n,根据题意得:
,
解得:,
∴这个多边形是四边形.
故选:B.
6.B
【分析】
由平分,得,由公共边,然后根据全等三角形的判定定理可得答案.
【详解】
解:平分,
,
又,
∴若添加,根据“”可得;故A选项不符合题意;
若添加,根据“”可得;故C选项不符合题意;
若添加,根据“”可得;故D选项不符合题意;
故选B.
【点睛】本题主要考查全等三角形的判定,熟练掌握全等三角形的判定定理是解题的关键.
7.C
【分析】此题应先将分式通分,然后由已知xy=x y≠0,即可得出原分式的值.
【详解】解:原分式,
∵xy=x y≠0,
∴=1.
故答案为:C.
【点睛】本题主要考查分式的化简求值,解题的关键是将原分式进行准确的通分.
8.C
【分析】根据各个点的坐标及两点关于坐标轴对称的点的特征即可完成.
【详解】A、点A( 3,2)与点B( 3,-2)关于x轴对称,故说法错误;
B、点A( 3,2)与点D(3,1)不关于y轴对称,故说法错误;
C、点B( 3,-2) 与点E(3,-2)关于y轴对称,故说法正确;
D、点C(3,3) 与点E(3,-2)不关于x轴对称,故说法错误;
故选:C
【点睛】本题考查了确定点的坐标及两点关于坐标轴对称,掌握两点关于坐标轴对称是关键.
9.C
【解析】略
10.D
【分析】根据三角形全等的判定定理和性质,角平分线的性质定理的逆定理,三角形的面积公式,四边形的内角和定理,补角的定义等逐一判断即可.
【详解】∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE,BE=CD,
∴∠EBM=∠DCM,
∵∠BME=∠CMD,
∴△BME≌△CMD,
∴结论①正确;
∵,
∴∠FAG+∠FMG=180°,
∵∠EMB+∠FMG=180°,
∴∠FAG=∠EMB,
∴结论②正确;
∵△BME≌△CMD,
∴∠BEM=∠CDM,
∴∠AEF=∠ADG,
∵,AE=AD,
∴△AEF≌△ADG,
∴AF=AG,
∴MA平分∠EMD,
∴结论③正确;
∵△BME≌△CMD,
∴∠BEM=∠CDM,EM=DM,
∴∠AEM=∠ADM,
∵AE=AD,
∴△AEM≌△ADM,
∴,
∵,
∴,
∴E是AB的中点,
∴结论④正确;
故选D.
【点睛】本题考查了全等三角形的判定和性质,角的平分线的性质定理的逆定理,邻角,四边形的内角和定理,三角形的面积,熟练掌握三角形全等的判定和性质是解题的关键.
11.
【分析】本题主要考查了分式有意义的条件,掌握分式有意义的条件为分母不等于零是解题的关键
直接运用分式有意义的条件列不等式求解即可.
【详解】解:∵数式有意义,
∴,即.
故答案为.
12.3a(x+y)2.
【分析】先提取公因式3a,再对余下的多项式利用完全平方公式继续分解.
【详解】解:3ax2+6axy+3ay2
=3a(x2+2xy+y2)
=3a(x+y)2.
故答案为3a(x+y)2.
【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
13.
【分析】本题考查了全等三角形的判定与性质,三角形三边的不等关系;延长至E,使,连接,证明,再由三角形三边不等关系即可求解.倍长中线是关键.
【详解】解:延长至E,使,连接.
在和中,
,
∴,
∴.
在中,,
即,
故.
故答案为:.
14.
【分析】本题主要考查乘法公式与几何图形的结合,体现了数形结合的思想.分别用含a,b的式子表示,,即可得到答案.
【详解】解:如图1,;
图2:;
∴ ,
故答案为:.
15.或或
【分析】本题考查直角三角形中的折叠问题,三角形内角和定理,等腰三角形的性质,解题的关键是掌握等腰三角形性质,分类讨论.
由,,得,分三种情况讨论:①当时,可得;②当时,即得,即得;③当时,可得.
【详解】解:,,
,
分三种情况讨论:
①当时,如图:
,
;
②当时,如图:
,
;
③当时,如图:
,
;
综上所述,为或或,
故答案为:或或.
16.(1)
(2)
【分析】本题考查实数的混合运算,整式的混合运算,熟练掌握运算法则是解此题的关键.
(1)先计算零指数幂,乘方运算,负整数指数幂的计算,再进行加减运算即可;
(2)先计算完全平方公式和平方差公式,再合并同类项即可.
【详解】(1)解:原式
;
(2)原式
.
17.,时,原式
【分析】本题考查分式的化简求值,根据分式的混合运算法则,进行化简,再选择一个使分式有意义的值,代入求值即可.掌握分式的混合运算法则,正确的计算,是解题的关键.
【详解】解:原式
;
要使原式有意义,则,
所以x的值只能取2,
当时,原式.
18.见解析
【分析】由,,,根据证明,即可得到结论.
【详解】证明:在和中,
,
∴,
∴.
【点睛】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定是解题的关键.
19.(1);
(2)原方程无解.
【分析】()方程先变形,再去分母,去括号,移项,合并同类项,系数化为,检验,即可求出解;
()先对方程的分母因式分解,再去分母,去括号,移项,合并同类项,系数化为,检验,即可求出解;
本题考查了解分式方程,熟练掌握分式方程的解法是解题的关键.
【详解】(1)解:方程变形得,,
方程两边同时乘以最简公分母得,,
去括号得,,
移项得,,
合并同类项得,,
系数化为得,,
检验:把代入最简公分母得,,
∴原方程的解是;
(2)解:方程变形得,,
方程两边同时乘以最简公分母得,
,
去括号得,,
移项得,,
合并同类项得,,
系数化为得,,
检验:把代入最简公分母得,,
∴原方程无解.
20.(1)见解析
(2)
【分析】本题考查尺规作图—作角平分线,等边对等角,三角形的内角和定理.
(1)根据尺规作角平分线的方法,作图即可;
(2)设,利用等边对等角以及三角形的内角和定理,进行求解即可.
【详解】(1)解:如图所示,即为所求;
(2)设,
,
,
,
又,
,
又,
,
在中,由三角形内角和定理得:
,
即,
解得,
,
.
21.(1);
(2)有最大值,最大值为,此时
【分析】(1)根据示例给出的方法将代数式转化为的形式即可,
(2)将代数式转化为的形式,然后根据平方的非负性求解即可.
【详解】(1)仿照示例的方法可得:
∴.
(2)
∵
∴
∴
∴当时,有最大值.
【点睛】本题考查完全平方公式的变形,熟练掌握完全平方公式的形式是解决本题的关键.
22.(1)当t为2时,△DEC为等边三角形;(2)当t为 或3时,△DEC为直角三角形.
【分析】(1)根据等边三角形的性质列出方程求出t的值;
(2)分两种情况讨论:①当∠DEC为直角时,②当∠EDC为直角时,分别利用30度角所对的直角边等于斜边的一半列方程求出t的值.
【详解】(1)根据题意可得 AD=t,CD=6﹣t,CE=2t,
∵∠B=30°,AC=6cm,
∴BC=2AC=12cm,
∵∠C=90°﹣∠B=30°=60°,△DEC为等边三角形,
∴CD=CE,
6﹣t=2t,
t=2,
∴当t为2时,△DEC为等边三角形;
(2)①当∠DEC为直角时,∠EDC=30°,
∴CE=,
2t=(6﹣t),
t=;
②当∠EDC为直角时,∠DEC=30°,
CD=CE,
6﹣t= 2t,
t=3.
∴当t为或3时,△DEC为直角三角形.
【点睛】本题考查了等边三角形的性质,含30度角的直角三角形的性质,熟练掌握30度角的直角三角形的边角关系是解题的关键.
23.(1);(2).理由见解析;(3).理由见解析
【分析】(1)利用等腰三角形三线合一的性质得出,,然后利用证明,得出,即可得出结论;
(2)延长,交于点G,证明,得出,利用余角的性质证明,根据等腰三角形的判定得出,然后利用等腰三角形三线合一的性质即可得出结论;
(3)过点D作交于H,交的延长线于点G,先证明是等腰直角三角形,得出,进而得出,利用等腰三角形的判定可得出,然后类似(2)判定即可.
【详解】解:(1),平分,
,,
又,
,
在在和中
,
,
.
故答案为:;
(2).理由如下:
如图②,延长,交于点G,
,
,
又,
,
,
.
在和中
,
.
又CD平分,
,
由得
,
,
是BG的中点,
,
.
(3).理由如下:
过点D作交于H,交的延长线于点G,
则,
,
是等腰直角三角形,
,
又,
.
又,
∴由(2)可知,
,
,
,
即平分,
∴由(2)可知,
是的中点,
,
.
【点睛】本题考查了等腰三角形与全等三角形的判定与性质,解题的关键是熟练的掌握等腰三角形与全等三角形的判定与性质.
试卷第1页,共3页
试卷第1页,共3页
同课章节目录
