期末巩固训练2024-2025学年 人教版数学九年级上册(含答案)
文档属性
| 名称 | 期末巩固训练2024-2025学年 人教版数学九年级上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 383.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 20:53:09 | ||
图片预览


文档简介
期末巩固训练2024-2025学年 人教版数学九年级上册
一、单选题(共10题;共30分)
1.(3分)不透明袋子中装有9个球,其中有7个绿球、2个白球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是白球的概率是( )
A. B. C. D.
2.(3分)如图,圆心重合的两圆半径分别为4、2,,则阴影部分图形的面积为( )
A.4π B. C.8π D.16π
3.(3分)一元二次方程 的两根为 , 则 的值为 ( )
A. B.-3 C.3 D.
4.(3分)如图,已知平面直角坐标系中的,点,,坐标系内存在直线l:将分成面积相等的两部分,且这条直线与两坐标轴围成的三角形的面积为1,则的值为( )
A.4或 B.0或 C.0或 D.4或
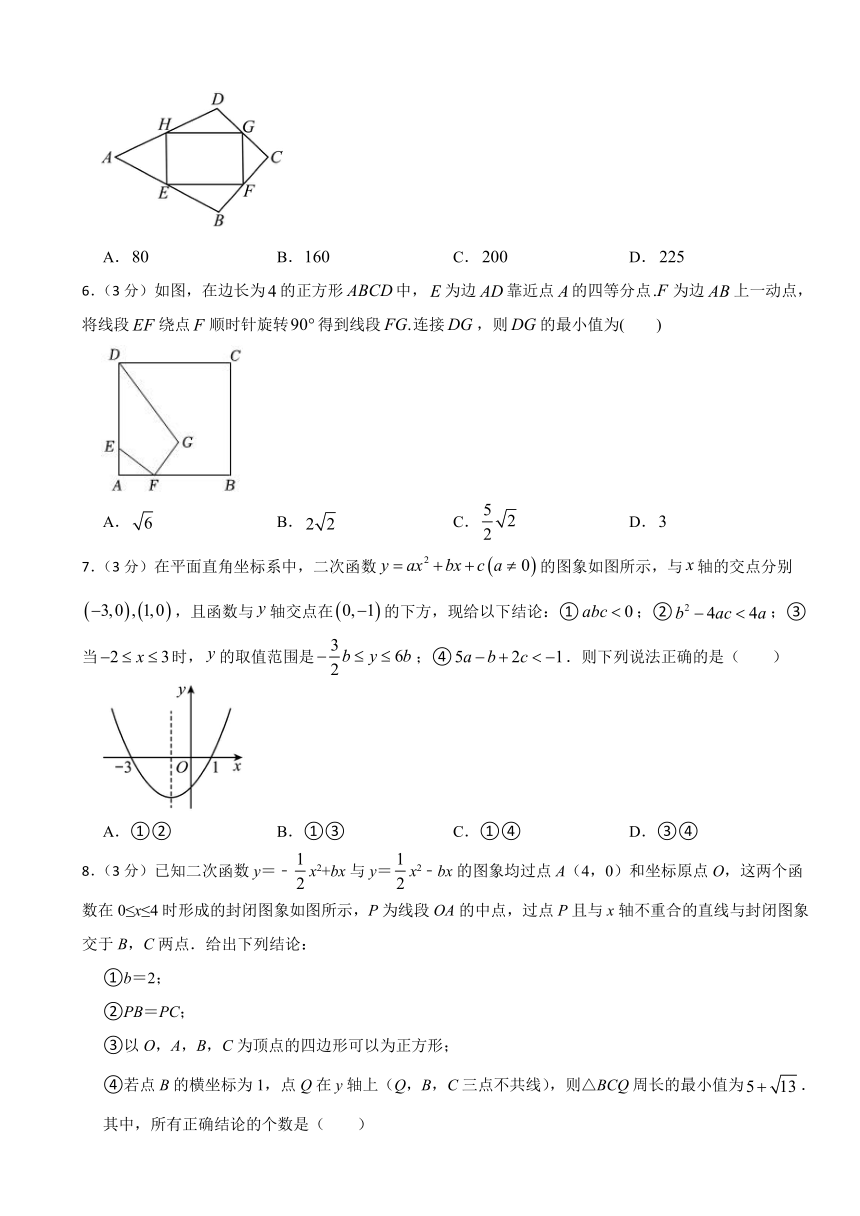
5.(3分)如图,在四边形中,点,,,分别是四边的中点,若四边形是矩形,且其周长是,则四边形的面积的最大值是( )
A. B. C. D.
6.(3分)如图,在边长为的正方形中,为边靠近点的四等分点为边上一动点,将线段绕点顺时针旋转得到线段连接,则的最小值为( )
A. B. C. D.
7.(3分)在平面直角坐标系中,二次函数的图象如图所示,与轴的交点分别,且函数与轴交点在的下方,现给以下结论:①;②;③当时,的取值范围是;④.则下列说法正确的是( )
A.①② B.①③ C.①④ D.③④
8.(3分)已知二次函数y=﹣x2+bx与y=x2﹣bx的图象均过点A(4,0)和坐标原点O,这两个函数在0≤x≤4时形成的封闭图象如图所示,P为线段OA的中点,过点P且与x轴不重合的直线与封闭图象交于B,C两点.给出下列结论:
①b=2;
②PB=PC;
③以O,A,B,C为顶点的四边形可以为正方形;
④若点B的横坐标为1,点Q在y轴上(Q,B,C三点不共线),则△BCQ周长的最小值为.
其中,所有正确结论的个数是( )
A.1 B.2 C.3 D.4
9.(3分)如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
10.(3分)已知二次函数下列结论正确的是( )
①已知点,点在二次函数的图象上,则;②该图象一定过定点和;③直线与抛物线一定存在两个交点;④当时,的最小值是,则.
A.①②③ B.①③④ C.②③④ D.①②③④
二、填空题(共7题;共21分)
11.(3分)如图,在中,,,,点是线段上的一个动点,连接,将线段绕点逆时针旋转得到线段,连接,则线段的最小值是 .
12.(3分)把抛物线向右平移3个单位,再向上平移1个单位,所得抛物线的解析式为 .
13.(3分)在一个不透明的布袋中装有红色、蓝色、白色玻璃球共60个,除颜色外其他安全相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在0.15左右,则口袋中红色球可能有 个.
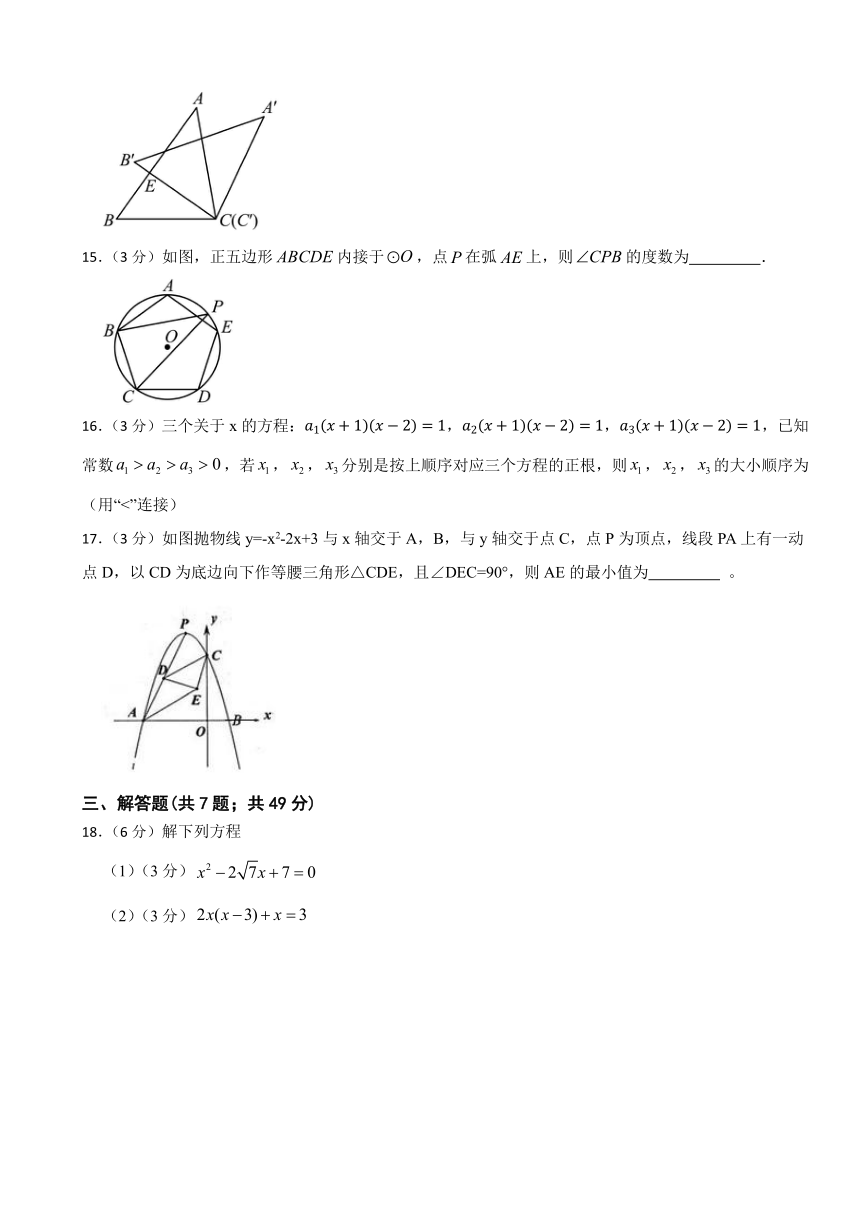
14.(3分)如图,把绕点C按顺时针方向旋转后能与重合,且交于点E,若,则的度数是 .
15.(3分)如图,正五边形内接于,点在弧上,则的度数为 .
16.(3分)三个关于x的方程:,,,已知常数,若,,分别是按上顺序对应三个方程的正根,则,,的大小顺序为 (用“<”连接)
17.(3分)如图抛物线y=-x2-2x+3与x轴交于A,B,与y轴交于点C,点P为顶点,线段PA上有一动点D,以CD为底边向下作等腰三角形△CDE,且∠DEC=90°,则AE的最小值为 。
三、解答题(共7题;共49分)
18.(6分)解下列方程
(1)(3分)
(2)(3分)
19.(6分)酚酞试液是化学实验室中一种常见的酸碱指示剂,广泛应用于酸碱滴定过程中,通常情况下,酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.一次化学实验课上,老师让学生用酚酞溶液检测4瓶因标签污损无法分辨的无色溶液的酸碱性,已知这4种溶液分别是:盐酸(呈酸性)、硝酸钾溶液(呈中性)、氢氧化钠溶液(呈碱性)、氢氧化钙溶液(呈碱性)中的一种.
(1)(3分)小明将酚酞试液随机滴入其中1瓶溶液里,结果变红的概率是多少?
(2)(3分)小明和小亮从中各选1瓶溶液滴入酚酞试液进行检测,请你用列表或画树状图的方法,求2瓶溶液中1瓶变红、1瓶不变色的概率.
20.(6分)如图,已知抛物线经过,两点.
(1)(3分)求抛物线的函数表达式和顶点坐标;
(2)(3分)当时,求y的取值范围.
21.(7分)在一次游艺活动中,组织者设计了一个抛硬币游戏,玩这个游戏需要4张票,每张票0.5元.一个游戏者抛两枚硬币,如果硬币落地后都是正面朝上,则游戏者得到一件奖品,奖品价值5元.组织者能指望从这个游戏中盈利吗?为什么?
22.(7分)已知关于x 的一元二次方程有两个相等的实数根,求m的值.
23.(8分)已知关于的方程.
(1)(2分)若是方程的解,求的值;
(2)(3分)若原方程有实数根,求的取值范围;
(3)(3分)若方程的两根分别为,且,求的值.
24.(9分)已知抛物线经过,两点.
(1)(4分)求抛物线所对应的函数表达式;
(2)(5分)直线l:(k、t是常数,)与抛物线有且只有一个公共点.
①求直线l所对应的函数表达式;
②将直线l向下平移2个单位得到直线,过点A的直线m:与抛物线的另一个交点为D(异于点B),过点B的直线n:与抛物线的另一交点为E(异于点A),当直线m,n的交点P在定直线上时,试探究直线是否过定点?若过定点,求出该定点的坐标:若不过定点,请说明理由.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】A
11.【答案】
12.【答案】
13.【答案】9
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】(1)
(2),
19.【答案】(1)
(2)
20.【答案】(1)抛物线解析式为,顶点坐标为
(2)
21.【答案】解: ∵游戏者抛两枚硬币, 硬币落地后朝上一面的可能性共有以下4种等可能的结果数:正正,正反,反正,反反,其中两枚硬币落地后都是正面朝上的情况数只有1种,
∴ P( 都正面朝上的可能性 )=,
∴ 组织者收入4×0.5×4=8(元),
而一人获奖,支出5元,8>5
∴组织者能盈利.
22.【答案】解:由可得:
方程有两个相等的实数根,
所以的值为2.
23.【答案】(1)
(2)
(3)m的值不存在
24.【答案】(1)
(2)①;②直线过定点
一、单选题(共10题;共30分)
1.(3分)不透明袋子中装有9个球,其中有7个绿球、2个白球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是白球的概率是( )
A. B. C. D.
2.(3分)如图,圆心重合的两圆半径分别为4、2,,则阴影部分图形的面积为( )
A.4π B. C.8π D.16π
3.(3分)一元二次方程 的两根为 , 则 的值为 ( )
A. B.-3 C.3 D.
4.(3分)如图,已知平面直角坐标系中的,点,,坐标系内存在直线l:将分成面积相等的两部分,且这条直线与两坐标轴围成的三角形的面积为1,则的值为( )
A.4或 B.0或 C.0或 D.4或
5.(3分)如图,在四边形中,点,,,分别是四边的中点,若四边形是矩形,且其周长是,则四边形的面积的最大值是( )
A. B. C. D.
6.(3分)如图,在边长为的正方形中,为边靠近点的四等分点为边上一动点,将线段绕点顺时针旋转得到线段连接,则的最小值为( )
A. B. C. D.
7.(3分)在平面直角坐标系中,二次函数的图象如图所示,与轴的交点分别,且函数与轴交点在的下方,现给以下结论:①;②;③当时,的取值范围是;④.则下列说法正确的是( )
A.①② B.①③ C.①④ D.③④
8.(3分)已知二次函数y=﹣x2+bx与y=x2﹣bx的图象均过点A(4,0)和坐标原点O,这两个函数在0≤x≤4时形成的封闭图象如图所示,P为线段OA的中点,过点P且与x轴不重合的直线与封闭图象交于B,C两点.给出下列结论:
①b=2;
②PB=PC;
③以O,A,B,C为顶点的四边形可以为正方形;
④若点B的横坐标为1,点Q在y轴上(Q,B,C三点不共线),则△BCQ周长的最小值为.
其中,所有正确结论的个数是( )
A.1 B.2 C.3 D.4
9.(3分)如图,菱形ABCD中的边长为1,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转30°得到菱形AB′CD′,B′C′交CD于点E,连接AE,CC′,则下列结论:①ΔAB′E≌ΔADE;②EC=ED;③AE⊥CC′;④四边形AB′ED的周长为 +2.其中符合题意结论的个数是( )
A.1 B.2 C.3 D.4
10.(3分)已知二次函数下列结论正确的是( )
①已知点,点在二次函数的图象上,则;②该图象一定过定点和;③直线与抛物线一定存在两个交点;④当时,的最小值是,则.
A.①②③ B.①③④ C.②③④ D.①②③④
二、填空题(共7题;共21分)
11.(3分)如图,在中,,,,点是线段上的一个动点,连接,将线段绕点逆时针旋转得到线段,连接,则线段的最小值是 .
12.(3分)把抛物线向右平移3个单位,再向上平移1个单位,所得抛物线的解析式为 .
13.(3分)在一个不透明的布袋中装有红色、蓝色、白色玻璃球共60个,除颜色外其他安全相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在0.15左右,则口袋中红色球可能有 个.
14.(3分)如图,把绕点C按顺时针方向旋转后能与重合,且交于点E,若,则的度数是 .
15.(3分)如图,正五边形内接于,点在弧上,则的度数为 .
16.(3分)三个关于x的方程:,,,已知常数,若,,分别是按上顺序对应三个方程的正根,则,,的大小顺序为 (用“<”连接)
17.(3分)如图抛物线y=-x2-2x+3与x轴交于A,B,与y轴交于点C,点P为顶点,线段PA上有一动点D,以CD为底边向下作等腰三角形△CDE,且∠DEC=90°,则AE的最小值为 。
三、解答题(共7题;共49分)
18.(6分)解下列方程
(1)(3分)
(2)(3分)
19.(6分)酚酞试液是化学实验室中一种常见的酸碱指示剂,广泛应用于酸碱滴定过程中,通常情况下,酚酞遇酸性和中性溶液不变色,遇碱性溶液变红色.一次化学实验课上,老师让学生用酚酞溶液检测4瓶因标签污损无法分辨的无色溶液的酸碱性,已知这4种溶液分别是:盐酸(呈酸性)、硝酸钾溶液(呈中性)、氢氧化钠溶液(呈碱性)、氢氧化钙溶液(呈碱性)中的一种.
(1)(3分)小明将酚酞试液随机滴入其中1瓶溶液里,结果变红的概率是多少?
(2)(3分)小明和小亮从中各选1瓶溶液滴入酚酞试液进行检测,请你用列表或画树状图的方法,求2瓶溶液中1瓶变红、1瓶不变色的概率.
20.(6分)如图,已知抛物线经过,两点.
(1)(3分)求抛物线的函数表达式和顶点坐标;
(2)(3分)当时,求y的取值范围.
21.(7分)在一次游艺活动中,组织者设计了一个抛硬币游戏,玩这个游戏需要4张票,每张票0.5元.一个游戏者抛两枚硬币,如果硬币落地后都是正面朝上,则游戏者得到一件奖品,奖品价值5元.组织者能指望从这个游戏中盈利吗?为什么?
22.(7分)已知关于x 的一元二次方程有两个相等的实数根,求m的值.
23.(8分)已知关于的方程.
(1)(2分)若是方程的解,求的值;
(2)(3分)若原方程有实数根,求的取值范围;
(3)(3分)若方程的两根分别为,且,求的值.
24.(9分)已知抛物线经过,两点.
(1)(4分)求抛物线所对应的函数表达式;
(2)(5分)直线l:(k、t是常数,)与抛物线有且只有一个公共点.
①求直线l所对应的函数表达式;
②将直线l向下平移2个单位得到直线,过点A的直线m:与抛物线的另一个交点为D(异于点B),过点B的直线n:与抛物线的另一交点为E(异于点A),当直线m,n的交点P在定直线上时,试探究直线是否过定点?若过定点,求出该定点的坐标:若不过定点,请说明理由.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】A
11.【答案】
12.【答案】
13.【答案】9
14.【答案】
15.【答案】
16.【答案】
17.【答案】
18.【答案】(1)
(2),
19.【答案】(1)
(2)
20.【答案】(1)抛物线解析式为,顶点坐标为
(2)
21.【答案】解: ∵游戏者抛两枚硬币, 硬币落地后朝上一面的可能性共有以下4种等可能的结果数:正正,正反,反正,反反,其中两枚硬币落地后都是正面朝上的情况数只有1种,
∴ P( 都正面朝上的可能性 )=,
∴ 组织者收入4×0.5×4=8(元),
而一人获奖,支出5元,8>5
∴组织者能盈利.
22.【答案】解:由可得:
方程有两个相等的实数根,
所以的值为2.
23.【答案】(1)
(2)
(3)m的值不存在
24.【答案】(1)
(2)①;②直线过定点
同课章节目录
