1.1 全等三角形 课件(共30张PPT) 2024-2025学年青岛版数学八年级上册
文档属性
| 名称 | 1.1 全等三角形 课件(共30张PPT) 2024-2025学年青岛版数学八年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 13:39:21 | ||
图片预览




文档简介
(共30张PPT)
第1章 全等三角形
1.1 全等三角形
这些是我们熟悉的图形,它们有什么特点?
同一张底片洗出
的同规格照片.
两张纸重合后的剪纸;
还有……?
举例
比一比:
裁下的纸板和
样板的形状、
大小是否 完
全 一样?能
完全重合吗?
思考
(7)
(6)
(3)
(1)
(2)
(4)
(5)
(8)
(9)
(10)
(11)
(12)
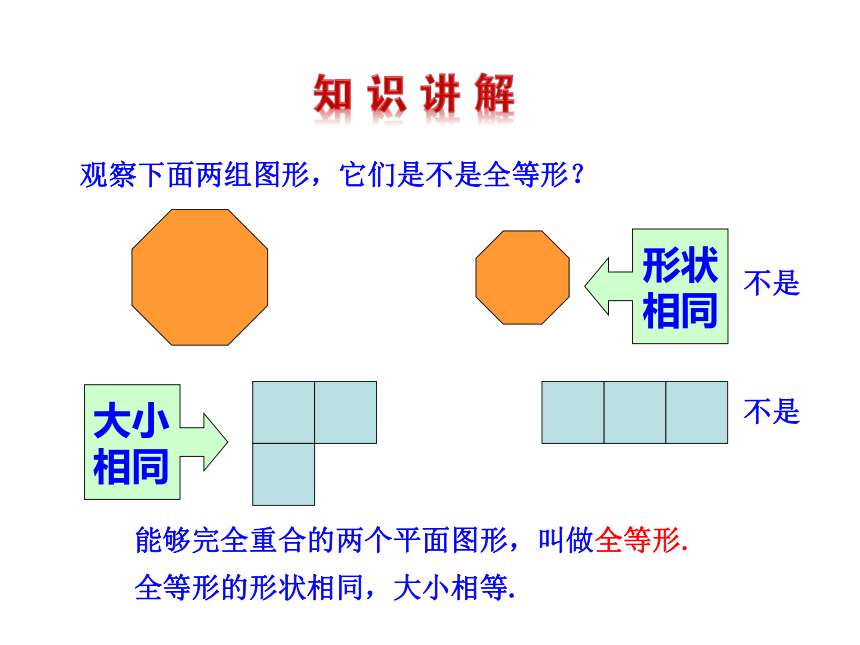
这些图形中有些是完全一样的,如果把它们叠在一起,它
们就能重合. 你能从图中找出这样的图形吗?
1.理解全等形的概念和特征.
2.能识别图形的全等,并能设计简单的图形.
3.掌握全等三角形的对应边相等、对应角相等.
4.能利用全等三角形的对应边相等、对应角相等进行简
单的推理和计算,解决一些实际问题.
全等形的形状相同,大小相等.
大小
相同
观察下面两组图形,它们是不是全等形?
形状
相同
不是
不是
能够完全重合的两个平面图形,叫做全等形.
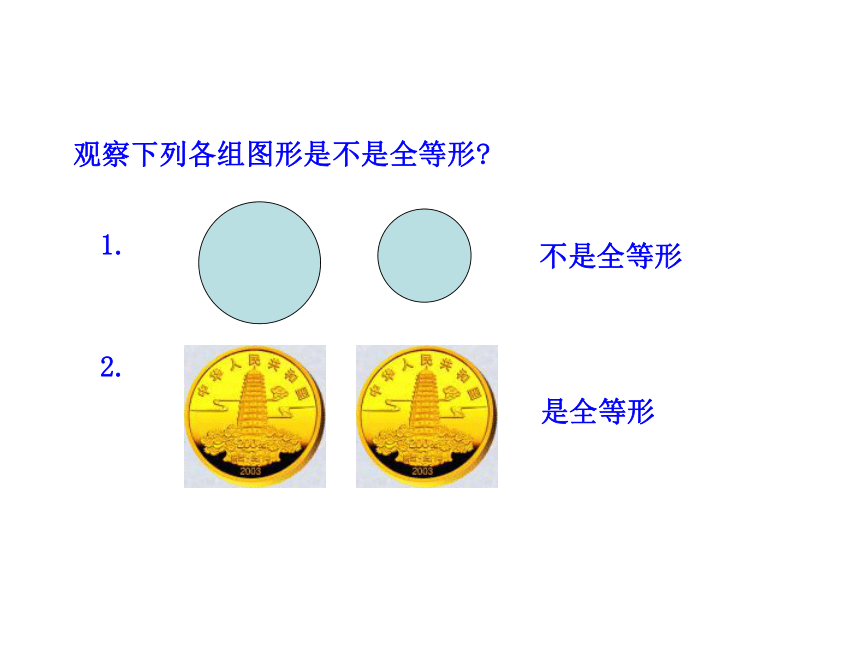
观察下列各组图形是不是全等形
1.
2.
不是全等形
是全等形
(1)
(2)
(3)
(4)
(5)
(10)
(7)
(8)
(9)
(14)
(15)
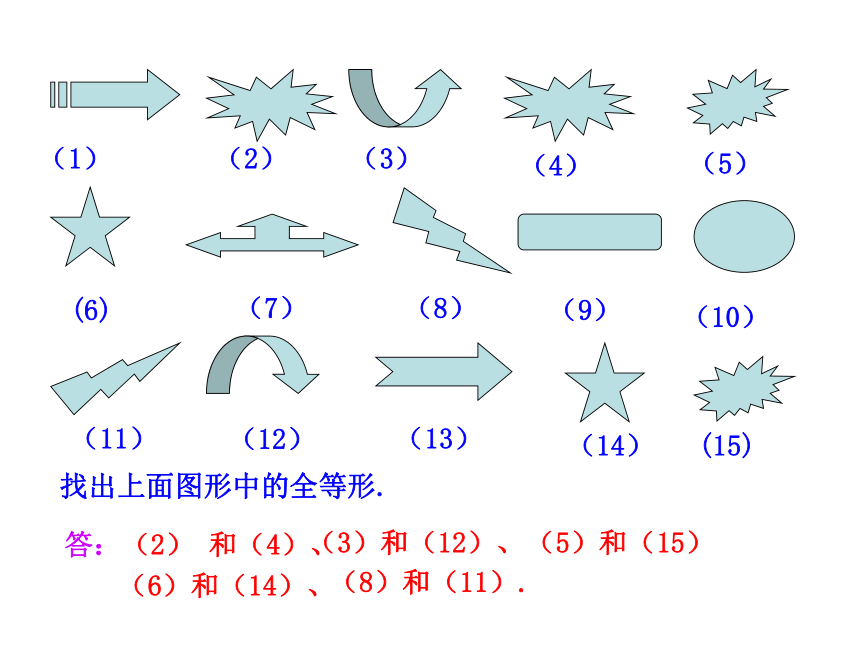
答:(2) 和(4)、
(5)和(15)
(3)和(12)、
(6)和(14)、
(8)和(11).
找出上面图形中的全等形.
(6)
(11)
(12)
(13)
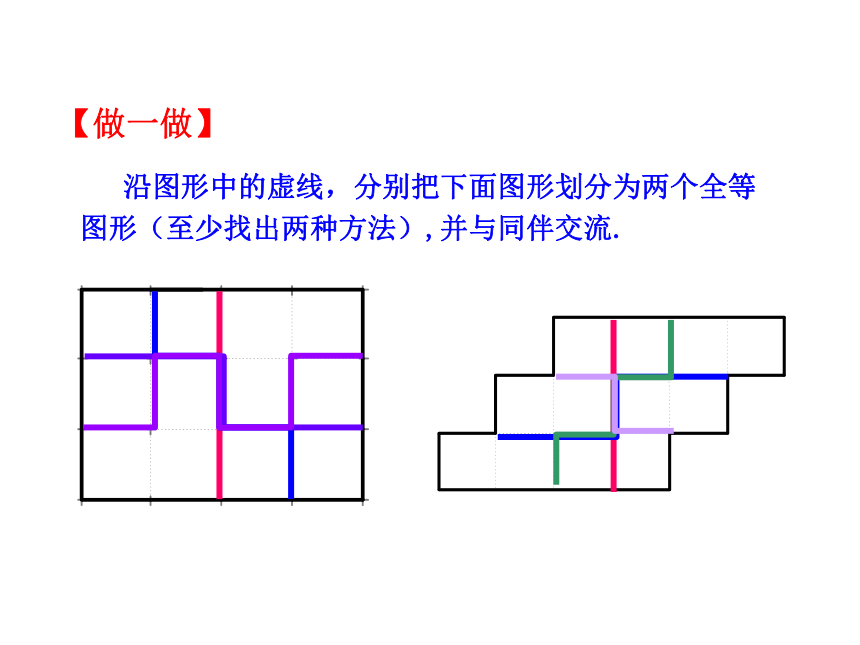
沿图形中的虚线,分别把下面图形划分为两个全等
图形(至少找出两种方法),并与同伴交流.
【做一做】
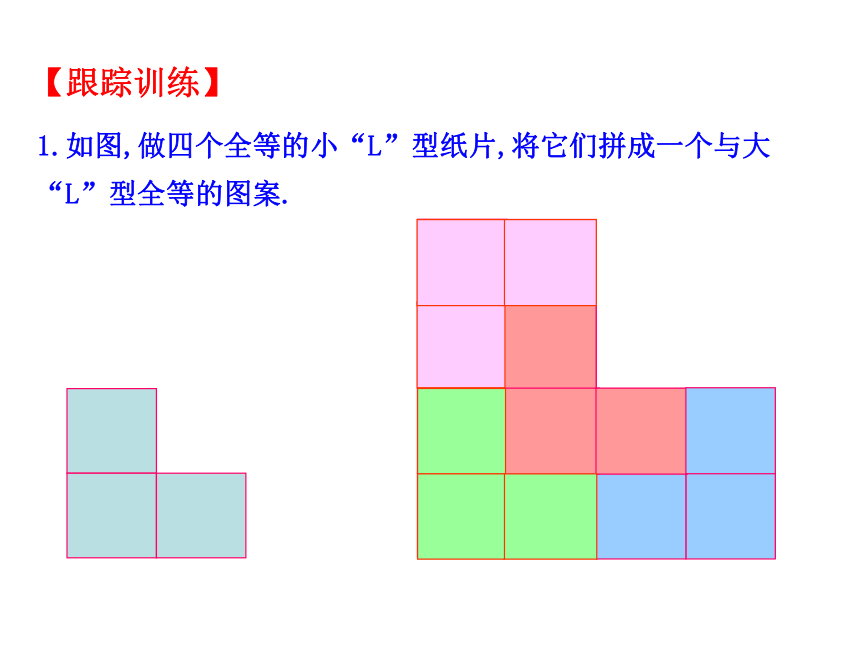
1.如图,做四个全等的小“L”型纸片,将它们拼成一个与大
“L”型全等的图案.
【跟踪训练】
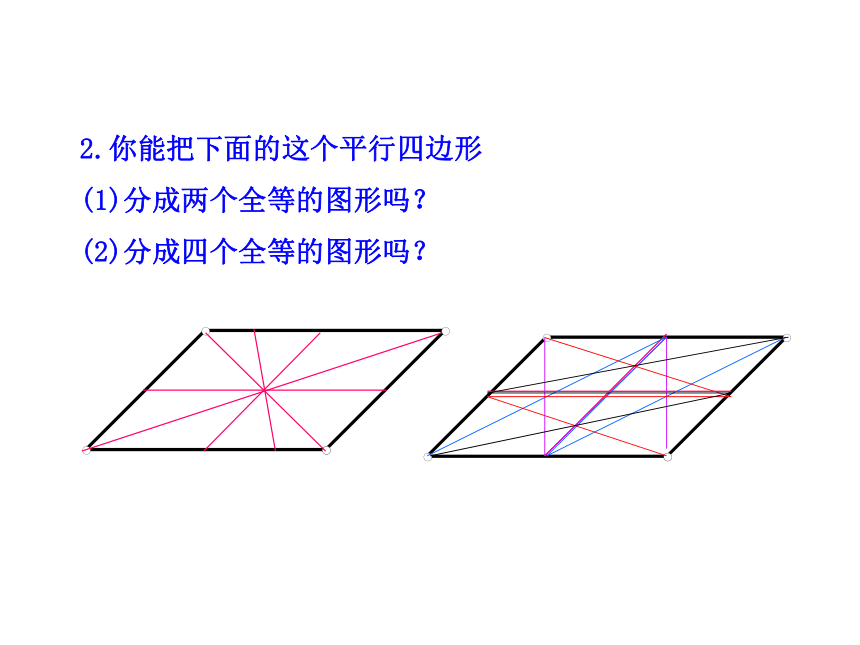
2.你能把下面的这个平行四边形
(1)分成两个全等的图形吗?
(2)分成四个全等的图形吗?
【相关概念】
能够完全重合的两个三角形叫做全等三角形.
当两个全等三角形完全重合时,互相重合的顶点叫做
对应顶点,互相重合的边叫做对应边,互相重合的角
叫做对应角.
表示方法:
△ABC≌△DEF
A
B
C
D
E
F
注意:要把表示对应顶点的字母写在对应的位置上,这样可
以比较容易地找出全等三角形的对应边和对应角.
全等三角形的
你能找到图中的对应点、对应边和对应角吗?
对应点:A与D,B与E,C与F 对应边:AB与DE,BC与EF,AC与DF
对应角:∠A与∠D,∠B与∠E,∠C与∠F
A
B
C
D
E
F
【想一想】
对应顶点:点A和点A1,点B和点B1,点C和点C1;
对应边:AB和A1B1,AC和A1C1,BC和B1C1;
对应角:∠A和∠A1, ∠B和∠B1, ∠C和∠C1.
A
B
C
A1
B1
C1
全等三角形的对应边相等,对应角相等.
如何找对应边、对应角?
1.全等三角形对应角所对的边是对应边;
全等三角形对应边所对的角是对应角.
2.有公共边的,公共边是对应边;
有公共角的,公共角是对应角.
3.在全等三角形中相等的边是对应边;
相等的角是对应角.
你能否直接从
△ABC≌ △DEF中判断出所有的对应顶点、对应边和对应角?
角
角
角
边
边
边
AB=DF
AC=DE
BC=FE
∠A=∠D
∠B=∠F
∠ACB=∠DEF
全等三角形的性质的运用
A
B
C
D
E
F
例 已知:如图,△ABC ≌△DEF.
(3)若∠A =100°,∠B =30°,求∠F 的度数.
解:∵ ∠A =100°,∠B =30°,
∴ ∠C =180°-∠A -∠B =50°.
∵ △DEF ≌△ABC ,
∴ ∠F =∠C =50°
(全等三角形的对应角相等).
2.如果△ABC≌△DEF,且△ABC的周长为100 cm,A,B分
别与D,E对应, AB=30 cm,DF=25 cm,则BC的长为( )
A.45 cm B.55 cm C.30 cm D. 25 cm
70°
3
A
【跟踪训练】
1.如果△ABC≌△ADC,AB=AD,∠B=70°,BC=3 cm,那么∠D=____,DC=____cm.
M
D
A
N
B
C
7cm
5 cm
3.如图,矩形ABCD沿AM折叠,使D点落在BC上的N点处,如
果AD=7cm,DM=5cm,则AN=___cm,NM=___cm.
7
5
1.能够完全重合的两个平面图形,叫做全等形.
2.全等形的形状和大小都相同,与位置无关.
3.全等三角形的对应边相等,对应角相等.
通过本课时的学习,需要我们掌握:
1.(铜仁·中考)如图,△ABC≌△DEF,BE=4,AE=1,则
DE的长是( )
A.5 B.4 C.3 D.2
【解析】选A.AB=BE+AE=4+1=5,因为△ABC≌△DEF,所以DE=AB=5.
D
E
A
B
F
C
2.如图,△ABC ≌△CDA,AB 与CD,BC 与
DA 是对应边,则下列结论错误的是( )
(A)∠ BAC =∠ DCA
(B)AB //DC
(C)∠ BCA =∠ DCA
(D)BC //DA
C
A
B
C
D
3.如图,已知△ AOC ≌ △BOD,求证:AC∥BD.
【证明】∵ △AOC ≌△BOD,
∴∠A= ∠B.(全等三角形的对应角相等)
∴ AC∥BD.(内错角相等,两直线平行)
【解析】因为△AEC≌△ABC,
所以∠E=∠B=30°,
∠ACE=∠ACB=85°,
∠EAC=∠BAC=180°- 30°-85°=65°.
4.如图:△ABC≌△AEC,
∠B=30°, ∠ACB=85°,求出
△AEC各内角的度数.
A
B
C
E
5.如图:△AOD≌△BOC,写出其中相等的角.
A
D
C
B
O
【解析】由全等三角形对应角相等可得:
∠A=∠B,
∠D=∠C,
∠DOA=∠COB.
6.如图,△ABC≌△DEF,∠B=25°,BC=6cm,AC=4cm ,
你能得出△DEF中哪些角的大小,哪些边的长度
A
B
C
D
E
F
因为△ABC≌△DEF,
所以∠E=∠B=25°,
EF=BC=6cm,
DF=AC=4cm.
【解析】
忘掉失败,不过要牢记失败中的教训.
第1章 全等三角形
1.1 全等三角形
这些是我们熟悉的图形,它们有什么特点?
同一张底片洗出
的同规格照片.
两张纸重合后的剪纸;
还有……?
举例
比一比:
裁下的纸板和
样板的形状、
大小是否 完
全 一样?能
完全重合吗?
思考
(7)
(6)
(3)
(1)
(2)
(4)
(5)
(8)
(9)
(10)
(11)
(12)
这些图形中有些是完全一样的,如果把它们叠在一起,它
们就能重合. 你能从图中找出这样的图形吗?
1.理解全等形的概念和特征.
2.能识别图形的全等,并能设计简单的图形.
3.掌握全等三角形的对应边相等、对应角相等.
4.能利用全等三角形的对应边相等、对应角相等进行简
单的推理和计算,解决一些实际问题.
全等形的形状相同,大小相等.
大小
相同
观察下面两组图形,它们是不是全等形?
形状
相同
不是
不是
能够完全重合的两个平面图形,叫做全等形.
观察下列各组图形是不是全等形
1.
2.
不是全等形
是全等形
(1)
(2)
(3)
(4)
(5)
(10)
(7)
(8)
(9)
(14)
(15)
答:(2) 和(4)、
(5)和(15)
(3)和(12)、
(6)和(14)、
(8)和(11).
找出上面图形中的全等形.
(6)
(11)
(12)
(13)
沿图形中的虚线,分别把下面图形划分为两个全等
图形(至少找出两种方法),并与同伴交流.
【做一做】
1.如图,做四个全等的小“L”型纸片,将它们拼成一个与大
“L”型全等的图案.
【跟踪训练】
2.你能把下面的这个平行四边形
(1)分成两个全等的图形吗?
(2)分成四个全等的图形吗?
【相关概念】
能够完全重合的两个三角形叫做全等三角形.
当两个全等三角形完全重合时,互相重合的顶点叫做
对应顶点,互相重合的边叫做对应边,互相重合的角
叫做对应角.
表示方法:
△ABC≌△DEF
A
B
C
D
E
F
注意:要把表示对应顶点的字母写在对应的位置上,这样可
以比较容易地找出全等三角形的对应边和对应角.
全等三角形的
你能找到图中的对应点、对应边和对应角吗?
对应点:A与D,B与E,C与F 对应边:AB与DE,BC与EF,AC与DF
对应角:∠A与∠D,∠B与∠E,∠C与∠F
A
B
C
D
E
F
【想一想】
对应顶点:点A和点A1,点B和点B1,点C和点C1;
对应边:AB和A1B1,AC和A1C1,BC和B1C1;
对应角:∠A和∠A1, ∠B和∠B1, ∠C和∠C1.
A
B
C
A1
B1
C1
全等三角形的对应边相等,对应角相等.
如何找对应边、对应角?
1.全等三角形对应角所对的边是对应边;
全等三角形对应边所对的角是对应角.
2.有公共边的,公共边是对应边;
有公共角的,公共角是对应角.
3.在全等三角形中相等的边是对应边;
相等的角是对应角.
你能否直接从
△ABC≌ △DEF中判断出所有的对应顶点、对应边和对应角?
角
角
角
边
边
边
AB=DF
AC=DE
BC=FE
∠A=∠D
∠B=∠F
∠ACB=∠DEF
全等三角形的性质的运用
A
B
C
D
E
F
例 已知:如图,△ABC ≌△DEF.
(3)若∠A =100°,∠B =30°,求∠F 的度数.
解:∵ ∠A =100°,∠B =30°,
∴ ∠C =180°-∠A -∠B =50°.
∵ △DEF ≌△ABC ,
∴ ∠F =∠C =50°
(全等三角形的对应角相等).
2.如果△ABC≌△DEF,且△ABC的周长为100 cm,A,B分
别与D,E对应, AB=30 cm,DF=25 cm,则BC的长为( )
A.45 cm B.55 cm C.30 cm D. 25 cm
70°
3
A
【跟踪训练】
1.如果△ABC≌△ADC,AB=AD,∠B=70°,BC=3 cm,那么∠D=____,DC=____cm.
M
D
A
N
B
C
7cm
5 cm
3.如图,矩形ABCD沿AM折叠,使D点落在BC上的N点处,如
果AD=7cm,DM=5cm,则AN=___cm,NM=___cm.
7
5
1.能够完全重合的两个平面图形,叫做全等形.
2.全等形的形状和大小都相同,与位置无关.
3.全等三角形的对应边相等,对应角相等.
通过本课时的学习,需要我们掌握:
1.(铜仁·中考)如图,△ABC≌△DEF,BE=4,AE=1,则
DE的长是( )
A.5 B.4 C.3 D.2
【解析】选A.AB=BE+AE=4+1=5,因为△ABC≌△DEF,所以DE=AB=5.
D
E
A
B
F
C
2.如图,△ABC ≌△CDA,AB 与CD,BC 与
DA 是对应边,则下列结论错误的是( )
(A)∠ BAC =∠ DCA
(B)AB //DC
(C)∠ BCA =∠ DCA
(D)BC //DA
C
A
B
C
D
3.如图,已知△ AOC ≌ △BOD,求证:AC∥BD.
【证明】∵ △AOC ≌△BOD,
∴∠A= ∠B.(全等三角形的对应角相等)
∴ AC∥BD.(内错角相等,两直线平行)
【解析】因为△AEC≌△ABC,
所以∠E=∠B=30°,
∠ACE=∠ACB=85°,
∠EAC=∠BAC=180°- 30°-85°=65°.
4.如图:△ABC≌△AEC,
∠B=30°, ∠ACB=85°,求出
△AEC各内角的度数.
A
B
C
E
5.如图:△AOD≌△BOC,写出其中相等的角.
A
D
C
B
O
【解析】由全等三角形对应角相等可得:
∠A=∠B,
∠D=∠C,
∠DOA=∠COB.
6.如图,△ABC≌△DEF,∠B=25°,BC=6cm,AC=4cm ,
你能得出△DEF中哪些角的大小,哪些边的长度
A
B
C
D
E
F
因为△ABC≌△DEF,
所以∠E=∠B=25°,
EF=BC=6cm,
DF=AC=4cm.
【解析】
忘掉失败,不过要牢记失败中的教训.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
