1.3 尺规作图 课件(共23张PPT) 2024-2025学年青岛版数学八年级上册
文档属性
| 名称 | 1.3 尺规作图 课件(共23张PPT) 2024-2025学年青岛版数学八年级上册 |
|
|
| 格式 | ppt | ||
| 文件大小 | 755.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
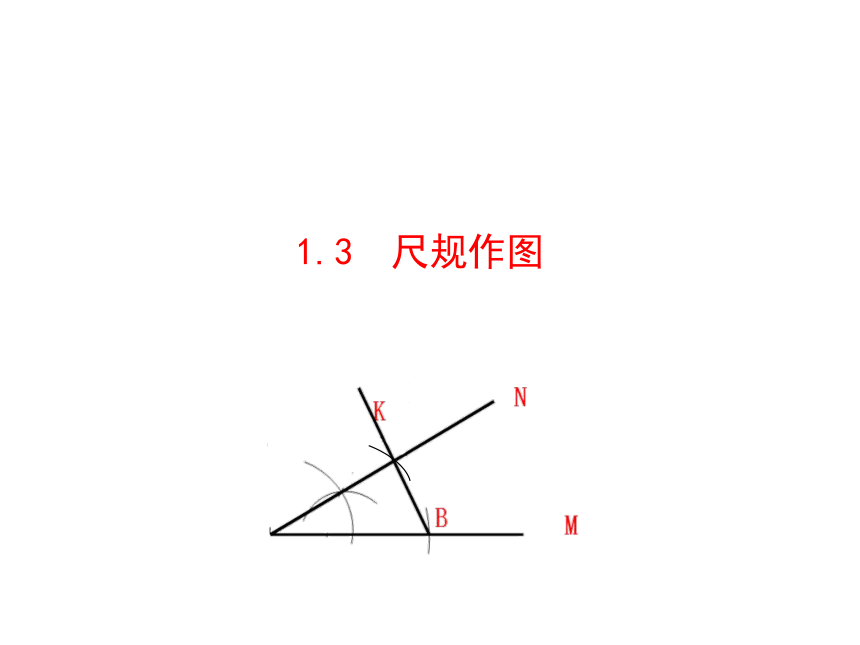
1.3 尺规作图
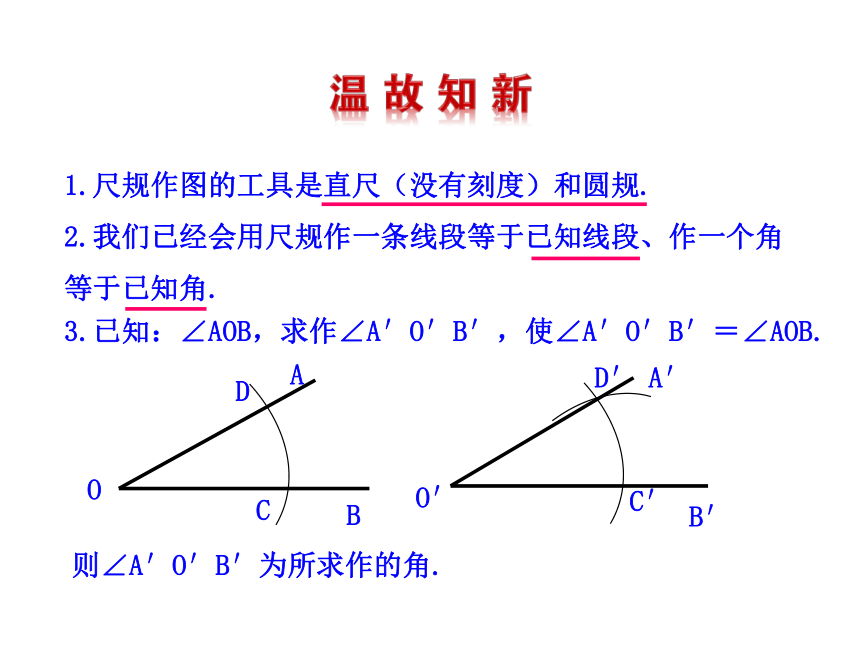
3.已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
2.我们已经会用尺规作一条线段等于已知线段、作一个角
等于已知角.
1.尺规作图的工具是直尺(没有刻度)和圆规.
O
B
A
C
D
O′
B′
A′
D′
C′
则∠A′O′B′为所求作的角.
1.经历尺规作图的实际操作过程,训练和提高学生的尺规
作图的技能,能根据条件作出三角形.
2.能结合三角形全等条件与同伴交流作图过程和结果的合
理性.
3.在学生利用尺规作图的过程中,培养学生的动手能力和
探索精神.
1.已知三角形的两边及其夹角,求作这个三角形.
已知:线段a, b, ∠α ,求作:△ABC,使BC=a,
AB=b, ∠ABC =∠α.
a
b
【做一做】
B
M
D′
E′
N
C
A
作法:(1)作∠MBN=∠ ,
(2)在射线BM上截取BC=a,在射线BN上截取BA=b,
(3)连接AC.
则△ABC为所求作的三角形.
作法与示范
剪下各自所作的三角形和同伴比较看是否全等?
能说出全等的理由吗?
两边及其夹角分别相等的两个三角形全等.
【探究新知】
2.已知三角形的两角及它们的夹边,求作三角形.
已知:∠α,∠β,线段c,求作:△ABC,使∠A=∠α,
∠B=∠β,AB=c.
β
c
作法示范
作法:(1)作线段AB=c
A
M
A
M
B
α
作法示范
A
M
A
M
B
(2)作∠NAB=∠α,
N
α
β
作法示范
A
M
A
M
B
N
K
C
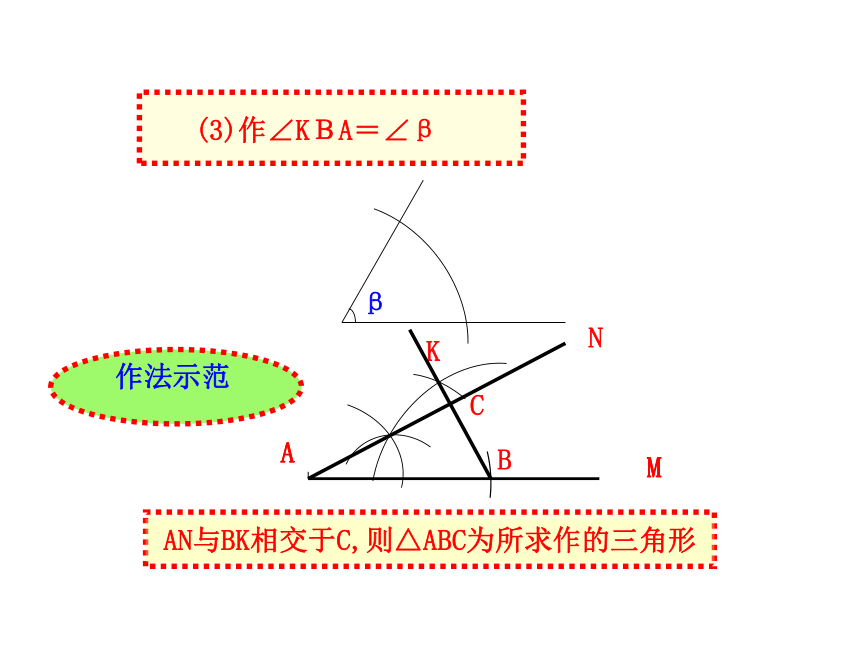
(3)作∠KBA=∠β
AN与BK相交于C,则△ABC为所求作的三角形
剪下各自所作的三角形和同伴比较看是否全等?
能说出全等的理由吗?
两角及其夹边分别相等的两个三角形全等.
【探究新知】
3.已知三角形的三边,求作三角形.
已知:线段a,b,c.
a
b
c
求作:△ABC,使BC=a, AC=b, AB=c.
作法示范
作法:(1)做线段BC=a,
B
M
A
C
(2)以C为圆心, b为半径画弧,
(3)以B为圆心, c为半径画弧,
两弧相交于点A,
(4)连接AB,AC.
则△ABC为所求作的三角形.
剪下各自所作的三角形和同伴比较看是否全等?
能说出全等的理由吗?
三边分别相等的两个三角形全等.
【探究新知】
如图,在△ABC中,BC=5cm,AC=3cm, AB=3.5cn,∠B=36°,
∠C=44°,请你选择适当数据,画与△ABC全等的三角形(不
写作法,但要从所画的三角形中标出用到的数据)
C
A
B
3.5cm
5cm
3cm
【跟踪训练】
B′
M
C′
A′
3.5cm
5cm
3cm
【解析】
已知:线段m,n,锐角∠α.
求作:△ABC,使AB=m,角平分线AD= n,∠CAB= ∠α
α
m
n
A
M
N
(1)作∠MAN = ∠ α
【归纳升华】
A
M
N
B
(2) 以A为圆心, m为半径画弧交AM于B,交AN于K
K
α
m
n
A
M
N
B
C
P
D
(1)作∠MAN = ∠ α
(2) 以A为圆心, m长为半径画弧
K
(3)分别以B,K为圆心,大于BK的距离一半的长为半径画弧,两弧交于P点
(4)作射线AP
(5) 在射线AP上截取AD = n
连接BD并延长交射线AK于点C
则△ABC为所求作的三角形
α
m
n
1.已知两边及其夹角作三角形的方法
2.已知两角及其夹边作三角形的方法
3.已知三边作三角形的方法
用尺规作三角形的方法
4.已知两角及一边作三角形的方法
通过本课时的学习,需要我们掌握:
1.利用尺规不能作出唯一的三角形的是( )
A.已知三边 B.已知两边及其夹角
C.已知两角及其夹边 D.已知两边及其中一边的对角
2.利用尺规不可作的直角三角形是( )
A.已知斜边及一条直角边 B.已知两条直角边
C.已知两锐角 D.已知一锐角及一直角边
3.以下列线段为边能作三角形的是( )
A.2cm、3cm、5cm B.4cm、4cm、9cm
C.1cm、2cm、3cm D.2cm、3cm、4cm
D
C
D
4.下列作图中,只用无刻度的直尺就能够作出的是( )
A.连接A,B两点并延长
B.作∠MON等于已知角∠α
C.作线段AB等于已知线段
D.作已知角的2倍角
【解析】选A.因为B、C、D三个选项都必须用直尺与圆规方能完成,二者缺一不可,A选项只用直尺即可.
5.已知三角形的两边及其夹角,作三角形时,第一步应为
( )
A.作一条线段等于已知线段
B.作一个角等于已知角
C.作两条线段等于已知角的两边
D.作一条线段等于已知线段或作一个角等于已知角
【解析】选B.根据“SAS”,作三角形的第一步应作一个角
等于已知角.
6.(杭州·中考) 四条线段a,b,c,d,如图,a:b:c:d =1:2:3:4.选择其中的三条线段为边作一个三角形(尺规作图,要求保留作图痕迹,不必写出作法);
【解析】如图
速度就是一切,它是竞争不可或缺的因素.
1.3 尺规作图
3.已知:∠AOB,求作∠A′O′B′,使∠A′O′B′=∠AOB.
2.我们已经会用尺规作一条线段等于已知线段、作一个角
等于已知角.
1.尺规作图的工具是直尺(没有刻度)和圆规.
O
B
A
C
D
O′
B′
A′
D′
C′
则∠A′O′B′为所求作的角.
1.经历尺规作图的实际操作过程,训练和提高学生的尺规
作图的技能,能根据条件作出三角形.
2.能结合三角形全等条件与同伴交流作图过程和结果的合
理性.
3.在学生利用尺规作图的过程中,培养学生的动手能力和
探索精神.
1.已知三角形的两边及其夹角,求作这个三角形.
已知:线段a, b, ∠α ,求作:△ABC,使BC=a,
AB=b, ∠ABC =∠α.
a
b
【做一做】
B
M
D′
E′
N
C
A
作法:(1)作∠MBN=∠ ,
(2)在射线BM上截取BC=a,在射线BN上截取BA=b,
(3)连接AC.
则△ABC为所求作的三角形.
作法与示范
剪下各自所作的三角形和同伴比较看是否全等?
能说出全等的理由吗?
两边及其夹角分别相等的两个三角形全等.
【探究新知】
2.已知三角形的两角及它们的夹边,求作三角形.
已知:∠α,∠β,线段c,求作:△ABC,使∠A=∠α,
∠B=∠β,AB=c.
β
c
作法示范
作法:(1)作线段AB=c
A
M
A
M
B
α
作法示范
A
M
A
M
B
(2)作∠NAB=∠α,
N
α
β
作法示范
A
M
A
M
B
N
K
C
(3)作∠KBA=∠β
AN与BK相交于C,则△ABC为所求作的三角形
剪下各自所作的三角形和同伴比较看是否全等?
能说出全等的理由吗?
两角及其夹边分别相等的两个三角形全等.
【探究新知】
3.已知三角形的三边,求作三角形.
已知:线段a,b,c.
a
b
c
求作:△ABC,使BC=a, AC=b, AB=c.
作法示范
作法:(1)做线段BC=a,
B
M
A
C
(2)以C为圆心, b为半径画弧,
(3)以B为圆心, c为半径画弧,
两弧相交于点A,
(4)连接AB,AC.
则△ABC为所求作的三角形.
剪下各自所作的三角形和同伴比较看是否全等?
能说出全等的理由吗?
三边分别相等的两个三角形全等.
【探究新知】
如图,在△ABC中,BC=5cm,AC=3cm, AB=3.5cn,∠B=36°,
∠C=44°,请你选择适当数据,画与△ABC全等的三角形(不
写作法,但要从所画的三角形中标出用到的数据)
C
A
B
3.5cm
5cm
3cm
【跟踪训练】
B′
M
C′
A′
3.5cm
5cm
3cm
【解析】
已知:线段m,n,锐角∠α.
求作:△ABC,使AB=m,角平分线AD= n,∠CAB= ∠α
α
m
n
A
M
N
(1)作∠MAN = ∠ α
【归纳升华】
A
M
N
B
(2) 以A为圆心, m为半径画弧交AM于B,交AN于K
K
α
m
n
A
M
N
B
C
P
D
(1)作∠MAN = ∠ α
(2) 以A为圆心, m长为半径画弧
K
(3)分别以B,K为圆心,大于BK的距离一半的长为半径画弧,两弧交于P点
(4)作射线AP
(5) 在射线AP上截取AD = n
连接BD并延长交射线AK于点C
则△ABC为所求作的三角形
α
m
n
1.已知两边及其夹角作三角形的方法
2.已知两角及其夹边作三角形的方法
3.已知三边作三角形的方法
用尺规作三角形的方法
4.已知两角及一边作三角形的方法
通过本课时的学习,需要我们掌握:
1.利用尺规不能作出唯一的三角形的是( )
A.已知三边 B.已知两边及其夹角
C.已知两角及其夹边 D.已知两边及其中一边的对角
2.利用尺规不可作的直角三角形是( )
A.已知斜边及一条直角边 B.已知两条直角边
C.已知两锐角 D.已知一锐角及一直角边
3.以下列线段为边能作三角形的是( )
A.2cm、3cm、5cm B.4cm、4cm、9cm
C.1cm、2cm、3cm D.2cm、3cm、4cm
D
C
D
4.下列作图中,只用无刻度的直尺就能够作出的是( )
A.连接A,B两点并延长
B.作∠MON等于已知角∠α
C.作线段AB等于已知线段
D.作已知角的2倍角
【解析】选A.因为B、C、D三个选项都必须用直尺与圆规方能完成,二者缺一不可,A选项只用直尺即可.
5.已知三角形的两边及其夹角,作三角形时,第一步应为
( )
A.作一条线段等于已知线段
B.作一个角等于已知角
C.作两条线段等于已知角的两边
D.作一条线段等于已知线段或作一个角等于已知角
【解析】选B.根据“SAS”,作三角形的第一步应作一个角
等于已知角.
6.(杭州·中考) 四条线段a,b,c,d,如图,a:b:c:d =1:2:3:4.选择其中的三条线段为边作一个三角形(尺规作图,要求保留作图痕迹,不必写出作法);
【解析】如图
速度就是一切,它是竞争不可或缺的因素.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
