1.1 相似多边形 课件(共30张PPT) 2024-2025学年青岛版初中数学九年级上册
文档属性
| 名称 | 1.1 相似多边形 课件(共30张PPT) 2024-2025学年青岛版初中数学九年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 19:05:29 | ||
图片预览









文档简介
(共30张PPT)
第1章 图形的相似
1.1 相似多边形
问题:用同一张底片洗出不同尺寸的照片,两张图片相似吗
1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形的概念.
2.理解相似多边形的性质和判定.
请观察下面几组图片
你能发现它们有什么特点吗
形状相同,大小不同
我们把这种形状相同的平面图形叫做相似形.
定义:
两两相似的几何图形
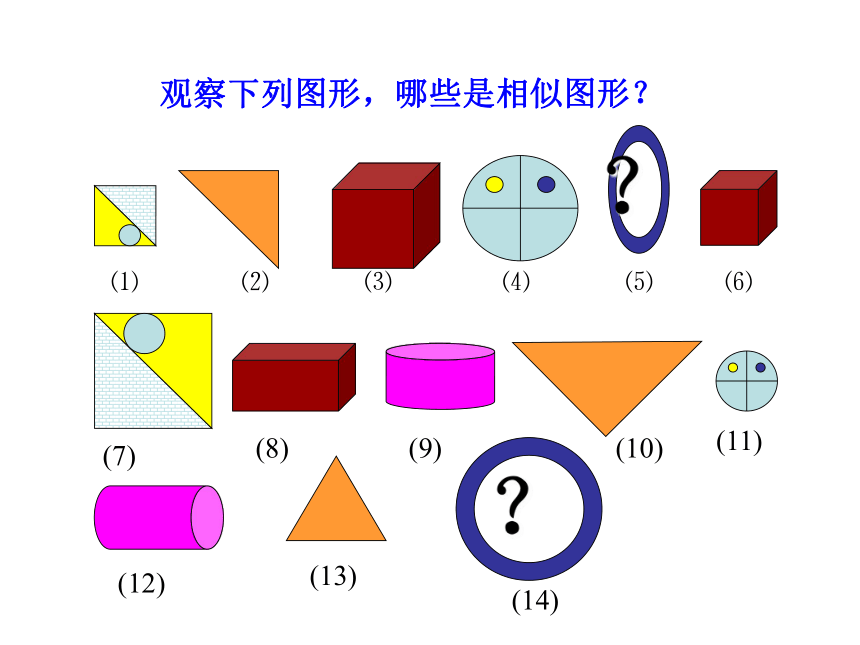
观察下列图形,哪些是相似图形?
(14)
(12)
(13)
⑴
⑵
⑶
(7)
(9)
(8)
?
⑷
⑹
⑸
?
(10)
(11)
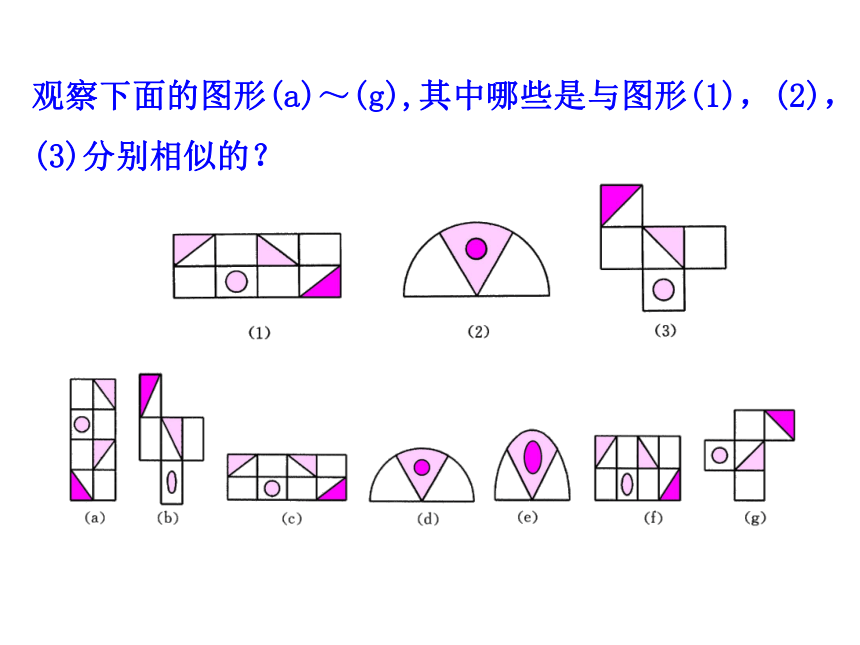
观察下面的图形(a)~(g),其中哪些是与图形(1),(2),(3)分别相似的?
A B D F
下列图形中____与_____是相似的.
(1) (2) (3) (4)
选一选
(1) (4)
将下列图形分成四块,使它们的大小、形状完全相同,且与原图形相似,你会分吗?怎样分?
图(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对应角相等
对应边的比相等
图
对于图(2)中的两个相似的正六边形,你是否也能得到类似的结论?
对应角相等
对应边的比相等
能
图
图(1)是两个相似的三角形,它们的对应角有什么关系?
对应边的比是否相等?
对于图(2)中两个相似的四边形,它们的对应角、对应边
是否有同样的结论?
对应角相等
对应边的比相等
有
对应角相等
对应边的比相等
图(1)
图(2)
相似多边形对应边的比称为相似比
相似多边形对应角相等,对应边的比相等.
全等
相似比为1时,相似的两个图形有什么关系?
相似多边形的判断方法:
若两个多边形满足对应角相等,对应边的比相等,
则这两个多边形相似.
相似多边形的性质:
【例】如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
【例题】
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
【解析】四边形ABCD和EFGH相似,它们的对应角相等.
由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
四边形ABCD和EFGH相似,它们的对应边的比
相等.
由此可得
解得x=28.
如图矩形草坪长20 m,宽10 m,沿草坪四周有1 m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
∴不相似
【跟踪训练】
1. 经过这节课的学习,你有哪些收获?
2. 你想进一步探究的问题是什么?
1.(南平·中考)下列说法中,错误的是( )
A.等边三角形都相似
B.等腰直角三角形都相似
C.矩形都相似
D.正方形都相似
C
2.(烟台·中考)手工制作课上,小红利用一些花布的边
角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空
心不等边三角形、等边三角形、正方形、矩形花边框,其
中,每个图案花边的宽度都相等,那么,每个图案中花边
的内外边缘所围成的几何图形不相似的是( )
D
3.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】选C.设阴影部分的宽为x cm,因为两个矩形相
似,所以 ,则x=2 cm,则留下的矩形的面积
S=2×4=8(cm2).
4.一个五边形的边长分别是2,3,4,5,6,另一个
和它相似的五边形的最短边长为6,则另一个五边形
的最长边长为____.
【解析】设另一个五边形的最长边长为x,则有
解得x=18.
答案:18
5. 如图所示的两个五边形相似,求未知边a,b,c,d的长度.
5
3
2
c
d
7.5
b
a
6
9
【解析】由图可知两图形的相似比为:
b = 4.5
a = 3
c = 4
d = 6
,
,
;
;
,
,
;
,
.
信念!有信念的人经得起任何风暴。
——奥维德
第1章 图形的相似
1.1 相似多边形
问题:用同一张底片洗出不同尺寸的照片,两张图片相似吗
1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形的概念.
2.理解相似多边形的性质和判定.
请观察下面几组图片
你能发现它们有什么特点吗
形状相同,大小不同
我们把这种形状相同的平面图形叫做相似形.
定义:
两两相似的几何图形
观察下列图形,哪些是相似图形?
(14)
(12)
(13)
⑴
⑵
⑶
(7)
(9)
(8)
?
⑷
⑹
⑸
?
(10)
(11)
观察下面的图形(a)~(g),其中哪些是与图形(1),(2),(3)分别相似的?
A B D F
下列图形中____与_____是相似的.
(1) (2) (3) (4)
选一选
(1) (4)
将下列图形分成四块,使它们的大小、形状完全相同,且与原图形相似,你会分吗?怎样分?
图(1)中的△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
对应角相等
对应边的比相等
图
对于图(2)中的两个相似的正六边形,你是否也能得到类似的结论?
对应角相等
对应边的比相等
能
图
图(1)是两个相似的三角形,它们的对应角有什么关系?
对应边的比是否相等?
对于图(2)中两个相似的四边形,它们的对应角、对应边
是否有同样的结论?
对应角相等
对应边的比相等
有
对应角相等
对应边的比相等
图(1)
图(2)
相似多边形对应边的比称为相似比
相似多边形对应角相等,对应边的比相等.
全等
相似比为1时,相似的两个图形有什么关系?
相似多边形的判断方法:
若两个多边形满足对应角相等,对应边的比相等,
则这两个多边形相似.
相似多边形的性质:
【例】如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
【例题】
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°
【解析】四边形ABCD和EFGH相似,它们的对应角相等.
由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
四边形ABCD和EFGH相似,它们的对应边的比
相等.
由此可得
解得x=28.
如图矩形草坪长20 m,宽10 m,沿草坪四周有1 m宽的环形小路,小路内外边缘所成的矩形EFGH和矩形ABCD是否相似
A
F
E
H
G
D
C
B
∴不相似
【跟踪训练】
1. 经过这节课的学习,你有哪些收获?
2. 你想进一步探究的问题是什么?
1.(南平·中考)下列说法中,错误的是( )
A.等边三角形都相似
B.等腰直角三角形都相似
C.矩形都相似
D.正方形都相似
C
2.(烟台·中考)手工制作课上,小红利用一些花布的边
角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空
心不等边三角形、等边三角形、正方形、矩形花边框,其
中,每个图案花边的宽度都相等,那么,每个图案中花边
的内外边缘所围成的几何图形不相似的是( )
D
3.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形的面积是( )
A.2 cm2 B.4 cm2 C.8 cm2 D.16 cm2
【解析】选C.设阴影部分的宽为x cm,因为两个矩形相
似,所以 ,则x=2 cm,则留下的矩形的面积
S=2×4=8(cm2).
4.一个五边形的边长分别是2,3,4,5,6,另一个
和它相似的五边形的最短边长为6,则另一个五边形
的最长边长为____.
【解析】设另一个五边形的最长边长为x,则有
解得x=18.
答案:18
5. 如图所示的两个五边形相似,求未知边a,b,c,d的长度.
5
3
2
c
d
7.5
b
a
6
9
【解析】由图可知两图形的相似比为:
b = 4.5
a = 3
c = 4
d = 6
,
,
;
;
,
,
;
,
.
信念!有信念的人经得起任何风暴。
——奥维德
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
