2025年中考数学总复习40微专题 尺规作图 学案(含答案)
文档属性
| 名称 | 2025年中考数学总复习40微专题 尺规作图 学案(含答案) | 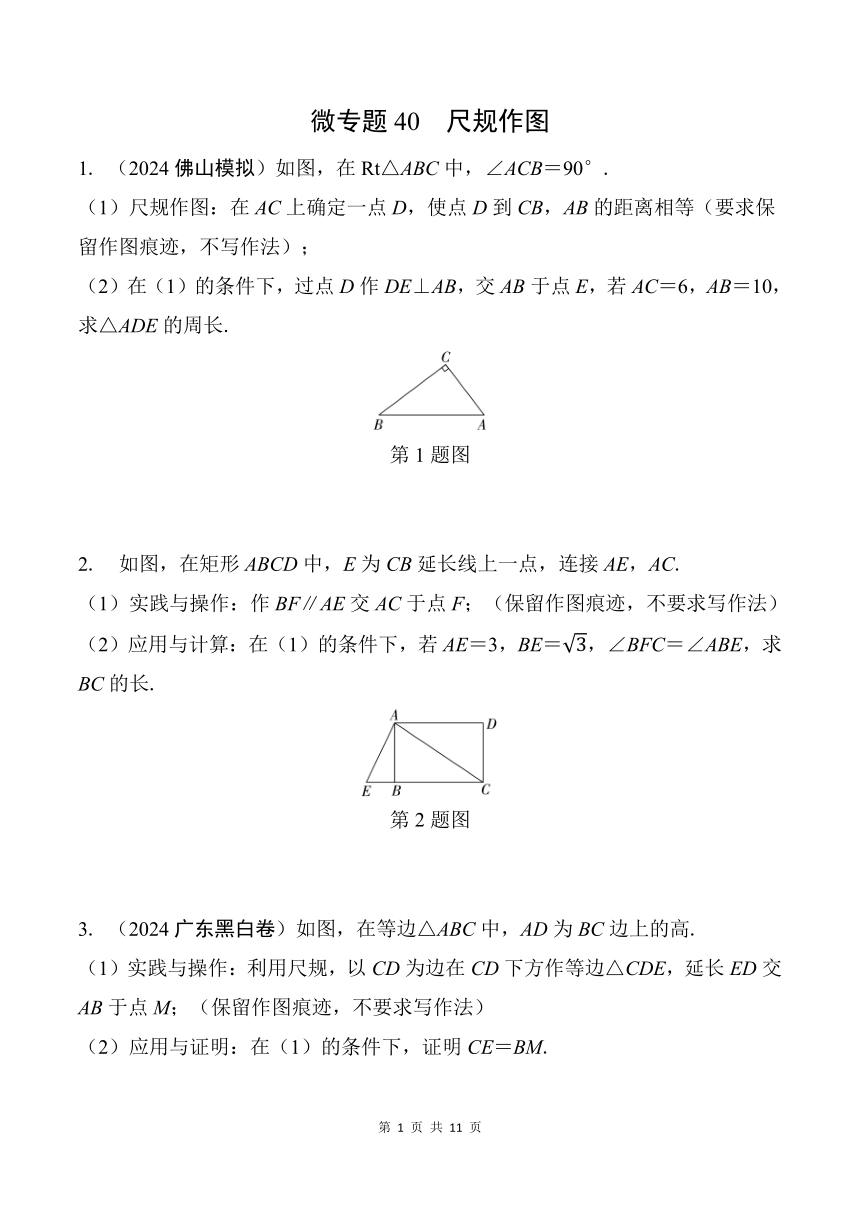 | |
| 格式 | docx | ||
| 文件大小 | 197.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 19:34:12 | ||
图片预览





文档简介
微专题40 尺规作图
1. (2024佛山模拟)如图,在Rt△ABC中,∠ACB=90°.
(1)尺规作图:在AC上确定一点D,使点D到CB,AB的距离相等(要求保留作图痕迹,不写作法);
(2)在(1)的条件下,过点D作DE⊥AB,交AB于点E,若AC=6,AB=10,求△ADE的周长.
第1题图
2. 如图,在矩形ABCD中,E为CB延长线上一点,连接AE,AC.
(1)实践与操作:作BF∥AE交AC于点F;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,若AE=3,BE=,∠BFC=∠ABE,求BC的长.
第2题图
3. (2024广东黑白卷)如图,在等边△ABC中,AD为BC边上的高.
(1)实践与操作:利用尺规,以CD为边在CD下方作等边△CDE,延长ED交AB于点M;(保留作图痕迹,不要求写作法)
(2)应用与证明:在(1)的条件下,证明CE=BM.
第3题图
4. (2024广州)如图,在Rt△ABC中,∠B=90°.
(1)尺规作图:作AC边上的中线BO(保留作图痕迹,不写作法);
(2)在(1)所作的图中,将中线BO绕点O逆时针旋转180°得到DO,连接AD,CD,求证:四边形ABCD是矩形.
第4题图
5. 如图,△ABC为等腰三角形.
(1)实践与操作:求作菱形AEDF,使得∠A为菱形的一个内角,点D,E,F分别在边BC,AB,AC上;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,若AB=AC=10,BC=8,求菱形AEDF的面积.
第5题图
6. 如图,在Rt△ABC中,∠ABC=90°.
(1)实践与操作:在边AC上取点O,以OC为半径作☉O,使得☉O与AB相切;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,若AO=BC,求的值.
第6题图
7. (2024香洲区二模)如图,在△ABC中,∠ABC=90°+∠A,以AB为直径的☉O交AC于D.
(1)实践与操作:过点B作EB⊥AB,交AC于点E;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,当BE=OA,BC=10时,求DE的长度.
第7题图
8. (2024佛山一模)综合与实践
数学活动课上,同学们用尺规作图法探究在菱形内部作一点到该菱形三个顶点的距离相等.
【动手操作】如图,已知菱形ABCD,求作点E,使得点E到三个顶点A,D,C的距离相等.小红同学设计如下作图步骤;
①连接BD;
②分别以点A,D为圆心,大于AD的长为半径分别在AD的上方与下方作弧;AD上方两弧交于点M,下方两弧交于点N,作直线MN交BD于点E;
③连接AE,EC,则EA=ED=EC.
(1)根据小红同学设计的尺规作图步骤,在图中完成作图过程.(保留作图痕迹,不要求写作法).
【证明结论】
(2)证明:EA=ED=EC.
【拓展延伸】
(3)当∠ABC=72°时,求△EBC与△EAD的面积比.
1. 解:(1)如解图,点D即为所求;
第1题解图
(2)如解图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,
∴BC=8,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∵∠C=90°=∠BED,BD=BD,
∴△BCD≌△BED(AAS),
∴CD=DE,BC=BE,
∴EA=BA-BE=BA-CB=2,
∴△ADE的周长=AD+DE+AE=AD+CD+AE=AC+AE=6+2=8.
2. 解:(1)如解图①或解图②,点F即为所求;(作法不唯一)
第2题解图
(2)∵BF∥AE,
∴∠BFC=∠EAC,
∵∠BFC=∠ABE,
∴∠EAC=∠ABE,
∵∠AEC=∠AEB,
∴△ABE∽△CAE,
∴=,∴=,
解得CE=3,
∴BC=CE-BE=2.
3. (1)解:如解图①,△CDE即为所求作的三角形;(答案不唯一)
一题多解法
如解图②,△CDE即为所求作的三角形.
第3题解图
(2)证明:∵△ABC为等边三角形,AD为BC边上的高,
∴∠B=∠ACB=60°,BD=CD,
∵△CDE为等边三角形,
∴∠ECD=60°,∴∠B=∠ECD,
∵∠MDB=∠EDC,
∴△BMD≌△CED(ASA),
∴CE=BM.
4. (1)解:如解图①,线段BO即为所求;
第4题解图①
(2)证明:如解图②,由题可得AO=CO,由旋转可得BO=DO,
∴四边形ABCD为平行四边形,
∵∠ABC=90°,
∴四边形ABCD为矩形.
第4题解图②
5. 解:(1)如解图,菱形AEDF即为所求(作法不唯一,合理即可);
第5题解图
(2)如解图,设AD与EF交于点O,
∵AD是∠BAC的平分线,
∴AD⊥BC,BD=CD=BC=4.
在Rt△ABD中,AD===2,
∵EF⊥AD,
∴EF∥BC.
∵AO=OD,
∴E,F分别为AB和AC的中点,
∴EF=BC=4,
∴S菱形AEDF=AD·EF=4.
6. 解:(1)如解图①②,☉O即为所求;
第6题解图
(2)如解图③,连接OD,
∵☉O与AB相切,
∴OD=OC,OD⊥AB,
∵∠ABC=90°,
∴OD∥BC,
∴△ADO∽△ABC,
∴==.
∵AO=BC,OD=OC,
∴==,
即AO2=OC2+OC·AO,
∴=+,
即1=()2+,
设=a,则1=a2+a,
整理得a2+a-1=0,
解得a=(负值已舍去),
∴=.
第6题解图③
7. 解:(1)如解图,BE即为所求;
第7题解图
(2)如解图,连接DB.
∵AB⊥BE,
∴∠ABE=90°,
∵∠ABC=∠ABE+∠EBC=90°+∠A,
∴∠A=∠EBC,
∵∠C=∠C,
∴△CBE∽△CAB,
∴====,
∵BC=10,
∴CE=5,CA=20,
∴AE=AC-CE=20-5=15,
∵AB是☉O的直径,
∴∠ADB=∠BDE=90°,
∵∠A+∠ABD=90°,∠ABD+∠DBE=90°,
∴∠A=∠DBE,
∴△ADB∽△BDE,
∴===2,
∴BD=2DE,AD=2BD=4DE,
∴DE=AE=3.
8. (1)解:根据小红同学设计,完成作图过程如解图所示;
第8题解图
(2)证明:在菱形ABCD中,∠ADE=∠CDE,AD=DC,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=EC,
∵MN垂直平分AD,
∴AE=DE,
∴AE=DE=EC;
(3)解:∵在菱形ABCD中,∠ABC=72°,
∴∠ABD=∠DBC=36°,
∵AD∥BC,
∴∠ADB=∠DBC=36°,∠DAB=180°-∠ABC=108°.
∵AE=DE,
∴∠EAD=∠ADB=36°,
∴∠EAD=∠ABD=36°,
∵∠ADE=∠BDA,
∴△ADE∽△BDA,
∴=,即AD2=BD·DE.
∵∠BAE=∠BAD-∠EAD=72°,∠BEA=∠EAD+∠ADE=72°,
∴∠BAE=∠BEA,
∴BE=AB.
设AB=x=BE,DE=a(其中x,a>0),
则x2=(x+a)·a,
∴x2-ax-a2=0,解得x=a或x=a(舍去),
∴=,
设点A到BD距离为h,则点C到BD的距离为h,
∴S△AED=DE·h,
S△EDC=DE·h,
∴S△AED=S△EDC,
∴====.
1. (2024佛山模拟)如图,在Rt△ABC中,∠ACB=90°.
(1)尺规作图:在AC上确定一点D,使点D到CB,AB的距离相等(要求保留作图痕迹,不写作法);
(2)在(1)的条件下,过点D作DE⊥AB,交AB于点E,若AC=6,AB=10,求△ADE的周长.
第1题图
2. 如图,在矩形ABCD中,E为CB延长线上一点,连接AE,AC.
(1)实践与操作:作BF∥AE交AC于点F;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,若AE=3,BE=,∠BFC=∠ABE,求BC的长.
第2题图
3. (2024广东黑白卷)如图,在等边△ABC中,AD为BC边上的高.
(1)实践与操作:利用尺规,以CD为边在CD下方作等边△CDE,延长ED交AB于点M;(保留作图痕迹,不要求写作法)
(2)应用与证明:在(1)的条件下,证明CE=BM.
第3题图
4. (2024广州)如图,在Rt△ABC中,∠B=90°.
(1)尺规作图:作AC边上的中线BO(保留作图痕迹,不写作法);
(2)在(1)所作的图中,将中线BO绕点O逆时针旋转180°得到DO,连接AD,CD,求证:四边形ABCD是矩形.
第4题图
5. 如图,△ABC为等腰三角形.
(1)实践与操作:求作菱形AEDF,使得∠A为菱形的一个内角,点D,E,F分别在边BC,AB,AC上;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,若AB=AC=10,BC=8,求菱形AEDF的面积.
第5题图
6. 如图,在Rt△ABC中,∠ABC=90°.
(1)实践与操作:在边AC上取点O,以OC为半径作☉O,使得☉O与AB相切;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,若AO=BC,求的值.
第6题图
7. (2024香洲区二模)如图,在△ABC中,∠ABC=90°+∠A,以AB为直径的☉O交AC于D.
(1)实践与操作:过点B作EB⊥AB,交AC于点E;(保留作图痕迹,不要求写作法)
(2)应用与计算:在(1)的条件下,当BE=OA,BC=10时,求DE的长度.
第7题图
8. (2024佛山一模)综合与实践
数学活动课上,同学们用尺规作图法探究在菱形内部作一点到该菱形三个顶点的距离相等.
【动手操作】如图,已知菱形ABCD,求作点E,使得点E到三个顶点A,D,C的距离相等.小红同学设计如下作图步骤;
①连接BD;
②分别以点A,D为圆心,大于AD的长为半径分别在AD的上方与下方作弧;AD上方两弧交于点M,下方两弧交于点N,作直线MN交BD于点E;
③连接AE,EC,则EA=ED=EC.
(1)根据小红同学设计的尺规作图步骤,在图中完成作图过程.(保留作图痕迹,不要求写作法).
【证明结论】
(2)证明:EA=ED=EC.
【拓展延伸】
(3)当∠ABC=72°时,求△EBC与△EAD的面积比.
1. 解:(1)如解图,点D即为所求;
第1题解图
(2)如解图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,
∴BC=8,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∵∠C=90°=∠BED,BD=BD,
∴△BCD≌△BED(AAS),
∴CD=DE,BC=BE,
∴EA=BA-BE=BA-CB=2,
∴△ADE的周长=AD+DE+AE=AD+CD+AE=AC+AE=6+2=8.
2. 解:(1)如解图①或解图②,点F即为所求;(作法不唯一)
第2题解图
(2)∵BF∥AE,
∴∠BFC=∠EAC,
∵∠BFC=∠ABE,
∴∠EAC=∠ABE,
∵∠AEC=∠AEB,
∴△ABE∽△CAE,
∴=,∴=,
解得CE=3,
∴BC=CE-BE=2.
3. (1)解:如解图①,△CDE即为所求作的三角形;(答案不唯一)
一题多解法
如解图②,△CDE即为所求作的三角形.
第3题解图
(2)证明:∵△ABC为等边三角形,AD为BC边上的高,
∴∠B=∠ACB=60°,BD=CD,
∵△CDE为等边三角形,
∴∠ECD=60°,∴∠B=∠ECD,
∵∠MDB=∠EDC,
∴△BMD≌△CED(ASA),
∴CE=BM.
4. (1)解:如解图①,线段BO即为所求;
第4题解图①
(2)证明:如解图②,由题可得AO=CO,由旋转可得BO=DO,
∴四边形ABCD为平行四边形,
∵∠ABC=90°,
∴四边形ABCD为矩形.
第4题解图②
5. 解:(1)如解图,菱形AEDF即为所求(作法不唯一,合理即可);
第5题解图
(2)如解图,设AD与EF交于点O,
∵AD是∠BAC的平分线,
∴AD⊥BC,BD=CD=BC=4.
在Rt△ABD中,AD===2,
∵EF⊥AD,
∴EF∥BC.
∵AO=OD,
∴E,F分别为AB和AC的中点,
∴EF=BC=4,
∴S菱形AEDF=AD·EF=4.
6. 解:(1)如解图①②,☉O即为所求;
第6题解图
(2)如解图③,连接OD,
∵☉O与AB相切,
∴OD=OC,OD⊥AB,
∵∠ABC=90°,
∴OD∥BC,
∴△ADO∽△ABC,
∴==.
∵AO=BC,OD=OC,
∴==,
即AO2=OC2+OC·AO,
∴=+,
即1=()2+,
设=a,则1=a2+a,
整理得a2+a-1=0,
解得a=(负值已舍去),
∴=.
第6题解图③
7. 解:(1)如解图,BE即为所求;
第7题解图
(2)如解图,连接DB.
∵AB⊥BE,
∴∠ABE=90°,
∵∠ABC=∠ABE+∠EBC=90°+∠A,
∴∠A=∠EBC,
∵∠C=∠C,
∴△CBE∽△CAB,
∴====,
∵BC=10,
∴CE=5,CA=20,
∴AE=AC-CE=20-5=15,
∵AB是☉O的直径,
∴∠ADB=∠BDE=90°,
∵∠A+∠ABD=90°,∠ABD+∠DBE=90°,
∴∠A=∠DBE,
∴△ADB∽△BDE,
∴===2,
∴BD=2DE,AD=2BD=4DE,
∴DE=AE=3.
8. (1)解:根据小红同学设计,完成作图过程如解图所示;
第8题解图
(2)证明:在菱形ABCD中,∠ADE=∠CDE,AD=DC,
∵DE=DE,
∴△ADE≌△CDE(SAS),
∴AE=EC,
∵MN垂直平分AD,
∴AE=DE,
∴AE=DE=EC;
(3)解:∵在菱形ABCD中,∠ABC=72°,
∴∠ABD=∠DBC=36°,
∵AD∥BC,
∴∠ADB=∠DBC=36°,∠DAB=180°-∠ABC=108°.
∵AE=DE,
∴∠EAD=∠ADB=36°,
∴∠EAD=∠ABD=36°,
∵∠ADE=∠BDA,
∴△ADE∽△BDA,
∴=,即AD2=BD·DE.
∵∠BAE=∠BAD-∠EAD=72°,∠BEA=∠EAD+∠ADE=72°,
∴∠BAE=∠BEA,
∴BE=AB.
设AB=x=BE,DE=a(其中x,a>0),
则x2=(x+a)·a,
∴x2-ax-a2=0,解得x=a或x=a(舍去),
∴=,
设点A到BD距离为h,则点C到BD的距离为h,
∴S△AED=DE·h,
S△EDC=DE·h,
∴S△AED=S△EDC,
∴====.
同课章节目录
