2025年中考数学总复习44 微专题 反比例函数综合题 学案(含答案)
文档属性
| 名称 | 2025年中考数学总复习44 微专题 反比例函数综合题 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 150.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 00:00:00 | ||
图片预览




文档简介
微专题44 反比例函数综合题
1. 如图,已知点A(1,m)、B(n,1)在反比例函数y=(x>0)的图象上,过点A的一次函数y=kx+b的图象与y轴交于点C(0,1).
(1)求m、n的值和一次函数的表达式;
(2)连接AB,求点C到线段AB的距离.
第1题图
2. 如图,已知一次函数y1=x-3的图象与反比例函数y2=的图象相交于点A(4,n),与x轴相交于点B.
(1)求n和k的值;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE,BE,求△ABE的面积.
第2题图
3. 如图,点A是第一象限内直线y=2x上一点,过点A作AB⊥x轴于点B(a,0)(a>0),将△ABO绕点A逆时针旋转90°得到△ACD,点B的对应点C恰好落在反比例函数y=(k≠0,x>0)的图象上.
(1)若AO=2,求k的值;
(2)设直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点P,且点P横坐标为m.求证:为定值.
第3题图
4. 如图,一次函数y=-x+2的图象交x轴于点A,交y轴于点B,C为AB的中点,双曲线的一支y=(x>0)过点C,连接OC,将线段OC沿着y轴向上平移至EF,线段EF交y=(x>0)的图象于点D.
(1)求该反比例函数的表达式;
(2)若DE∶DF=1∶2,求点D的坐标.
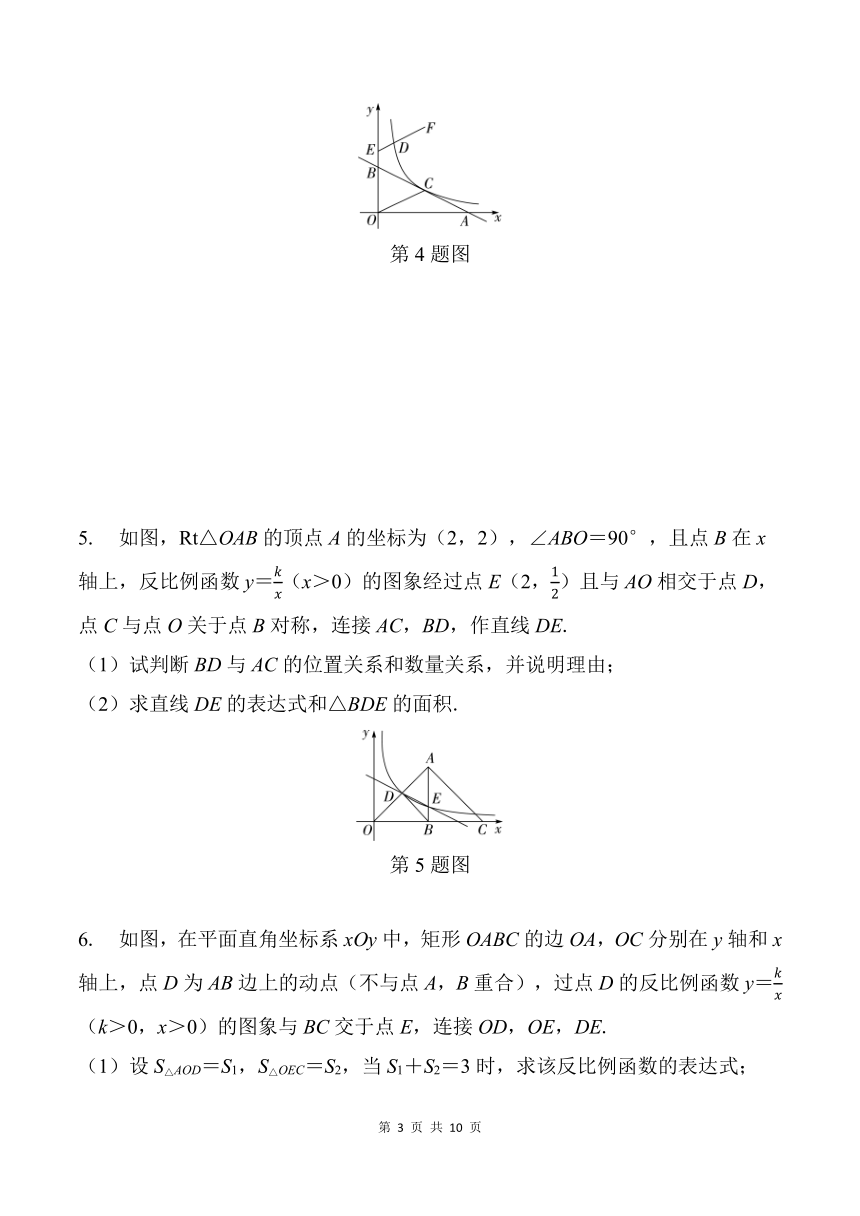
第4题图
5. 如图,Rt△OAB的顶点A的坐标为(2,2),∠ABO=90°,且点B在x轴上,反比例函数y=(x>0)的图象经过点E(2,)且与AO相交于点D,点C与点O关于点B对称,连接AC,BD,作直线DE.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)求直线DE的表达式和△BDE的面积.
第5题图
6. 如图,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别在y轴和x轴上,点D为AB边上的动点(不与点A,B重合),过点D的反比例函数y=(k>0,x>0)的图象与BC交于点E,连接OD,OE,DE.
(1)设S△AOD=S1,S△OEC=S2,当S1+S2=3时,求该反比例函数的表达式;
(2)若OA=6,AB=8,记S=S△ODE-S△BDE,求出S的最大值;
(3)在(2)的条件下,是否存在点D,使得△BDE沿直线DE折叠后点B的对应点B'恰好落在OC边上?若存在,求出点D的坐标;若不存在,请说明理由.
第6题图 备用图
1. 解:(1)∵点A(1,m),B(n,1)在反比例函数y=的图象上,
∴m=3,n=3.
又∵一次函数y=kx+b的图象过点A(1,3),C(0,1),
∴解得
∴一次函数的表达式为y=2x+1;
(2)如解图,连接BC,过点A作AD⊥BC,垂足为D,过点C作CE⊥AB,垂足为E.
∵C(0,1),B(3,1),
∴BC∥x轴,BC=3.
∵点A(1,3),B(3,1),AD⊥BC于点D,
∴点D(1,1),AD=2,DB=2.
在Rt△ADB中,AB==2.
又∵S△ABC=BC·AD=AB·CE,
即×3×2=×2·CE,
∴CE=,即点C到线段AB的距离为.
第1题解图
2. 解:(1)把A点坐标代入y1=x-3中,得n=×4-3=3,
∴A(4,3),
∵A点在反比例函数图象上,
∴k=3×4=12;
(2)如解图,过点A作AH⊥BC,垂足为H,连接AC,
∵A(4,3),∴AH=3,
当y1=0时,得x-3=0,
解得x=2,
∴点B的坐标为(2,0),
∴AB==,
∵四边形ABCD是菱形,
∴AB=BC=,AB∥CD,
∴S△ABE=S△ABC=BC·AH=××3=.
第2题解图
3. (1)解:∵AB⊥x轴于点B(a,0),点A是直线y=2x上一点,
∴A(a,2a),
∴OB=a,AB=2a,
在Rt△ABO中,
∵AO=2,AB2+OB2=AO2,
∴(2a)2+a2=(2)2,
解得a=2(负值已舍去),
∴AB=4,BO=2,
根据旋转的性质,得AC=AB=4,∠ACD=∠ABO=90°,
∴C(6,4),
∵点C在反比例函数y=图象上,
∴k=6×4=24;
(2)证明:由旋转可得OB=CD=a,由(1)知A(a,2a),
∴AC=AB=2a,
∴点C的坐标为(3a,2a),
∴k=2a·3a=6a2.
∵直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点P,点P的横坐标为m,
∴2m=,即=3.
由题意得,点P在第一象限内,
∴m>0且a>0,
∴=,
∴为定值.
4. 解:(1)在一次函数y=-x+2中,当x=0时,y=2,当y=0时,x=4,
∴一次函数y=-x+2的图象交x轴于点A(4,0),交y轴于点B(0,2),
∵C为AB的中点,
∴点C(2,1),
∵点C(2,1)在反比例函数y=(x>0)的图象上,
∴k=2×1=2,
∴反比例函数的表达式为y=;
(2)如解图,连接FC,过点D作x轴的平行线与FC交于点N,与y轴交于点M,
由题意可得FC∥y轴,
∴△EMD∽△FND,
∴==,
∴MD=MN=×2=,
即点D的横坐标为,
∵点D在反比例函数图象上,
∴当x=时,y==3,
∴点D(,3).
第4题解图
5. 解:(1)BD∥AC,BD=AC.理由如下:
∵反比例函数y=的图象经过点E(2,),
∴k=2×=1,
∴反比例函数的表达式为y=.
又∵点A的坐标为(2,2),
∴OA所在直线表达式为y=x,令y=,解得x=1或x=-1(舍去),
∴D(1,1),
∴点D为OA的中点,
∵点C与点O关于点B对称,
∴点B为OC的中点,即BD为△AOC的中位线,
∴BD∥AC,BD=AC;
(2)设直线DE的表达式为y=ax+b(a≠0),
将D(1,1),E(2,)分别代入,
得,解得,
∴直线DE的表达式为y=-x+.
∵点A的坐标为(2,2),∠ABO=90°,点B在x轴上,
∴点B的坐标为(2,0),
∴BE=,
∴S△BDE=BE×(|xE|-|xD|)=××(2-1)=.
6. 解:(1)∵点D,E在反比例函数y=(k>0,x>0)的图象上,
∴设D(x1,),E(x2,),x1>0,x2>0,x2>x1,
∴S1=x1·=,S2=x2·=.
∵S1+S2=3,
∴+=3,
∴k=3,
∴反比例函数的表达式为y=(x>0);
(2)由题意得,D(,6),E(8,),
∴S△BDE=BD·BE=(8-k)(6-k),
∴S△ODE=S矩形OABC-S△AOD-S△COE-S△BDE=6×8-k-k-S△BDE=48-k-S△BDE,
∴S=S△ODE-S△BDE=48-k-2S△BDE=48-k-2×(8-k)(6-k),
∴S=-k2+k.
∵-<0,
∴当k=-=24时,S有最大值,最大值为-×242+24=12;
(3)存在.如解图,过点D作DF⊥OC于点F.
由题意得,DF=AO=6,DB=DB'=8-k,B'E=BE=6-k,∠DB'E=∠B=∠C=90°,
∴∠DB'F+∠EB'C=∠EB'C+∠B'EC=90°,
∴∠DB'F=∠B'EC.
又∵∠DFB'=∠B'CE=90°,
∴△DFB'∽△B'CE,
∴=,
∴==,
∴B'C=.
∵B'C2+CE2=B'E2,
∴()2+()2=(6-k)2,解得k=,
∴DB'=DB=8-=,
∴AD=AB-DB=,
∴存在符合条件的点D,点D的坐标为(,6).
第6题解图
1. 如图,已知点A(1,m)、B(n,1)在反比例函数y=(x>0)的图象上,过点A的一次函数y=kx+b的图象与y轴交于点C(0,1).
(1)求m、n的值和一次函数的表达式;
(2)连接AB,求点C到线段AB的距离.
第1题图
2. 如图,已知一次函数y1=x-3的图象与反比例函数y2=的图象相交于点A(4,n),与x轴相交于点B.
(1)求n和k的值;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE,BE,求△ABE的面积.
第2题图
3. 如图,点A是第一象限内直线y=2x上一点,过点A作AB⊥x轴于点B(a,0)(a>0),将△ABO绕点A逆时针旋转90°得到△ACD,点B的对应点C恰好落在反比例函数y=(k≠0,x>0)的图象上.
(1)若AO=2,求k的值;
(2)设直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点P,且点P横坐标为m.求证:为定值.
第3题图
4. 如图,一次函数y=-x+2的图象交x轴于点A,交y轴于点B,C为AB的中点,双曲线的一支y=(x>0)过点C,连接OC,将线段OC沿着y轴向上平移至EF,线段EF交y=(x>0)的图象于点D.
(1)求该反比例函数的表达式;
(2)若DE∶DF=1∶2,求点D的坐标.
第4题图
5. 如图,Rt△OAB的顶点A的坐标为(2,2),∠ABO=90°,且点B在x轴上,反比例函数y=(x>0)的图象经过点E(2,)且与AO相交于点D,点C与点O关于点B对称,连接AC,BD,作直线DE.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)求直线DE的表达式和△BDE的面积.
第5题图
6. 如图,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别在y轴和x轴上,点D为AB边上的动点(不与点A,B重合),过点D的反比例函数y=(k>0,x>0)的图象与BC交于点E,连接OD,OE,DE.
(1)设S△AOD=S1,S△OEC=S2,当S1+S2=3时,求该反比例函数的表达式;
(2)若OA=6,AB=8,记S=S△ODE-S△BDE,求出S的最大值;
(3)在(2)的条件下,是否存在点D,使得△BDE沿直线DE折叠后点B的对应点B'恰好落在OC边上?若存在,求出点D的坐标;若不存在,请说明理由.
第6题图 备用图
1. 解:(1)∵点A(1,m),B(n,1)在反比例函数y=的图象上,
∴m=3,n=3.
又∵一次函数y=kx+b的图象过点A(1,3),C(0,1),
∴解得
∴一次函数的表达式为y=2x+1;
(2)如解图,连接BC,过点A作AD⊥BC,垂足为D,过点C作CE⊥AB,垂足为E.
∵C(0,1),B(3,1),
∴BC∥x轴,BC=3.
∵点A(1,3),B(3,1),AD⊥BC于点D,
∴点D(1,1),AD=2,DB=2.
在Rt△ADB中,AB==2.
又∵S△ABC=BC·AD=AB·CE,
即×3×2=×2·CE,
∴CE=,即点C到线段AB的距离为.
第1题解图
2. 解:(1)把A点坐标代入y1=x-3中,得n=×4-3=3,
∴A(4,3),
∵A点在反比例函数图象上,
∴k=3×4=12;
(2)如解图,过点A作AH⊥BC,垂足为H,连接AC,
∵A(4,3),∴AH=3,
当y1=0时,得x-3=0,
解得x=2,
∴点B的坐标为(2,0),
∴AB==,
∵四边形ABCD是菱形,
∴AB=BC=,AB∥CD,
∴S△ABE=S△ABC=BC·AH=××3=.
第2题解图
3. (1)解:∵AB⊥x轴于点B(a,0),点A是直线y=2x上一点,
∴A(a,2a),
∴OB=a,AB=2a,
在Rt△ABO中,
∵AO=2,AB2+OB2=AO2,
∴(2a)2+a2=(2)2,
解得a=2(负值已舍去),
∴AB=4,BO=2,
根据旋转的性质,得AC=AB=4,∠ACD=∠ABO=90°,
∴C(6,4),
∵点C在反比例函数y=图象上,
∴k=6×4=24;
(2)证明:由旋转可得OB=CD=a,由(1)知A(a,2a),
∴AC=AB=2a,
∴点C的坐标为(3a,2a),
∴k=2a·3a=6a2.
∵直线y=2x与反比例函数y=(k≠0,x>0)的图象交于点P,点P的横坐标为m,
∴2m=,即=3.
由题意得,点P在第一象限内,
∴m>0且a>0,
∴=,
∴为定值.
4. 解:(1)在一次函数y=-x+2中,当x=0时,y=2,当y=0时,x=4,
∴一次函数y=-x+2的图象交x轴于点A(4,0),交y轴于点B(0,2),
∵C为AB的中点,
∴点C(2,1),
∵点C(2,1)在反比例函数y=(x>0)的图象上,
∴k=2×1=2,
∴反比例函数的表达式为y=;
(2)如解图,连接FC,过点D作x轴的平行线与FC交于点N,与y轴交于点M,
由题意可得FC∥y轴,
∴△EMD∽△FND,
∴==,
∴MD=MN=×2=,
即点D的横坐标为,
∵点D在反比例函数图象上,
∴当x=时,y==3,
∴点D(,3).
第4题解图
5. 解:(1)BD∥AC,BD=AC.理由如下:
∵反比例函数y=的图象经过点E(2,),
∴k=2×=1,
∴反比例函数的表达式为y=.
又∵点A的坐标为(2,2),
∴OA所在直线表达式为y=x,令y=,解得x=1或x=-1(舍去),
∴D(1,1),
∴点D为OA的中点,
∵点C与点O关于点B对称,
∴点B为OC的中点,即BD为△AOC的中位线,
∴BD∥AC,BD=AC;
(2)设直线DE的表达式为y=ax+b(a≠0),
将D(1,1),E(2,)分别代入,
得,解得,
∴直线DE的表达式为y=-x+.
∵点A的坐标为(2,2),∠ABO=90°,点B在x轴上,
∴点B的坐标为(2,0),
∴BE=,
∴S△BDE=BE×(|xE|-|xD|)=××(2-1)=.
6. 解:(1)∵点D,E在反比例函数y=(k>0,x>0)的图象上,
∴设D(x1,),E(x2,),x1>0,x2>0,x2>x1,
∴S1=x1·=,S2=x2·=.
∵S1+S2=3,
∴+=3,
∴k=3,
∴反比例函数的表达式为y=(x>0);
(2)由题意得,D(,6),E(8,),
∴S△BDE=BD·BE=(8-k)(6-k),
∴S△ODE=S矩形OABC-S△AOD-S△COE-S△BDE=6×8-k-k-S△BDE=48-k-S△BDE,
∴S=S△ODE-S△BDE=48-k-2S△BDE=48-k-2×(8-k)(6-k),
∴S=-k2+k.
∵-<0,
∴当k=-=24时,S有最大值,最大值为-×242+24=12;
(3)存在.如解图,过点D作DF⊥OC于点F.
由题意得,DF=AO=6,DB=DB'=8-k,B'E=BE=6-k,∠DB'E=∠B=∠C=90°,
∴∠DB'F+∠EB'C=∠EB'C+∠B'EC=90°,
∴∠DB'F=∠B'EC.
又∵∠DFB'=∠B'CE=90°,
∴△DFB'∽△B'CE,
∴=,
∴==,
∴B'C=.
∵B'C2+CE2=B'E2,
∴()2+()2=(6-k)2,解得k=,
∴DB'=DB=8-=,
∴AD=AB-DB=,
∴存在符合条件的点D,点D的坐标为(,6).
第6题解图
同课章节目录
