2025年中考数学总复习46 微专题 几何综合题 学案(含答案)
文档属性
| 名称 | 2025年中考数学总复习46 微专题 几何综合题 学案(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 428.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 19:44:01 | ||
图片预览


文档简介
微专题46 几何综合题
类型一 动点型探究
1. 综合探究
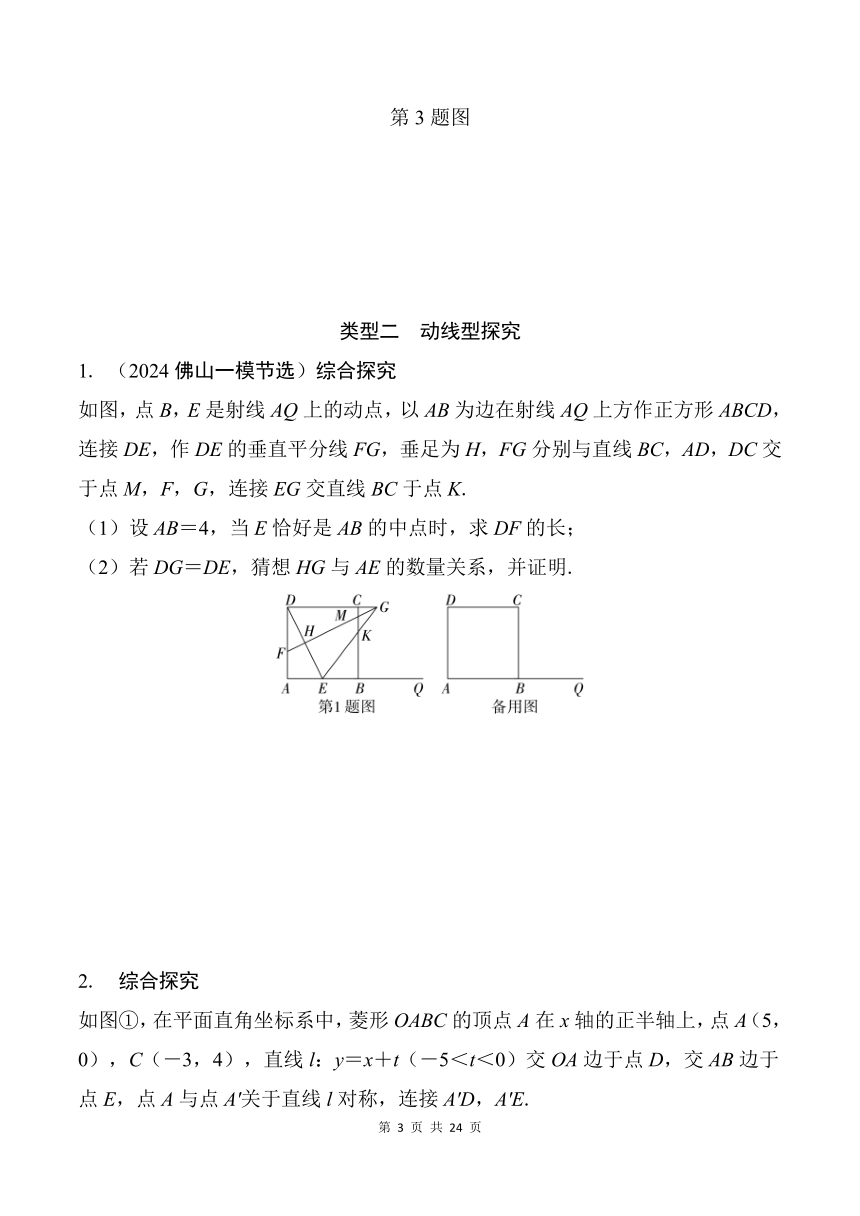
已知点E是边长为2的正方形ABCD内部一个动点,始终保持∠AED=90°.
【初步探究】
(1)如图①,延长DE交边BC于点F.当点F是BC的中点时,求的值;
【深入探究】
(2)如图②,连接CE并延长交边AD于点M.当点M是AD的中点时,求的值.
第1题图
2.综合运用
如图,在平面直角坐标系中,矩形ABCD的顶点C在原点O处,已知点B(8,0),D(0,6),连接AC,E是CD上一动点(不与点C,D重合),过点E作EF∥AC交AD于点F,过点E作EG⊥EF交BC于点G,连接FG.
(1)若DE=CG,求证:△DEF≌△CGE;
(2)设DE=a,用含a的式子表示△EFG的面积,并求出△EFG面积的最大值.
第2题图
3. 已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如图①,连接BC.
(1)填空:∠OBC= °;
(2)如图①,连接AC,作OP⊥AC,垂足为P,求OP的长度;
(3)如图②,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒.设运动时间为x秒, △OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
第3题图
类型二 动线型探究
1. (2024佛山一模节选)综合探究
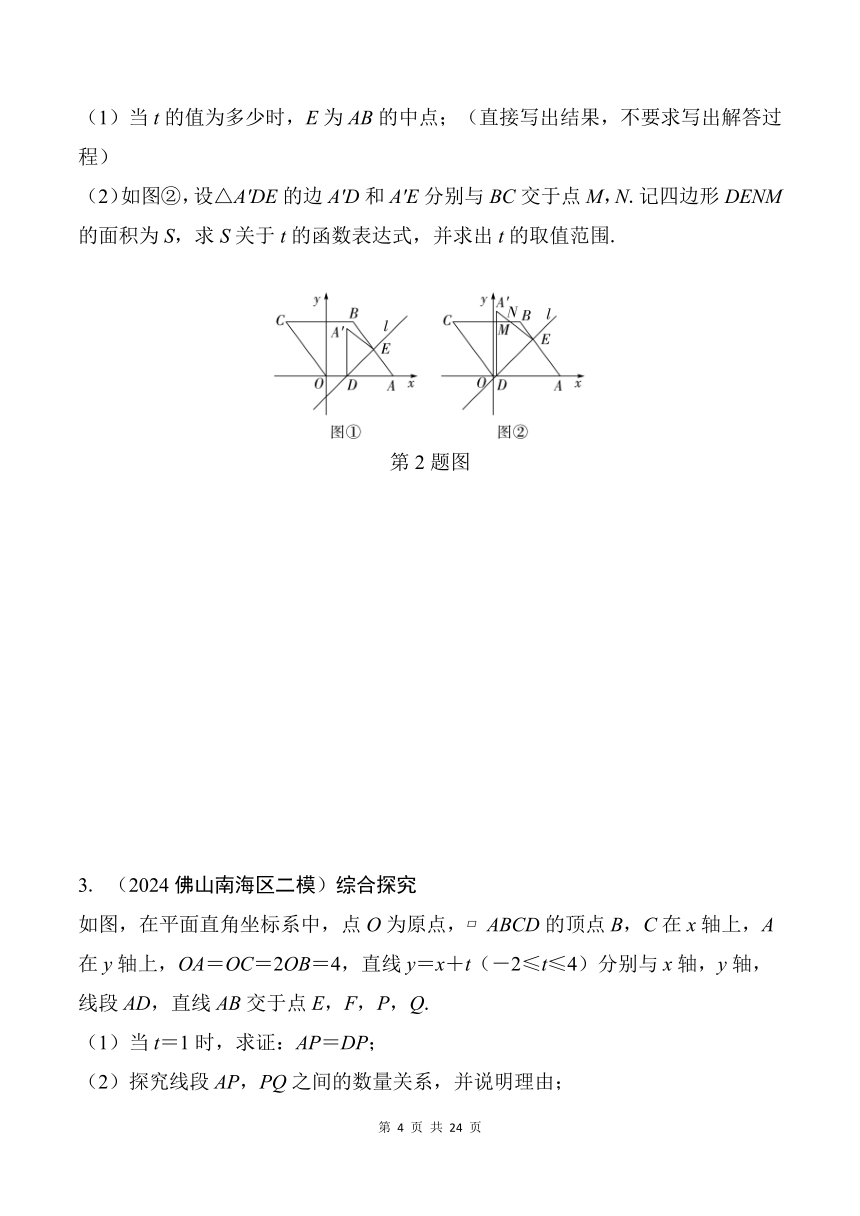
如图,点B,E是射线AQ上的动点,以AB为边在射线AQ上方作正方形ABCD,连接DE,作DE的垂直平分线FG,垂足为H,FG分别与直线BC,AD,DC交于点M,F,G,连接EG交直线BC于点K.
(1)设AB=4,当E恰好是AB的中点时,求DF的长;
(2)若DG=DE,猜想HG与AE的数量关系,并证明.
2. 综合探究
如图①,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,点A(5,0),C(-3,4),直线l:y=x+t(-5<t<0)交OA边于点D,交AB边于点E,点A与点A'关于直线l对称,连接A'D,A'E.
(1)当t的值为多少时,E为AB的中点;(直接写出结果,不要求写出解答过程)
(2)如图②,设△A'DE的边A'D和A'E分别与BC交于点M,N.记四边形DENM的面积为S,求S关于t的函数表达式,并求出t的取值范围.
第2题图
3. (2024佛山南海区二模)综合探究
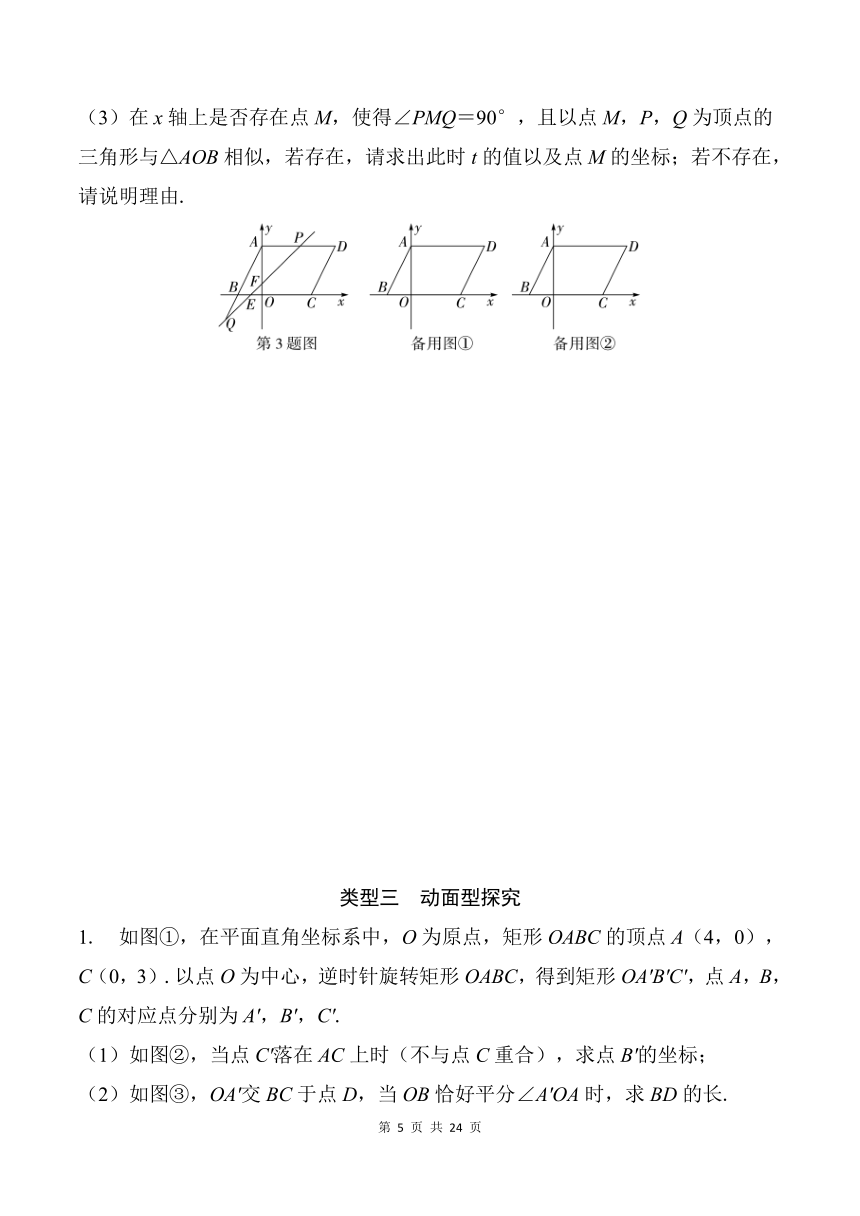
如图,在平面直角坐标系中,点O为原点, ABCD的顶点B,C在x轴上,A在y轴上,OA=OC=2OB=4,直线y=x+t(-2≤t≤4)分别与x轴,y轴,线段AD,直线AB交于点E,F,P,Q.
(1)当t=1时,求证:AP=DP;
(2)探究线段AP,PQ之间的数量关系,并说明理由;
(3)在x轴上是否存在点M,使得∠PMQ=90°,且以点M,P,Q为顶点的三角形与△AOB相似,若存在,请求出此时t的值以及点M的坐标;若不存在,请说明理由.
类型三 动面型探究
1. 如图①,在平面直角坐标系中,O为原点,矩形OABC的顶点A(4,0),C(0,3).以点O为中心,逆时针旋转矩形OABC,得到矩形OA'B'C',点A,B,C的对应点分别为A',B',C'.
(1)如图②,当点C'落在AC上时(不与点C重合),求点B'的坐标;
(2)如图③,OA'交BC于点D,当OB恰好平分∠A'OA时,求BD的长.
第1题图
2. 在平面直角坐标系中,O为坐标原点,菱形OABC的顶点A(4,0),C(2,2),矩形ODEF的顶点D(0,),F(-4,0).
(1)如图①,点E的坐标为 ,点B的坐标为 ;
(2)将矩形ODEF沿水平方向向右平移,得到矩形O'D'E'F',点O,D,E,F的对应点分别为O',D',E',F'.设OO'=t,矩形O'D'E'F'与菱形OABC重叠部分的面积为S.当边O'D'与AB相交于点G,边OC分别与D'E',E'F'相交于点H,M,且矩形O'D'E'F'与菱形OABC重叠部分为六边形时,试用含t的式子表示S,并直接写出t的取值范围.
第2题图
3. (2024广东22题13分)【知识技能】
(1)如图①,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A'DC'.当点E的对应点E'与点A重合时,求证:AB=BC.
【数学理解】
(2)如图②,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A'DC',连接A'B,C'C,作△A'BD的中线DF.求证:2DF·CD=BD·CC'.
【拓展探索】
(3)如图③,在△ABC中,tan B=,点D在AB上,AD=.过点D作DE⊥BC,垂足为E,BE=3,CE=.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
第3题图
类型一 动点型探究
1. 解:(1)如解图①,∵在正方形ABCD中,∠AED=∠ADC=∠C=90°,AB=BC=CD=AD=2,
∴∠2=90°-∠3=∠1,
∴tan∠2=tan∠1,
∴==.
∵F是BC的中点,
∴==;
第1题解图①
(2)如解图②,延长DE交边BC于点F,
∵M是AD的中点,∠AED=90°,
∴AM=MD=ME=AD=1,
∴∠2=∠1,
在Rt△MDC中,MC===,
∴CE=MC-ME=-1.
∵在正方形ABCD中,AD∥BC,
∴∠2=∠4,
∵∠1=∠3,
∴∠4=∠3,
∴CF=CE=-1,
与(1)同理可得,==.
第1题解图②
2. (1)证明:∵四边形ABCD是矩形,
∴∠ADC=∠DCB=90°,
∵EG⊥EF,∴∠FEG=90°,
∴∠CEG+∠FED=90°,
∵∠DFE+∠FED=90°,
∴∠DFE=∠CEG,
∵DE=CG,∠FDE=∠ECG,
∴△DEF≌△CGE(AAS);
(2)解:∵B(8,0),D(0,6),
∴CB=8,CD=6,
∵四边形ABCD是矩形,
∴AD=BC=8,
在Rt△ADC中,AC==10.
∵EF∥AC,
∴△DEF∽△DCA
∴=,即=,解得EF=a.
由(1)知∠DFE=∠CEG,
∵EF∥AC,
∴∠DFE=∠DAC,
∴∠CEG=∠DAC,
∵∠ECG=∠ADC,
∴△CEG∽△DAC,
∴=,即=,解得EG=(6-a),
∴S△EFG=EF·EG=×a×(6-a)=(6a-a2)=-(a-3)2+,
∵-<0,0<a<6,
∴当a=3时,△EFG的面积有最大值,最大值为.
3. 解:(1)60;
【解法提示】由旋转的性质可知,OB=OC,∠BOC=60°,∴△OBC是等边三角形,∴∠OBC=60°.
(2)在Rt△OAB中,OB=4,∠ABO=30°,
∴∠AOB=60°,OA=OB=2,AB=OB·cos 30°=2,
由旋转的性质可知,OB=OC,∠BOC=60°,
∴△OBC是等边三角形,
∴∠AOB=∠OBC=60°,BC=OB=4,
∴OA∥BC,AB即为△AOC的高,
∴S△AOC=AO·AB=×2×2=2,
∵∠ABC=∠ABO+∠OBC =90°,
∴AC===2,
∵OP⊥AC,
∴S△AOC=AC·OP,即×2·OP=2,
解得OP=;
一题多解法
由旋转的性质可知,OB=OC,
∠BOC=60°,
∴△OBC为等边三角形,
∴BC=OB=4,∠OBC=60°,
∵∠ABO=30°,
∴OA=OB=2,AB=OB=2,∠ABC=90°,
∴BC∥OA,AC==2,
∴∠PAO=∠ACB,
∵sin∠ACB==,
∴sin∠PAO=sin∠ACB=,
∴=,
∴OP=OA=;
(3)根据题意得,M运动到点C时,所需时间为=(秒),N运动到点B时,所需时间为=4(秒),当M,N相遇时,所需时间为=(秒),
∴分三种情况讨论:
①当0<x≤时,点M在OC上,点N在OB上,如解图①,过点N作NE⊥OC于点E,
则NE=ON·sin 60°=x,
∴y=OM·NE=×1.5x×x=x2,
∵>0,
∴当x=时,y最大=×()2=;
②当<x<4时,点M在BC上,点N在OB上,如解图②,
BM=8-x,过点M作MF⊥OB于点F,
∴MF=BM·sin 60°=(8-x),
∴y=ON·MF=x·(8-x)=2x-x2,
∵-<0,
∴当x=-=-=时,
y最大=2×-×()2=;
③当4≤x<时,点M,N都在BC上,如解图③,
MN=12-x,
过点O作OG⊥BC于点G,
则OG=AB=2,
∴y=MN·OG=(12-x)·2=-x+12,
∵-<0,
∴当x=4时,y最大=2.
综上所述,当x=时,y取得最大值,最大值为.
第3题解图
类型二 动线型探究
1. 解:(1)如解图①,连接EF,
在正方形ABCD中,AB=AD=4,
∵E是AB中点,
∴AE=EB=2,
∵F为线段DE垂直平分线上一点,
∴DF=EF,
设DF=x,则AF=4-x,
在Rt△AFE中,根据勾股定理得,(4-x)2+22=x2,
解得x=,∴DF=;
第1题解图①
(2)HG=AE.证明如下:
∵GF垂直平分DE,
∴DG=GE,∠DHG=90°,
∵DG=DE,
∴DG=DE=EG,
∴△DGE是等边三角形,
∴∠GDE=60°,
∵正方形ABCD中,∠CDA=∠DAB=90°,
∴∠ADE=∠DGH=30°,
∴AE=DE=DH,
∵∠DAE=∠DHG=90°,
∴△ADE≌△HGD,
∴AD=HG,
在Rt△ADE中,AD=AE,
∴HG=AE.
2. 解:(1)t=-时,E为AB的中点;
【解法提示】∵A(5,0),四边形OABC是菱形,∴OA=BC=5,OA∥BC.∵C(-3,4),∴B(2,4).∵E为AB中点,∴E(,2),将点E代入y=x+t中,得+t=2,解得t=-.
(2)如解图,记BC交y轴于点H,
∵四边形OABC为菱形,A(5,0),C(-3,4),
∴∠OAE=∠C,BC∥OA,OA=BC=5,CH=3,OH=4,
∴在Rt△COH中,tan C==,
由对称的性质,得A'D=AD,∠A'=∠OAE=∠C,∠ADE=∠A'DE,∴tan A'=.
由题意可知,∠ADE=45°,
∴∠A'DE=∠ADE=45°,
∴∠A'DA=90°,
∴∠A'MN=90°,DM=OH=4.
在y=x+t中,令y=0,得x+t=0,解得x=-t,∴OD=-t,AD=5+t.
∵DM=4,tan A'=,
∴A'M=A'D-DM=AD-DM=1+t,
∴在Rt△A'MN中,MN=A'M·tan A'=(1+t),
∴S△A'MN=A'M·MN=(1+t)2.
如解图,过点E作EK⊥OA于点K,
设DK=x,则AK=5+t-x.
∵∠EDK=45°,∠EKD=90°,
∴EK=DK=x,
在Rt△AEK中,∵tan A==,∴=,解得x=,
∴S△A'DE=S△ADE=AD·EK=×(5+t)×=(5+t)2,
∴S=S△A'DE-S△A'MN=(5+t)2-(1+t)2=-t2+t+.
∵A'D>DM,∴5+t>4,∴t>-1,
又∵-5<t<0,
∴t的取值范围为-1<t<0.
第2题解图
3. (1)证明:由OA=OC=2OB=4知,OC=4,OB=2,
又∵四边形ABCD为平行四边形,
∴AD=BC=6,
则点A,B的坐标分别为(0,4),(-2,0),
当y=4时,y=x+t=4,
则x=4-t=4-1=3=AD,
即点P(3,4),
∴AP=DP;
(2)解:PQ=2AP,理由:
由点A,B的坐标,得直线AB的表达式为y=2x+4,
联立上式和y=x+t得2x+4=x+t,
解得x=t-4,
即点Q(t-4,2t-4),
在直线y=x+t中,当y=4时,x=4-t,
∴点P(4-t,4),
则AP=4-t,
由点P,Q的坐标,得PQ=2(4-t)=2AP;
(3)解:存在.如解图①②③,过点P作PH⊥x轴于点H,过点Q作QI⊥x轴于点I,
设点M(m,0),
由(2)知,点P,Q的坐标分别为(4-t,4),(t-4,2t-4),
则HM=|m-4+t|,PH=OA=4,IM=|m-t+4|,QI=|4-2t|,
∵∠PMH+∠QMI=90°,∠QMI+∠IQM=90°,
∴∠IQM=∠PMH,
又∵∠PHM=∠MIQ=90°,
∴△PHM∽△MIQ,
∵以点M,P,Q为顶点的三角形与△AOB相似,
则PM∶QM=2或,
∴Rt△PHM和Rt△MIQ的相似比为2或,
则PH∶MI=HM∶IQ=2或,
当m>0时,如解图①②,
当相似比为2时,如解图①,
==2,
则PH=2MI,MH=2QI,
即4=2(m-t+4)且4-t-m=2(2t-4),
第3题解图①
解得m=,t=,
即点M(,0),t=;
当相似比为时,如解图②,
==,
则PH=MI,MH=QI,
第3题解图②
则2×4=m-(t-4)且2(m-4+t)=4-2t,
解得m=,t=,
则点M(,0),t=;
当m<0时,如解图③,
第3题解图③
当相似比为2时,如解图③,
==2,
则PH=2MI,MH=2QI,
则4=2[(t-4)-m]且4-t-m=2(4-2t),
解得m=-7,t=-1,
即点M(-7,0),t=-1;
当相似比为时,
经验证,该情况不存在,
综上所述,点M(,0),t=或M(,0),t=或M(-7,0),t=-1.
类型三 动面型探究
1. 解:(1)如解图,连接OB',AB',
∵A(4,0),C(0,3),
∴OA=4,OC=3,
由旋转的性质,得C'O=CO=3,OA'=OA=4,
∴∠OCA=∠OC'C,
∵tan∠OCA==,
tan∠B'OC'==,
∴∠OCA=∠B'OC',
∴∠OC'C=∠B'OC',
∴AC∥OB',
∵四边形ABCO为矩形,
∴AC=OB',
∴四边形OCAB'是平行四边形,
∴AB'=OC=3,AB'∥OC,即AB'∥y轴,
∴点B'的坐标为(4,-3);
第1题解图
(2)∵OB平分∠A'OA,
∴∠DOB=∠AOB,
∵BC∥OA,
∴∠DBO=∠AOB,
∴∠DOB=∠DBO,
∴BD=OD,
设CD=x,则BD=BC-CD=4-x,
∴OD=4-x,
在Rt△OCD中,由勾股定理,得OD2=CD2+OC2,
∴(4-x)2=x2+32,解得x=,
∴BD=4-x=.
2. 解:(1)(-4,),(6,2);
【解法提示】∵四边形ODEF为矩形,D(0,),F(-4,0),∴E(-4,),∵四边形OABC为菱形,A(4,0),∴BC=OA=4,∵C(2,2),∴B(6,2).
(2)如解图,过点C作CN⊥OA于点N,
∵C(2,2),
∴ON=2,CN=2,
∴tan∠CON===,
∴∠CON=60°,
过点H作HR⊥x轴于点R,
∵E'F'=,
∴HR=E'F'=,
∵∠COA=60°,
∴OR===1,
∴H(1,),
由平移可知OO'=EE'=t,
∵E(-4,),
∴E'(-4+t,),
∴E'H=1-(-4+t)=5-t,
∵∠E'HO=∠HOF'=60°,
∴E'M=E'H·tan60°=(5-t),
∵在Rt△AGO'中,AO'=OO'-OA=t-4,∠GAO'=∠COA=60°,
∴GO'=AO'·tan 60°=(t-4),
∴S=S矩形O'D'E'F'-S△MHE'-S△AGO'=4-×(5-t)2-×(t-4)2=-t2+9t-,其中t的取值范围是4<t<5.
第2题解图
3. (1)证明:∵DE是△ABC的中位线,
∴DE=BC,AD=AB,
由旋转性质得AD=DE,
∴AB=BC; (3分)
(2)证明:如解图①,连接AA',
∵DE是△ABC的中位线,F为A'B的中点,
∴DA=BD,
∴DF是△ABA'的中位线,
∴2DF=AA',
由旋转性质得△A'DC'≌△ADC,∠A'DA=∠C'DC,A'D=AD,C'D=CD,
∴=,
∴△A'DA∽△C'DC,
∴=,
∴=,
∴2DF·CD=BD·CC'; (7分)
第3题解图①
(3)解:存在点G,使得∠AGD+∠CGE=180°,证明如下:
如解图②,过点D作DF∥BC交AC于点F,过点C作CH⊥AB于点H,DF与CH交于点G,连接EG,AG,
∵DE⊥BC,
∴∠DEB=90°,
在Rt△BDE中,tan B=,BE=3,
∴DE=4,BD=5,cos B=,sin B=, (8分)
在Rt△BCH中,cos B==,BC=BE+CE=3+=,
∴BH=,
∴AH=AD+BD-BH=+5-=,
∴DH=AD-AH=-==AH, (9分)
∵CH⊥AD,
∴△ADG为等腰三角形,
∴∠AGH=∠DGH, (10分)
∵DF∥BC,
∴∠ADG=∠B,∠EDG=90°,
∴tan∠ADG=tan B=,
cos∠ADG=cos B=,
∴=,=,
∵DH=,
∴HG=,DG=, (11分)
∵=,=,
∴=,
∵∠DHG=∠EDG=90°,
∴△DHG∽△EDG,
∴∠DGH=∠EGD, (12分)
∴∠DGE=∠AGH,
∵∠AGC+∠AGH=180°,
∴∠AGC+∠DGE=180°,
∴∠AGD+∠CGE=180°. (13分)
第3题解图②
一题多解法
如解图③,取AD中点M,CE中点N,连接MN,
∵AD是☉M直径,CE是☉N直径,
∴∠AGD=90°,∠CGE=90°,
∴∠AGD+∠CGE=180°,
∵tan B=,BE=3,
∴BD=5,
∵CE=,
∴EN=CE=,
∴BN=BE+EN=,
∵DE⊥CE,
∴DE是☉N的切线,即DE在☉N外,
作NF⊥AB,
∵∠B=∠B,∠BED=∠BFN=90°,
∴△BDE∽△BNF,
∴=,
∴NF=>,即NF>rn,
∴AB在☉N外,
∴G点在四边形ADEC内部.
作MH⊥BC,
∵BM=,tan B=,
∴BH=,MH=,
∴NH=,
∴MN=≈7.4<AM+CN,
∴☉M和☉N有交点.
第3题解图③
类型一 动点型探究
1. 综合探究
已知点E是边长为2的正方形ABCD内部一个动点,始终保持∠AED=90°.
【初步探究】
(1)如图①,延长DE交边BC于点F.当点F是BC的中点时,求的值;
【深入探究】
(2)如图②,连接CE并延长交边AD于点M.当点M是AD的中点时,求的值.
第1题图
2.综合运用
如图,在平面直角坐标系中,矩形ABCD的顶点C在原点O处,已知点B(8,0),D(0,6),连接AC,E是CD上一动点(不与点C,D重合),过点E作EF∥AC交AD于点F,过点E作EG⊥EF交BC于点G,连接FG.
(1)若DE=CG,求证:△DEF≌△CGE;
(2)设DE=a,用含a的式子表示△EFG的面积,并求出△EFG面积的最大值.
第2题图
3. 已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O顺时针旋转60°,如图①,连接BC.
(1)填空:∠OBC= °;
(2)如图①,连接AC,作OP⊥AC,垂足为P,求OP的长度;
(3)如图②,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒.设运动时间为x秒, △OMN的面积为y,求当x为何值时y取得最大值?最大值为多少?
第3题图
类型二 动线型探究
1. (2024佛山一模节选)综合探究
如图,点B,E是射线AQ上的动点,以AB为边在射线AQ上方作正方形ABCD,连接DE,作DE的垂直平分线FG,垂足为H,FG分别与直线BC,AD,DC交于点M,F,G,连接EG交直线BC于点K.
(1)设AB=4,当E恰好是AB的中点时,求DF的长;
(2)若DG=DE,猜想HG与AE的数量关系,并证明.
2. 综合探究
如图①,在平面直角坐标系中,菱形OABC的顶点A在x轴的正半轴上,点A(5,0),C(-3,4),直线l:y=x+t(-5<t<0)交OA边于点D,交AB边于点E,点A与点A'关于直线l对称,连接A'D,A'E.
(1)当t的值为多少时,E为AB的中点;(直接写出结果,不要求写出解答过程)
(2)如图②,设△A'DE的边A'D和A'E分别与BC交于点M,N.记四边形DENM的面积为S,求S关于t的函数表达式,并求出t的取值范围.
第2题图
3. (2024佛山南海区二模)综合探究
如图,在平面直角坐标系中,点O为原点, ABCD的顶点B,C在x轴上,A在y轴上,OA=OC=2OB=4,直线y=x+t(-2≤t≤4)分别与x轴,y轴,线段AD,直线AB交于点E,F,P,Q.
(1)当t=1时,求证:AP=DP;
(2)探究线段AP,PQ之间的数量关系,并说明理由;
(3)在x轴上是否存在点M,使得∠PMQ=90°,且以点M,P,Q为顶点的三角形与△AOB相似,若存在,请求出此时t的值以及点M的坐标;若不存在,请说明理由.
类型三 动面型探究
1. 如图①,在平面直角坐标系中,O为原点,矩形OABC的顶点A(4,0),C(0,3).以点O为中心,逆时针旋转矩形OABC,得到矩形OA'B'C',点A,B,C的对应点分别为A',B',C'.
(1)如图②,当点C'落在AC上时(不与点C重合),求点B'的坐标;
(2)如图③,OA'交BC于点D,当OB恰好平分∠A'OA时,求BD的长.
第1题图
2. 在平面直角坐标系中,O为坐标原点,菱形OABC的顶点A(4,0),C(2,2),矩形ODEF的顶点D(0,),F(-4,0).
(1)如图①,点E的坐标为 ,点B的坐标为 ;
(2)将矩形ODEF沿水平方向向右平移,得到矩形O'D'E'F',点O,D,E,F的对应点分别为O',D',E',F'.设OO'=t,矩形O'D'E'F'与菱形OABC重叠部分的面积为S.当边O'D'与AB相交于点G,边OC分别与D'E',E'F'相交于点H,M,且矩形O'D'E'F'与菱形OABC重叠部分为六边形时,试用含t的式子表示S,并直接写出t的取值范围.
第2题图
3. (2024广东22题13分)【知识技能】
(1)如图①,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A'DC'.当点E的对应点E'与点A重合时,求证:AB=BC.
【数学理解】
(2)如图②,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A'DC',连接A'B,C'C,作△A'BD的中线DF.求证:2DF·CD=BD·CC'.
【拓展探索】
(3)如图③,在△ABC中,tan B=,点D在AB上,AD=.过点D作DE⊥BC,垂足为E,BE=3,CE=.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
第3题图
类型一 动点型探究
1. 解:(1)如解图①,∵在正方形ABCD中,∠AED=∠ADC=∠C=90°,AB=BC=CD=AD=2,
∴∠2=90°-∠3=∠1,
∴tan∠2=tan∠1,
∴==.
∵F是BC的中点,
∴==;
第1题解图①
(2)如解图②,延长DE交边BC于点F,
∵M是AD的中点,∠AED=90°,
∴AM=MD=ME=AD=1,
∴∠2=∠1,
在Rt△MDC中,MC===,
∴CE=MC-ME=-1.
∵在正方形ABCD中,AD∥BC,
∴∠2=∠4,
∵∠1=∠3,
∴∠4=∠3,
∴CF=CE=-1,
与(1)同理可得,==.
第1题解图②
2. (1)证明:∵四边形ABCD是矩形,
∴∠ADC=∠DCB=90°,
∵EG⊥EF,∴∠FEG=90°,
∴∠CEG+∠FED=90°,
∵∠DFE+∠FED=90°,
∴∠DFE=∠CEG,
∵DE=CG,∠FDE=∠ECG,
∴△DEF≌△CGE(AAS);
(2)解:∵B(8,0),D(0,6),
∴CB=8,CD=6,
∵四边形ABCD是矩形,
∴AD=BC=8,
在Rt△ADC中,AC==10.
∵EF∥AC,
∴△DEF∽△DCA
∴=,即=,解得EF=a.
由(1)知∠DFE=∠CEG,
∵EF∥AC,
∴∠DFE=∠DAC,
∴∠CEG=∠DAC,
∵∠ECG=∠ADC,
∴△CEG∽△DAC,
∴=,即=,解得EG=(6-a),
∴S△EFG=EF·EG=×a×(6-a)=(6a-a2)=-(a-3)2+,
∵-<0,0<a<6,
∴当a=3时,△EFG的面积有最大值,最大值为.
3. 解:(1)60;
【解法提示】由旋转的性质可知,OB=OC,∠BOC=60°,∴△OBC是等边三角形,∴∠OBC=60°.
(2)在Rt△OAB中,OB=4,∠ABO=30°,
∴∠AOB=60°,OA=OB=2,AB=OB·cos 30°=2,
由旋转的性质可知,OB=OC,∠BOC=60°,
∴△OBC是等边三角形,
∴∠AOB=∠OBC=60°,BC=OB=4,
∴OA∥BC,AB即为△AOC的高,
∴S△AOC=AO·AB=×2×2=2,
∵∠ABC=∠ABO+∠OBC =90°,
∴AC===2,
∵OP⊥AC,
∴S△AOC=AC·OP,即×2·OP=2,
解得OP=;
一题多解法
由旋转的性质可知,OB=OC,
∠BOC=60°,
∴△OBC为等边三角形,
∴BC=OB=4,∠OBC=60°,
∵∠ABO=30°,
∴OA=OB=2,AB=OB=2,∠ABC=90°,
∴BC∥OA,AC==2,
∴∠PAO=∠ACB,
∵sin∠ACB==,
∴sin∠PAO=sin∠ACB=,
∴=,
∴OP=OA=;
(3)根据题意得,M运动到点C时,所需时间为=(秒),N运动到点B时,所需时间为=4(秒),当M,N相遇时,所需时间为=(秒),
∴分三种情况讨论:
①当0<x≤时,点M在OC上,点N在OB上,如解图①,过点N作NE⊥OC于点E,
则NE=ON·sin 60°=x,
∴y=OM·NE=×1.5x×x=x2,
∵>0,
∴当x=时,y最大=×()2=;
②当<x<4时,点M在BC上,点N在OB上,如解图②,
BM=8-x,过点M作MF⊥OB于点F,
∴MF=BM·sin 60°=(8-x),
∴y=ON·MF=x·(8-x)=2x-x2,
∵-<0,
∴当x=-=-=时,
y最大=2×-×()2=;
③当4≤x<时,点M,N都在BC上,如解图③,
MN=12-x,
过点O作OG⊥BC于点G,
则OG=AB=2,
∴y=MN·OG=(12-x)·2=-x+12,
∵-<0,
∴当x=4时,y最大=2.
综上所述,当x=时,y取得最大值,最大值为.
第3题解图
类型二 动线型探究
1. 解:(1)如解图①,连接EF,
在正方形ABCD中,AB=AD=4,
∵E是AB中点,
∴AE=EB=2,
∵F为线段DE垂直平分线上一点,
∴DF=EF,
设DF=x,则AF=4-x,
在Rt△AFE中,根据勾股定理得,(4-x)2+22=x2,
解得x=,∴DF=;
第1题解图①
(2)HG=AE.证明如下:
∵GF垂直平分DE,
∴DG=GE,∠DHG=90°,
∵DG=DE,
∴DG=DE=EG,
∴△DGE是等边三角形,
∴∠GDE=60°,
∵正方形ABCD中,∠CDA=∠DAB=90°,
∴∠ADE=∠DGH=30°,
∴AE=DE=DH,
∵∠DAE=∠DHG=90°,
∴△ADE≌△HGD,
∴AD=HG,
在Rt△ADE中,AD=AE,
∴HG=AE.
2. 解:(1)t=-时,E为AB的中点;
【解法提示】∵A(5,0),四边形OABC是菱形,∴OA=BC=5,OA∥BC.∵C(-3,4),∴B(2,4).∵E为AB中点,∴E(,2),将点E代入y=x+t中,得+t=2,解得t=-.
(2)如解图,记BC交y轴于点H,
∵四边形OABC为菱形,A(5,0),C(-3,4),
∴∠OAE=∠C,BC∥OA,OA=BC=5,CH=3,OH=4,
∴在Rt△COH中,tan C==,
由对称的性质,得A'D=AD,∠A'=∠OAE=∠C,∠ADE=∠A'DE,∴tan A'=.
由题意可知,∠ADE=45°,
∴∠A'DE=∠ADE=45°,
∴∠A'DA=90°,
∴∠A'MN=90°,DM=OH=4.
在y=x+t中,令y=0,得x+t=0,解得x=-t,∴OD=-t,AD=5+t.
∵DM=4,tan A'=,
∴A'M=A'D-DM=AD-DM=1+t,
∴在Rt△A'MN中,MN=A'M·tan A'=(1+t),
∴S△A'MN=A'M·MN=(1+t)2.
如解图,过点E作EK⊥OA于点K,
设DK=x,则AK=5+t-x.
∵∠EDK=45°,∠EKD=90°,
∴EK=DK=x,
在Rt△AEK中,∵tan A==,∴=,解得x=,
∴S△A'DE=S△ADE=AD·EK=×(5+t)×=(5+t)2,
∴S=S△A'DE-S△A'MN=(5+t)2-(1+t)2=-t2+t+.
∵A'D>DM,∴5+t>4,∴t>-1,
又∵-5<t<0,
∴t的取值范围为-1<t<0.
第2题解图
3. (1)证明:由OA=OC=2OB=4知,OC=4,OB=2,
又∵四边形ABCD为平行四边形,
∴AD=BC=6,
则点A,B的坐标分别为(0,4),(-2,0),
当y=4时,y=x+t=4,
则x=4-t=4-1=3=AD,
即点P(3,4),
∴AP=DP;
(2)解:PQ=2AP,理由:
由点A,B的坐标,得直线AB的表达式为y=2x+4,
联立上式和y=x+t得2x+4=x+t,
解得x=t-4,
即点Q(t-4,2t-4),
在直线y=x+t中,当y=4时,x=4-t,
∴点P(4-t,4),
则AP=4-t,
由点P,Q的坐标,得PQ=2(4-t)=2AP;
(3)解:存在.如解图①②③,过点P作PH⊥x轴于点H,过点Q作QI⊥x轴于点I,
设点M(m,0),
由(2)知,点P,Q的坐标分别为(4-t,4),(t-4,2t-4),
则HM=|m-4+t|,PH=OA=4,IM=|m-t+4|,QI=|4-2t|,
∵∠PMH+∠QMI=90°,∠QMI+∠IQM=90°,
∴∠IQM=∠PMH,
又∵∠PHM=∠MIQ=90°,
∴△PHM∽△MIQ,
∵以点M,P,Q为顶点的三角形与△AOB相似,
则PM∶QM=2或,
∴Rt△PHM和Rt△MIQ的相似比为2或,
则PH∶MI=HM∶IQ=2或,
当m>0时,如解图①②,
当相似比为2时,如解图①,
==2,
则PH=2MI,MH=2QI,
即4=2(m-t+4)且4-t-m=2(2t-4),
第3题解图①
解得m=,t=,
即点M(,0),t=;
当相似比为时,如解图②,
==,
则PH=MI,MH=QI,
第3题解图②
则2×4=m-(t-4)且2(m-4+t)=4-2t,
解得m=,t=,
则点M(,0),t=;
当m<0时,如解图③,
第3题解图③
当相似比为2时,如解图③,
==2,
则PH=2MI,MH=2QI,
则4=2[(t-4)-m]且4-t-m=2(4-2t),
解得m=-7,t=-1,
即点M(-7,0),t=-1;
当相似比为时,
经验证,该情况不存在,
综上所述,点M(,0),t=或M(,0),t=或M(-7,0),t=-1.
类型三 动面型探究
1. 解:(1)如解图,连接OB',AB',
∵A(4,0),C(0,3),
∴OA=4,OC=3,
由旋转的性质,得C'O=CO=3,OA'=OA=4,
∴∠OCA=∠OC'C,
∵tan∠OCA==,
tan∠B'OC'==,
∴∠OCA=∠B'OC',
∴∠OC'C=∠B'OC',
∴AC∥OB',
∵四边形ABCO为矩形,
∴AC=OB',
∴四边形OCAB'是平行四边形,
∴AB'=OC=3,AB'∥OC,即AB'∥y轴,
∴点B'的坐标为(4,-3);
第1题解图
(2)∵OB平分∠A'OA,
∴∠DOB=∠AOB,
∵BC∥OA,
∴∠DBO=∠AOB,
∴∠DOB=∠DBO,
∴BD=OD,
设CD=x,则BD=BC-CD=4-x,
∴OD=4-x,
在Rt△OCD中,由勾股定理,得OD2=CD2+OC2,
∴(4-x)2=x2+32,解得x=,
∴BD=4-x=.
2. 解:(1)(-4,),(6,2);
【解法提示】∵四边形ODEF为矩形,D(0,),F(-4,0),∴E(-4,),∵四边形OABC为菱形,A(4,0),∴BC=OA=4,∵C(2,2),∴B(6,2).
(2)如解图,过点C作CN⊥OA于点N,
∵C(2,2),
∴ON=2,CN=2,
∴tan∠CON===,
∴∠CON=60°,
过点H作HR⊥x轴于点R,
∵E'F'=,
∴HR=E'F'=,
∵∠COA=60°,
∴OR===1,
∴H(1,),
由平移可知OO'=EE'=t,
∵E(-4,),
∴E'(-4+t,),
∴E'H=1-(-4+t)=5-t,
∵∠E'HO=∠HOF'=60°,
∴E'M=E'H·tan60°=(5-t),
∵在Rt△AGO'中,AO'=OO'-OA=t-4,∠GAO'=∠COA=60°,
∴GO'=AO'·tan 60°=(t-4),
∴S=S矩形O'D'E'F'-S△MHE'-S△AGO'=4-×(5-t)2-×(t-4)2=-t2+9t-,其中t的取值范围是4<t<5.
第2题解图
3. (1)证明:∵DE是△ABC的中位线,
∴DE=BC,AD=AB,
由旋转性质得AD=DE,
∴AB=BC; (3分)
(2)证明:如解图①,连接AA',
∵DE是△ABC的中位线,F为A'B的中点,
∴DA=BD,
∴DF是△ABA'的中位线,
∴2DF=AA',
由旋转性质得△A'DC'≌△ADC,∠A'DA=∠C'DC,A'D=AD,C'D=CD,
∴=,
∴△A'DA∽△C'DC,
∴=,
∴=,
∴2DF·CD=BD·CC'; (7分)
第3题解图①
(3)解:存在点G,使得∠AGD+∠CGE=180°,证明如下:
如解图②,过点D作DF∥BC交AC于点F,过点C作CH⊥AB于点H,DF与CH交于点G,连接EG,AG,
∵DE⊥BC,
∴∠DEB=90°,
在Rt△BDE中,tan B=,BE=3,
∴DE=4,BD=5,cos B=,sin B=, (8分)
在Rt△BCH中,cos B==,BC=BE+CE=3+=,
∴BH=,
∴AH=AD+BD-BH=+5-=,
∴DH=AD-AH=-==AH, (9分)
∵CH⊥AD,
∴△ADG为等腰三角形,
∴∠AGH=∠DGH, (10分)
∵DF∥BC,
∴∠ADG=∠B,∠EDG=90°,
∴tan∠ADG=tan B=,
cos∠ADG=cos B=,
∴=,=,
∵DH=,
∴HG=,DG=, (11分)
∵=,=,
∴=,
∵∠DHG=∠EDG=90°,
∴△DHG∽△EDG,
∴∠DGH=∠EGD, (12分)
∴∠DGE=∠AGH,
∵∠AGC+∠AGH=180°,
∴∠AGC+∠DGE=180°,
∴∠AGD+∠CGE=180°. (13分)
第3题解图②
一题多解法
如解图③,取AD中点M,CE中点N,连接MN,
∵AD是☉M直径,CE是☉N直径,
∴∠AGD=90°,∠CGE=90°,
∴∠AGD+∠CGE=180°,
∵tan B=,BE=3,
∴BD=5,
∵CE=,
∴EN=CE=,
∴BN=BE+EN=,
∵DE⊥CE,
∴DE是☉N的切线,即DE在☉N外,
作NF⊥AB,
∵∠B=∠B,∠BED=∠BFN=90°,
∴△BDE∽△BNF,
∴=,
∴NF=>,即NF>rn,
∴AB在☉N外,
∴G点在四边形ADEC内部.
作MH⊥BC,
∵BM=,tan B=,
∴BH=,MH=,
∴NH=,
∴MN=≈7.4<AM+CN,
∴☉M和☉N有交点.
第3题解图③
同课章节目录
