26.2.1二次函数y=ax2的图象与性质 教案 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 26.2.1二次函数y=ax2的图象与性质 教案 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 433.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 16:57:20 | ||
图片预览


文档简介
第26章 二次函数
26.2 二次函数的图象与性质
1 二次函数y=ax 的图象与性质
一、教学目标
1.正确理解抛物线的有关概念.
2.会用描点法画出二次函数y=ax 的图象,概括出图象的特点.
3.掌握形如y=ax 的二次函数图象的性质,并会应用.
二、教学重难点
重点:理解抛物线的有关概念,掌握二次函数y=ax2的图象与性质.
难点:会用描点法画出二次函数y=ax2的图象以及理解掌握它的性质.
三、教学过程
【新课导入】
[复习引入]教师提问,学生积极做出回答.
我们知道,一次函数的图象是 一条直线 .
反比例函数的图象是 两支曲线 .
那么,二次函数的图象是什么?它有什么特点?反映了二次函数的哪些性质?让我们先来研究最简单的二次函数y=ax2的图象与性质.
你还记得描点法画函数图象的步骤吗?
1.列表 2.描点 3.连线
【新知探究】
(一)二次函数y=ax2的图象与性质
[课件展示]例1:画二次函数y=x2的图象.
(1)列表:在y=x2 中自变量x可以是任意实数,列表表示几组对应值:
x -3 -2 -1 0 1 2 3
y=x2 9 4 1 0 1 4 9
(2)描点:根据表中x,y的数值在坐标平面中描点(x,y).
(3)连线:如图,再用平滑曲线顺次连接各点,就得到y=x2 的图象.
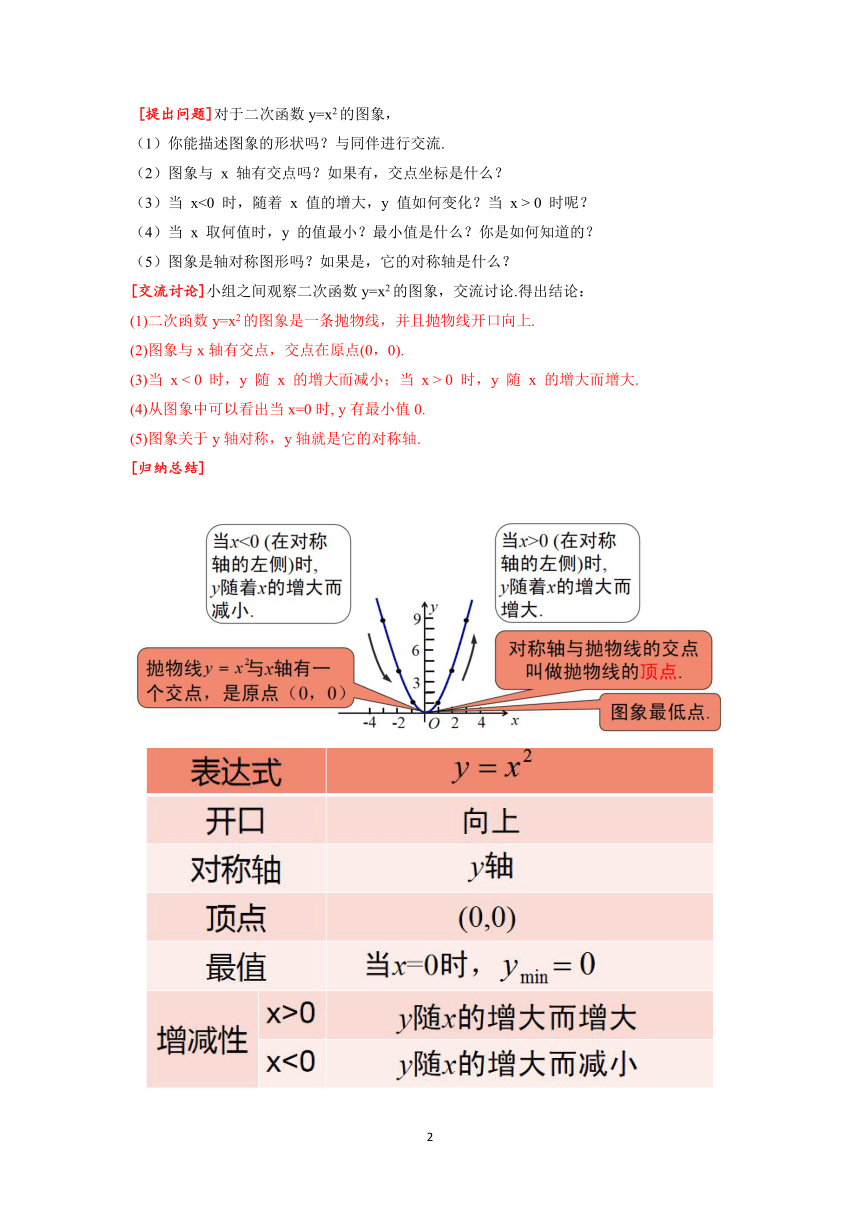
[提出问题]对于二次函数y=x2的图象,
(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象与 x 轴有交点吗?如果有,交点坐标是什么?
(3)当 x<0 时,随着 x 值的增大,y 值如何变化?当 x > 0 时呢?
(4)当 x 取何值时,y 的值最小?最小值是什么?你是如何知道的?
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?
[交流讨论]小组之间观察二次函数y=x2的图象,交流讨论.得出结论:
(1)二次函数y=x2的图象是一条抛物线,并且抛物线开口向上.
(2)图象与x轴有交点,交点在原点(0,0).
(3)当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
(4)从图象中可以看出当x=0时, y有最小值0.
(5)图象关于y轴对称,y轴就是它的对称轴.
[归纳总结]
[课件展示]做一做:二次函数y=-x2的图象是什么形状?先想一想,然后画出它的图象.它与二次函数y=x2的图象有什么关系?与同伴进行交流.
[交流讨论]学生思考问题,动手画出二次函数y=-x2的图象:
(1)列表:
x -3 -2 -1 0 1 2 3
y=-x2 -9 -4 -1 0 -1 -4 -9
(2)描点
(3)连线
小组之间交流讨论,总结:
[课件展示]议一议:观察图象,说说抛物线 y = ax2 与 y = -ax2 (a>0) 有什么关系.
[交流讨论]学生思考问题,小组之间交流讨论,回答问题:
二次项系数互为相反数,开口相反,大小相同,它们关于 x 轴对称.
[提出问题]想一想:在同一直角坐标系中,画出二次函数 ,y =x2,y =2x2的图象.它们的图象有什么相同和不同?
[交流讨论]学生思考问题,动手画出二次函数y=2x2的图象:
(1)列表:
x … -2 -1 0 1 2 …
… 2 0.5 0 0.5 2 …
y=x2 … 4 1 0 1 4 …
y=2x2 … 8 2 0 8 2 …
(2)描点
(3)连线
小组之间交流讨论,总结相同点和不同点:
相同点:1.开口都向上,对称轴都是y轴.
2.当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
3.顶点都是原点(0,0),顶点是抛物线的最低点.
不同点:开口大小不同,抛物线的开口最大,y=2x2抛物线的开口最小.
[课件展示]在同一直角坐标系中,画出二次函数 ,y =-x2,y =-2x2的图象如图,观察其开口大小与a的绝对值有什么关系?
[交流讨论]学生思考问题,小组之间观察函数图象,交流讨论,得出结论:抛物线y=ax2 (a≠0)的形状是由|a|来确定的,|a|越大,开口越小.
【课堂小结】
一、作函数图象的一般步骤:
(1)列表 (2)描点 (3)连线
二、二次函数y=ax2的图象与性质
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
第26章 二次函数
26.2 二次函数的图象与性质
1 二次函数y =ax2 的图象与性质
1.作函数图象的一般步骤:
(1)列表—表中给出一些自变量的值及其对应的函数值;
(2)描点—在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
(3)连线—按照横坐标由小到大顺序,把所描出的各点用平滑的曲线连接起来.
2.二次函数y =ax2 的图象与性质
(1)当a>0时:
开口:向上
对称轴:y轴
顶点:(0,0)
最值:当x=0时,y最小值=0
增减性:当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小
(2)当a<0时:
开口:向下
对称轴:y轴
顶点:(0,0)
最值:当x=0时,y最大值=0
增减性:当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大.
3.二次函数y =ax2 其开口大小与a的绝对值之间的关系
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,|a|越大,开口越小.
【教学反思】
本课时主要探究二次函数y =a x2 的图象与性质 ,在教学中采用了体验探究的教学方式,让学生在教师的配合引导下,自己动手作图,观察、归纳出二次函数的性质,体验知识的形成过程,力求体现“主体参与、自主探索、合作交流、指导引探”的教学理念.
26.2 二次函数的图象与性质
1 二次函数y=ax 的图象与性质
一、教学目标
1.正确理解抛物线的有关概念.
2.会用描点法画出二次函数y=ax 的图象,概括出图象的特点.
3.掌握形如y=ax 的二次函数图象的性质,并会应用.
二、教学重难点
重点:理解抛物线的有关概念,掌握二次函数y=ax2的图象与性质.
难点:会用描点法画出二次函数y=ax2的图象以及理解掌握它的性质.
三、教学过程
【新课导入】
[复习引入]教师提问,学生积极做出回答.
我们知道,一次函数的图象是 一条直线 .
反比例函数的图象是 两支曲线 .
那么,二次函数的图象是什么?它有什么特点?反映了二次函数的哪些性质?让我们先来研究最简单的二次函数y=ax2的图象与性质.
你还记得描点法画函数图象的步骤吗?
1.列表 2.描点 3.连线
【新知探究】
(一)二次函数y=ax2的图象与性质
[课件展示]例1:画二次函数y=x2的图象.
(1)列表:在y=x2 中自变量x可以是任意实数,列表表示几组对应值:
x -3 -2 -1 0 1 2 3
y=x2 9 4 1 0 1 4 9
(2)描点:根据表中x,y的数值在坐标平面中描点(x,y).
(3)连线:如图,再用平滑曲线顺次连接各点,就得到y=x2 的图象.
[提出问题]对于二次函数y=x2的图象,
(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象与 x 轴有交点吗?如果有,交点坐标是什么?
(3)当 x<0 时,随着 x 值的增大,y 值如何变化?当 x > 0 时呢?
(4)当 x 取何值时,y 的值最小?最小值是什么?你是如何知道的?
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?
[交流讨论]小组之间观察二次函数y=x2的图象,交流讨论.得出结论:
(1)二次函数y=x2的图象是一条抛物线,并且抛物线开口向上.
(2)图象与x轴有交点,交点在原点(0,0).
(3)当 x < 0 时,y 随 x 的增大而减小;当 x > 0 时,y 随 x 的增大而增大.
(4)从图象中可以看出当x=0时, y有最小值0.
(5)图象关于y轴对称,y轴就是它的对称轴.
[归纳总结]
[课件展示]做一做:二次函数y=-x2的图象是什么形状?先想一想,然后画出它的图象.它与二次函数y=x2的图象有什么关系?与同伴进行交流.
[交流讨论]学生思考问题,动手画出二次函数y=-x2的图象:
(1)列表:
x -3 -2 -1 0 1 2 3
y=-x2 -9 -4 -1 0 -1 -4 -9
(2)描点
(3)连线
小组之间交流讨论,总结:
[课件展示]议一议:观察图象,说说抛物线 y = ax2 与 y = -ax2 (a>0) 有什么关系.
[交流讨论]学生思考问题,小组之间交流讨论,回答问题:
二次项系数互为相反数,开口相反,大小相同,它们关于 x 轴对称.
[提出问题]想一想:在同一直角坐标系中,画出二次函数 ,y =x2,y =2x2的图象.它们的图象有什么相同和不同?
[交流讨论]学生思考问题,动手画出二次函数y=2x2的图象:
(1)列表:
x … -2 -1 0 1 2 …
… 2 0.5 0 0.5 2 …
y=x2 … 4 1 0 1 4 …
y=2x2 … 8 2 0 8 2 …
(2)描点
(3)连线
小组之间交流讨论,总结相同点和不同点:
相同点:1.开口都向上,对称轴都是y轴.
2.当x<0时,y随x增大而减小;当x>0时,y随x增大而增大.
3.顶点都是原点(0,0),顶点是抛物线的最低点.
不同点:开口大小不同,抛物线的开口最大,y=2x2抛物线的开口最小.
[课件展示]在同一直角坐标系中,画出二次函数 ,y =-x2,y =-2x2的图象如图,观察其开口大小与a的绝对值有什么关系?
[交流讨论]学生思考问题,小组之间观察函数图象,交流讨论,得出结论:抛物线y=ax2 (a≠0)的形状是由|a|来确定的,|a|越大,开口越小.
【课堂小结】
一、作函数图象的一般步骤:
(1)列表 (2)描点 (3)连线
二、二次函数y=ax2的图象与性质
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
第26章 二次函数
26.2 二次函数的图象与性质
1 二次函数y =ax2 的图象与性质
1.作函数图象的一般步骤:
(1)列表—表中给出一些自变量的值及其对应的函数值;
(2)描点—在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
(3)连线—按照横坐标由小到大顺序,把所描出的各点用平滑的曲线连接起来.
2.二次函数y =ax2 的图象与性质
(1)当a>0时:
开口:向上
对称轴:y轴
顶点:(0,0)
最值:当x=0时,y最小值=0
增减性:当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小
(2)当a<0时:
开口:向下
对称轴:y轴
顶点:(0,0)
最值:当x=0时,y最大值=0
增减性:当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大.
3.二次函数y =ax2 其开口大小与a的绝对值之间的关系
抛物线y=ax2 (a≠0)的形状是由|a|来确定的,|a|越大,开口越小.
【教学反思】
本课时主要探究二次函数y =a x2 的图象与性质 ,在教学中采用了体验探究的教学方式,让学生在教师的配合引导下,自己动手作图,观察、归纳出二次函数的性质,体验知识的形成过程,力求体现“主体参与、自主探索、合作交流、指导引探”的教学理念.
