26.3.1 二次函数的实际应用 教案 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 26.3.1 二次函数的实际应用 教案 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 520.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 00:00:00 | ||
图片预览


文档简介
第26章 二次函数
26.3 实践与探索
第1课时 二次函数的实际应用
一、教学目标
1.分析实际问题中变量之间的二次函数关系.
2.能应用二次函数的性质解决图形中最大面积问题.
3.会运用二次函数解决抛物线型问题.
二、教学重难点
重点:能根据实际问题列出函数关系式,并根据问题的实际情况确定自变量取何值时,函数取得最值.
难点:通过建立二次函数的数学模型解决实际问题,在解决问题的过程中体会数形结合思想.
三、教学过程
【新课导入】
[提出问题]生活中有哪些场景可以让你联想到抛物线?(学生回答)
[解答]生活中有很多模型或者场景都能抽象出抛物线的模型,如空中绽放的烟花的瞬间,各种拱桥,彩虹,喷泉,投篮时篮球的运动轨迹等等,那我们在生活中也免不了掌握有关抛物线的实际问题的计算,这节课我们就具体来学习二次函数的实际应用.在开始本节课学习之前,我们先复习下上节课的最值问题,最值问题、顶点问题也是二次函数实际应用中常见的问题类型.
[课件展示]
[提出问题]我们回顾下上节课学过的知识,根据自变量的取值范围求出二次函数 y = ax2 + bx + c 的最小(大)值.当自变量的取值范围是全体实数时,如何确定?(学生回答,教师补充)当自变量的取值范围是x1≤x≤x2时,又如何确定?(学生回答,教师补充)
[过渡]这节课我们就来具体地详细地学习二次函数的实际应用.
【新知探究】
1.用二次函数求几何图形的最大面积
[提出问题]复习完后我们开始今天的学习,首先是常见的面积问题.如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
[课件展示]
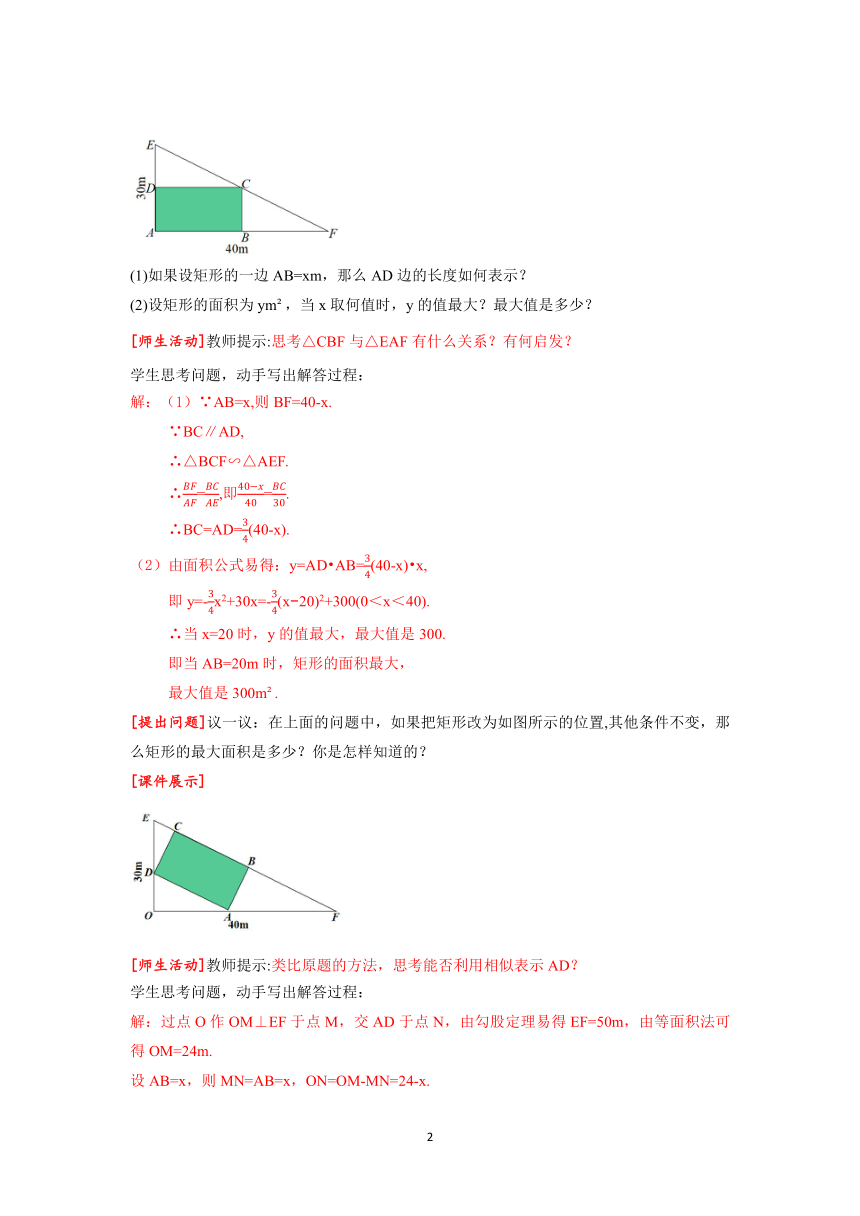
(1)如果设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym ,当x取何值时,y的值最大?最大值是多少?
[师生活动]教师提示:思考△CBF与△EAF有什么关系?有何启发?
学生思考问题,动手写出解答过程:
解:(1)∵AB=x,则BF=40-x.
∵BC∥AD,
∴△BCF∽△AEF.
∴=,即=.
∴BC=AD=(40-x).
(2)由面积公式易得:y=AD AB=(40-x) x,
即y=-x2+30x=-(x 20)2+300(0<x<40).
∴当x=20时,y的值最大,最大值是300.
即当AB=20m时,矩形的面积最大,
最大值是300m .
[提出问题]议一议:在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
[课件展示]
[师生活动]教师提示:类比原题的方法,思考能否利用相似表示AD?
学生思考问题,动手写出解答过程:
解:过点O作OM⊥EF于点M,交AD于点N,由勾股定理易得EF=50m,由等面积法可得OM=24m.
设AB=x,则MN=AB=x,ON=OM-MN=24-x.
由△AOD∽△FOE,得=,
即24 =.∴AD=50-x.
易得y=AD AB=(50-x) x=-(x-12)2+300.
∴当AB=12m时,矩形的面积最大,最大值是300m .
[课件展示]
[提出问题]完成例题的学习接下来请同学们尝试完成如下练习题.某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多?(结果精确到0.01m)此时,窗户的面积是多少?(结果精确到0.01m2)
[课件展示]
[师生活动]教师提示:利用二次函数解决实际问题,必须求出自变量取值范围.
学生思考问题,动手写出解答过程:
解:∵7x+4y+πx=15,∴y=.
∵0<x<15,且0<<15, ∴0<x<1.48.
设窗户的面积是S m2, 则S=+2xy=+2x =-+x=-+.
∴当1.07时,=4.02.
因此,当x约为1.07m时,窗户通过的光线最多.此时,窗户的面积约为4.02 m2.
[归纳总结]二次函数解决几何面积最值问题的方法:
①求出函数表达式和自变量的取值范围;
②配方变形,或利用公式求它的最大值或最小值;
③检查求得的最大值或最小值对应的自变量的值,使之必须在自变量的取值范围内.
[过渡]除了图形面积问题,在几何应用题中,还常见的一种就是含有抛物线型的图形应用题.接下来我们一起继续探究.
利用二次函数解决抛物线型问题
[提出问题]如图,隧道的截面由抛物线和长方形构成.长方形的长是8米,宽是2米,抛物线可以用y=x2+4表示.
[课件展示]
(1)一辆货运卡车高4米,宽2米,它能通过该隧道吗?
(2)如果该隧道内设双向车道,那么这辆货运卡车是否可以通过?
[交流讨论]学生思考问题,小组之间交流讨论,动手写出解答过程:
解 :(1)把y=4-2=2代入y=-x2+4,得2=-x2+4.
解得x=±2√2,则此时可通过货运卡车的宽度为4√2米.
∴高4米,宽2米的卡车能通过该隧道.
(2)由(1),得当y=2时,x=±2√2,
∵2√2>2,∴这两货运卡车能通过.
[提出问题]如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
[课件展示]
[师生活动]教师提示:将实际问题转化为数学问题,先建立适当的坐标系求出这条抛物线表示的二次函数,再根据二次函数的图象进行解题.
学生思考问题,动手写出解答过程:
解: 建立如图所示的平面直角坐标系,设这条抛物线表示的二次函数为y=ax2.
[课件展示]
由抛物线经过点(2,-2),可得-2=a×22.解得a=-.
∴这条抛物线表示的二次函数为y=-x2.
当水面下降1m时,水面的纵坐标为y=-3,
这时有-3=-x2,解得x=±√6 .
∴这时水面宽度为2√6m.
答:当水面下降1m时,水面宽度增加2√6-4m.
[归纳总结]抛物线型问题的一般解题步骤:
①建立适当的平面直角系,并将已知条件转化为点的坐标;
②合理地设出所求的函数的表达式,并代入已知条件或点的坐标,求出关系式;
③利用关系式求解实际问题.
【课堂小结】
实际问题与数学模型之间的相互转化
1.几何面积最值问题
解题关键:依据常见几何图形的面积公式,建立函数关系式;
2.抛物线型问题
转化关键:建立恰当的直角坐标系,能够将实际距离准确的转化为点的坐标;选择运算简便的方法.
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
第26章 二次函数
26.3 实践与探索
第1课时 二次函数的实际应用
1.几何面积最值问题
2.抛物线型问题
【教学反思】
本课时的内容是二次函数的应用问题,开头以生活中常见的事物举例,使抽象出的数学模型更直观,也增加课堂的多样性,增加学生的兴趣.之后又以复习导入,温故知新,有利于学生对知识的融会贯通,灵活运用.通过例题学习总结,练习巩固强化的方法继续探究,故而本节课以启发探究式、讨论式结合的教学方法开展教学活动,以学生探究为主,必要时加以小组合作讨论,充分调动学生学习的积极性和主动性,突出学生的主体地位,达到“不但使学生学会,而且使学生会学”的目的.
26.3 实践与探索
第1课时 二次函数的实际应用
一、教学目标
1.分析实际问题中变量之间的二次函数关系.
2.能应用二次函数的性质解决图形中最大面积问题.
3.会运用二次函数解决抛物线型问题.
二、教学重难点
重点:能根据实际问题列出函数关系式,并根据问题的实际情况确定自变量取何值时,函数取得最值.
难点:通过建立二次函数的数学模型解决实际问题,在解决问题的过程中体会数形结合思想.
三、教学过程
【新课导入】
[提出问题]生活中有哪些场景可以让你联想到抛物线?(学生回答)
[解答]生活中有很多模型或者场景都能抽象出抛物线的模型,如空中绽放的烟花的瞬间,各种拱桥,彩虹,喷泉,投篮时篮球的运动轨迹等等,那我们在生活中也免不了掌握有关抛物线的实际问题的计算,这节课我们就具体来学习二次函数的实际应用.在开始本节课学习之前,我们先复习下上节课的最值问题,最值问题、顶点问题也是二次函数实际应用中常见的问题类型.
[课件展示]
[提出问题]我们回顾下上节课学过的知识,根据自变量的取值范围求出二次函数 y = ax2 + bx + c 的最小(大)值.当自变量的取值范围是全体实数时,如何确定?(学生回答,教师补充)当自变量的取值范围是x1≤x≤x2时,又如何确定?(学生回答,教师补充)
[过渡]这节课我们就来具体地详细地学习二次函数的实际应用.
【新知探究】
1.用二次函数求几何图形的最大面积
[提出问题]复习完后我们开始今天的学习,首先是常见的面积问题.如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和CD分别在两直角边上.
[课件展示]
(1)如果设矩形的一边AB=xm,那么AD边的长度如何表示?
(2)设矩形的面积为ym ,当x取何值时,y的值最大?最大值是多少?
[师生活动]教师提示:思考△CBF与△EAF有什么关系?有何启发?
学生思考问题,动手写出解答过程:
解:(1)∵AB=x,则BF=40-x.
∵BC∥AD,
∴△BCF∽△AEF.
∴=,即=.
∴BC=AD=(40-x).
(2)由面积公式易得:y=AD AB=(40-x) x,
即y=-x2+30x=-(x 20)2+300(0<x<40).
∴当x=20时,y的值最大,最大值是300.
即当AB=20m时,矩形的面积最大,
最大值是300m .
[提出问题]议一议:在上面的问题中,如果把矩形改为如图所示的位置,其他条件不变,那么矩形的最大面积是多少?你是怎样知道的?
[课件展示]
[师生活动]教师提示:类比原题的方法,思考能否利用相似表示AD?
学生思考问题,动手写出解答过程:
解:过点O作OM⊥EF于点M,交AD于点N,由勾股定理易得EF=50m,由等面积法可得OM=24m.
设AB=x,则MN=AB=x,ON=OM-MN=24-x.
由△AOD∽△FOE,得=,
即24 =.∴AD=50-x.
易得y=AD AB=(50-x) x=-(x-12)2+300.
∴当AB=12m时,矩形的面积最大,最大值是300m .
[课件展示]
[提出问题]完成例题的学习接下来请同学们尝试完成如下练习题.某建筑物的窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗框的材料总长(图中所有黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多?(结果精确到0.01m)此时,窗户的面积是多少?(结果精确到0.01m2)
[课件展示]
[师生活动]教师提示:利用二次函数解决实际问题,必须求出自变量取值范围.
学生思考问题,动手写出解答过程:
解:∵7x+4y+πx=15,∴y=.
∵0<x<15,且0<<15, ∴0<x<1.48.
设窗户的面积是S m2, 则S=+2xy=+2x =-+x=-+.
∴当1.07时,=4.02.
因此,当x约为1.07m时,窗户通过的光线最多.此时,窗户的面积约为4.02 m2.
[归纳总结]二次函数解决几何面积最值问题的方法:
①求出函数表达式和自变量的取值范围;
②配方变形,或利用公式求它的最大值或最小值;
③检查求得的最大值或最小值对应的自变量的值,使之必须在自变量的取值范围内.
[过渡]除了图形面积问题,在几何应用题中,还常见的一种就是含有抛物线型的图形应用题.接下来我们一起继续探究.
利用二次函数解决抛物线型问题
[提出问题]如图,隧道的截面由抛物线和长方形构成.长方形的长是8米,宽是2米,抛物线可以用y=x2+4表示.
[课件展示]
(1)一辆货运卡车高4米,宽2米,它能通过该隧道吗?
(2)如果该隧道内设双向车道,那么这辆货运卡车是否可以通过?
[交流讨论]学生思考问题,小组之间交流讨论,动手写出解答过程:
解 :(1)把y=4-2=2代入y=-x2+4,得2=-x2+4.
解得x=±2√2,则此时可通过货运卡车的宽度为4√2米.
∴高4米,宽2米的卡车能通过该隧道.
(2)由(1),得当y=2时,x=±2√2,
∵2√2>2,∴这两货运卡车能通过.
[提出问题]如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
[课件展示]
[师生活动]教师提示:将实际问题转化为数学问题,先建立适当的坐标系求出这条抛物线表示的二次函数,再根据二次函数的图象进行解题.
学生思考问题,动手写出解答过程:
解: 建立如图所示的平面直角坐标系,设这条抛物线表示的二次函数为y=ax2.
[课件展示]
由抛物线经过点(2,-2),可得-2=a×22.解得a=-.
∴这条抛物线表示的二次函数为y=-x2.
当水面下降1m时,水面的纵坐标为y=-3,
这时有-3=-x2,解得x=±√6 .
∴这时水面宽度为2√6m.
答:当水面下降1m时,水面宽度增加2√6-4m.
[归纳总结]抛物线型问题的一般解题步骤:
①建立适当的平面直角系,并将已知条件转化为点的坐标;
②合理地设出所求的函数的表达式,并代入已知条件或点的坐标,求出关系式;
③利用关系式求解实际问题.
【课堂小结】
实际问题与数学模型之间的相互转化
1.几何面积最值问题
解题关键:依据常见几何图形的面积公式,建立函数关系式;
2.抛物线型问题
转化关键:建立恰当的直角坐标系,能够将实际距离准确的转化为点的坐标;选择运算简便的方法.
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
第26章 二次函数
26.3 实践与探索
第1课时 二次函数的实际应用
1.几何面积最值问题
2.抛物线型问题
【教学反思】
本课时的内容是二次函数的应用问题,开头以生活中常见的事物举例,使抽象出的数学模型更直观,也增加课堂的多样性,增加学生的兴趣.之后又以复习导入,温故知新,有利于学生对知识的融会贯通,灵活运用.通过例题学习总结,练习巩固强化的方法继续探究,故而本节课以启发探究式、讨论式结合的教学方法开展教学活动,以学生探究为主,必要时加以小组合作讨论,充分调动学生学习的积极性和主动性,突出学生的主体地位,达到“不但使学生学会,而且使学生会学”的目的.
