27.1.2 第2课时 垂径定理 教案 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.1.2 第2课时 垂径定理 教案 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | doc | ||
| 文件大小 | 516.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 17:20:24 | ||
图片预览



文档简介
第27章 圆
27.1 圆的认识
2.圆的对称性
第2课时 垂径定理
一、教学目标
掌握垂径定理及其推论,理解垂径定理的推导过程,并能运用垂径定理解决相关问题.
二、教学重难点
重点:理解垂径定理和推论的内容,并会证明,利用垂径定理解决与圆有关的问题.
难点:利用垂径定理及其推论解决实际问题.
三、教学过程
【新课导入】
[情境导入]
你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
【新知探究】
(一)垂径定理及其推论
[提出问题]
做一做:剪一个圆形纸片,在圆形纸片上任意画一条垂直于直径CD的弦,垂足为点P,再将纸片沿着直径CD对折,分别比较AP与BP、弧AC与弧BC,你能发现什么结论?
[交流讨论]
小组之间交流讨论.得出结论:对折后,CD两侧的两个半圆重合,点A与点B重合,AP与BP重合,弧AC和弧BC,弧AD与弧BD重合,即它们都是相等的.
试一试:能不能用所学过的知识证明你的结论?
已知:在在☉O中,CD是直径,AB是弦,AB⊥CD,垂足为P.
求证:AP=BP,.
证明:连结CA、CB、OA、OB,则OA=OB,即△AOB是等腰三角形.
∵CD⊥AB,∴AP=BP.
又∵CP=CP,∴Rt△APC≌Rt△BPC.
∴AC=BC,
∴(在同一个圆中,如果弦相等,那么它们所对的弧相等).
由此易得.
[归纳总结]
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
几何语言描述:
∵CD是直径,CD⊥AB,(条件)
∴AP=BP,.(结论)
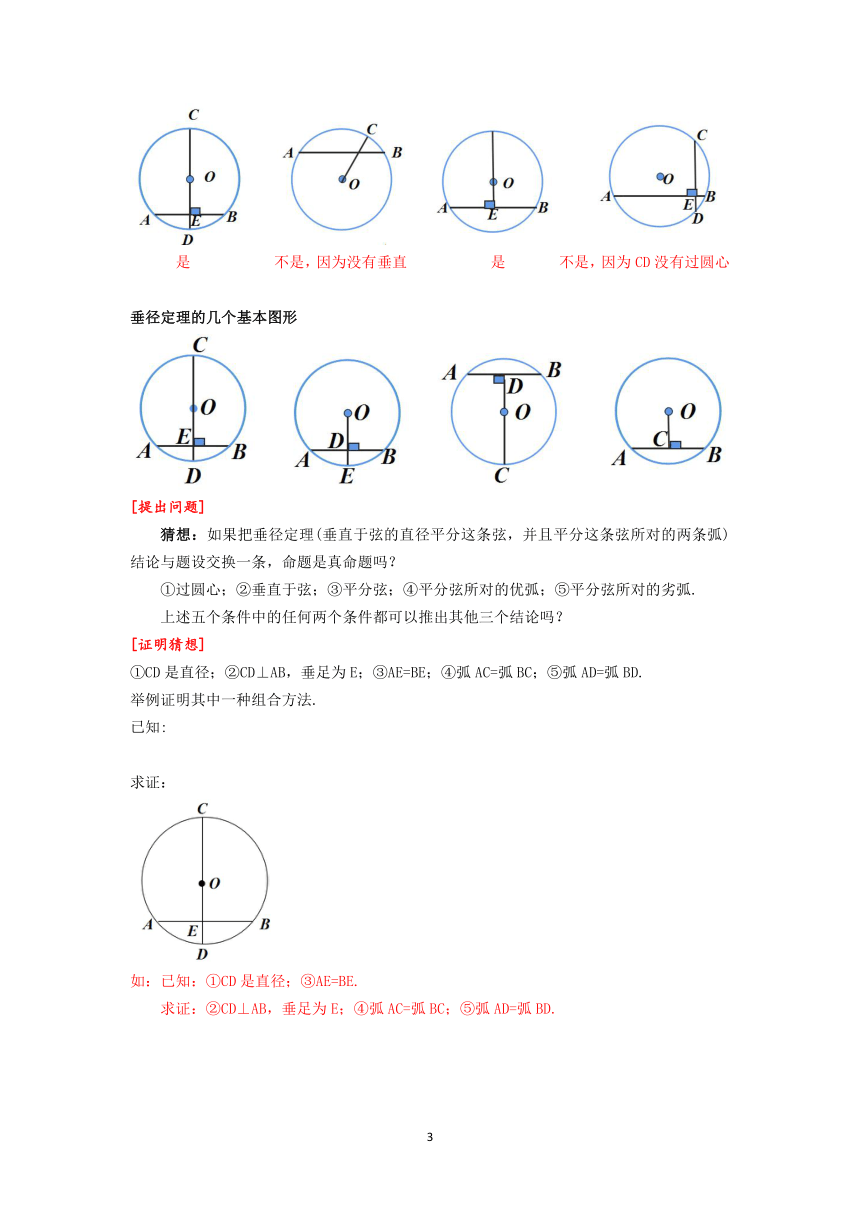
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是 不是,因为没有垂直 是 不是,因为CD没有过圆心
垂径定理的几个基本图形
[提出问题]
猜想:如果把垂径定理(垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
[证明猜想]
①CD是直径;②CD⊥AB,垂足为E;③AE=BE;④弧AC=弧BC;⑤弧AD=弧BD.
举例证明其中一种组合方法.
已知:
求证:
如:已知:①CD是直径;③AE=BE.
求证:②CD⊥AB,垂足为E;④弧AC=弧BC;⑤弧AD=弧BD.
[证明举例]
如图,AB是⊙O的一条弦,作直径CD,使AM=BM.
(1)CD⊥AB吗?为什么?
(2)弧AC与弧BC相等吗?弧AD与弧BD相等吗?为什么?
解:(1)连结AO,BO,则AO=BO,
又AM=BM,∴△AOM≌△BOM(SSS),
∴∠AMO=∠BMO=90°,
∴CD⊥AB.
(2)由垂径定理可得弧AC弧=BC,弧AD=弧BD.
[归纳总结]
垂径定理的推论:
平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
几何语言描述:
∵CD是直径,AE=BE,(条件)
∴AB⊥CD,.(结论)
平分弧的直径垂直平分这条弧所对的弦.
几何语言描述:
∵CD是直径,(或),(条件)
∴AB⊥CD,AE=BE.(结论)
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
特别说明:圆的两条直径是互相平分的.
垂径定理的本质:
(二)垂径定理及其推论的计算
【例1】如图,⊙O的半径长为10,OC⊥AB,垂足为E.若OE=6,则弦AB的长为 16 .
【解析】连结OA,在Rt△AOE中,由勾股定理,得AE==8.由垂径定理,得AB=2AE=16.
【例2】如图,⊙O的弦AB=8cm,直径CE⊥AB于D,DC=2cm,求半径OC的长.
解:连接OA.∵CE⊥AB于点D,
∴AD=AB=4cm.
设OC=xcm,则OD=(x-2)cm,根据勾股定理,得x2=42+(x-2)2,
解得x=5,即半径OC的长为5cm.
[实际应用]
【例3】你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴AB=37m,CD=7.23m.
∴AD=AB=18.5m,OD=OC-CD=(R-7.23)m.
在Rt△AOD中,由勾股定理,得R2=18.52+(R-7.23)2.
解得R≈27.3.即主桥拱半径约为27.3m.
【例4】如图1、2,一弓形弦长为cm,弓形所在的圆的半径为7cm,则弓形的高为 2cm或12cm .
[方法归纳]
涉及垂径定理时辅助线的添加方法:
在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
弓形中重要数量关系:
弦a,弦心距d,弓形高h,半径r之间有以下关系:d+h=r,r =d +() .
【课堂小结】
一、垂径定理及其推论
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.
二、垂径定理及其推论的计算
【课堂训练】
1.下列说法正确的是( D )
A.垂直于弦的直线平分弦所对的两条弧 B.平分弦的直径垂直于弦
C.垂直于直径的直线平分这条直径 D.弦的垂直平分线经过圆心
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( D )
A.CM=DM B.弧CB=弧DB
C.∠ACD=∠ADC D.OM=MB
3.(2022泸州)如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4,DE=4,则BC的长是( C )
A.1 B. C.2 D.4
4.(2023永州)如图,⊙O是一个盛有水的容器的横截面,⊙O的半径为10cm,水的最深处到水面AB的距离为4cm,则水面AB的宽度为 16 cm.
5.如图所示,在⊙O中,AB为⊙O的弦,C,D是直线AB上两点,且AC=BD.
求证:△OCD为等腰三角形.
证明:过点O作OM⊥AB,垂足为M,
∵OM⊥AB,∴AM=BM.
∵AC=BD,∴CM=DM.
又∵OM⊥CD,∴OC=OD.
∴△OCD为等腰三角形.
6.⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB与CD的距离为 14cm或2cm .
【提示】由于两弦的位置不确定,因此需要分类讨论.
【布置作业】
【板书设计】
第2课时 垂径定理
1.垂径定理
2.垂径定理的推论
【教学反思】
垂径定理是圆中一个重要的定理,由于它涉及的条件结论比较多,学生容易搞混淆,本节课通过对剪圆和折叠圆的操作,调动学生的积极性,活跃课堂气氛.让学生在操作、分析、归纳的基础上,掌握垂径定理及其推论,同时引导学生归纳垂径定理时加深对全等三角形或等腰三角形知识的复习和应用.
27.1 圆的认识
2.圆的对称性
第2课时 垂径定理
一、教学目标
掌握垂径定理及其推论,理解垂径定理的推导过程,并能运用垂径定理解决相关问题.
二、教学重难点
重点:理解垂径定理和推论的内容,并会证明,利用垂径定理解决与圆有关的问题.
难点:利用垂径定理及其推论解决实际问题.
三、教学过程
【新课导入】
[情境导入]
你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
【新知探究】
(一)垂径定理及其推论
[提出问题]
做一做:剪一个圆形纸片,在圆形纸片上任意画一条垂直于直径CD的弦,垂足为点P,再将纸片沿着直径CD对折,分别比较AP与BP、弧AC与弧BC,你能发现什么结论?
[交流讨论]
小组之间交流讨论.得出结论:对折后,CD两侧的两个半圆重合,点A与点B重合,AP与BP重合,弧AC和弧BC,弧AD与弧BD重合,即它们都是相等的.
试一试:能不能用所学过的知识证明你的结论?
已知:在在☉O中,CD是直径,AB是弦,AB⊥CD,垂足为P.
求证:AP=BP,.
证明:连结CA、CB、OA、OB,则OA=OB,即△AOB是等腰三角形.
∵CD⊥AB,∴AP=BP.
又∵CP=CP,∴Rt△APC≌Rt△BPC.
∴AC=BC,
∴(在同一个圆中,如果弦相等,那么它们所对的弧相等).
由此易得.
[归纳总结]
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
几何语言描述:
∵CD是直径,CD⊥AB,(条件)
∴AP=BP,.(结论)
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是 不是,因为没有垂直 是 不是,因为CD没有过圆心
垂径定理的几个基本图形
[提出问题]
猜想:如果把垂径定理(垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
[证明猜想]
①CD是直径;②CD⊥AB,垂足为E;③AE=BE;④弧AC=弧BC;⑤弧AD=弧BD.
举例证明其中一种组合方法.
已知:
求证:
如:已知:①CD是直径;③AE=BE.
求证:②CD⊥AB,垂足为E;④弧AC=弧BC;⑤弧AD=弧BD.
[证明举例]
如图,AB是⊙O的一条弦,作直径CD,使AM=BM.
(1)CD⊥AB吗?为什么?
(2)弧AC与弧BC相等吗?弧AD与弧BD相等吗?为什么?
解:(1)连结AO,BO,则AO=BO,
又AM=BM,∴△AOM≌△BOM(SSS),
∴∠AMO=∠BMO=90°,
∴CD⊥AB.
(2)由垂径定理可得弧AC弧=BC,弧AD=弧BD.
[归纳总结]
垂径定理的推论:
平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
几何语言描述:
∵CD是直径,AE=BE,(条件)
∴AB⊥CD,.(结论)
平分弧的直径垂直平分这条弧所对的弦.
几何语言描述:
∵CD是直径,(或),(条件)
∴AB⊥CD,AE=BE.(结论)
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
特别说明:圆的两条直径是互相平分的.
垂径定理的本质:
(二)垂径定理及其推论的计算
【例1】如图,⊙O的半径长为10,OC⊥AB,垂足为E.若OE=6,则弦AB的长为 16 .
【解析】连结OA,在Rt△AOE中,由勾股定理,得AE==8.由垂径定理,得AB=2AE=16.
【例2】如图,⊙O的弦AB=8cm,直径CE⊥AB于D,DC=2cm,求半径OC的长.
解:连接OA.∵CE⊥AB于点D,
∴AD=AB=4cm.
设OC=xcm,则OD=(x-2)cm,根据勾股定理,得x2=42+(x-2)2,
解得x=5,即半径OC的长为5cm.
[实际应用]
【例3】你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
∴AB=37m,CD=7.23m.
∴AD=AB=18.5m,OD=OC-CD=(R-7.23)m.
在Rt△AOD中,由勾股定理,得R2=18.52+(R-7.23)2.
解得R≈27.3.即主桥拱半径约为27.3m.
【例4】如图1、2,一弓形弦长为cm,弓形所在的圆的半径为7cm,则弓形的高为 2cm或12cm .
[方法归纳]
涉及垂径定理时辅助线的添加方法:
在圆中有关弦长a,半径r,弦心距d(圆心到弦的距离),弓形高h的计算题时,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
弓形中重要数量关系:
弦a,弦心距d,弓形高h,半径r之间有以下关系:d+h=r,r =d +() .
【课堂小结】
一、垂径定理及其推论
垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.
二、垂径定理及其推论的计算
【课堂训练】
1.下列说法正确的是( D )
A.垂直于弦的直线平分弦所对的两条弧 B.平分弦的直径垂直于弦
C.垂直于直径的直线平分这条直径 D.弦的垂直平分线经过圆心
2.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( D )
A.CM=DM B.弧CB=弧DB
C.∠ACD=∠ADC D.OM=MB
3.(2022泸州)如图,AB是⊙O的直径,OD垂直于弦AC于点D,DO的延长线交⊙O于点E.若AC=4,DE=4,则BC的长是( C )
A.1 B. C.2 D.4
4.(2023永州)如图,⊙O是一个盛有水的容器的横截面,⊙O的半径为10cm,水的最深处到水面AB的距离为4cm,则水面AB的宽度为 16 cm.
5.如图所示,在⊙O中,AB为⊙O的弦,C,D是直线AB上两点,且AC=BD.
求证:△OCD为等腰三角形.
证明:过点O作OM⊥AB,垂足为M,
∵OM⊥AB,∴AM=BM.
∵AC=BD,∴CM=DM.
又∵OM⊥CD,∴OC=OD.
∴△OCD为等腰三角形.
6.⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB与CD的距离为 14cm或2cm .
【提示】由于两弦的位置不确定,因此需要分类讨论.
【布置作业】
【板书设计】
第2课时 垂径定理
1.垂径定理
2.垂径定理的推论
【教学反思】
垂径定理是圆中一个重要的定理,由于它涉及的条件结论比较多,学生容易搞混淆,本节课通过对剪圆和折叠圆的操作,调动学生的积极性,活跃课堂气氛.让学生在操作、分析、归纳的基础上,掌握垂径定理及其推论,同时引导学生归纳垂径定理时加深对全等三角形或等腰三角形知识的复习和应用.
