27.2.2 直线与圆的位置关系 教案 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.2.2 直线与圆的位置关系 教案 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 457.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 17:21:23 | ||
图片预览

文档简介
第27章 圆
27.2 与圆有关的位置关系
2.直线与圆的位置关系
一、教学目标
1.了解直线和圆的位置关系;
2.理解直线和圆的三种位置关系圆心到直线的距离d和圆的半径r之间的数量关系.
二、教学重难点
重点:了解直线与圆的不同位置关系时的有关概念
难点:能运用直线与圆的位置关系解决实际问题
三、教学过程
【新课导入】
[提出问题]上节课我们学习了点和圆的位置关系,我们先来复习下,点和圆的位置关系有几种?用数量关系如何来判断呢?(提问学生回答)
[解答]学生回答后,教师明确:点在圆内,d<r;点在圆上,d=r;点在圆外,d>r.
[提出问题]那这节课我们继续学习与圆有关的位置关系中,直线与圆的位置关系.看课件上的图片,想一想如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
[课件展示]
[解答]学生回答后,教师明确:如图1所示,直线和圆的公共点个数有2个;如图2所示,直线和圆的公共点个数有1个;如图3所示,直线和圆没有公共点.因此可以猜测直线和圆有3种位置关系.
[提出问题]接下来请同学在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
[解答]学生回答后,教师明确:公共点个数最少时没有公共点,可能有一个公共点,最多有两个公共点.通过生活中的例子和自己的动手操作我们能确定直线和圆的3种关系,本节课我们就具体来学习直线和圆的位置关系.
【新知探究】
直线与圆的位置关系
[解答]如图所示,第一种情况,就类似太阳完全升起时的情况.如果一条直线与一个圆没有公共点,那么我们就说这条直线与这个圆相离.同样我们可以反过来说,如果直线和圆相离,那么此时圆和直线是否有公共点?(学生齐答:没有)公共点个数是多少?(学生齐答:0)
[课件展示]
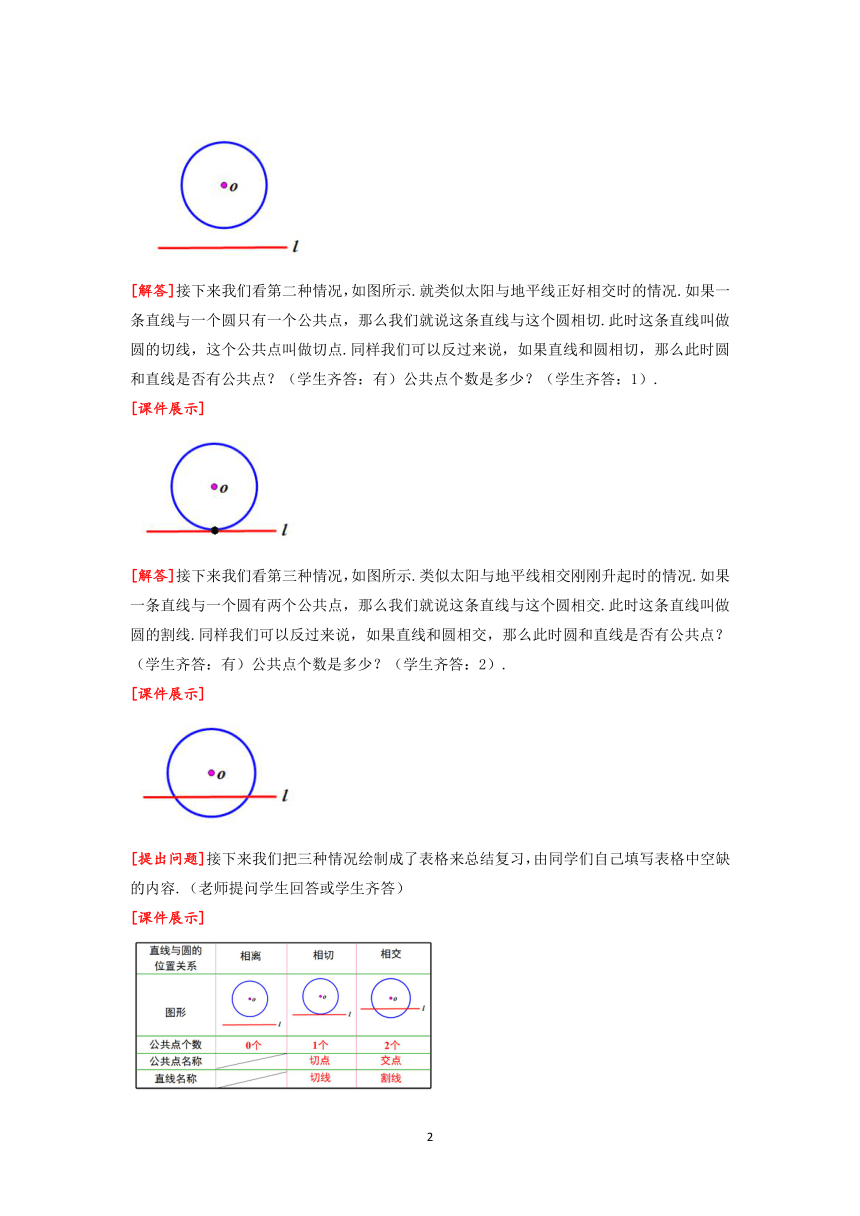
[解答]接下来我们看第二种情况,如图所示.就类似太阳与地平线正好相交时的情况.如果一条直线与一个圆只有一个公共点,那么我们就说这条直线与这个圆相切.此时这条直线叫做圆的切线,这个公共点叫做切点.同样我们可以反过来说,如果直线和圆相切,那么此时圆和直线是否有公共点?(学生齐答:有)公共点个数是多少?(学生齐答:1).
[课件展示]
[解答]接下来我们看第三种情况,如图所示.类似太阳与地平线相交刚刚升起时的情况.如果一条直线与一个圆有两个公共点,那么我们就说这条直线与这个圆相交.此时这条直线叫做圆的割线.同样我们可以反过来说,如果直线和圆相交,那么此时圆和直线是否有公共点?(学生齐答:有)公共点个数是多少?(学生齐答:2).
[课件展示]
[提出问题]接下来我们把三种情况绘制成了表格来总结复习,由同学们自己填写表格中空缺的内容.(老师提问学生回答或学生齐答)
[课件展示]
[提出问题]接下来我们看几道判断题,我们分成几个小组,分别作答,并且由同学们解释原因.教师明确补充.
[课件展示]
用数量关系判断直线与圆的位置关系
[提出问题]同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
[解答]教师明确:圆心到直线的距离也在改变:首先距离大于半径,然后距离等于半径,最后距离小于半径.我们说点到直线的距离是指从直线外一点 (A) 到直线 (l) 的垂线段 (OA) 的长度.
[提出问题]那我们思考下怎样用圆心到直线的距离 d 来判定直线 l 与 ⊙O 的位置关系呢?
[解答]教师明确:可以通过圆心O到直线的距离d与圆的半径r的关系来区分.当直线和圆相交时,d< r;当直线和圆相切时,d= r;当直线和圆相离时,d> r.那反过来我们也可以总结,当d< r时,直线和圆相交;当d= r时,直线和圆相切;当d> r时,直线和圆相离.这也是我们数学学习中重要的数形结合,通过位置关系可以推出数量关系,推出公共点个数;反过来,通过公共点个数,我们可以推出数量关系,推出位置关系.
[提出问题]结合我们今天学习的知识,我们来看一道例题,学生自己尝试解答.(提示:分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出点C到AB的距离d.)(学生解答后教师明确答案)
[课件展示]
[归纳总结]今天我们学习了直线与圆的三种位置关系,分别是相切、相交和相离,并了解了交点的个数,之后我们又学了用数量关系判断直线与圆的位置关系,即通过半径和圆心和直线的距离关系判断直线与圆的位置关系,并判断交点个数,反过来也能推出.
【课堂小结】
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
圆
27.2 与圆有关的位置关系
2. 直线与圆的位置关系
1.直线与圆的位置关系
相离、相切、相交
交点个数:0/1/2
2.用数量关系判断直线与圆的位置关系
d>r,d=r,d<r
【教学反思】
一、案例的“亮点”
1.通过复习已经学过的知识,让学生既能温习学过的知识,又能和即将学习的新的知识产生联系,让知识之间互相关联;通过生活中太阳与海平面的关系,抽象出直线和圆的位置关系,并通过学生自己动手操作,进一步了解到直线和圆的位置关系,增加学习的兴趣.
2.数形结合思想,充分学习直线和圆的位置关系,学习三种情况下交点的情况,进一步学习用数量关系判断直线与圆的位置关系,即通过半径和圆心和直线的距离关系判断直线与圆的位置关系,并判断交点个数,反过来也能推出.
二、教学中易出现的问题
学生小组讨论的过程中,注意学生是否参与到问题的探究中,总结知识点的过程中注意对学生的引导,让学生自己能够总结出相应的答案、结论与定义.教学过程中,强调学生从实际生活中感受,体会直线与圆的几种位置关系,并会用数学语言来描述归纳,经历将实际问题转化为数学问题的过程,即数形结合思想的感受与理解.
27.2 与圆有关的位置关系
2.直线与圆的位置关系
一、教学目标
1.了解直线和圆的位置关系;
2.理解直线和圆的三种位置关系圆心到直线的距离d和圆的半径r之间的数量关系.
二、教学重难点
重点:了解直线与圆的不同位置关系时的有关概念
难点:能运用直线与圆的位置关系解决实际问题
三、教学过程
【新课导入】
[提出问题]上节课我们学习了点和圆的位置关系,我们先来复习下,点和圆的位置关系有几种?用数量关系如何来判断呢?(提问学生回答)
[解答]学生回答后,教师明确:点在圆内,d<r;点在圆上,d=r;点在圆外,d>r.
[提出问题]那这节课我们继续学习与圆有关的位置关系中,直线与圆的位置关系.看课件上的图片,想一想如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
[课件展示]
[解答]学生回答后,教师明确:如图1所示,直线和圆的公共点个数有2个;如图2所示,直线和圆的公共点个数有1个;如图3所示,直线和圆没有公共点.因此可以猜测直线和圆有3种位置关系.
[提出问题]接下来请同学在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
[解答]学生回答后,教师明确:公共点个数最少时没有公共点,可能有一个公共点,最多有两个公共点.通过生活中的例子和自己的动手操作我们能确定直线和圆的3种关系,本节课我们就具体来学习直线和圆的位置关系.
【新知探究】
直线与圆的位置关系
[解答]如图所示,第一种情况,就类似太阳完全升起时的情况.如果一条直线与一个圆没有公共点,那么我们就说这条直线与这个圆相离.同样我们可以反过来说,如果直线和圆相离,那么此时圆和直线是否有公共点?(学生齐答:没有)公共点个数是多少?(学生齐答:0)
[课件展示]
[解答]接下来我们看第二种情况,如图所示.就类似太阳与地平线正好相交时的情况.如果一条直线与一个圆只有一个公共点,那么我们就说这条直线与这个圆相切.此时这条直线叫做圆的切线,这个公共点叫做切点.同样我们可以反过来说,如果直线和圆相切,那么此时圆和直线是否有公共点?(学生齐答:有)公共点个数是多少?(学生齐答:1).
[课件展示]
[解答]接下来我们看第三种情况,如图所示.类似太阳与地平线相交刚刚升起时的情况.如果一条直线与一个圆有两个公共点,那么我们就说这条直线与这个圆相交.此时这条直线叫做圆的割线.同样我们可以反过来说,如果直线和圆相交,那么此时圆和直线是否有公共点?(学生齐答:有)公共点个数是多少?(学生齐答:2).
[课件展示]
[提出问题]接下来我们把三种情况绘制成了表格来总结复习,由同学们自己填写表格中空缺的内容.(老师提问学生回答或学生齐答)
[课件展示]
[提出问题]接下来我们看几道判断题,我们分成几个小组,分别作答,并且由同学们解释原因.教师明确补充.
[课件展示]
用数量关系判断直线与圆的位置关系
[提出问题]同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
[解答]教师明确:圆心到直线的距离也在改变:首先距离大于半径,然后距离等于半径,最后距离小于半径.我们说点到直线的距离是指从直线外一点 (A) 到直线 (l) 的垂线段 (OA) 的长度.
[提出问题]那我们思考下怎样用圆心到直线的距离 d 来判定直线 l 与 ⊙O 的位置关系呢?
[解答]教师明确:可以通过圆心O到直线的距离d与圆的半径r的关系来区分.当直线和圆相交时,d< r;当直线和圆相切时,d= r;当直线和圆相离时,d> r.那反过来我们也可以总结,当d< r时,直线和圆相交;当d= r时,直线和圆相切;当d> r时,直线和圆相离.这也是我们数学学习中重要的数形结合,通过位置关系可以推出数量关系,推出公共点个数;反过来,通过公共点个数,我们可以推出数量关系,推出位置关系.
[提出问题]结合我们今天学习的知识,我们来看一道例题,学生自己尝试解答.(提示:分析:要了解AB与⊙C的位置关系,只要知道圆心C到AB的距离d与r的关系.已知r,只需求出点C到AB的距离d.)(学生解答后教师明确答案)
[课件展示]
[归纳总结]今天我们学习了直线与圆的三种位置关系,分别是相切、相交和相离,并了解了交点的个数,之后我们又学了用数量关系判断直线与圆的位置关系,即通过半径和圆心和直线的距离关系判断直线与圆的位置关系,并判断交点个数,反过来也能推出.
【课堂小结】
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
圆
27.2 与圆有关的位置关系
2. 直线与圆的位置关系
1.直线与圆的位置关系
相离、相切、相交
交点个数:0/1/2
2.用数量关系判断直线与圆的位置关系
d>r,d=r,d<r
【教学反思】
一、案例的“亮点”
1.通过复习已经学过的知识,让学生既能温习学过的知识,又能和即将学习的新的知识产生联系,让知识之间互相关联;通过生活中太阳与海平面的关系,抽象出直线和圆的位置关系,并通过学生自己动手操作,进一步了解到直线和圆的位置关系,增加学习的兴趣.
2.数形结合思想,充分学习直线和圆的位置关系,学习三种情况下交点的情况,进一步学习用数量关系判断直线与圆的位置关系,即通过半径和圆心和直线的距离关系判断直线与圆的位置关系,并判断交点个数,反过来也能推出.
二、教学中易出现的问题
学生小组讨论的过程中,注意学生是否参与到问题的探究中,总结知识点的过程中注意对学生的引导,让学生自己能够总结出相应的答案、结论与定义.教学过程中,强调学生从实际生活中感受,体会直线与圆的几种位置关系,并会用数学语言来描述归纳,经历将实际问题转化为数学问题的过程,即数形结合思想的感受与理解.
