27.2.3 第2课时 切线长定理和三角形的内切圆 教案 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.2.3 第2课时 切线长定理和三角形的内切圆 教案 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 534.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 17:21:44 | ||
图片预览

文档简介
第27章 圆
27.2 与圆有关的位置关系
3.切线
第2课时 切线长定理及三角形的内切圆
一、教学目标
1.理解并掌握切线长定理;
2.了解三角形的内心、内切圆及外切三角形的概念.
二、教学重难点
重点:掌握切线长定理,初步学会运用切线长定理进行计算与证明
难点:了解有关三角形的内切圆和三角形的内心的概念
【新课导入】
[提出问题]看课件上的图片,当同学们在抖空竹时,当同学们把篮球夹在胳膊中,当同学们在玩悠悠球时,如图所示的时刻的情景,你能从中抽象出什么样的数学图形?(教师展示图片,学生描述后展示图片中的数学图形)
[课件展示]
[过渡]从图中的模型可以看出为一个圆和两条切线,本节课我们就来学习这个模型及和圆的切线有关的知识.
【新知探究】
切线长定理
[提出问题]从圆外一点引圆的切线,最多能作出几条切线?(展示图片,教师明确2条)
这一点和切点之间的线段的长叫做切线长.
[课件展示]
[解答]这一点和切点之间的线段的长叫做切线长.
[提出问题]切线和切线长是一个意思吗?
[解答]切线和切线长是两个不同的概念:切线是一条与圆相切的直线,不能度量,而切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.二者的联系是都垂直于过切点的半径.
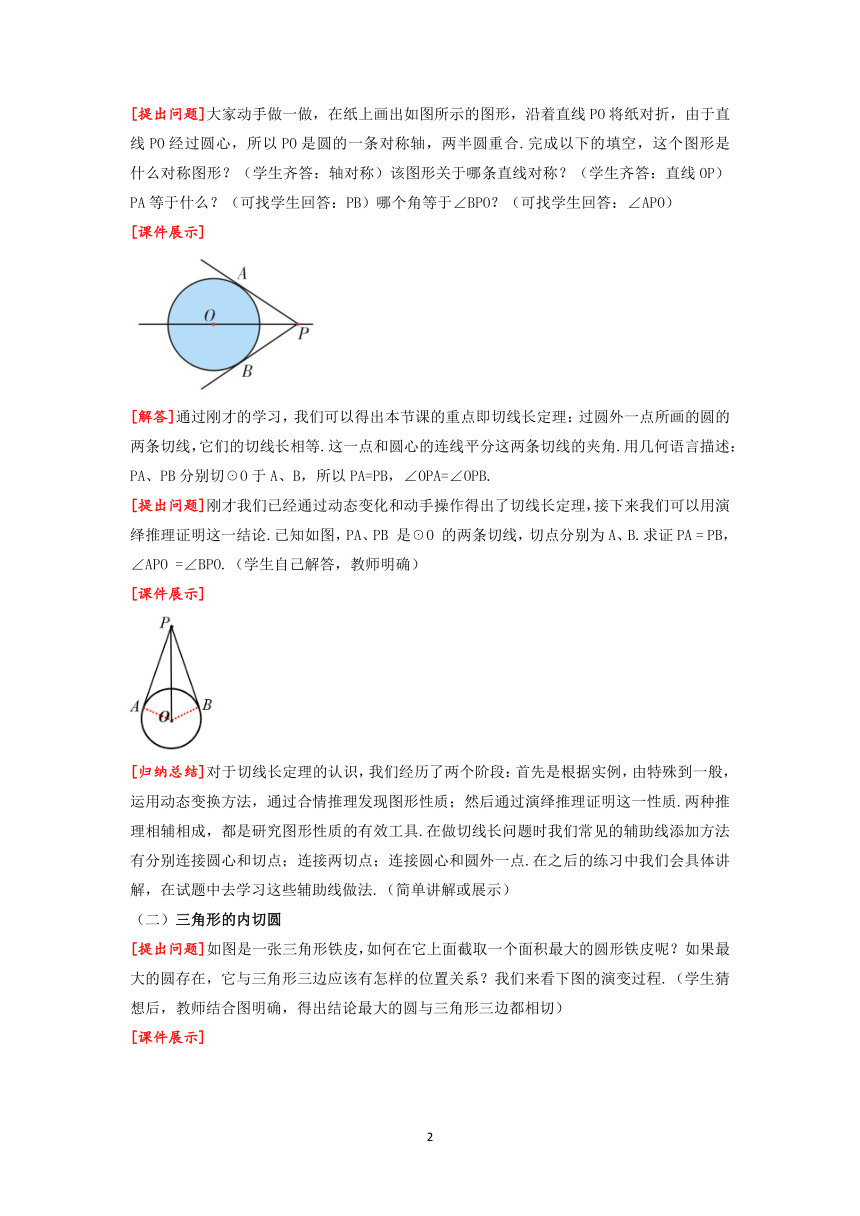
[提出问题]大家动手做一做,在纸上画出如图所示的图形,沿着直线PO将纸对折,由于直线PO经过圆心,所以PO是圆的一条对称轴,两半圆重合.完成以下的填空,这个图形是 什么对称图形?(学生齐答:轴对称)该图形关于哪条直线对称?(学生齐答:直线OP)PA等于什么?(可找学生回答:PB)哪个角等于∠BPO?(可找学生回答:∠APO)
[课件展示]
[解答]通过刚才的学习,我们可以得出本节课的重点即切线长定理:过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.用几何语言描述:PA、PB分别切☉O于A、B,所以PA=PB,∠OPA=∠OPB.
[提出问题]刚才我们已经通过动态变化和动手操作得出了切线长定理,接下来我们可以用演绎推理证明这一结论.已知如图,PA、PB 是☉O 的两条切线,切点分别为A、B.求证PA = PB,∠APO =∠BPO.(学生自己解答,教师明确)
[课件展示]
[归纳总结]对于切线长定理的认识,我们经历了两个阶段:首先是根据实例,由特殊到一般,运用动态变换方法,通过合情推理发现图形性质;然后通过演绎推理证明这一性质.两种推理相辅相成,都是研究图形性质的有效工具.在做切线长问题时我们常见的辅助线添加方法有分别连接圆心和切点;连接两切点;连接圆心和圆外一点.在之后的练习中我们会具体讲解,在试题中去学习这些辅助线做法.(简单讲解或展示)
三角形的内切圆
[提出问题]如图是一张三角形铁皮,如何在它上面截取一个面积最大的圆形铁皮呢?如果最大的圆存在,它与三角形三边应该有怎样的位置关系?我们来看下图的演变过程.(学生猜想后,教师结合图明确,得出结论最大的圆与三角形三边都相切)
[课件展示]
[提出问题]若已知△ABC,我们怎么作出和△ABC的各边都相切的圆O?
[解答](结合图示讲解)作法:首先作∠ABC和∠ACB的平分线BM和CN,交点为O;接着过点O作OD⊥BC,垂足为D;然后以O为圆心,OD为半径作圆O,则☉O就是所求的圆.
[课件展示]
[解答]通过作图我们得到如下定义,与三角形各边都相切的圆叫做这个三角形的内切圆.三角形的内切圆的圆心叫做这个三角形的内心.这个三角形叫做这个圆的外切三角形.通过图片我们可以说△ABC的内切圆是☉I,△ABC 的内心是点 I,☉I的外切三角形是△ABC.
[课件展示]
[提出问题]通过学习三角形的内切圆,我们还可以得出哪些结论?如图,☉I是△ABC的内切圆,那么AI、BI、CI有什么特点?(学生回答,教师明确AI、BI、CI分别平分∠CAB、∠ABC、∠BCA)如图,分别过点作 AB、AC、BC 的垂线,垂足分别为 E、F,G,那么线段 IE、IF、IG之间有什么关系?(学生回答,教师明确IE=IF=IG)
[课件展示]
[解答]通过学习,我们可以得到三角形内心的性质:第一三角形的内心在三角形的角平分线上;第二三角形的内心到三角形的三边距离相等.通过图示可表述为AI、BI、CI分别平分
∠CAB、∠ABC、∠BCA,IE=IF=IG.
[提出问题]外心和内心比较容易混淆,我们通过表格和作图来对比一下,帮助大家更好地梳理这部分知识.首先三角形的外心是什么?(三角形外接圆的圆心),三角形的内心又是什么?(三角形内切圆的圆心)外心如何确定?(三角形三边中垂线的交点)内心如何确定?(三角形三条角平分线的交点)由外心我们可以得到哪些性质?(1.OA = OB = OC;
2. 外心不一定在三角形的内部.)由内心我们可以得到哪些性质?(1.到三边的距离相等;
2. OA、OB、OC 分别平分∠BAC、∠ABC、∠ACB;3. 内心在三角形内部.)
[归纳总结]今天我们学习了圆中重要的切线长定理,然后学习了三角形的内切圆,并对容易混淆的知识进行对比复习.
【课堂小结】
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
圆
27.2 与圆有关的位置关系
3. 切线
第2课时 切线长定理及三角形的内切圆
1.切线长定理
2.三角形的内切圆
【教学反思】
一、案例的“亮点”
1.通过同学们在抖空竹时,当同学们把篮球夹在胳膊中,当同学们在玩悠悠球时,抽象出本节课学习的重点模型直线与圆相切的位置关系到切线长定理模型,引出切线长定理.对于切线长定理的认识,经历了两个阶段:首先是根据实例,由特殊到一般,运用动态变换方法,通过合情推理发现图形性质;然后通过演绎推理证明这一性质.两种推理相辅相成,都是研究图形性质的有效工具,并总结了常见的辅助线的作图方法.这样可以使学生增加学习的兴趣,并且层层递进总结,方便学生循序渐进,巩固新知.
2. 教学过程中,强调用切线长定理可解决有关求角度、周长的问题.明确三角形内切圆的圆心是三角形三条角平分线的交点,到三边的距离相等.
3.对内切圆,外切圆,内心和外心等较难且易混的知识点讲解详细且让学生对比识记,强化学生对易混知识的理解.
二、教学中易出现的问题
学生小组讨论或解题的过程中,注意学生是否参与到问题的探究中,总结知识点的过程中注意对学生的引导,让学生自己能够总结出相应的答案、结论与定义.教学过程中,强调学生从实际生活中感受,体会切线长定理,并会用几何语言来描述归纳,经历将实际问题转化为数学问题的过程,即数形结合思想的感受与理解.因为各部分知识点联系紧密,所以教师要时刻关注学生学习掌握的情况,及时解决探究过程中学生遇到的各种问题,使学生扎实全面的掌握知识.
27.2 与圆有关的位置关系
3.切线
第2课时 切线长定理及三角形的内切圆
一、教学目标
1.理解并掌握切线长定理;
2.了解三角形的内心、内切圆及外切三角形的概念.
二、教学重难点
重点:掌握切线长定理,初步学会运用切线长定理进行计算与证明
难点:了解有关三角形的内切圆和三角形的内心的概念
【新课导入】
[提出问题]看课件上的图片,当同学们在抖空竹时,当同学们把篮球夹在胳膊中,当同学们在玩悠悠球时,如图所示的时刻的情景,你能从中抽象出什么样的数学图形?(教师展示图片,学生描述后展示图片中的数学图形)
[课件展示]
[过渡]从图中的模型可以看出为一个圆和两条切线,本节课我们就来学习这个模型及和圆的切线有关的知识.
【新知探究】
切线长定理
[提出问题]从圆外一点引圆的切线,最多能作出几条切线?(展示图片,教师明确2条)
这一点和切点之间的线段的长叫做切线长.
[课件展示]
[解答]这一点和切点之间的线段的长叫做切线长.
[提出问题]切线和切线长是一个意思吗?
[解答]切线和切线长是两个不同的概念:切线是一条与圆相切的直线,不能度量,而切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.二者的联系是都垂直于过切点的半径.
[提出问题]大家动手做一做,在纸上画出如图所示的图形,沿着直线PO将纸对折,由于直线PO经过圆心,所以PO是圆的一条对称轴,两半圆重合.完成以下的填空,这个图形是 什么对称图形?(学生齐答:轴对称)该图形关于哪条直线对称?(学生齐答:直线OP)PA等于什么?(可找学生回答:PB)哪个角等于∠BPO?(可找学生回答:∠APO)
[课件展示]
[解答]通过刚才的学习,我们可以得出本节课的重点即切线长定理:过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.用几何语言描述:PA、PB分别切☉O于A、B,所以PA=PB,∠OPA=∠OPB.
[提出问题]刚才我们已经通过动态变化和动手操作得出了切线长定理,接下来我们可以用演绎推理证明这一结论.已知如图,PA、PB 是☉O 的两条切线,切点分别为A、B.求证PA = PB,∠APO =∠BPO.(学生自己解答,教师明确)
[课件展示]
[归纳总结]对于切线长定理的认识,我们经历了两个阶段:首先是根据实例,由特殊到一般,运用动态变换方法,通过合情推理发现图形性质;然后通过演绎推理证明这一性质.两种推理相辅相成,都是研究图形性质的有效工具.在做切线长问题时我们常见的辅助线添加方法有分别连接圆心和切点;连接两切点;连接圆心和圆外一点.在之后的练习中我们会具体讲解,在试题中去学习这些辅助线做法.(简单讲解或展示)
三角形的内切圆
[提出问题]如图是一张三角形铁皮,如何在它上面截取一个面积最大的圆形铁皮呢?如果最大的圆存在,它与三角形三边应该有怎样的位置关系?我们来看下图的演变过程.(学生猜想后,教师结合图明确,得出结论最大的圆与三角形三边都相切)
[课件展示]
[提出问题]若已知△ABC,我们怎么作出和△ABC的各边都相切的圆O?
[解答](结合图示讲解)作法:首先作∠ABC和∠ACB的平分线BM和CN,交点为O;接着过点O作OD⊥BC,垂足为D;然后以O为圆心,OD为半径作圆O,则☉O就是所求的圆.
[课件展示]
[解答]通过作图我们得到如下定义,与三角形各边都相切的圆叫做这个三角形的内切圆.三角形的内切圆的圆心叫做这个三角形的内心.这个三角形叫做这个圆的外切三角形.通过图片我们可以说△ABC的内切圆是☉I,△ABC 的内心是点 I,☉I的外切三角形是△ABC.
[课件展示]
[提出问题]通过学习三角形的内切圆,我们还可以得出哪些结论?如图,☉I是△ABC的内切圆,那么AI、BI、CI有什么特点?(学生回答,教师明确AI、BI、CI分别平分∠CAB、∠ABC、∠BCA)如图,分别过点作 AB、AC、BC 的垂线,垂足分别为 E、F,G,那么线段 IE、IF、IG之间有什么关系?(学生回答,教师明确IE=IF=IG)
[课件展示]
[解答]通过学习,我们可以得到三角形内心的性质:第一三角形的内心在三角形的角平分线上;第二三角形的内心到三角形的三边距离相等.通过图示可表述为AI、BI、CI分别平分
∠CAB、∠ABC、∠BCA,IE=IF=IG.
[提出问题]外心和内心比较容易混淆,我们通过表格和作图来对比一下,帮助大家更好地梳理这部分知识.首先三角形的外心是什么?(三角形外接圆的圆心),三角形的内心又是什么?(三角形内切圆的圆心)外心如何确定?(三角形三边中垂线的交点)内心如何确定?(三角形三条角平分线的交点)由外心我们可以得到哪些性质?(1.OA = OB = OC;
2. 外心不一定在三角形的内部.)由内心我们可以得到哪些性质?(1.到三边的距离相等;
2. OA、OB、OC 分别平分∠BAC、∠ABC、∠ACB;3. 内心在三角形内部.)
[归纳总结]今天我们学习了圆中重要的切线长定理,然后学习了三角形的内切圆,并对容易混淆的知识进行对比复习.
【课堂小结】
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
圆
27.2 与圆有关的位置关系
3. 切线
第2课时 切线长定理及三角形的内切圆
1.切线长定理
2.三角形的内切圆
【教学反思】
一、案例的“亮点”
1.通过同学们在抖空竹时,当同学们把篮球夹在胳膊中,当同学们在玩悠悠球时,抽象出本节课学习的重点模型直线与圆相切的位置关系到切线长定理模型,引出切线长定理.对于切线长定理的认识,经历了两个阶段:首先是根据实例,由特殊到一般,运用动态变换方法,通过合情推理发现图形性质;然后通过演绎推理证明这一性质.两种推理相辅相成,都是研究图形性质的有效工具,并总结了常见的辅助线的作图方法.这样可以使学生增加学习的兴趣,并且层层递进总结,方便学生循序渐进,巩固新知.
2. 教学过程中,强调用切线长定理可解决有关求角度、周长的问题.明确三角形内切圆的圆心是三角形三条角平分线的交点,到三边的距离相等.
3.对内切圆,外切圆,内心和外心等较难且易混的知识点讲解详细且让学生对比识记,强化学生对易混知识的理解.
二、教学中易出现的问题
学生小组讨论或解题的过程中,注意学生是否参与到问题的探究中,总结知识点的过程中注意对学生的引导,让学生自己能够总结出相应的答案、结论与定义.教学过程中,强调学生从实际生活中感受,体会切线长定理,并会用几何语言来描述归纳,经历将实际问题转化为数学问题的过程,即数形结合思想的感受与理解.因为各部分知识点联系紧密,所以教师要时刻关注学生学习掌握的情况,及时解决探究过程中学生遇到的各种问题,使学生扎实全面的掌握知识.
