27.4 正多边形和圆 教案 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.4 正多边形和圆 教案 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 17:22:44 | ||
图片预览


文档简介
第27章 圆
27.4 正多边形和圆
一、教学目标
1.掌握正多边形和圆的关系;
2.理解正多边形的中心、半径、中心角、边心距等概念;
3.能运用正多边形的知识解决圆的有关计算问题;
4.会运用多边形知和圆的有关知识画多边形.
二、教学重难点
重点:掌握圆内接正多边形的半径和边长、边心距、中心角之间的关系
难点:掌握圆内接正多边形的画法
【新课导入】
观察这些美丽的图形和生活中的多边形,这节课我们就来学习圆和多边形.
[课件展示]
【新知探究】
正多边形与圆的关系
[提出问题]各边相等,各角也相等的多边形叫做正多边形.如果只说各边相等的多边形是正多边形对吗?为什么?只说各角相等的多边形是正多边形对吗?为什么?
[解答]各边相等的多边形是正多边形不对,如菱形;各角相等的多边形是正多边形不对,如矩形.
[提出问题]接下来我们继续探究,思考一下,分别画出下图各正多边形的对称轴,看看能发现什么结果?
[课件展示]
[解答]通过图片我们可以归纳总结:正n边形都是轴对称图形,都有n条对称轴,而且只有边数为偶数的正多边形才是中心对称图形.
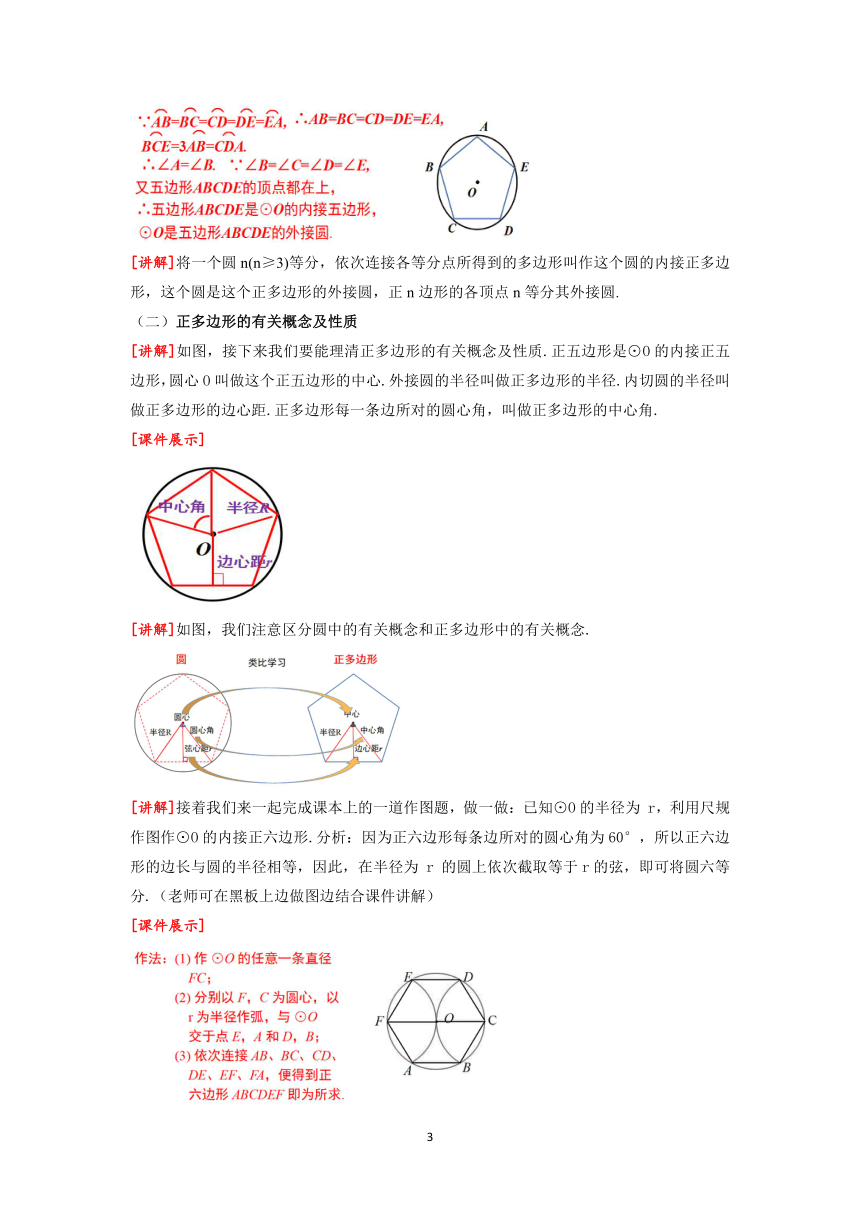
[解答]接下来我们继续学习和正多边形有关的知识,如图,顶点都在同一圆上的正多边形叫做圆内接正多边形.这个圆叫做该正多边形的外接圆.
[课件展示]
[提出问题]正五边形有几个外接圆和几个内切圆呢?以正五边形为例,观察正五边形与圆有何关系?
[课件展示]
[提出问题]我们一起来完成以下问题,如图,正五边形的对称轴都交于一点O.这些对称轴是正五边形各边的什么(学生回答,教师明确垂直平分线),故点O到正五边形各个 什么(学生齐答:边)的距离相等,记为R.以点O为圆心、R为半径的圆就过正五边形的各个顶点,即为正五边形的外接圆;这些对称轴也是正五边形各内角的什么(学生回答,角平分线),故点O到正五边形各什么(学生齐答:边)的距离都相等,记为r.以点O为圆心、r为半径的圆就与正五边形的各条边都相切,即为正五边形的内切圆.
[提出问题]通过刚才的学习我们可以得出结论:正五边形有且只有一个外接圆和一个内切圆,那么其他的正多边形是否一样呢?如图,作出下列正多边形的外接圆和内切圆,从中你能发现什么?
[课件展示]
[解答]对于刚才的问题,通过学习,我们可以得出归纳总结:任何正多边形都有一个外接圆和一个内切圆.
[解答]以证明题我们继续,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.以圆的内接正五边形为例证明.(讲解例题)
[课件展示]
[讲解]将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正n边形的各顶点n等分其外接圆.
正多边形的有关概念及性质
[讲解]如图,接下来我们要能理清正多边形的有关概念及性质.正五边形是⊙O的内接正五边形,圆心O叫做这个正五边形的中心.外接圆的半径叫做正多边形的半径.内切圆的半径叫做正多边形的边心距.正多边形每一条边所对的圆心角,叫做正多边形的中心角.
[课件展示]
[讲解]如图,我们注意区分圆中的有关概念和正多边形中的有关概念.
[讲解]接着我们来一起完成课本上的一道作图题,做一做:已知⊙O的半径为 r,利用尺规作图作⊙O的内接正六边形.分析:因为正六边形每条边所对的圆心角为60°,所以正六边形的边长与圆的半径相等,因此,在半径为 r 的圆上依次截取等于r的弦,即可将圆六等分.(老师可在黑板上边做图边结合课件讲解)
[课件展示]
[提出问题]请大家按课本步骤自己尝试完成利用尺规作图作出已知圆的内接正方形.(教师可让学生在黑板上作图,其余同学演草纸上作图,然后教师在黑板上明确)
[过渡]我们学习了圆内接正多边形的有关概念,接下来我们学习与其有关的计算.
圆内接正多边形的有关计算
[提出问题]请同学们讨论,完成下面的5道填空题.(找同学回答,教师明确)
[课件展示]
[提出问题]通过刚才大家的自主学习,总结出了每道题的答案,接下来我们练习一道例题检验一下我们刚才总结的答案.(同学解答,教师明确)
[课件展示]
[归纳总结]本节课我们学习了圆内接正多边形,我们先讲了正多边形和圆的关系,然后讲了和正多边形有关的概念(中心、半径、边心距、中心角),最后我们讲了正多边形的有关计算,在下课前我们在一起来复习一遍.(此部分老师可以再次打乱顺序提问,找学生回答或学生齐答作总结复习).
【课堂小结】
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
圆
27.4 正多边形和圆
正多边形和圆的关系
正多边形的有关概念及性质
3.圆内接正多边形的有关计算
【教学反思】
一、案例的“亮点”
1.本节课通过生活中美丽的图案和常见的多边形图形作为导入,让课堂丰富多彩,增加课堂学习的兴趣.
2.本节课新的概念比较多,对概念的教学从“形”的角度去认识和辨析,但对概念的严格定义要求以理解为主.在概念教学中,重视运用启发式教学,让学生从“形”的特征中自己总结获得对几何概念的直观认识,鼓励学生自己总结探索并能自己阐述有关概念,再进一步准确理解有关概念的文字表述,通过习题加深对概念的结合运用.
3.积极与学生互动,方式多样且较为灵活,在结课时可以通过提问复习的形式作为收束.
二、教学中易出现的问题
注意区分圆中的有关概念和正多边形中的有关概念,提醒学生容易混淆的地方,区分清楚圆的内接正多边形和正多边形的外接圆;本节课教师应注重在黑板上结合画图讲解或证明等,使学生更直观的理解问题.
27.4 正多边形和圆
一、教学目标
1.掌握正多边形和圆的关系;
2.理解正多边形的中心、半径、中心角、边心距等概念;
3.能运用正多边形的知识解决圆的有关计算问题;
4.会运用多边形知和圆的有关知识画多边形.
二、教学重难点
重点:掌握圆内接正多边形的半径和边长、边心距、中心角之间的关系
难点:掌握圆内接正多边形的画法
【新课导入】
观察这些美丽的图形和生活中的多边形,这节课我们就来学习圆和多边形.
[课件展示]
【新知探究】
正多边形与圆的关系
[提出问题]各边相等,各角也相等的多边形叫做正多边形.如果只说各边相等的多边形是正多边形对吗?为什么?只说各角相等的多边形是正多边形对吗?为什么?
[解答]各边相等的多边形是正多边形不对,如菱形;各角相等的多边形是正多边形不对,如矩形.
[提出问题]接下来我们继续探究,思考一下,分别画出下图各正多边形的对称轴,看看能发现什么结果?
[课件展示]
[解答]通过图片我们可以归纳总结:正n边形都是轴对称图形,都有n条对称轴,而且只有边数为偶数的正多边形才是中心对称图形.
[解答]接下来我们继续学习和正多边形有关的知识,如图,顶点都在同一圆上的正多边形叫做圆内接正多边形.这个圆叫做该正多边形的外接圆.
[课件展示]
[提出问题]正五边形有几个外接圆和几个内切圆呢?以正五边形为例,观察正五边形与圆有何关系?
[课件展示]
[提出问题]我们一起来完成以下问题,如图,正五边形的对称轴都交于一点O.这些对称轴是正五边形各边的什么(学生回答,教师明确垂直平分线),故点O到正五边形各个 什么(学生齐答:边)的距离相等,记为R.以点O为圆心、R为半径的圆就过正五边形的各个顶点,即为正五边形的外接圆;这些对称轴也是正五边形各内角的什么(学生回答,角平分线),故点O到正五边形各什么(学生齐答:边)的距离都相等,记为r.以点O为圆心、r为半径的圆就与正五边形的各条边都相切,即为正五边形的内切圆.
[提出问题]通过刚才的学习我们可以得出结论:正五边形有且只有一个外接圆和一个内切圆,那么其他的正多边形是否一样呢?如图,作出下列正多边形的外接圆和内切圆,从中你能发现什么?
[课件展示]
[解答]对于刚才的问题,通过学习,我们可以得出归纳总结:任何正多边形都有一个外接圆和一个内切圆.
[解答]以证明题我们继续,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.以圆的内接正五边形为例证明.(讲解例题)
[课件展示]
[讲解]将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正n边形的各顶点n等分其外接圆.
正多边形的有关概念及性质
[讲解]如图,接下来我们要能理清正多边形的有关概念及性质.正五边形是⊙O的内接正五边形,圆心O叫做这个正五边形的中心.外接圆的半径叫做正多边形的半径.内切圆的半径叫做正多边形的边心距.正多边形每一条边所对的圆心角,叫做正多边形的中心角.
[课件展示]
[讲解]如图,我们注意区分圆中的有关概念和正多边形中的有关概念.
[讲解]接着我们来一起完成课本上的一道作图题,做一做:已知⊙O的半径为 r,利用尺规作图作⊙O的内接正六边形.分析:因为正六边形每条边所对的圆心角为60°,所以正六边形的边长与圆的半径相等,因此,在半径为 r 的圆上依次截取等于r的弦,即可将圆六等分.(老师可在黑板上边做图边结合课件讲解)
[课件展示]
[提出问题]请大家按课本步骤自己尝试完成利用尺规作图作出已知圆的内接正方形.(教师可让学生在黑板上作图,其余同学演草纸上作图,然后教师在黑板上明确)
[过渡]我们学习了圆内接正多边形的有关概念,接下来我们学习与其有关的计算.
圆内接正多边形的有关计算
[提出问题]请同学们讨论,完成下面的5道填空题.(找同学回答,教师明确)
[课件展示]
[提出问题]通过刚才大家的自主学习,总结出了每道题的答案,接下来我们练习一道例题检验一下我们刚才总结的答案.(同学解答,教师明确)
[课件展示]
[归纳总结]本节课我们学习了圆内接正多边形,我们先讲了正多边形和圆的关系,然后讲了和正多边形有关的概念(中心、半径、边心距、中心角),最后我们讲了正多边形的有关计算,在下课前我们在一起来复习一遍.(此部分老师可以再次打乱顺序提问,找学生回答或学生齐答作总结复习).
【课堂小结】
【课堂训练】学生完成本课时PPT练习题,教师讲评.
【布置作业】
【板书设计】
圆
27.4 正多边形和圆
正多边形和圆的关系
正多边形的有关概念及性质
3.圆内接正多边形的有关计算
【教学反思】
一、案例的“亮点”
1.本节课通过生活中美丽的图案和常见的多边形图形作为导入,让课堂丰富多彩,增加课堂学习的兴趣.
2.本节课新的概念比较多,对概念的教学从“形”的角度去认识和辨析,但对概念的严格定义要求以理解为主.在概念教学中,重视运用启发式教学,让学生从“形”的特征中自己总结获得对几何概念的直观认识,鼓励学生自己总结探索并能自己阐述有关概念,再进一步准确理解有关概念的文字表述,通过习题加深对概念的结合运用.
3.积极与学生互动,方式多样且较为灵活,在结课时可以通过提问复习的形式作为收束.
二、教学中易出现的问题
注意区分圆中的有关概念和正多边形中的有关概念,提醒学生容易混淆的地方,区分清楚圆的内接正多边形和正多边形的外接圆;本节课教师应注重在黑板上结合画图讲解或证明等,使学生更直观的理解问题.
