27.1.2 第1课时 圆心角、弧、弦之间的关系 课件(共17张PPT)2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.1.2 第1课时 圆心角、弧、弦之间的关系 课件(共17张PPT)2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 17:32:49 | ||
图片预览



文档简介
(共17张PPT)
第27章 圆
27.1 圆的认识
2.圆的对称性
第1课时 圆心角、弧、弦之间的关系
华师大版-数学-九年级下册
学习目标
1.理解圆的对称性,知道圆既是旋转对称图形,又是轴对称图形,能说出圆的对称轴和对称中心.
【重点】掌握圆心角、弧、弦之间的关系,并能利用其解决相关问题.
【难点】探索圆的对称性及其相关性质.
2.探索圆心角、弧、弦之间的关系,并利用其解决问题.
新课导入
观察摩天轮的旋转过程,你有什么发现?
新知探究
问题1:
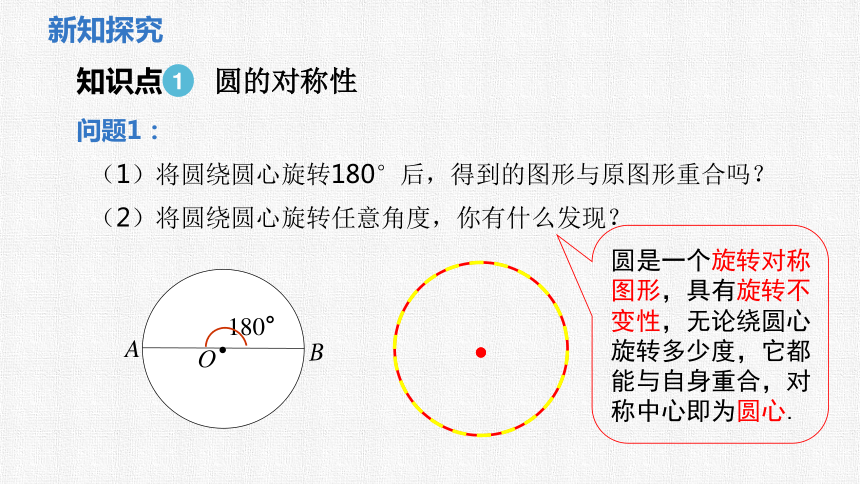
(1)将圆绕圆心旋转180°后,得到的图形与原图形重合吗?
.
O
A
B
180°
(2)将圆绕圆心旋转任意角度,你有什么发现?
·
圆是一个旋转对称图形,具有旋转不变性,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为圆心.
知识点 圆的对称性
1
新知探究
问题2:
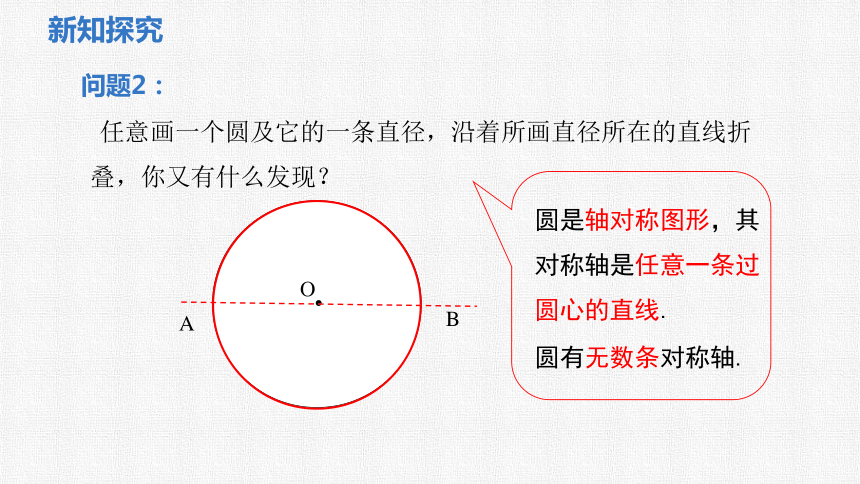
任意画一个圆及它的一条直径,沿着所画直径所在的直线折叠,你又有什么发现?
.
O
A
B
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
圆有无数条对称轴.
新知探究
O
A
B
C
C'
A'
B'
在同圆中探究
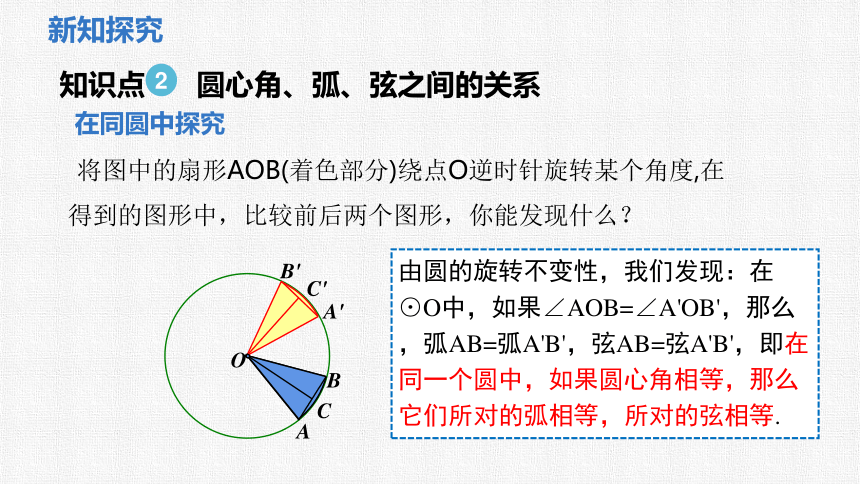
将图中的扇形AOB(着色部分)绕点O逆时针旋转某个角度,在得到的图形中,比较前后两个图形,你能发现什么?
由圆的旋转不变性,我们发现:在⊙O中,如果∠AOB=∠A'OB',那么,弧AB=弧A'B',弦AB=弦A'B',即在同一个圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
知识点 圆心角、弧、弦之间的关系
2
新知探究
在等圆中探究
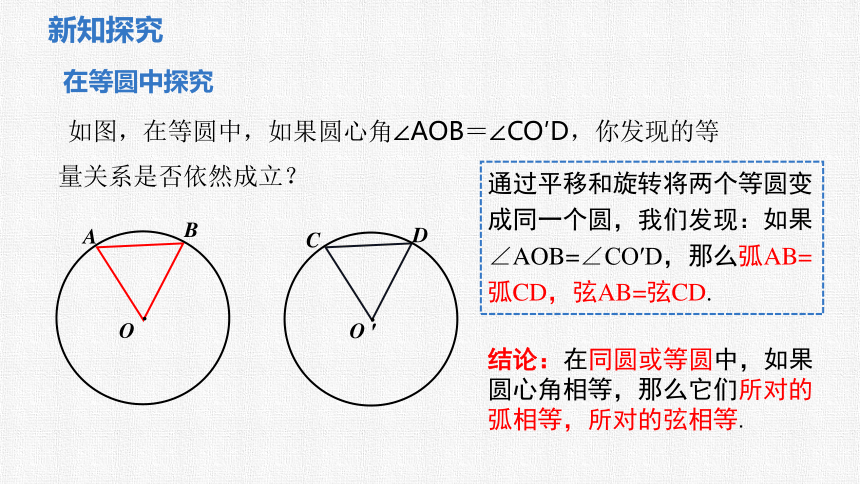
如图,在等圆中,如果圆心角∠AOB=∠CO′D,你发现的等量关系是否依然成立?
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO′D,那么弧AB=弧CD,弦AB=弦CD.
O ′
·
O
A
B
·
C
D
结论:在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
新知探究
A
B
O
D
C
想一想:
定理“在同一个圆中,如果圆心角相等,那么它们所对弧相等,所对的弦相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
新知探究
在同圆或等圆中
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
题设
结论
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
弧、弦与圆心角的关系推论
新知探究
在同圆或等圆中
A
B
O
D
C
圆心角相等
(∠AOB=∠COD)
弦相等
(AB=CD)
弧相等
( )
AB=CD
(
(
关系结构图
课堂小结
一、圆的对称性
1.圆是旋转对称图形,对称中心是其圆心.圆具有旋转不变性,一个圆绕它的圆心旋转任意角度,都能与原来的图形重合.
二、圆心角、弧、弦之间的关系
1.在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
2.圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴.
2.在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
3.在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
课堂训练
1.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形
B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴
D.圆的对称中心是它的圆心
B
课堂训练
2.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.在同圆中,圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
C
3.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_______________.
(2)如果 ,那么____________,__________________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
O
AB=CD
(
(
AB=CD
AB=CD
AB=CD
(
(
∠AOB= ∠COD
∠AOB= ∠COD
AB=CD
(
(
课堂训练
新知探究
4.如图,在⊙O中,AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
证明:
∴ AB=AC,△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
∵AB=AC,
⌒ ⌒
A
B
C
O
⌒ ⌒
课堂训练
5.如图, AB是⊙O的直径,C、D是BE的三等分点,∠AOE=60°,则∠COE的度数是( )
A. 40° B. 60°
C. 80° D. 120°
C
O
A
B
C
D
E
(
课堂训练
6.如图,在⊙O中,AB、CD是直径,CE∥AB且交圆于点E,
求证:BD=BE.
(
(
证明:
如图,连接OE.
∵CE∥AB,
∴∠DOB=∠C,∠BOE=∠E.
(
(
∴∠DOB=∠BOE,∴BD=BE.
(
(
第27章 圆
27.1 圆的认识
2.圆的对称性
第1课时 圆心角、弧、弦之间的关系
华师大版-数学-九年级下册
学习目标
1.理解圆的对称性,知道圆既是旋转对称图形,又是轴对称图形,能说出圆的对称轴和对称中心.
【重点】掌握圆心角、弧、弦之间的关系,并能利用其解决相关问题.
【难点】探索圆的对称性及其相关性质.
2.探索圆心角、弧、弦之间的关系,并利用其解决问题.
新课导入
观察摩天轮的旋转过程,你有什么发现?
新知探究
问题1:
(1)将圆绕圆心旋转180°后,得到的图形与原图形重合吗?
.
O
A
B
180°
(2)将圆绕圆心旋转任意角度,你有什么发现?
·
圆是一个旋转对称图形,具有旋转不变性,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为圆心.
知识点 圆的对称性
1
新知探究
问题2:
任意画一个圆及它的一条直径,沿着所画直径所在的直线折叠,你又有什么发现?
.
O
A
B
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
圆有无数条对称轴.
新知探究
O
A
B
C
C'
A'
B'
在同圆中探究
将图中的扇形AOB(着色部分)绕点O逆时针旋转某个角度,在得到的图形中,比较前后两个图形,你能发现什么?
由圆的旋转不变性,我们发现:在⊙O中,如果∠AOB=∠A'OB',那么,弧AB=弧A'B',弦AB=弦A'B',即在同一个圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
知识点 圆心角、弧、弦之间的关系
2
新知探究
在等圆中探究
如图,在等圆中,如果圆心角∠AOB=∠CO′D,你发现的等量关系是否依然成立?
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠CO′D,那么弧AB=弧CD,弦AB=弦CD.
O ′
·
O
A
B
·
C
D
结论:在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
新知探究
A
B
O
D
C
想一想:
定理“在同一个圆中,如果圆心角相等,那么它们所对弧相等,所对的弦相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
新知探究
在同圆或等圆中
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
题设
结论
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
弧、弦与圆心角的关系推论
新知探究
在同圆或等圆中
A
B
O
D
C
圆心角相等
(∠AOB=∠COD)
弦相等
(AB=CD)
弧相等
( )
AB=CD
(
(
关系结构图
课堂小结
一、圆的对称性
1.圆是旋转对称图形,对称中心是其圆心.圆具有旋转不变性,一个圆绕它的圆心旋转任意角度,都能与原来的图形重合.
二、圆心角、弧、弦之间的关系
1.在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦相等.
2.圆是轴对称图形,它的任意一条直径所在的直线都是它的对称轴.
2.在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等,所对的弦相等.
3.在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等,所对的弧相等.
课堂训练
1.下列说法中,不正确的是( )
A.圆既是轴对称图形又是中心对称图形
B.圆的每一条直径都是它的对称轴
C.圆有无数条对称轴
D.圆的对称中心是它的圆心
B
课堂训练
2.下列说法中,正确的是( )
A.等弦所对的弧相等
B.等弧所对的弦相等
C.在同圆中,圆心角相等,所对的弦相等
D.弦相等,所对的圆心角相等
C
3.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_______________.
(2)如果 ,那么____________,__________________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
O
AB=CD
(
(
AB=CD
AB=CD
AB=CD
(
(
∠AOB= ∠COD
∠AOB= ∠COD
AB=CD
(
(
课堂训练
新知探究
4.如图,在⊙O中,AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
证明:
∴ AB=AC,△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
∵AB=AC,
⌒ ⌒
A
B
C
O
⌒ ⌒
课堂训练
5.如图, AB是⊙O的直径,C、D是BE的三等分点,∠AOE=60°,则∠COE的度数是( )
A. 40° B. 60°
C. 80° D. 120°
C
O
A
B
C
D
E
(
课堂训练
6.如图,在⊙O中,AB、CD是直径,CE∥AB且交圆于点E,
求证:BD=BE.
(
(
证明:
如图,连接OE.
∵CE∥AB,
∴∠DOB=∠C,∠BOE=∠E.
(
(
∴∠DOB=∠BOE,∴BD=BE.
(
(
