27.1.3 第2课时 圆周角定理的推论 课件(共19张PPT)2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.1.3 第2课时 圆周角定理的推论 课件(共19张PPT)2024-2025学年数学华东师大版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 453.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 17:33:51 | ||
图片预览




文档简介
(共19张PPT)
第27章 圆
27.1 圆的认识
3.圆周角
第2课时 圆周角定理的推论
华师大版-数学-九年级下册
学习目标
1.能够理解和掌握圆周角定理的推论;
【重点】能运用圆周角定理的推论解决简单的证明或计算.【难点】理解掌握圆周角定理的推论及其证明过程和运用.
2.了解圆周角和直径的关系以及圆内接四边形的概念.
新课导入
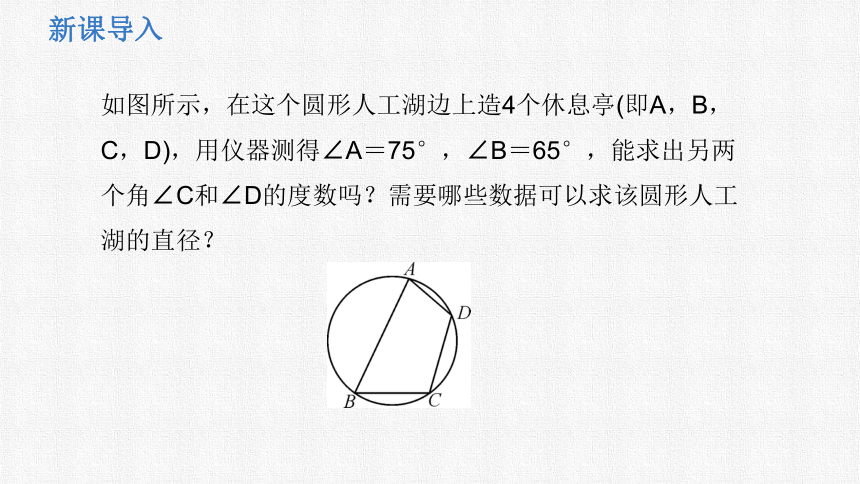
如图所示,在这个圆形人工湖边上造4个休息亭(即A,B,C,D),用仪器测得∠A=75°,∠B=65°,能求出另两个角∠C和∠D的度数吗?需要哪些数据可以求该圆形人工湖的直径?
新知探究
问题 上一课时我们证明了半圆或直径所对的圆周角都是90°,那么反过来,如图,圆周角∠BAC=90°,弦BC是直径吗 为什么
解:连结OB,OC,
∵圆周角∠BAC=90°,
∴圆心角∠BOC=180°,即BOC是一条线段,
∴BC是☉O的一条直径.
圆周角定理的推论1 90°的圆周角所对的弦是直径.
知识点 圆周角定理的推论1
1
新知探究
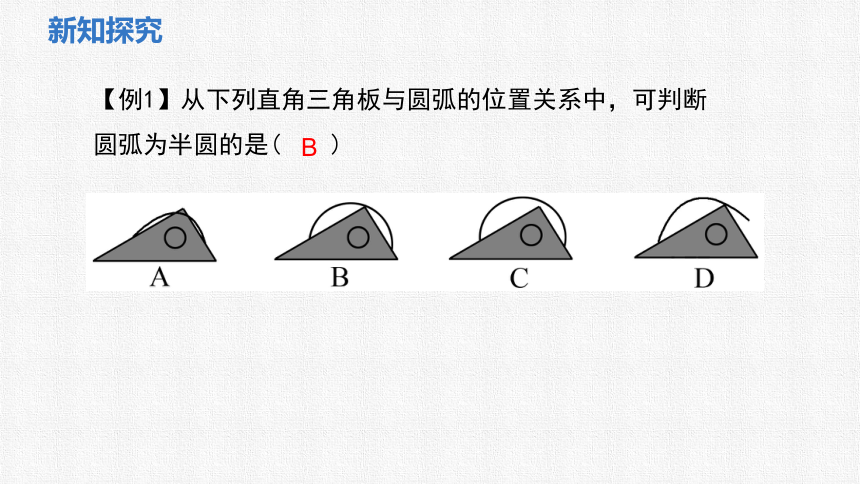
【例1】从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
B
新知探究
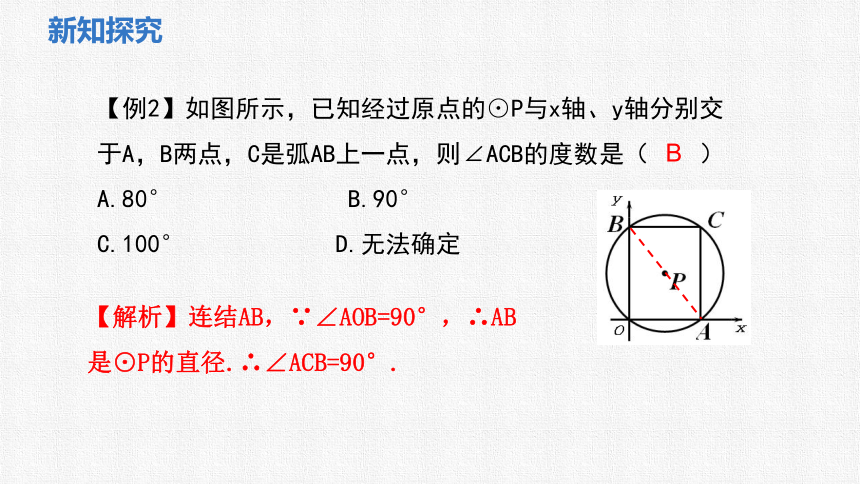
【例2】如图所示,已知经过原点的⊙P与x轴、y轴分别交于A,B两点,C是弧AB上一点,则∠ACB的度数是( )
A.80° B.90°
C.100° D.无法确定
B
【解析】连结AB,∵∠AOB=90°,∴AB是⊙P的直径.∴∠ACB=90°.
新知探究
总 结
1.有直径,通常作直径所对的圆周角,从而得出两直线互相垂直,简记为“见直径作直角 ”.
2.有90°的圆周角,通常作直径,简记为“有直角作直径”.
新知探究
1.圆内接多边形
定义:如果一个圆经过一个多边形的各个顶点,这个圆就叫做这个多边形的外接圆,这个多边形叫做这个圆的内接多边形.
圆内接四边形有什么性质呢?
知识点 圆周角定理的推论2
2
新知探究
2.圆周角定理的推论2
问题1 如图,A,B,C,D是☉O上的四点,AC为☉O的直径,请问∠BAD与∠BCD之间有什么关系
解:∵AC为☉O的直径,
∴∠ADC=∠ABC=90°,
∴∠BAD+∠BCD=180°.
新知探究
问题2 在☉O上移动点C,如图,∠BAD与∠BCD之间的关系还成立吗
解:∵优弧BCD和劣弧BAD的度数和为360°
那么它们所对的圆心角的和也是360°,
即∠BAD+∠BCD=180°.
∴它们所对的圆周角∠BAD和∠BCD的和是180°,
圆周角定理的推论2 圆内接四边形的对角互补.
新知探究
【例3】四边形ABCD是⊙O的内接四边形,且∠A=110°,∠B=80°,则∠C= ,∠D= .
70°
100°
新知探究
【例4】如图,四边形ABCD内接于⊙O,点E是CB的延长线上一点,∠EBA=125°,则∠D=( )
A.65° B.120° C.125° D.130°
C
新知探究
【例5】在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰4.求这个四边形各角的度数.
解:设∠A,∠B,∠C的度数分别为2x,3x,4x,
∵四边形ABCD内接于圆,
∴∠A+∠C=∠B+∠D=180°,
∵2x+4x=180,∴x=30.
∴∠A=60°,∠B=90°, ∠C =120°,∠D=180°-90°=90°.
课堂小结
一、圆周角定理的推论1
90°的圆周角所对的弦是直径.
二、圆内接多边形的定义
如果一个圆经过一个多边形的各个顶点,这个圆就叫做这个多边形的外接圆,这个多边形叫做这个圆的内接多边形.
三、圆周角定理的推论2
圆内接四边形的对角互补.
课堂训练
1.(2023西藏)如图,四边形ABCD内接于⊙O,E为BC延长线上一点.若∠DCE=65°,则∠BOD的度数是( )
A.65° B.115° C.130° D.140°
C
课堂训练
2.(2023泰安)如图,AB是⊙O的直径,D,C是⊙O上的点,∠ADC=115°,则∠BAC的度数是( )
A.25° B.30° C.35° D.40°
A
课堂训练
3.(2022日照)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为 cm.
课堂训练
4.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
B
课堂训练
5.如图,O为坐标原点,点E的坐标为(0,4),点C在⊙A上,BE是⊙A的一条弦,若tan∠OBE= ,则⊙A的直径的长为 .
第27章 圆
27.1 圆的认识
3.圆周角
第2课时 圆周角定理的推论
华师大版-数学-九年级下册
学习目标
1.能够理解和掌握圆周角定理的推论;
【重点】能运用圆周角定理的推论解决简单的证明或计算.【难点】理解掌握圆周角定理的推论及其证明过程和运用.
2.了解圆周角和直径的关系以及圆内接四边形的概念.
新课导入
如图所示,在这个圆形人工湖边上造4个休息亭(即A,B,C,D),用仪器测得∠A=75°,∠B=65°,能求出另两个角∠C和∠D的度数吗?需要哪些数据可以求该圆形人工湖的直径?
新知探究
问题 上一课时我们证明了半圆或直径所对的圆周角都是90°,那么反过来,如图,圆周角∠BAC=90°,弦BC是直径吗 为什么
解:连结OB,OC,
∵圆周角∠BAC=90°,
∴圆心角∠BOC=180°,即BOC是一条线段,
∴BC是☉O的一条直径.
圆周角定理的推论1 90°的圆周角所对的弦是直径.
知识点 圆周角定理的推论1
1
新知探究
【例1】从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
B
新知探究
【例2】如图所示,已知经过原点的⊙P与x轴、y轴分别交于A,B两点,C是弧AB上一点,则∠ACB的度数是( )
A.80° B.90°
C.100° D.无法确定
B
【解析】连结AB,∵∠AOB=90°,∴AB是⊙P的直径.∴∠ACB=90°.
新知探究
总 结
1.有直径,通常作直径所对的圆周角,从而得出两直线互相垂直,简记为“见直径作直角 ”.
2.有90°的圆周角,通常作直径,简记为“有直角作直径”.
新知探究
1.圆内接多边形
定义:如果一个圆经过一个多边形的各个顶点,这个圆就叫做这个多边形的外接圆,这个多边形叫做这个圆的内接多边形.
圆内接四边形有什么性质呢?
知识点 圆周角定理的推论2
2
新知探究
2.圆周角定理的推论2
问题1 如图,A,B,C,D是☉O上的四点,AC为☉O的直径,请问∠BAD与∠BCD之间有什么关系
解:∵AC为☉O的直径,
∴∠ADC=∠ABC=90°,
∴∠BAD+∠BCD=180°.
新知探究
问题2 在☉O上移动点C,如图,∠BAD与∠BCD之间的关系还成立吗
解:∵优弧BCD和劣弧BAD的度数和为360°
那么它们所对的圆心角的和也是360°,
即∠BAD+∠BCD=180°.
∴它们所对的圆周角∠BAD和∠BCD的和是180°,
圆周角定理的推论2 圆内接四边形的对角互补.
新知探究
【例3】四边形ABCD是⊙O的内接四边形,且∠A=110°,∠B=80°,则∠C= ,∠D= .
70°
100°
新知探究
【例4】如图,四边形ABCD内接于⊙O,点E是CB的延长线上一点,∠EBA=125°,则∠D=( )
A.65° B.120° C.125° D.130°
C
新知探究
【例5】在圆内接四边形ABCD中, ∠A,∠B,∠C的度数之比是2︰3︰4.求这个四边形各角的度数.
解:设∠A,∠B,∠C的度数分别为2x,3x,4x,
∵四边形ABCD内接于圆,
∴∠A+∠C=∠B+∠D=180°,
∵2x+4x=180,∴x=30.
∴∠A=60°,∠B=90°, ∠C =120°,∠D=180°-90°=90°.
课堂小结
一、圆周角定理的推论1
90°的圆周角所对的弦是直径.
二、圆内接多边形的定义
如果一个圆经过一个多边形的各个顶点,这个圆就叫做这个多边形的外接圆,这个多边形叫做这个圆的内接多边形.
三、圆周角定理的推论2
圆内接四边形的对角互补.
课堂训练
1.(2023西藏)如图,四边形ABCD内接于⊙O,E为BC延长线上一点.若∠DCE=65°,则∠BOD的度数是( )
A.65° B.115° C.130° D.140°
C
课堂训练
2.(2023泰安)如图,AB是⊙O的直径,D,C是⊙O上的点,∠ADC=115°,则∠BAC的度数是( )
A.25° B.30° C.35° D.40°
A
课堂训练
3.(2022日照)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB=12cm,BC=5cm,则圆形镜面的半径为 cm.
课堂训练
4.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数是( )
A.55° B.60° C.65° D.70°
B
课堂训练
5.如图,O为坐标原点,点E的坐标为(0,4),点C在⊙A上,BE是⊙A的一条弦,若tan∠OBE= ,则⊙A的直径的长为 .
