八年级上册人教版数学期末综合模拟试卷(一)
文档属性
| 名称 | 八年级上册人教版数学期末综合模拟试卷(一) |  | |
| 格式 | docx | ||
| 文件大小 | 664.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 16:37:26 | ||
图片预览



文档简介
八年级上册人教版数学期末综合模拟试卷(一)
一、单选题(每小题3分,共30分)
1.在代数式,,,,,中,分式有( )
A.2个 B.3个 C.4个 D.5个
2.点关于轴对称的点的坐标为( )
A. B. C. D.
3.关于x的方程无解,则k的值为( )
A. B.3 C. D.无法确定
4.已知,,则代数式的值是( )
A.2 B. C.15 D.
5.如图,△ABC的外角的平分线交的延长线于点,若,则的值是( )
A. B. C. D.
6.如图,是△ABC的中线,是的中线,,则三角形的面积是( )
A.6 B.9 C.12 D.18
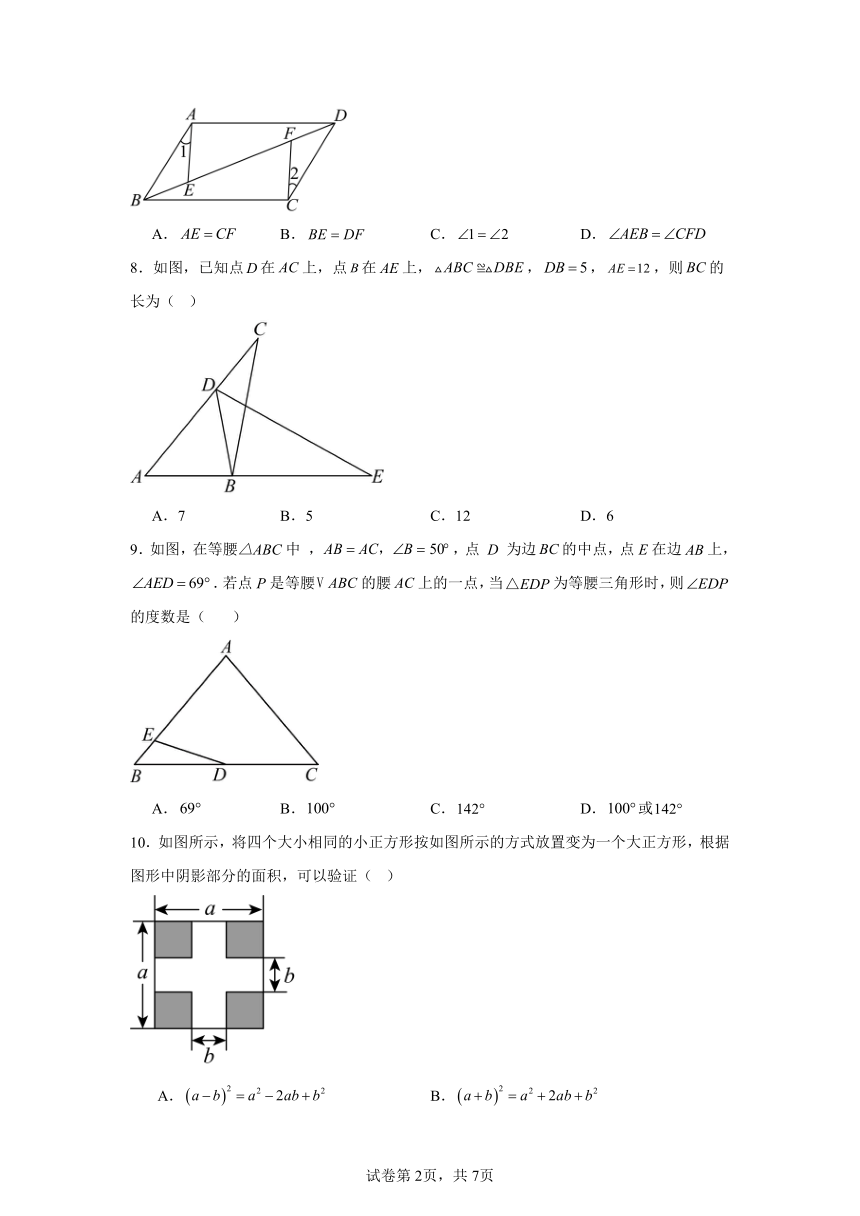
7.如图,在四边形中,,,,是对角线上的两点.若添加一个条件使,则添加的条件不能是( )
A. B. C. D.
8.如图,已知点在上,点在上,,,,则的长为( )
A.7 B.5 C.12 D.6
9.如图,在等腰△ABC中 ,,点 D 为边的中点,点E在边上,.若点P是等腰的腰上的一点,当为等腰三角形时,则的度数是( )
A. B. C. D.或
10.如图所示,将四个大小相同的小正方形按如图所示的方式放置变为一个大正方形,根据图形中阴影部分的面积,可以验证( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
11.若,则 .
12.是一个完全平方式,则m的值是 .
13.若多边形的每个内角都相等,它的一个外角等于,那么这个多边形的内角和等于 °.
14.若的值为,则的值是 .
15.已知,若a,b是等腰三角形的两条边长,则它的周长是 .
16.如图,在△ABC中,点,分别为边,上的点,且,,,则 .
17.如图,数学活动课上,小李同学分别延长和的边,的延长线交于点H,延长线交于点,测得,则 .
18.如图,已知是△ABC的中线,是△BCD的中线,交的延长线于点E.若△ADE的面积为3,则△ABC的面积是 .
三、解答题(共66分)
19.因式分解.(8分)
(1) (2) (3)
20.解分式方程:(8分)
(1) . (2).
21.先化简,再求值:,其中.(6分)
22.先化简后求值: 其中满a足 (6分)
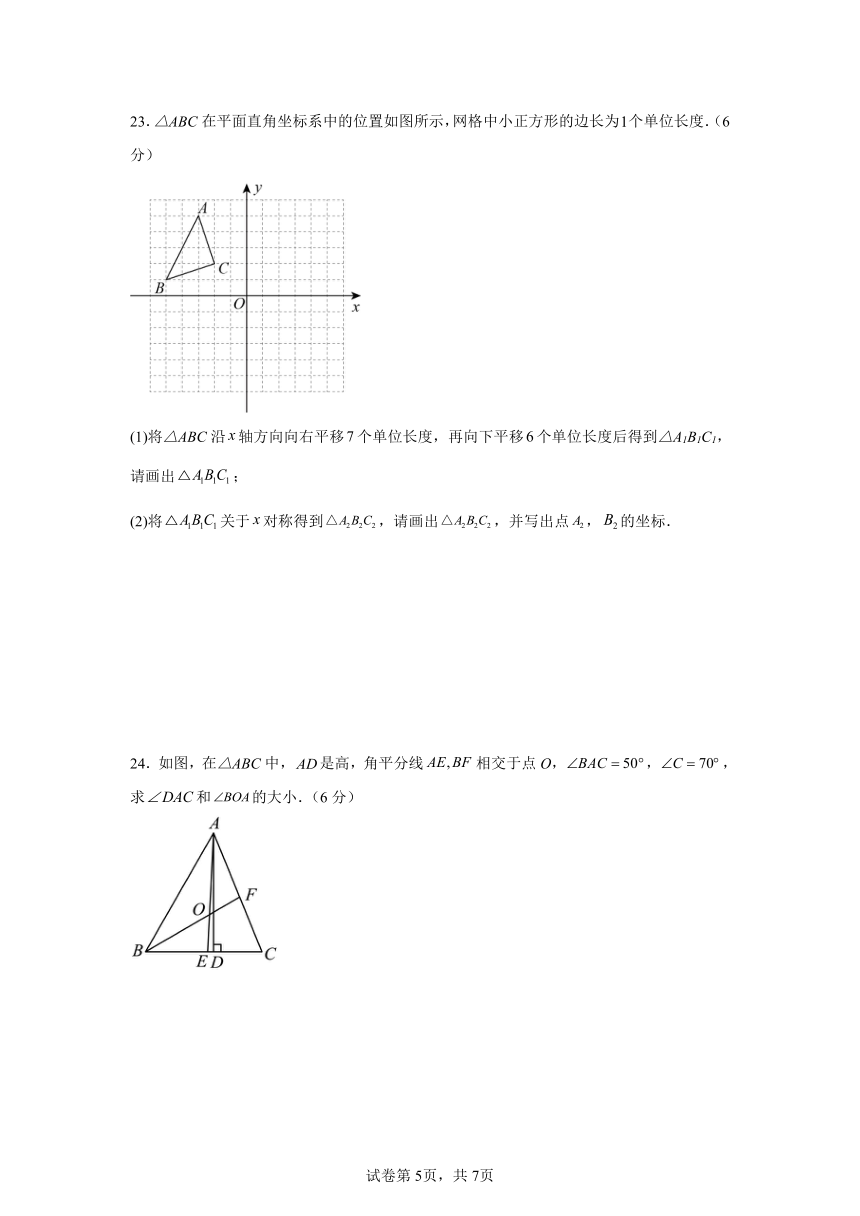
23.△ABC在平面直角坐标系中的位置如图所示,网格中小正方形的边长为个单位长度.(6分)
(1)将△ABC沿轴方向向右平移个单位长度,再向下平移个单位长度后得到△A1B1C1,请画出;
(2)将关于对称得到,请画出,并写出点,的坐标.
24.如图,在△ABC中,是高,角平分线相交于点O,,,求和的大小.(6分)
25.如图,在五边形中,平分,平分,若,求的度数(8分)
26.如图,在外作两个大小不同的等腰直角三角形,其中,,.连接、交于点.(8分)
(1)求证:;
(2)求证:.
27.如图,在四边形中,过点C作于点E,并且,.(10分)
(1)求证:平分;(3分)
(2)若,,求的长;(3分)
(3)若△ABC和△ACD的面积分别为28和16,则△BCE的面积为______.
(4分)试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B D B C A A D A
11.
12.0或6
13.
14.
15.10
16.
17.204
18.12
19.(1)解:(1)
(2)
(3)
20.(1)解:,
,
解得:,
经检验,是原方程的解;
(2)解:
,
解得:,
经检验,是原方程的解.
21.解:
把代入,.
22.解:
,
∵,
∴,
∴原式.
23.(1)解:如图,
∴即为所求;
(2)解:如图,
∴,,即为所求.
24.解:是的高线,
,
在中,
,
;
在中,
,
,
分别平分,相交于点O,
,,
在△AOB中,
.
25.∵
∴
∵多边形是五边形,
∴
∵平分,平分
∴
∴.
26.(1)证明:∵,
∴,
即,
又∵,,
∴;
(2)证明:如图,
∵,
∴,
∵ ,
,
∴,
∴,
∴.
27.(1)证明:如图所示,过点作于点,
∵,
∴,
∵,,
∴,
又∵,
∴,
∴,
∵,
∴是的角平分线,即平分;
(2)解:∵,,
∴,
∵,
∴,
∵平分,
∴,
在△ABC,△ACE中,
,
∴,
∴,
∴;
(3)解:∵,
∴,
∴,
∵,
∴,
∴
∴,
∴.
答案第1页,共2页
答案第1页,共2页
一、单选题(每小题3分,共30分)
1.在代数式,,,,,中,分式有( )
A.2个 B.3个 C.4个 D.5个
2.点关于轴对称的点的坐标为( )
A. B. C. D.
3.关于x的方程无解,则k的值为( )
A. B.3 C. D.无法确定
4.已知,,则代数式的值是( )
A.2 B. C.15 D.
5.如图,△ABC的外角的平分线交的延长线于点,若,则的值是( )
A. B. C. D.
6.如图,是△ABC的中线,是的中线,,则三角形的面积是( )
A.6 B.9 C.12 D.18
7.如图,在四边形中,,,,是对角线上的两点.若添加一个条件使,则添加的条件不能是( )
A. B. C. D.
8.如图,已知点在上,点在上,,,,则的长为( )
A.7 B.5 C.12 D.6
9.如图,在等腰△ABC中 ,,点 D 为边的中点,点E在边上,.若点P是等腰的腰上的一点,当为等腰三角形时,则的度数是( )
A. B. C. D.或
10.如图所示,将四个大小相同的小正方形按如图所示的方式放置变为一个大正方形,根据图形中阴影部分的面积,可以验证( )
A. B.
C. D.
二、填空题(每小题3分,共24分)
11.若,则 .
12.是一个完全平方式,则m的值是 .
13.若多边形的每个内角都相等,它的一个外角等于,那么这个多边形的内角和等于 °.
14.若的值为,则的值是 .
15.已知,若a,b是等腰三角形的两条边长,则它的周长是 .
16.如图,在△ABC中,点,分别为边,上的点,且,,,则 .
17.如图,数学活动课上,小李同学分别延长和的边,的延长线交于点H,延长线交于点,测得,则 .
18.如图,已知是△ABC的中线,是△BCD的中线,交的延长线于点E.若△ADE的面积为3,则△ABC的面积是 .
三、解答题(共66分)
19.因式分解.(8分)
(1) (2) (3)
20.解分式方程:(8分)
(1) . (2).
21.先化简,再求值:,其中.(6分)
22.先化简后求值: 其中满a足 (6分)
23.△ABC在平面直角坐标系中的位置如图所示,网格中小正方形的边长为个单位长度.(6分)
(1)将△ABC沿轴方向向右平移个单位长度,再向下平移个单位长度后得到△A1B1C1,请画出;
(2)将关于对称得到,请画出,并写出点,的坐标.
24.如图,在△ABC中,是高,角平分线相交于点O,,,求和的大小.(6分)
25.如图,在五边形中,平分,平分,若,求的度数(8分)
26.如图,在外作两个大小不同的等腰直角三角形,其中,,.连接、交于点.(8分)
(1)求证:;
(2)求证:.
27.如图,在四边形中,过点C作于点E,并且,.(10分)
(1)求证:平分;(3分)
(2)若,,求的长;(3分)
(3)若△ABC和△ACD的面积分别为28和16,则△BCE的面积为______.
(4分)试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B D B C A A D A
11.
12.0或6
13.
14.
15.10
16.
17.204
18.12
19.(1)解:(1)
(2)
(3)
20.(1)解:,
,
解得:,
经检验,是原方程的解;
(2)解:
,
解得:,
经检验,是原方程的解.
21.解:
把代入,.
22.解:
,
∵,
∴,
∴原式.
23.(1)解:如图,
∴即为所求;
(2)解:如图,
∴,,即为所求.
24.解:是的高线,
,
在中,
,
;
在中,
,
,
分别平分,相交于点O,
,,
在△AOB中,
.
25.∵
∴
∵多边形是五边形,
∴
∵平分,平分
∴
∴.
26.(1)证明:∵,
∴,
即,
又∵,,
∴;
(2)证明:如图,
∵,
∴,
∵ ,
,
∴,
∴,
∴.
27.(1)证明:如图所示,过点作于点,
∵,
∴,
∵,,
∴,
又∵,
∴,
∴,
∵,
∴是的角平分线,即平分;
(2)解:∵,,
∴,
∵,
∴,
∵平分,
∴,
在△ABC,△ACE中,
,
∴,
∴,
∴;
(3)解:∵,
∴,
∴,
∵,
∴,
∴
∴,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
