八年级上册人教版数学期末综合模拟试卷(二)
文档属性
| 名称 | 八年级上册人教版数学期末综合模拟试卷(二) |

|
|
| 格式 | docx | ||
| 文件大小 | 735.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 00:00:00 | ||
图片预览




文档简介
八年级上册人教版数学期末综合模拟试卷(二)
一、单选题(每小题3分,共30分)
1.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2.如果多项式是一个完全平方式,那么的值为( )
A. B. C. D.
3.下列因式分解中正确的个数为( )
①;②;③.
A.个 B.个 C.个 D.个
4.已知点,点与点关于轴对称,则点的坐标是( )
A. B. C. D.
5.下列从左到右的运算是因式分解的是( )
A. B.
C. D.
6.若关于x的分式方程的解为正数,则m的取值范围( )
A. B. C.且 D.且
7.如图,是上一点,交于点,,,若,,则的长是( )
A.2 B.1.5 C.1 D.0.5
8.如图,在中,点E是边的中点,,若,则阴影部分的面积为( )
A.6 B.3 C.4 D.2
9.如图,平分交于点,于点,若,,,则的长为( )
A.2 B.3 C.4 D.5
10.如图,是等边三角形,B、C、D、E四点共线,G、H分别在、上,已知,,则的度数为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.若代数式与的值相等,则= .
12.已知,,则 .
13.若,那么多项式的值是 .
14.在平面直角坐标系中,点关于轴对称的点的坐标为 .
15.在中,,点D在上,于点E,且,连接.若,则的度数为 .
16.如图,中,的平分线交于点E,过点E作于点F.点D在边上,连接、,平分,若,则的面积为 .
17.如图,小明从点出发沿直线前进,到达点后,向左转角度,再沿直线前进,到达点后,又向左转角度,…,照这样走下去,第一次回到出发点,小明共走了,则每次向左转的度数为 .
18.如图,在中,点D为上的一点,,,若,则 .
三、解答题(66分)
19.解分式方程:(8分)
(1) (2)
20.化简下列各式:(8分)
(1); (2).
21.先化简再求值:,其中,.(6分)
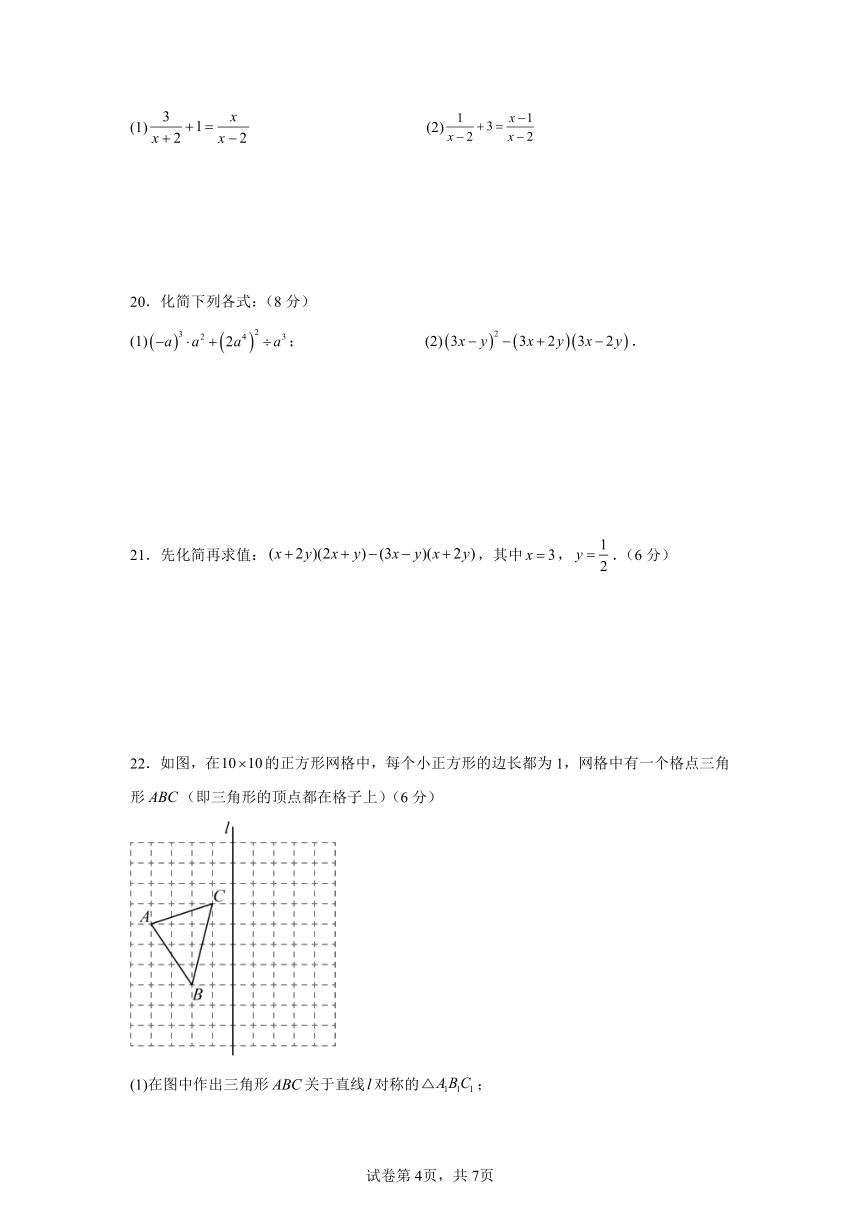
22.如图,在的正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形(即三角形的顶点都在格子上)(6分)
(1)在图中作出三角形关于直线对称的;
(2)求三角形的面积.
23.如图,中,,请用尺规作图法在边上求作一点Q,使得点Q到边的距离等于.(保留作图痕迹,不写作法)(6分)
24.如图,,,是某正多边形相邻的三条边,延长,交于点P,,(6分)
(1)的度数为______;
(2)该多边形为正______边形.
(3)该多边形对角线的总条数是______.
25.如图,在中,点D在边上.(8分)
(1)若,求的度数;
(2)若为的中线,的周长比的周长大3,,求的长.
26.如图①,中,,延长到E,过点E 作交的延长线于点F,延长到G,过点G作交的延长线于点H,且.(8分)
(1)求证:;
(2)如图②连接与相交于点D.若,求的长.
27.综合与探究(10分)
问题情境:在中,,,点D在直线上运动,连接,将线段绕点A顺时针旋转得到线段,过点E作,交直线于点F.
探究发现:
(1)如图1,当点D在上时,与的数量关系是__________.(3分)
(2)如图2,当点D在的延长线上时,连接交于点H.求证:.(3分)
拓展思考:
(3)当,时,直接写出的面积.
(4分)试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D B C A B A D
11.16
12.
13.8
14.
15.35
16.7
17./度
18.
19.(1)解:,
,解得:,
检验:当时,,
∴分式方程的解为:;
(2)解:,
,解得:,
当时,,
∴分式方程无解.
20.(1)解:
.
(2)解:
.
21.解:原式
;
当,时,原式.
22.(1)解:如图,即为所求,
;
(2)解:S△ABC=3×4-1×3× -2×3× -1×4× = .
23.解∶如图,点Q即为所求,
24.(1)解:∵,,是某正多边形相邻的三条边,
∴,
∴,即,
∵,
∴,
故答案为:;
(2)解:∵是正多边形的一个外角,
∴该正多边形的边数为,
故该多边形为正十二边形,
故答案为:十二;
(3)解:∵该多边形为正十二边形,
∴该多边形对角线的总条数是(条),
故答案为:54.
25.(1)解:∵,
∴,
∴,
∴,
∴的度数为;
(2)解:∵为的中线,
∴,
∵的周长比的周长大3,
∴,即,
∴,即,
解得,,
∴的长为6.
26.(1)证明:,,
,
,,
,
在和中,
,
∴,
∴;
(2)解:∵,
,
.
,,
.
在和中,
,
∴,
.
27.解:∵,
∴
又∵
∴
∴
由旋转得,
又∵
∴
∴
在和中,
∴
∴;
(2)由旋转得,
∵
∴
∵
∴
∵
∴,
又在中,
∴,即
在和中,
∴,
∴
又
∴
∵且
∴,
又
∴
在和中,
∴,
∴;
(3)∵,,
∴当点D在的延长线上时,,不满足题意,
∴点D在上,由(1)知,
∴
∴
∵
∴.
当点D在的延长线上时,如图,
同理可得,
∴,
综上,的面积为12或24.
答案第1页,共2页
答案第1页,共2页
一、单选题(每小题3分,共30分)
1.一个多边形的内角和是外角和的2倍,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
2.如果多项式是一个完全平方式,那么的值为( )
A. B. C. D.
3.下列因式分解中正确的个数为( )
①;②;③.
A.个 B.个 C.个 D.个
4.已知点,点与点关于轴对称,则点的坐标是( )
A. B. C. D.
5.下列从左到右的运算是因式分解的是( )
A. B.
C. D.
6.若关于x的分式方程的解为正数,则m的取值范围( )
A. B. C.且 D.且
7.如图,是上一点,交于点,,,若,,则的长是( )
A.2 B.1.5 C.1 D.0.5
8.如图,在中,点E是边的中点,,若,则阴影部分的面积为( )
A.6 B.3 C.4 D.2
9.如图,平分交于点,于点,若,,,则的长为( )
A.2 B.3 C.4 D.5
10.如图,是等边三角形,B、C、D、E四点共线,G、H分别在、上,已知,,则的度数为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.若代数式与的值相等,则= .
12.已知,,则 .
13.若,那么多项式的值是 .
14.在平面直角坐标系中,点关于轴对称的点的坐标为 .
15.在中,,点D在上,于点E,且,连接.若,则的度数为 .
16.如图,中,的平分线交于点E,过点E作于点F.点D在边上,连接、,平分,若,则的面积为 .
17.如图,小明从点出发沿直线前进,到达点后,向左转角度,再沿直线前进,到达点后,又向左转角度,…,照这样走下去,第一次回到出发点,小明共走了,则每次向左转的度数为 .
18.如图,在中,点D为上的一点,,,若,则 .
三、解答题(66分)
19.解分式方程:(8分)
(1) (2)
20.化简下列各式:(8分)
(1); (2).
21.先化简再求值:,其中,.(6分)
22.如图,在的正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形(即三角形的顶点都在格子上)(6分)
(1)在图中作出三角形关于直线对称的;
(2)求三角形的面积.
23.如图,中,,请用尺规作图法在边上求作一点Q,使得点Q到边的距离等于.(保留作图痕迹,不写作法)(6分)
24.如图,,,是某正多边形相邻的三条边,延长,交于点P,,(6分)
(1)的度数为______;
(2)该多边形为正______边形.
(3)该多边形对角线的总条数是______.
25.如图,在中,点D在边上.(8分)
(1)若,求的度数;
(2)若为的中线,的周长比的周长大3,,求的长.
26.如图①,中,,延长到E,过点E 作交的延长线于点F,延长到G,过点G作交的延长线于点H,且.(8分)
(1)求证:;
(2)如图②连接与相交于点D.若,求的长.
27.综合与探究(10分)
问题情境:在中,,,点D在直线上运动,连接,将线段绕点A顺时针旋转得到线段,过点E作,交直线于点F.
探究发现:
(1)如图1,当点D在上时,与的数量关系是__________.(3分)
(2)如图2,当点D在的延长线上时,连接交于点H.求证:.(3分)
拓展思考:
(3)当,时,直接写出的面积.
(4分)试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B D B C A B A D
11.16
12.
13.8
14.
15.35
16.7
17./度
18.
19.(1)解:,
,解得:,
检验:当时,,
∴分式方程的解为:;
(2)解:,
,解得:,
当时,,
∴分式方程无解.
20.(1)解:
.
(2)解:
.
21.解:原式
;
当,时,原式.
22.(1)解:如图,即为所求,
;
(2)解:S△ABC=3×4-1×3× -2×3× -1×4× = .
23.解∶如图,点Q即为所求,
24.(1)解:∵,,是某正多边形相邻的三条边,
∴,
∴,即,
∵,
∴,
故答案为:;
(2)解:∵是正多边形的一个外角,
∴该正多边形的边数为,
故该多边形为正十二边形,
故答案为:十二;
(3)解:∵该多边形为正十二边形,
∴该多边形对角线的总条数是(条),
故答案为:54.
25.(1)解:∵,
∴,
∴,
∴,
∴的度数为;
(2)解:∵为的中线,
∴,
∵的周长比的周长大3,
∴,即,
∴,即,
解得,,
∴的长为6.
26.(1)证明:,,
,
,,
,
在和中,
,
∴,
∴;
(2)解:∵,
,
.
,,
.
在和中,
,
∴,
.
27.解:∵,
∴
又∵
∴
∴
由旋转得,
又∵
∴
∴
在和中,
∴
∴;
(2)由旋转得,
∵
∴
∵
∴
∵
∴,
又在中,
∴,即
在和中,
∴,
∴
又
∴
∵且
∴,
又
∴
在和中,
∴,
∴;
(3)∵,,
∴当点D在的延长线上时,,不满足题意,
∴点D在上,由(1)知,
∴
∴
∵
∴.
当点D在的延长线上时,如图,
同理可得,
∴,
综上,的面积为12或24.
答案第1页,共2页
答案第1页,共2页
同课章节目录
