2.2.1 直线的参数方程 教学设计
文档属性
| 名称 | 2.2.1 直线的参数方程 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 247.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 00:00:00 | ||
图片预览



文档简介
《直线的参数方程》教学设计
【课标要求】
1.掌握直线的参数方程.
2.能够利用直线的参数方程解决有关问题.
【学习目标】
1.会写出直线的参数方程的考查.
2.会利用直线的参数方程中参数t的几何意义求值.
【重难点】
会利用直线的参数方程中参数t的几何意义求值.
【评价任务】
通过例1完成目标1
通过例2完成目标2
教学过程:
一、回忆旧知,做好铺垫
教师提出问题:
1.曲线参数方程的概念及圆与椭圆的参数方程.
2.直线的方向向量的概念.
3.在平面直角坐标系中,确定一条直线的几何条件是什么?
4.已知一条直线的倾斜角和所过的一个定点,请写出直线的方程.
5.如何建立直线的参数方程?
这些问题先由学生思考,回答,教师补充完善,问题5不急于让学生回答,先引起学生的思考.
【设计意图】通过回忆所学知识,为学生推导直线的参数方程做好准备.
二、直线参数方程探究
1.回顾数轴,引出向量
数轴是怎样建立的?数轴上点的坐标的几何意义是什么?
教师提问后,让学生思考并回答问题.
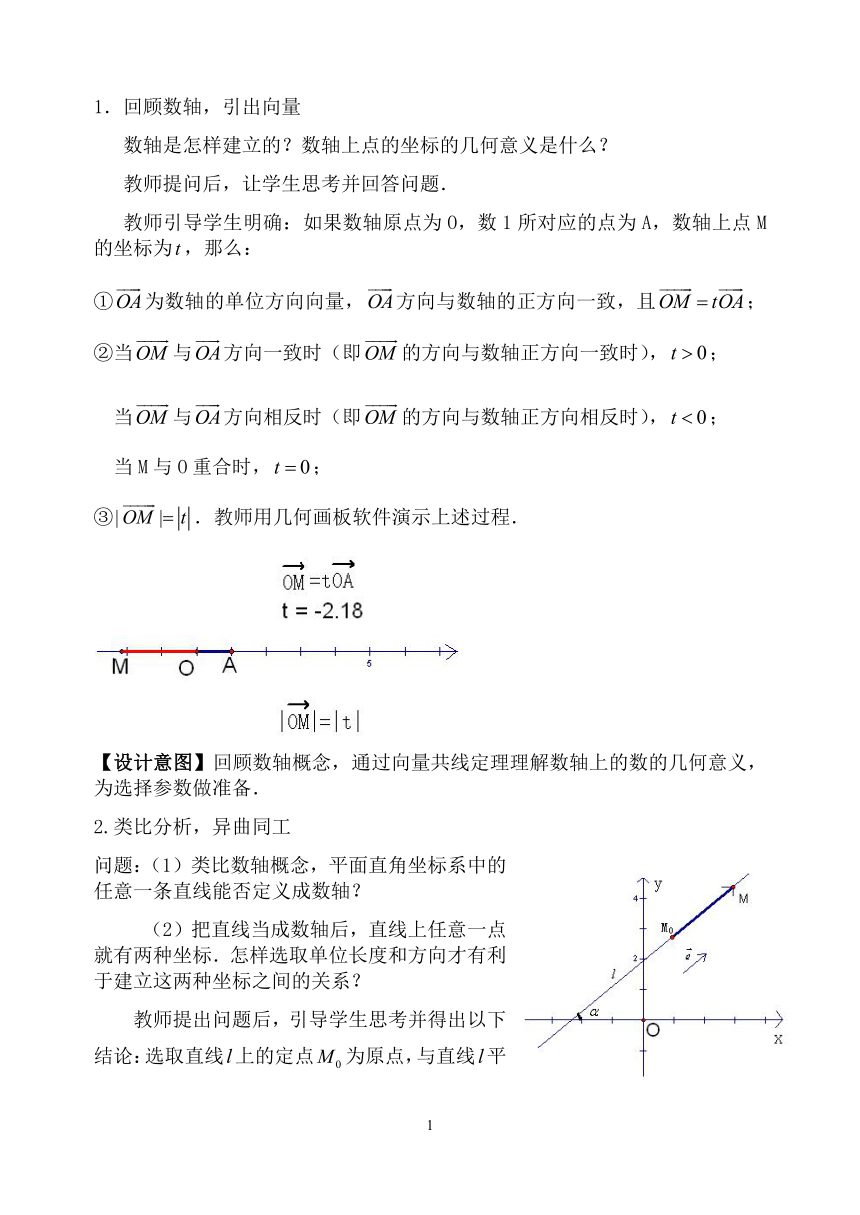
教师引导学生明确:如果数轴原点为O,数1所对应的点为A,数轴上点M的坐标为,那么:
①为数轴的单位方向向量,方向与数轴的正方向一致,且;②当与方向一致时(即的方向与数轴正方向一致时),;
当与方向相反时(即的方向与数轴正方向相反时),;
当M与O重合时,;
③.教师用几何画板软件演示上述过程.
【设计意图】回顾数轴概念,通过向量共线定理理解数轴上的数的几何意义,为选择参数做准备.
2.类比分析,异曲同工
问题:(1)类比数轴概念,平面直角坐标系中的任意一条直线能否定义成数轴?
(2)把直线当成数轴后,直线上任意一点就有两种坐标.怎样选取单位长度和方向才有利于建立这两种坐标之间的关系?
教师提出问题后,引导学生思考并得出以下结论:选取直线上的定点为原点,与直线平行且方向向上(的倾斜角不为0时)或向右(的倾斜角为0时)的单位向量确定直线的正方向,同时在直线上确定进行度量的单位长度,这时直线就变成了数轴.于是,直线上的点就有了两种坐标(一维坐标和二维坐标).在规定数轴的单位长度和方向时,与平面直角坐标系的单位长度和方向保持一致,有利于建立两种坐标之间的联系.
【设计意图】使学生明确平面直角坐标系中的任意直线都可以在规定了原点、单位长度、正方向后成为数轴,为建立直线参数方程作准备.
3. 选好参数,柳暗花明
问题(1):当点M在直线上运动时,点M满足怎样的几何条件?
让学生充分思考后,教师引导学生得出结论:将直线当成数轴后,直线上点M运动就等价于向量变化,但无论向量怎样变化,都有.因此点M在数轴上的坐标决定了点M的位置,从而可以选择作为参数来获取直线的参数方程.
【设计意图】明确参数.
问题(2):如何确定直线的单位方向向量?
教师启发学生:如果所有单位向量起点相同,那么终点的集合就是一个圆.为了研究问题方便,可以把起点放在原点,这样所有单位向量的终点的集合就是一个单位圆.因此在单位圆中来确定直线的单位方向向量.
教师引导学生确定单位方向向量,在此基础上启发学生得出,从而明确直线的方向向量可以由倾斜角来确定.
当时,,所以直线的单位方向向量的方向总是向上.
【设计意图】综合运用所学知识,获取直线的方向向量,培养学生探索精神,体会数形结合思想.
4. 等价转化,深入探究
问题:如果点,M的坐标分别为,怎样用参数表示?
教师启发学生回顾向量的坐标表示,待学生通过独立思考并写出参数方程后再全班交流.过程如下:
因为,(),,
,所以存在实数,使得,即
.
于是,,
即,.
因此,经过定点,倾斜角为的直线的参数方程为
(为参数).
教师提出如下问题让学生加强认识:
①直线的参数方程中哪些是变量?哪些是常量?
②参数的取值范围是什么?
③参数的几何意义是什么?
总结如下:①,是常量,是变量;
②;
③由于,且,得到,因此表示直线上的动点M到定点的距离.当的方向与数轴(直线)正方向相同时,;当的方向与数轴(直线)正方向相反时,;当时,点M与点重合.
【设计意图】把向量转化为坐标,获得了直线的参数方程,在此基础上分析直线参数方程的特点,体会参数的几何意义.
三、运用知识,培养能力
例1.已知直线与抛物线交于A,B两点,求线段AB的长度和点到A,B两点的距离之积.
先由学生思考并动手解决,教师适时点拨、引导,鼓励一题多解,学生可能有以下解法:
解法一:由,得.
设,,由韦达定理得:.
.
由(*)解得,
.
所以.
则
.
解法二、因为直线过定点M,且的倾斜角为,所以它的参数方程是
(为参数), 即 (为参数).
把它代入抛物线的方程,得,
解得,.
由参数的几何意义得:,
.
在学生解决完后,教师投影展示学生的解答过程,予以纠正、完善.然后进行比较:在解决直线上线段长度问题时多了一种解决方法.
【设计意图】通过本题训练,使学生进一步体会直线的参数方程,并能利用参数解决有关线段长度问题,培养学生从不同角度分析问题和解决问题能力以及动手能力.
探究:直线 (为参数)与曲线交于两点,对应的参数分别为.
(1)曲线的弦的长是多少?
(2)线段的中点M对应的参数的值是多少?
先由学生思考,讨论,最后师生共同得到:
,
【设计意图】通过特殊到一般,及时让学生总结有关结论,为进一步应用打下基础,培养归纳、概括能力.
例2、经过点作直线,交椭圆于A,B两点.如果点M恰好为线段AB的中点,求直线的方程.
分析:引导学生以M作为直线上的定点写出直线的参数方程,然后与椭圆的方程联立,设A,B两点对应的参数分别为,则由求出直线的斜率.教师板书,过程如下:
解:设过点的直线的参数方程为(为参数),
代入椭圆方程,整理得
.
因为点M在椭圆内,这个方程必有两个实根,设A,B两点对应的参数分别为,
则.
因为点M为线段AB的中点,所以,即.
于是直线的斜率.
因此,直线的方程是,即.
教师引导学生课下用其他方法解决.
思考:例2的解法对一般圆锥曲线适用吗?把“中点”改为“三等分点”,直线的方程怎样求?由学生课下解决.
【设计意图】体会直线参数方程在解决弦中点问题时的作用.
四、自主解决,深入理解
已知过点,斜率为的直线和抛物线相交于A,B两点,设线段AB的中点为M,求点M的坐标.
本题由学生独立完成,教师补充完善.
解:设过点的直线AB的倾斜角为,由已知可得:,.
所以,直线的参数方程为(为参数).
代入,整理得.
中点M的相应参数是,
所以点M的坐标是.
【设计意图】注重知识的落实,通过问题的解决,使学生进一步理解所学知识.
五、归纳总结,提升认识
先让学生从知识、思想方法以及对本节课的感受等方面进行总结.教师在
学生总结的基础上再进行概括.
1.知识小结
本节课联系数轴、向量等知识,推导出了直线的参数方程,并进行了简单应用,体会了直线参数方程在解决有关问题时的作用.
2.思想方法小结
在研究直线参数方程过程中渗透了运动与变化、类比、数形结合、转化等数学思想.
【设计意图】对学习内容有一个整体的认识,培养归纳、概括能力.
六、布置作业,巩固提高
1. 教材P39—1,3 ;
2. 思考题:若直线的参数方程为 (为常数,为参数),请思考参数的意义.
【设计意图】使学生进一步巩固所学知识,加深对知识的理解,为学有余力的学生提供思考的空间.
七、板书设计
(
直线的参数方程
1.直线的参数方程 3.例题分析
2.弦长公式
)
(
0
)
(
1
)
【课标要求】
1.掌握直线的参数方程.
2.能够利用直线的参数方程解决有关问题.
【学习目标】
1.会写出直线的参数方程的考查.
2.会利用直线的参数方程中参数t的几何意义求值.
【重难点】
会利用直线的参数方程中参数t的几何意义求值.
【评价任务】
通过例1完成目标1
通过例2完成目标2
教学过程:
一、回忆旧知,做好铺垫
教师提出问题:
1.曲线参数方程的概念及圆与椭圆的参数方程.
2.直线的方向向量的概念.
3.在平面直角坐标系中,确定一条直线的几何条件是什么?
4.已知一条直线的倾斜角和所过的一个定点,请写出直线的方程.
5.如何建立直线的参数方程?
这些问题先由学生思考,回答,教师补充完善,问题5不急于让学生回答,先引起学生的思考.
【设计意图】通过回忆所学知识,为学生推导直线的参数方程做好准备.
二、直线参数方程探究
1.回顾数轴,引出向量
数轴是怎样建立的?数轴上点的坐标的几何意义是什么?
教师提问后,让学生思考并回答问题.
教师引导学生明确:如果数轴原点为O,数1所对应的点为A,数轴上点M的坐标为,那么:
①为数轴的单位方向向量,方向与数轴的正方向一致,且;②当与方向一致时(即的方向与数轴正方向一致时),;
当与方向相反时(即的方向与数轴正方向相反时),;
当M与O重合时,;
③.教师用几何画板软件演示上述过程.
【设计意图】回顾数轴概念,通过向量共线定理理解数轴上的数的几何意义,为选择参数做准备.
2.类比分析,异曲同工
问题:(1)类比数轴概念,平面直角坐标系中的任意一条直线能否定义成数轴?
(2)把直线当成数轴后,直线上任意一点就有两种坐标.怎样选取单位长度和方向才有利于建立这两种坐标之间的关系?
教师提出问题后,引导学生思考并得出以下结论:选取直线上的定点为原点,与直线平行且方向向上(的倾斜角不为0时)或向右(的倾斜角为0时)的单位向量确定直线的正方向,同时在直线上确定进行度量的单位长度,这时直线就变成了数轴.于是,直线上的点就有了两种坐标(一维坐标和二维坐标).在规定数轴的单位长度和方向时,与平面直角坐标系的单位长度和方向保持一致,有利于建立两种坐标之间的联系.
【设计意图】使学生明确平面直角坐标系中的任意直线都可以在规定了原点、单位长度、正方向后成为数轴,为建立直线参数方程作准备.
3. 选好参数,柳暗花明
问题(1):当点M在直线上运动时,点M满足怎样的几何条件?
让学生充分思考后,教师引导学生得出结论:将直线当成数轴后,直线上点M运动就等价于向量变化,但无论向量怎样变化,都有.因此点M在数轴上的坐标决定了点M的位置,从而可以选择作为参数来获取直线的参数方程.
【设计意图】明确参数.
问题(2):如何确定直线的单位方向向量?
教师启发学生:如果所有单位向量起点相同,那么终点的集合就是一个圆.为了研究问题方便,可以把起点放在原点,这样所有单位向量的终点的集合就是一个单位圆.因此在单位圆中来确定直线的单位方向向量.
教师引导学生确定单位方向向量,在此基础上启发学生得出,从而明确直线的方向向量可以由倾斜角来确定.
当时,,所以直线的单位方向向量的方向总是向上.
【设计意图】综合运用所学知识,获取直线的方向向量,培养学生探索精神,体会数形结合思想.
4. 等价转化,深入探究
问题:如果点,M的坐标分别为,怎样用参数表示?
教师启发学生回顾向量的坐标表示,待学生通过独立思考并写出参数方程后再全班交流.过程如下:
因为,(),,
,所以存在实数,使得,即
.
于是,,
即,.
因此,经过定点,倾斜角为的直线的参数方程为
(为参数).
教师提出如下问题让学生加强认识:
①直线的参数方程中哪些是变量?哪些是常量?
②参数的取值范围是什么?
③参数的几何意义是什么?
总结如下:①,是常量,是变量;
②;
③由于,且,得到,因此表示直线上的动点M到定点的距离.当的方向与数轴(直线)正方向相同时,;当的方向与数轴(直线)正方向相反时,;当时,点M与点重合.
【设计意图】把向量转化为坐标,获得了直线的参数方程,在此基础上分析直线参数方程的特点,体会参数的几何意义.
三、运用知识,培养能力
例1.已知直线与抛物线交于A,B两点,求线段AB的长度和点到A,B两点的距离之积.
先由学生思考并动手解决,教师适时点拨、引导,鼓励一题多解,学生可能有以下解法:
解法一:由,得.
设,,由韦达定理得:.
.
由(*)解得,
.
所以.
则
.
解法二、因为直线过定点M,且的倾斜角为,所以它的参数方程是
(为参数), 即 (为参数).
把它代入抛物线的方程,得,
解得,.
由参数的几何意义得:,
.
在学生解决完后,教师投影展示学生的解答过程,予以纠正、完善.然后进行比较:在解决直线上线段长度问题时多了一种解决方法.
【设计意图】通过本题训练,使学生进一步体会直线的参数方程,并能利用参数解决有关线段长度问题,培养学生从不同角度分析问题和解决问题能力以及动手能力.
探究:直线 (为参数)与曲线交于两点,对应的参数分别为.
(1)曲线的弦的长是多少?
(2)线段的中点M对应的参数的值是多少?
先由学生思考,讨论,最后师生共同得到:
,
【设计意图】通过特殊到一般,及时让学生总结有关结论,为进一步应用打下基础,培养归纳、概括能力.
例2、经过点作直线,交椭圆于A,B两点.如果点M恰好为线段AB的中点,求直线的方程.
分析:引导学生以M作为直线上的定点写出直线的参数方程,然后与椭圆的方程联立,设A,B两点对应的参数分别为,则由求出直线的斜率.教师板书,过程如下:
解:设过点的直线的参数方程为(为参数),
代入椭圆方程,整理得
.
因为点M在椭圆内,这个方程必有两个实根,设A,B两点对应的参数分别为,
则.
因为点M为线段AB的中点,所以,即.
于是直线的斜率.
因此,直线的方程是,即.
教师引导学生课下用其他方法解决.
思考:例2的解法对一般圆锥曲线适用吗?把“中点”改为“三等分点”,直线的方程怎样求?由学生课下解决.
【设计意图】体会直线参数方程在解决弦中点问题时的作用.
四、自主解决,深入理解
已知过点,斜率为的直线和抛物线相交于A,B两点,设线段AB的中点为M,求点M的坐标.
本题由学生独立完成,教师补充完善.
解:设过点的直线AB的倾斜角为,由已知可得:,.
所以,直线的参数方程为(为参数).
代入,整理得.
中点M的相应参数是,
所以点M的坐标是.
【设计意图】注重知识的落实,通过问题的解决,使学生进一步理解所学知识.
五、归纳总结,提升认识
先让学生从知识、思想方法以及对本节课的感受等方面进行总结.教师在
学生总结的基础上再进行概括.
1.知识小结
本节课联系数轴、向量等知识,推导出了直线的参数方程,并进行了简单应用,体会了直线参数方程在解决有关问题时的作用.
2.思想方法小结
在研究直线参数方程过程中渗透了运动与变化、类比、数形结合、转化等数学思想.
【设计意图】对学习内容有一个整体的认识,培养归纳、概括能力.
六、布置作业,巩固提高
1. 教材P39—1,3 ;
2. 思考题:若直线的参数方程为 (为常数,为参数),请思考参数的意义.
【设计意图】使学生进一步巩固所学知识,加深对知识的理解,为学有余力的学生提供思考的空间.
七、板书设计
(
直线的参数方程
1.直线的参数方程 3.例题分析
2.弦长公式
)
(
0
)
(
1
)
