山东省新泰市2016届九年级下学期学科学习能力成果展示数学试题(含答案)
文档属性
| 名称 | 山东省新泰市2016届九年级下学期学科学习能力成果展示数学试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 258.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-02 00:19:14 | ||
图片预览




文档简介
九年级学科能力水平展示
数 学 试 题
(考试时间150分钟,满分150分)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
一、选择题(本大题共16小题,每小题4分,在每小题给出的四个选项中,只有一个是正确的,请把正确答案序号填涂在答题纸相应的的位置)
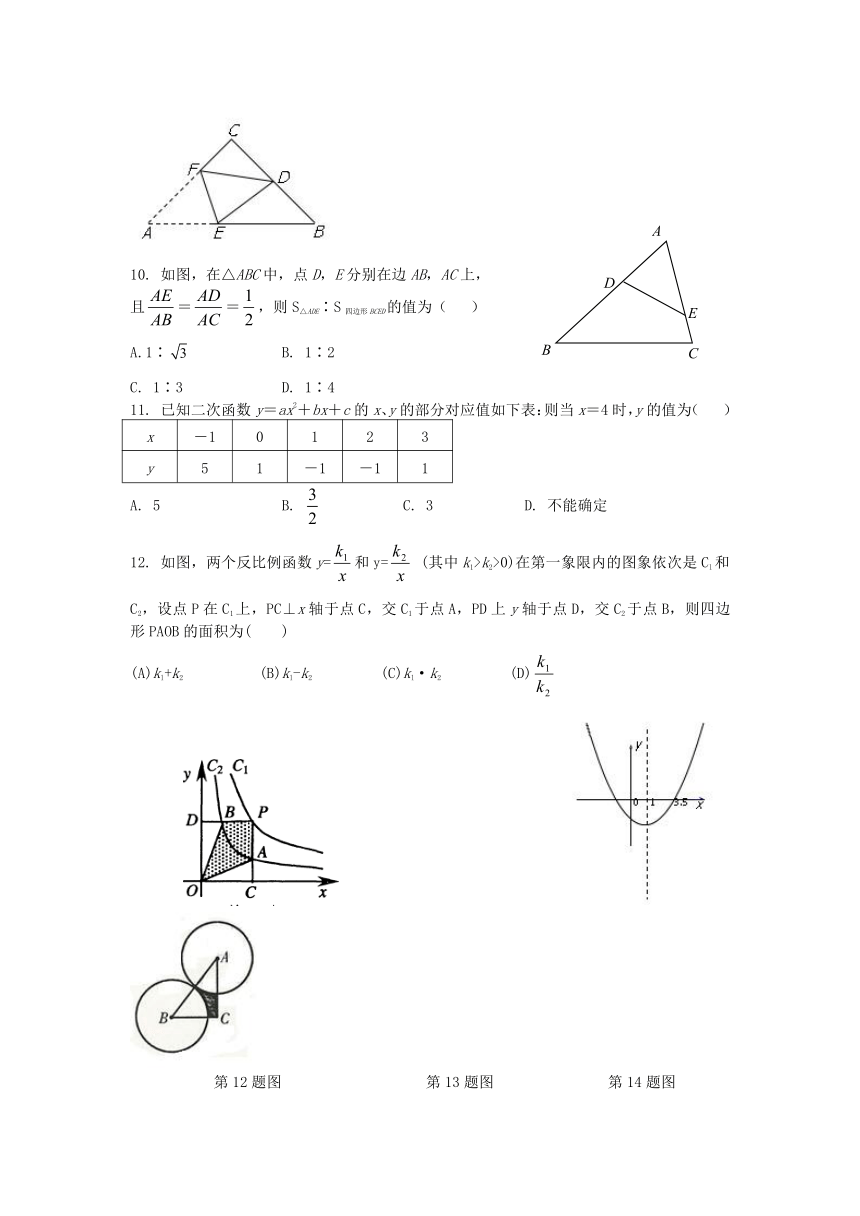
1.若函数y=kx-b的图像如图所示,则关于x的不等式
k(x-3)-b>0的解集为( )
A. x<2 B. x<3 C. x<5 D. x>5
2. 若x为实数,则代数式|x|-x的值一定是( )
A. 正数 B. 非正数 C. 非负数 D. 负数
3. 你认为tan15○的值可能是( )
A. B. C. D.
4. 若,则直线一定通过( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
5. 抛物线y=2x2,y=-2x2,y=x2共有的性质是( )
A. 开口向下 B. 对称轴是y轴 C. 都有最低点 D. y随x的增大而减小
6. 如图,点A,B,C,D的坐标分别是(1,7 ),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A. (6,0) B. (6,3)C. (6,5) D. (4,2) 第6题图
7. 甲、乙两人下棋,甲获胜的概率为30%,和棋的概率为50%,那么乙不输的概率为( )
A.20% B.50% C.70% D.80%
8. 若关于x的方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是
A. k>-1 B. k>-1且k≠0 C. k<1 D. k<1且k≠0
9. 如图,在等腰直角三角形ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使
点A与点D重合,EF为折痕,则sin∠BED的值是( )
A. B. C. D.
10. 如图,在△ABC中,点D,E分别在边AB,AC上,
且==,则S△ADE∶S四边形BCED的值为( )
A.1∶ B. 1∶2
C. 1∶3 D. 1∶4
11. 已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:则当x=4时,y的值为( )
x
-1
0
1
2
3
y
5
1
-1
-1
1
A. 5 B. C. 3 D. 不能确定
12. 如图,两个反比例函数y=和y= (其中k1>k2>0)在第一象限内的图象依次是Cl和C2,设点P在C1上,PC⊥x轴于点C,交C1于点A,PD上y轴于点D,交C2于点B,则四边形PAOB的面积为( )
(A)kl+k2 (B)kl-k2 (C)kl·k2 (D)
第12题图 第13题图 第14题图
13. 如图是二次函数的图象的一部分,对称轴是直线x=1: ① b2>4ac ② 4a-2b+c<0 ③ 不等式ax2+bx+c>0的解集是x>3.5 ④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2上述4个判断中,正确的是( )
A. ①② B. ①④ C. ①③④ D. ②③④
14. 如图在直角△ABC中,∠ACB=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以的长为半径作圆,将直角△ABC截去两个扇形,则剩余(阴影)部分的面积为( )
A. B.
C. D.
15. 如图,A、B、P是半径为2的⊙O上的三点,∠APB =45°,则弦AB的长为( )
A. B. 2 C. D. 4
16.已知一个三角形的三条边长均为正整数.若其中仅有一条边长为5, 第15题图
且它又不是最短边,则满足条件的三角形有( )
A.4 B.6 C.8 D.10
二、填空题(每小题4分,共32分)
17. 一家医院某天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现1个男婴、2个女婴的概率是______.
18. 在等腰直角△ABC中,AB=BC=5,P是△ABC内一点,且PA=,PC=5,则PB=______.
第19题图 第22题图 第23题图
19.如图,已知直线y=x与双曲线y=(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
20. 二次函数的图象与轴正方向交于A,B两点,与轴正方向交于点C.已知,,则 .
21.一辆客车、一辆货车和一辆小轿车在新泰通往泰安的公路上匀速行驶。在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间。过了10分钟,小轿车追上了货车;又过了5分钟小轿车追上了客车;再过t分钟,货车追上了客车。则t=
22.如图,已知四边形ABCD中,AC平分,于点E,且,若,则=______________.
23.如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳。此时,路灯的灯柱BC高度应该设计为 .
24.银座商场经销一种商品,由于进货时价格比原进价降低了6.4%,使得利润率增加了8个百分点,那么经销这种商品原来的利润率是 .
三、解答题(请写出必要的步骤)
25.(本题满分8分)某商家预测一种应季衬衫能畅销市场,就用 13200 元购进了一批这种衬衫,面市后果然供不应求. 商家又用 28800 元购进了第二批这种衬衫,所购数量是第一批购进量的 2 倍,但单价贵了 10 元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下 50 件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于 25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
26.(本题满分8分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
27.(本题满分12分)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
28.(本题满分12分)如图,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为.
⑴求AO与BO的长;
⑵若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图2,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米;
②如图3,当A点下滑到A’点,B点向右滑行到B’点时,梯子AB的中点P也随之运动到P’点.若∠POP’= ,试求AA’的长.
29.(本题满分14分).定义一种变换:平移抛物线得到抛物线,使经过的顶点.设的对称轴分别交于点,点是点关于直线的对称点.
(1)如图1,若:,经过变换后,得到:,点的坐标为,则①的值等于______________;
②四边形为( )
A.平行四边形 B.矩形 C.菱形 D.正方形
(2)如图2,若:,经过变换后,点的坐标为,求的面积;
(3)如图3,若:,经过变换后,,点是直线上的动点,求点到点的距离和到直线的距离之和的最小值.
九年级学科能力水平展示数学试题参考答案
一、选择题:
CBCDB BCBAC A BB AC D
二、填空题:
17、 18、 19、(2,4) 20、 21、15 22、65°
23、米 24、17%
三、解答题:
25、解:(1)设该商家购进的第一批衬衫是件,则第二批衬衫是件
由题意可得:,解得,经检验是原方程的根。
(2)设每件衬衫的标价至少是元
由(1)得第一批的进价为:(元/件),第二批的进价为:(元/件)
由题意可得:
解得,所以,即每件衬衫的标价至少是元。
答:第一批衬衫为120件.每件衬衫的标价至少为150元.
26、(1)证明:∵?ABCD,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.∵∠AFD+∠AFE=180°,∠AFE=∠B,∴∠AFD=∠C在△ADF与△DEC中,
∴△ADF∽△DEC.
(2)解:∵?ABCD,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴,∴DE===12.
在Rt△ADE中,由勾股定理得:
AE===6.
27.解:(1)提示:
在△ADP与△ABQ中
∵
∴△ADP∽△ABQ
(2)作MN⊥QC,则∠QNM=∠QCD=90°,又∵∠MQN=∠PQC
∴△MQN∽△PQC ∴,∵,
又∵
∴
∵ ∴.∵
∴.
在Rt△MBN中,由勾股定理得:
即:
当即时,线段BM长的最小值.
28. (本题满分12分) ⑴中,∠O=,∠α=
∴,∠OAB=,又AB=4米,即∠ACB=∠OAC. ∴米.
米.
⑵设在中,
根据勾股定理:
∴
∴
∵ ∴, ∴ ,
AC=2x=,即梯子顶端A沿NO下滑了米.
⑶∵点P和点分别是的斜边AB与的斜边的中点
∴, ,
∴
∴
∴,∵,∴
∴,∴米.
29.(本题满分14分)解:(1) -2; D;
(2) ∵ : y=a(x-2)2+c-1,而(0,c)在上,可得a=.
∴ DB=(4a+c)-(c-1)=2, ∴ =2.
(3)当点在点的右侧时(如图1),
设AC与BD交于点N,抛物线,配方得,
其顶点坐标是(1,2), ∵ AC=2,∴ 点C的坐标为.
∵过点, ∴解析式为, ∴ B(,
∴ D(,
∴ ,∵ 点与点关于直线对称,
∴,且
∴ 四边形ABCD是菱形. ∴ PD=PB.
作交于点, 则PD+PH=PB+PH.
要使PD+PH最小, 即要使PB+PH最小,
此最小值是点B到AD的距离, 即△ABD边AD上的高.
∵=1,=,,∴=,
故是等边三角形.
∴ ∴ 最小值为.
当点在点的左侧时,同理, 最小值为.
综上,点到点的距离和到直线的距离之和
的最小值为.
数 学 试 题
(考试时间150分钟,满分150分)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
一、选择题(本大题共16小题,每小题4分,在每小题给出的四个选项中,只有一个是正确的,请把正确答案序号填涂在答题纸相应的的位置)
1.若函数y=kx-b的图像如图所示,则关于x的不等式
k(x-3)-b>0的解集为( )
A. x<2 B. x<3 C. x<5 D. x>5
2. 若x为实数,则代数式|x|-x的值一定是( )
A. 正数 B. 非正数 C. 非负数 D. 负数
3. 你认为tan15○的值可能是( )
A. B. C. D.
4. 若,则直线一定通过( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
5. 抛物线y=2x2,y=-2x2,y=x2共有的性质是( )
A. 开口向下 B. 对称轴是y轴 C. 都有最低点 D. y随x的增大而减小
6. 如图,点A,B,C,D的坐标分别是(1,7 ),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
A. (6,0) B. (6,3)C. (6,5) D. (4,2) 第6题图
7. 甲、乙两人下棋,甲获胜的概率为30%,和棋的概率为50%,那么乙不输的概率为( )
A.20% B.50% C.70% D.80%
8. 若关于x的方程kx2-2x-1=0有两个不相等的实数根,则k的取值范围是
A. k>-1 B. k>-1且k≠0 C. k<1 D. k<1且k≠0
9. 如图,在等腰直角三角形ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使
点A与点D重合,EF为折痕,则sin∠BED的值是( )
A. B. C. D.
10. 如图,在△ABC中,点D,E分别在边AB,AC上,
且==,则S△ADE∶S四边形BCED的值为( )
A.1∶ B. 1∶2
C. 1∶3 D. 1∶4
11. 已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:则当x=4时,y的值为( )
x
-1
0
1
2
3
y
5
1
-1
-1
1
A. 5 B. C. 3 D. 不能确定
12. 如图,两个反比例函数y=和y= (其中k1>k2>0)在第一象限内的图象依次是Cl和C2,设点P在C1上,PC⊥x轴于点C,交C1于点A,PD上y轴于点D,交C2于点B,则四边形PAOB的面积为( )
(A)kl+k2 (B)kl-k2 (C)kl·k2 (D)
第12题图 第13题图 第14题图
13. 如图是二次函数的图象的一部分,对称轴是直线x=1: ① b2>4ac ② 4a-2b+c<0 ③ 不等式ax2+bx+c>0的解集是x>3.5 ④若(-2,y1),(5,y2)是抛物线上的两点,则y1<y2上述4个判断中,正确的是( )
A. ①② B. ①④ C. ①③④ D. ②③④
14. 如图在直角△ABC中,∠ACB=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以的长为半径作圆,将直角△ABC截去两个扇形,则剩余(阴影)部分的面积为( )
A. B.
C. D.
15. 如图,A、B、P是半径为2的⊙O上的三点,∠APB =45°,则弦AB的长为( )
A. B. 2 C. D. 4
16.已知一个三角形的三条边长均为正整数.若其中仅有一条边长为5, 第15题图
且它又不是最短边,则满足条件的三角形有( )
A.4 B.6 C.8 D.10
二、填空题(每小题4分,共32分)
17. 一家医院某天出生了3个婴儿,假设生男生女的机会相同,那么这3个婴儿中,出现1个男婴、2个女婴的概率是______.
18. 在等腰直角△ABC中,AB=BC=5,P是△ABC内一点,且PA=,PC=5,则PB=______.
第19题图 第22题图 第23题图
19.如图,已知直线y=x与双曲线y=(k>0)交于A、B两点,点B的坐标为(-4,-2),C为双曲线y=(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
20. 二次函数的图象与轴正方向交于A,B两点,与轴正方向交于点C.已知,,则 .
21.一辆客车、一辆货车和一辆小轿车在新泰通往泰安的公路上匀速行驶。在某一时刻,客车在前,小轿车在后,货车在客车与小轿车的正中间。过了10分钟,小轿车追上了货车;又过了5分钟小轿车追上了客车;再过t分钟,货车追上了客车。则t=
22.如图,已知四边形ABCD中,AC平分,于点E,且,若,则=______________.
23.如图,要在宽为22米的滨湖大道AB两边安装路灯,路灯的灯臂CD长为2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的中轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳。此时,路灯的灯柱BC高度应该设计为 .
24.银座商场经销一种商品,由于进货时价格比原进价降低了6.4%,使得利润率增加了8个百分点,那么经销这种商品原来的利润率是 .
三、解答题(请写出必要的步骤)
25.(本题满分8分)某商家预测一种应季衬衫能畅销市场,就用 13200 元购进了一批这种衬衫,面市后果然供不应求. 商家又用 28800 元购进了第二批这种衬衫,所购数量是第一批购进量的 2 倍,但单价贵了 10 元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下 50 件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于 25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
26.(本题满分8分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
27.(本题满分12分)如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
28.(本题满分12分)如图,一架长4米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为.
⑴求AO与BO的长;
⑵若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.
①如图2,设A点下滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米;
②如图3,当A点下滑到A’点,B点向右滑行到B’点时,梯子AB的中点P也随之运动到P’点.若∠POP’= ,试求AA’的长.
29.(本题满分14分).定义一种变换:平移抛物线得到抛物线,使经过的顶点.设的对称轴分别交于点,点是点关于直线的对称点.
(1)如图1,若:,经过变换后,得到:,点的坐标为,则①的值等于______________;
②四边形为( )
A.平行四边形 B.矩形 C.菱形 D.正方形
(2)如图2,若:,经过变换后,点的坐标为,求的面积;
(3)如图3,若:,经过变换后,,点是直线上的动点,求点到点的距离和到直线的距离之和的最小值.
九年级学科能力水平展示数学试题参考答案
一、选择题:
CBCDB BCBAC A BB AC D
二、填空题:
17、 18、 19、(2,4) 20、 21、15 22、65°
23、米 24、17%
三、解答题:
25、解:(1)设该商家购进的第一批衬衫是件,则第二批衬衫是件
由题意可得:,解得,经检验是原方程的根。
(2)设每件衬衫的标价至少是元
由(1)得第一批的进价为:(元/件),第二批的进价为:(元/件)
由题意可得:
解得,所以,即每件衬衫的标价至少是元。
答:第一批衬衫为120件.每件衬衫的标价至少为150元.
26、(1)证明:∵?ABCD,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.∵∠AFD+∠AFE=180°,∠AFE=∠B,∴∠AFD=∠C在△ADF与△DEC中,
∴△ADF∽△DEC.
(2)解:∵?ABCD,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴,∴DE===12.
在Rt△ADE中,由勾股定理得:
AE===6.
27.解:(1)提示:
在△ADP与△ABQ中
∵
∴△ADP∽△ABQ
(2)作MN⊥QC,则∠QNM=∠QCD=90°,又∵∠MQN=∠PQC
∴△MQN∽△PQC ∴,∵,
又∵
∴
∵ ∴.∵
∴.
在Rt△MBN中,由勾股定理得:
即:
当即时,线段BM长的最小值.
28. (本题满分12分) ⑴中,∠O=,∠α=
∴,∠OAB=,又AB=4米,即∠ACB=∠OAC. ∴米.
米.
⑵设在中,
根据勾股定理:
∴
∴
∵ ∴, ∴ ,
AC=2x=,即梯子顶端A沿NO下滑了米.
⑶∵点P和点分别是的斜边AB与的斜边的中点
∴, ,
∴
∴
∴,∵,∴
∴,∴米.
29.(本题满分14分)解:(1) -2; D;
(2) ∵ : y=a(x-2)2+c-1,而(0,c)在上,可得a=.
∴ DB=(4a+c)-(c-1)=2, ∴ =2.
(3)当点在点的右侧时(如图1),
设AC与BD交于点N,抛物线,配方得,
其顶点坐标是(1,2), ∵ AC=2,∴ 点C的坐标为.
∵过点, ∴解析式为, ∴ B(,
∴ D(,
∴ ,∵ 点与点关于直线对称,
∴,且
∴ 四边形ABCD是菱形. ∴ PD=PB.
作交于点, 则PD+PH=PB+PH.
要使PD+PH最小, 即要使PB+PH最小,
此最小值是点B到AD的距离, 即△ABD边AD上的高.
∵=1,=,,∴=,
故是等边三角形.
∴ ∴ 最小值为.
当点在点的左侧时,同理, 最小值为.
综上,点到点的距离和到直线的距离之和
的最小值为.
同课章节目录
