河南模式2024-2025学年八年级上学期期末数学试卷六(含解析)
文档属性
| 名称 | 河南模式2024-2025学年八年级上学期期末数学试卷六(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-11 21:26:35 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
河南模式2024-2025学年八年级上学期期末数学试卷(六)
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.“一片甲骨惊天下”,甲骨文发源于河南安阳,是我国目前发现最早的文字,其显著特点是图画性强.下列甲骨文图画是轴对称图形的是( )
A. B. C. D.
2.太阳的半径约为696300千米,太阳到地球的距离约为149597870千米,太阳半径与太阳到地球的距离的比值约为0.00465,0.00465用科学记数法可表示为().
A. B. C. D.
3.小李师傅有两根长度分别为和的木条,他想钉一个三角形木框,现有下列长度的几根木条,则他应选择的木条长度是( )
A. B. C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
6.若正多边形的一个内角为,则该正多边形的边数是( )
A.9 B.8 C.7 D.6
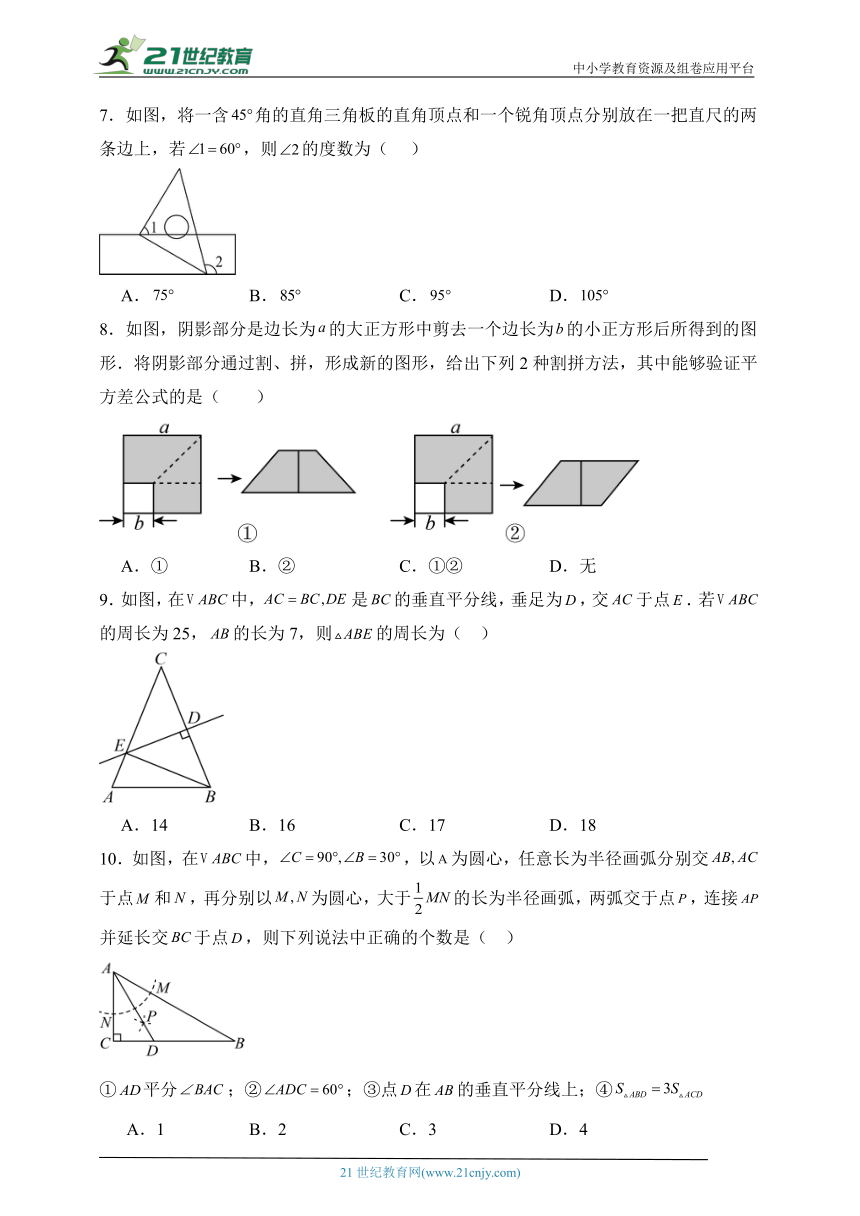
7.如图,将一含角的直角三角板的直角顶点和一个锐角顶点分别放在一把直尺的两条边上,若,则的度数为( )
A. B. C. D.
8.如图,阴影部分是边长为的大正方形中剪去一个边长为的小正方形后所得到的图形.将阴影部分通过割、拼,形成新的图形,给出下列2种割拼方法,其中能够验证平方差公式的是( )
A.① B.② C.①② D.无
9.如图,在中,是的垂直平分线,垂足为,交于点.若的周长为25,的长为7,则的周长为( )
A.14 B.16 C.17 D.18
10.如图,在中,,以为圆心,任意长为半径画弧分别交于点和,再分别以为圆心,大于的长为半径画弧,两弧交于点,连接并延长交于点,则下列说法中正确的个数是( )
①平分;②;③点在的垂直平分线上;④
A.1 B.2 C.3 D.4
第II卷(非选择题)
二、填空题
11.计算: .
12.若分式的值为0,则满足的条件为 .
13.如图所示,分别是锐角和中边的高,且,若要使,可补充的条件是 (只需要填写一个你认为适当的条件即可)
14.如图,在中,,点为上一点,将沿所在直线折叠,点恰好落在边上的点处,且,则的度数为 .
15.如图,中,,点在边上,以为边在右上方作等边,若,则点到边的距离为 .
三、解答题
16.计算:
(1);(2).
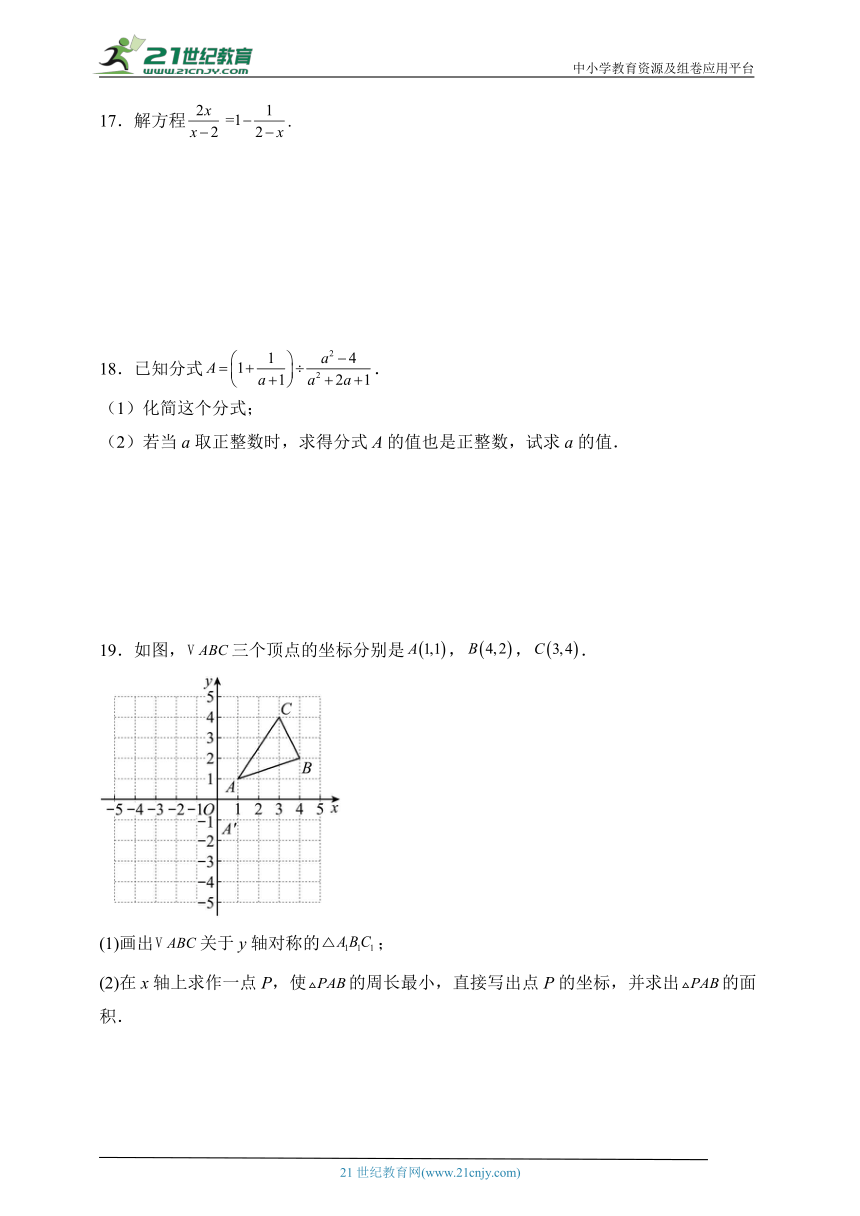
17.解方程.
18.已知分式.
(1)化简这个分式;
(2)若当a取正整数时,求得分式A的值也是正整数,试求a的值.
19.如图,三个顶点的坐标分别是,,.
(1)画出关于y轴对称的;
(2)在x轴上求作一点P,使的周长最小,直接写出点P的坐标,并求出的面积.
20.如图,在中,是上一点,,交于点,.
(1)求证:;
(2)若,,求的长.
21.某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知篮球的单价比足球的单价贵30元,用4500元购买篮球的数量和用3000元购买足球的数量相同、求篮球和足球的单价分别是多少元?
22.如图,在中,,AD是的角平分线,于E,点F在边AC上,连接DF.
(1)求证:;
(2)若,试说明与的数量关系;
(3)在(2)的条件下,若,则BE的长______(用含m,n的代数式表示).
23.教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式;
例如:求代数式的最小值.
原式.
,
当时,有最小值,最小值是.
根据阅读材料用配方法解决下列问题:
(1)分解因式:______;
(2)当为何值时,多项式有最小值,并求出这个最小值;
(3)当______,______时,多项式有最小值,最小值是______.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D A A D C B C
1.B
【分析】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.根据轴对称图形的概念对各选项分析判断即可得解.
【详解】A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:B.
2.C
【分析】用科学记数法的表示方法对数值进行表示即可.
【详解】解:0.00465=4.65×10-3,
故选:C.
【点睛】本题考查了科学记数法,掌握科学记数法的表示方法是解题关键.
3.C
【分析】本题考查的是三角形的三边关系,设木条的长度为,再由三角形的三边关系即可得出结论.
【详解】解:设木条的长度为,则,即.
故选:C.
4.D
【分析】原式各项计算得到结果,即可作出判断.
【详解】A、原式=m4,不符合题意;
B、原式=x2+2x+1,不符合题意;
C、原式=27m6,不符合题意;
D、原式=2a7,符合题意,
故选D.
【点睛】此题考查了整式的混合运算,掌握运算法则是解题的关键.
5.A
【分析】本题主要考查了三角形的稳定性,正确掌握三角形的这一性质是解题的关键.
钉在墙上的方法是构造三角形支架,因而应用了三角形的稳定性.
【详解】这种方法应用的数学知识是:三角形的稳定性,
故选:A.
6.A
【分析】先求出正多边形的每个外角度数,再利用正多边形的外角和求解即可,本题主要考查多边形内角与外角的知识点,解答本题的关键是知道多边形的外角之和为.
【详解】∵正多边形的一个内角是,
∴该正多边形的一个外角为,
∵多边形的外角之和为,
∴边数,
∴该正多边形为正九边形.
故选A.
7.D
【分析】本题考查平行线的性质,三角形的外角,与三角板有关的计算,根据三角板得到的度数,外角得到的度数,平行求出的度数即可.
【详解】解:由题意,得:,,
∴,
∵直尺的对边平行,
∴;
故选D.
8.C
【分析】本题考查平方差公式的几何背景,理解拼图前后各个部分之间的关系,掌握阴影部分面积的计算方法是关键,利用面积法,分别计算左图与右图的阴影部分面积进而可得结论.
【详解】解:图①,左图的阴影部分的面积为,
右图的阴影部分是上底为,下底为,高为的梯形,
因此面积为
所以有,因此图①方法可以验证平方差公式,
图②,左图的阴影部分的面积为,右图的阴影部分是底为,高为的平行四边形,因此面积为,
所以有,因此图②方法也可以验证平方差公式,
故选∶C.
9.B
【分析】
本题主要考查线段的垂直平分线的性质,掌握“线段垂直平分线上的点到这条线段两端点的距离相等”是解题的关键.
先求出,再利用线段的垂直平分线的性质证明,再结合三角形的周长公式计算即可.
【详解】
解:∵的周长为,的长为7, ,
∴,
∵是的垂直平分线,
∴,
∴,
∴的周长.
故选:B
10.C
【分析】先根据三角形内角和计算出,再利用基本作图对①进行判断;利用得到,则可对②进行判断;利用得到,根据线段垂直平分线的性质定理的逆定理可对③进行判断.利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.
【详解】解:由作法得平分,所以①正确;
∵,,
∴,
∴,
∴,所以②正确;
∵,
∴,
∴点D在的垂直平分线上,所以③正确;
∵如图,在直角中,,
∴,
∴,.
∴,
∴,
∴.即,故④错误.
故正确有①②③,共3个,
故选:C.
【点睛】本题考查了作图﹣基本作图.角平分线的性质、线段垂直平分线的性质,直角三角形的性质,等腰三角形的判定与性质,三角形的面积.熟练掌握相关性质定理是解题的关键.
11.4
【分析】针对零指数幂、负整数指数幂分别进行计算,然后根据实数的运算法则计算即可得解.
【详解】解:.
故答案是:
【点睛】本题考查了实数的运算能力,是中考常见题型,解决此类问题的关键是熟练掌握负整数指数幂、零指数幂的考点的运算.
12.
【分析】本题主要考查分式的值为零的条件.根据分式有意义的条件和分式的值为零的条件,列式求解即可.
【详解】解:,,
解得且.
故答案为:.
13.(答案不唯一)
【分析】根据推出,根据全等三角形的性质得出,根据推出全等即可.
【详解】解:,
理由是:
∵分别是锐角和中边的高,
∴,
在和中,
,
∴,
∴,
在和中
,
∴,
故答案为:(答案不唯一).
【点睛】本题考查了全等三角形的判定定理的应用,能熟练地掌握全等三角形的判定定理和性质定理是解此题的关键,注意:全等三角形的判定定理有:,此题是一道开放型的题目,答案不唯一.
14.
【分析】本题考查了折叠的性质,线段垂直平分线的性质,根据题意得出,进一步推出垂直平分是解题关键.
【详解】解:由题意得:
∵,
∴垂直平分
∴
∴
∴
∵
∴
∴的度数为
故答案为:.
15.5
【分析】本题主要考查含角的直角三角形的性质,全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质等知识的综合运用,证明是解题的关键.过E点作于点F,通过证明,得到,进一步得到即可求出结果.
【详解】解:过E点作于点F,
∵,
∴,
∵为等边三角形,
∴,
∴,
∴,
∵在和中
,
∴,
∴,
∵,
∴,
∴,
∴,
即点E到边的距离为.
故答案为:5.
16.(1)
(2)
【分析】(1)根据多项式除以单项式法则计算即可;
(2)先算乘法,再合并同类项.
【详解】(1)解
;
(2)解:
.
【点睛】本题考查的是整式的混合运算,平方差公式,完全平方公式,解题的关键是熟练掌握其运算法则.
17.x=-1.
【分析】首先去掉分母,观察可得最简公分母是(x﹣2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解.
【详解】解:方程两边同乘x-2,得2x=x-2+1
解这个方程,得x= -1
检验:x= -1时,x-2≠0
∴原方程的解是x= -1
18.(1);(2)a=3或a=5
【分析】(1)先算分式的加法,再阿布除法化为乘法,进行约分化简,即可;
(2)把化为,结合当a取正整数时,求得分式A的值也是正整数,即可得到a的值.
【详解】解(1)
=
=
=;
(2)A=
=
=,
∵当a取正整数时,求得分式A的值也是正整数,
∴a-2=1或a-2=3,
∴a=3或a=5.
【点睛】本题主要考查分式的混合运算,掌握分式的通分和约分是解题的关键.
19.(1)画图见解析
(2)画图见解析,,
【分析】(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可得;
(2)作点A关于x轴的对称点,再连接,与x轴的交点即为所求的点P,用长方形等面积减去周围3个小直角三角形的面积即可求出的面积.
【详解】(1)如图所示,即为所求.
(2)如图所示,点即为所求,其坐标为,
.
【点睛】本题主要考查作图 轴对称变换,解题的关键是掌握轴对称变换的定义和性质,并据此得出变换后的对应点.
20.(1)见解析
(2)2
【分析】(1)本题考查平行线性质和全等三角形的判定,根据平行线性质得到,,再结合题干条件即可证明.
(2)本题考查全等三角形性质,根据,得到,再根据即可解题.
【详解】(1)证明:,
,,
在与中,
;
(2)解:,且,,
.
.
21.篮球和足球的单价分别是90元和60元
【分析】本题考查了分式方程的应用,解题的关键是:找准等量关系,正确列出分式方程.
【详解】解:设篮球的单价是元,则足球的单价是元,
由题意,得,
解得,
经检验是原分式方程的解,
答:篮球和足球的单价分别是90元和60元.
22.(1)证明见解析过程;
(2)∠B+∠AFD=180°,理由见解析过程;
(3)
【分析】(1)由于DE⊥AB,那么∠AED=90°,则有∠ACB=∠AED,联合∠CAD=∠BAD,AD=AD,利用AAS即可证明△ACD≌△AED,再根据全等三角形的性质即可得解;
(2)由△ACD≌△AED,证得DC=DE,然后根据HL判定Rt△CDF≌Rt△EDB,得到∠CFD=∠B,再根据邻补角的定义等量代换即可得解;
(3)由AC=AE,CF=BE,根据AB=AE+BE,AC=AF+CF即可得解.
【详解】(1)证明:∵∠C=90°,DE⊥AB,
∴∠C=∠AED=90°,
在△ACD和△AED中,
,
∴△ACD≌△AED(AAS),
∴AC=AE;
(2)解:∠B+∠AFD=180°.
理由如下:
由(1)得:△ACD≌△AED,
∴DC=DE,
在Rt△CDF和Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴∠CFD=∠B.
∵∠CFD+∠AFD=180°,
∴∠B+∠AFD=180°;
(3)解:由(2)知,Rt△CDF≌Rt△EDB,
∴CF=BE,
由(1)知AC=AE.
∵AB=AE+BE,
∴AB=AC+BE.
∵AC=AF+CF,
∴AB=AF+2BE.
∵AB=m,AF=n,
∴.
故答案为:.
【点睛】本题考查了全等三角形的判定和性质,利用AAS证明△ACD≌△AED及利用HL判定Rt△CDF≌Rt△EDB是解此题的关键.
23.(1)
(2)时,最小值为
(3)3,,3
【分析】本题考查配方法的应用,
(1)根据材料用配方法分解因式即可;
(2)根据材料用配方法求出最小值即可;
(3)对多项式利用配方法求出最小值即可.
【详解】(1)解:,
故答案为:;
(2)解:
,
当时,有最小值,最小值是.
(3)解:原式
当时,有最小值,最小值是3.
故答案为:3,,3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
河南模式2024-2025学年八年级上学期期末数学试卷(六)
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.“一片甲骨惊天下”,甲骨文发源于河南安阳,是我国目前发现最早的文字,其显著特点是图画性强.下列甲骨文图画是轴对称图形的是( )
A. B. C. D.
2.太阳的半径约为696300千米,太阳到地球的距离约为149597870千米,太阳半径与太阳到地球的距离的比值约为0.00465,0.00465用科学记数法可表示为().
A. B. C. D.
3.小李师傅有两根长度分别为和的木条,他想钉一个三角形木框,现有下列长度的几根木条,则他应选择的木条长度是( )
A. B. C. D.
4.下列运算正确的是( )
A. B.
C. D.
5.空调安装在墙上时,一般都会采用如图的方法固定,这种方法应用的几何原理是( )
A.三角形的稳定性 B.两点之间线段最短
C.两点确定一条直线 D.垂线段最短
6.若正多边形的一个内角为,则该正多边形的边数是( )
A.9 B.8 C.7 D.6
7.如图,将一含角的直角三角板的直角顶点和一个锐角顶点分别放在一把直尺的两条边上,若,则的度数为( )
A. B. C. D.
8.如图,阴影部分是边长为的大正方形中剪去一个边长为的小正方形后所得到的图形.将阴影部分通过割、拼,形成新的图形,给出下列2种割拼方法,其中能够验证平方差公式的是( )
A.① B.② C.①② D.无
9.如图,在中,是的垂直平分线,垂足为,交于点.若的周长为25,的长为7,则的周长为( )
A.14 B.16 C.17 D.18
10.如图,在中,,以为圆心,任意长为半径画弧分别交于点和,再分别以为圆心,大于的长为半径画弧,两弧交于点,连接并延长交于点,则下列说法中正确的个数是( )
①平分;②;③点在的垂直平分线上;④
A.1 B.2 C.3 D.4
第II卷(非选择题)
二、填空题
11.计算: .
12.若分式的值为0,则满足的条件为 .
13.如图所示,分别是锐角和中边的高,且,若要使,可补充的条件是 (只需要填写一个你认为适当的条件即可)
14.如图,在中,,点为上一点,将沿所在直线折叠,点恰好落在边上的点处,且,则的度数为 .
15.如图,中,,点在边上,以为边在右上方作等边,若,则点到边的距离为 .
三、解答题
16.计算:
(1);(2).
17.解方程.
18.已知分式.
(1)化简这个分式;
(2)若当a取正整数时,求得分式A的值也是正整数,试求a的值.
19.如图,三个顶点的坐标分别是,,.
(1)画出关于y轴对称的;
(2)在x轴上求作一点P,使的周长最小,直接写出点P的坐标,并求出的面积.
20.如图,在中,是上一点,,交于点,.
(1)求证:;
(2)若,,求的长.
21.某中学为落实《教育部办公厅关于进一步加强中小学生体质健康管理工作的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知篮球的单价比足球的单价贵30元,用4500元购买篮球的数量和用3000元购买足球的数量相同、求篮球和足球的单价分别是多少元?
22.如图,在中,,AD是的角平分线,于E,点F在边AC上,连接DF.
(1)求证:;
(2)若,试说明与的数量关系;
(3)在(2)的条件下,若,则BE的长______(用含m,n的代数式表示).
23.教科书中这样写道:“我们把多项式及叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值,最小值等.
例如:分解因式.
原式;
例如:求代数式的最小值.
原式.
,
当时,有最小值,最小值是.
根据阅读材料用配方法解决下列问题:
(1)分解因式:______;
(2)当为何值时,多项式有最小值,并求出这个最小值;
(3)当______,______时,多项式有最小值,最小值是______.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D A A D C B C
1.B
【分析】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.根据轴对称图形的概念对各选项分析判断即可得解.
【详解】A、不是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、不是轴对称图形,故本选项不符合题意.
故选:B.
2.C
【分析】用科学记数法的表示方法对数值进行表示即可.
【详解】解:0.00465=4.65×10-3,
故选:C.
【点睛】本题考查了科学记数法,掌握科学记数法的表示方法是解题关键.
3.C
【分析】本题考查的是三角形的三边关系,设木条的长度为,再由三角形的三边关系即可得出结论.
【详解】解:设木条的长度为,则,即.
故选:C.
4.D
【分析】原式各项计算得到结果,即可作出判断.
【详解】A、原式=m4,不符合题意;
B、原式=x2+2x+1,不符合题意;
C、原式=27m6,不符合题意;
D、原式=2a7,符合题意,
故选D.
【点睛】此题考查了整式的混合运算,掌握运算法则是解题的关键.
5.A
【分析】本题主要考查了三角形的稳定性,正确掌握三角形的这一性质是解题的关键.
钉在墙上的方法是构造三角形支架,因而应用了三角形的稳定性.
【详解】这种方法应用的数学知识是:三角形的稳定性,
故选:A.
6.A
【分析】先求出正多边形的每个外角度数,再利用正多边形的外角和求解即可,本题主要考查多边形内角与外角的知识点,解答本题的关键是知道多边形的外角之和为.
【详解】∵正多边形的一个内角是,
∴该正多边形的一个外角为,
∵多边形的外角之和为,
∴边数,
∴该正多边形为正九边形.
故选A.
7.D
【分析】本题考查平行线的性质,三角形的外角,与三角板有关的计算,根据三角板得到的度数,外角得到的度数,平行求出的度数即可.
【详解】解:由题意,得:,,
∴,
∵直尺的对边平行,
∴;
故选D.
8.C
【分析】本题考查平方差公式的几何背景,理解拼图前后各个部分之间的关系,掌握阴影部分面积的计算方法是关键,利用面积法,分别计算左图与右图的阴影部分面积进而可得结论.
【详解】解:图①,左图的阴影部分的面积为,
右图的阴影部分是上底为,下底为,高为的梯形,
因此面积为
所以有,因此图①方法可以验证平方差公式,
图②,左图的阴影部分的面积为,右图的阴影部分是底为,高为的平行四边形,因此面积为,
所以有,因此图②方法也可以验证平方差公式,
故选∶C.
9.B
【分析】
本题主要考查线段的垂直平分线的性质,掌握“线段垂直平分线上的点到这条线段两端点的距离相等”是解题的关键.
先求出,再利用线段的垂直平分线的性质证明,再结合三角形的周长公式计算即可.
【详解】
解:∵的周长为,的长为7, ,
∴,
∵是的垂直平分线,
∴,
∴,
∴的周长.
故选:B
10.C
【分析】先根据三角形内角和计算出,再利用基本作图对①进行判断;利用得到,则可对②进行判断;利用得到,根据线段垂直平分线的性质定理的逆定理可对③进行判断.利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.
【详解】解:由作法得平分,所以①正确;
∵,,
∴,
∴,
∴,所以②正确;
∵,
∴,
∴点D在的垂直平分线上,所以③正确;
∵如图,在直角中,,
∴,
∴,.
∴,
∴,
∴.即,故④错误.
故正确有①②③,共3个,
故选:C.
【点睛】本题考查了作图﹣基本作图.角平分线的性质、线段垂直平分线的性质,直角三角形的性质,等腰三角形的判定与性质,三角形的面积.熟练掌握相关性质定理是解题的关键.
11.4
【分析】针对零指数幂、负整数指数幂分别进行计算,然后根据实数的运算法则计算即可得解.
【详解】解:.
故答案是:
【点睛】本题考查了实数的运算能力,是中考常见题型,解决此类问题的关键是熟练掌握负整数指数幂、零指数幂的考点的运算.
12.
【分析】本题主要考查分式的值为零的条件.根据分式有意义的条件和分式的值为零的条件,列式求解即可.
【详解】解:,,
解得且.
故答案为:.
13.(答案不唯一)
【分析】根据推出,根据全等三角形的性质得出,根据推出全等即可.
【详解】解:,
理由是:
∵分别是锐角和中边的高,
∴,
在和中,
,
∴,
∴,
在和中
,
∴,
故答案为:(答案不唯一).
【点睛】本题考查了全等三角形的判定定理的应用,能熟练地掌握全等三角形的判定定理和性质定理是解此题的关键,注意:全等三角形的判定定理有:,此题是一道开放型的题目,答案不唯一.
14.
【分析】本题考查了折叠的性质,线段垂直平分线的性质,根据题意得出,进一步推出垂直平分是解题关键.
【详解】解:由题意得:
∵,
∴垂直平分
∴
∴
∴
∵
∴
∴的度数为
故答案为:.
15.5
【分析】本题主要考查含角的直角三角形的性质,全等三角形的判定与性质,等腰三角形的性质,等边三角形的性质等知识的综合运用,证明是解题的关键.过E点作于点F,通过证明,得到,进一步得到即可求出结果.
【详解】解:过E点作于点F,
∵,
∴,
∵为等边三角形,
∴,
∴,
∴,
∵在和中
,
∴,
∴,
∵,
∴,
∴,
∴,
即点E到边的距离为.
故答案为:5.
16.(1)
(2)
【分析】(1)根据多项式除以单项式法则计算即可;
(2)先算乘法,再合并同类项.
【详解】(1)解
;
(2)解:
.
【点睛】本题考查的是整式的混合运算,平方差公式,完全平方公式,解题的关键是熟练掌握其运算法则.
17.x=-1.
【分析】首先去掉分母,观察可得最简公分母是(x﹣2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解.
【详解】解:方程两边同乘x-2,得2x=x-2+1
解这个方程,得x= -1
检验:x= -1时,x-2≠0
∴原方程的解是x= -1
18.(1);(2)a=3或a=5
【分析】(1)先算分式的加法,再阿布除法化为乘法,进行约分化简,即可;
(2)把化为,结合当a取正整数时,求得分式A的值也是正整数,即可得到a的值.
【详解】解(1)
=
=
=;
(2)A=
=
=,
∵当a取正整数时,求得分式A的值也是正整数,
∴a-2=1或a-2=3,
∴a=3或a=5.
【点睛】本题主要考查分式的混合运算,掌握分式的通分和约分是解题的关键.
19.(1)画图见解析
(2)画图见解析,,
【分析】(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可得;
(2)作点A关于x轴的对称点,再连接,与x轴的交点即为所求的点P,用长方形等面积减去周围3个小直角三角形的面积即可求出的面积.
【详解】(1)如图所示,即为所求.
(2)如图所示,点即为所求,其坐标为,
.
【点睛】本题主要考查作图 轴对称变换,解题的关键是掌握轴对称变换的定义和性质,并据此得出变换后的对应点.
20.(1)见解析
(2)2
【分析】(1)本题考查平行线性质和全等三角形的判定,根据平行线性质得到,,再结合题干条件即可证明.
(2)本题考查全等三角形性质,根据,得到,再根据即可解题.
【详解】(1)证明:,
,,
在与中,
;
(2)解:,且,,
.
.
21.篮球和足球的单价分别是90元和60元
【分析】本题考查了分式方程的应用,解题的关键是:找准等量关系,正确列出分式方程.
【详解】解:设篮球的单价是元,则足球的单价是元,
由题意,得,
解得,
经检验是原分式方程的解,
答:篮球和足球的单价分别是90元和60元.
22.(1)证明见解析过程;
(2)∠B+∠AFD=180°,理由见解析过程;
(3)
【分析】(1)由于DE⊥AB,那么∠AED=90°,则有∠ACB=∠AED,联合∠CAD=∠BAD,AD=AD,利用AAS即可证明△ACD≌△AED,再根据全等三角形的性质即可得解;
(2)由△ACD≌△AED,证得DC=DE,然后根据HL判定Rt△CDF≌Rt△EDB,得到∠CFD=∠B,再根据邻补角的定义等量代换即可得解;
(3)由AC=AE,CF=BE,根据AB=AE+BE,AC=AF+CF即可得解.
【详解】(1)证明:∵∠C=90°,DE⊥AB,
∴∠C=∠AED=90°,
在△ACD和△AED中,
,
∴△ACD≌△AED(AAS),
∴AC=AE;
(2)解:∠B+∠AFD=180°.
理由如下:
由(1)得:△ACD≌△AED,
∴DC=DE,
在Rt△CDF和Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴∠CFD=∠B.
∵∠CFD+∠AFD=180°,
∴∠B+∠AFD=180°;
(3)解:由(2)知,Rt△CDF≌Rt△EDB,
∴CF=BE,
由(1)知AC=AE.
∵AB=AE+BE,
∴AB=AC+BE.
∵AC=AF+CF,
∴AB=AF+2BE.
∵AB=m,AF=n,
∴.
故答案为:.
【点睛】本题考查了全等三角形的判定和性质,利用AAS证明△ACD≌△AED及利用HL判定Rt△CDF≌Rt△EDB是解此题的关键.
23.(1)
(2)时,最小值为
(3)3,,3
【分析】本题考查配方法的应用,
(1)根据材料用配方法分解因式即可;
(2)根据材料用配方法求出最小值即可;
(3)对多项式利用配方法求出最小值即可.
【详解】(1)解:,
故答案为:;
(2)解:
,
当时,有最小值,最小值是.
(3)解:原式
当时,有最小值,最小值是3.
故答案为:3,,3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
