专题03 简单机械和功(实验专题训练)(含解析)2024-2025学年九年级物理上学期期末复习专题训练(苏科版)
文档属性
| 名称 | 专题03 简单机械和功(实验专题训练)(含解析)2024-2025学年九年级物理上学期期末复习专题训练(苏科版) |

|
|
| 格式 | docx | ||
| 文件大小 | 779.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-12 00:00:00 | ||
图片预览



文档简介
2024-2025学年九年级物理上学期期末复习专题训练
专题03简单机械和功(实验专题训练)
【计算1杠杆的平衡条件】
1.巴南区某学校在开展物理兴趣小组活动时,学生为深入探究平衡木的平衡,小萍设计了如图所示的装置。轻质杠杆AOB可绕支点O无摩擦转动,且AB=3m,OA=1m。在杠杆A端用不可伸长的细线悬挂正方体M,质量为40kg,边长为20cm。当重为500N的小萍静止站立在OB之间某处时,正方体M对地面压力刚好为0,杠杆同时在水平位置处于平衡状态。求:
(1)正方体M的重力;
(2)当正方体M对地面压力刚好为0时,小萍距O点的距离;
(3)如果小萍站立在距离B端1.5m处时,正方体M对水平地面的压强。
2.杆秤是我国古老且至今仍在使用的一种衡量工具,如图的杆秤可视为杠杆,提纽处为支点O,若不计其自重,当在挂钩悬挂被称物体后处于平衡状态,已知CO=2厘米,OD=20厘米,秤砣的重力为10牛,求:
(1)被称物体的重力;
(2)若这杆秤所能测物体的最大重力为200牛,求OB的长度。
3.如图所示是锅炉保险阀门的示意图。当阀门受到的蒸汽压力超过其安全值时,阀门就会被拉开。其中OB=1m,OA=0.25m,阀门的底面积为2cm2,锅炉内气体压强的安全值为6×105Pa,杠杆的重力、摩擦均不计,锅炉外的大气压p0=1×105Pa。求:
(1)当阀门刚好被拉开时,蒸汽对阀门向上的压力;
(2)当阀门刚好被拉开时,A点受到的压力大小;
(3)B点所挂重物的重力大小。
4.如图所示,一个重为20N、边长为10cm的实心正方体M,悬挂在轻质杠杆B端,OB:OA=5:4,当M的一半体积浸在水中时,在A端施加一个竖直向下的拉力F使杠杆在水平位置平衡。(水的密度为1.0×103kg/m3,g取10N/kg)求:
(1)M底部受到的水对它的压强;
(2)M受到的水对它的浮力;
(3)F的大小。
5.小明发现一个不吸水的新型圆台体建筑材料,测得其重力为12N。他用弹簧测力计和杠杆设计了如图所示的装置进行实验,轻质杠杆OB可绕O点转动,圆台体材料用细绳悬挂在杠杆上A点,容器M中装有水并置于水平地面,当杠杆在水平位置平衡时B端竖直向上的拉力F为0.5N,此时圆台体材料浸没在水中静止且未触底。已知ρ水=1.0×103kg/m3,g取10N/kg,求:
(1)当轻质杠杆在水平位置平衡时,细绳对圆台体材料的拉力;
(2)当轻质杠杆在水平位置平衡时,圆台体材料受到的浮力;
(3)圆台体材料的密度。
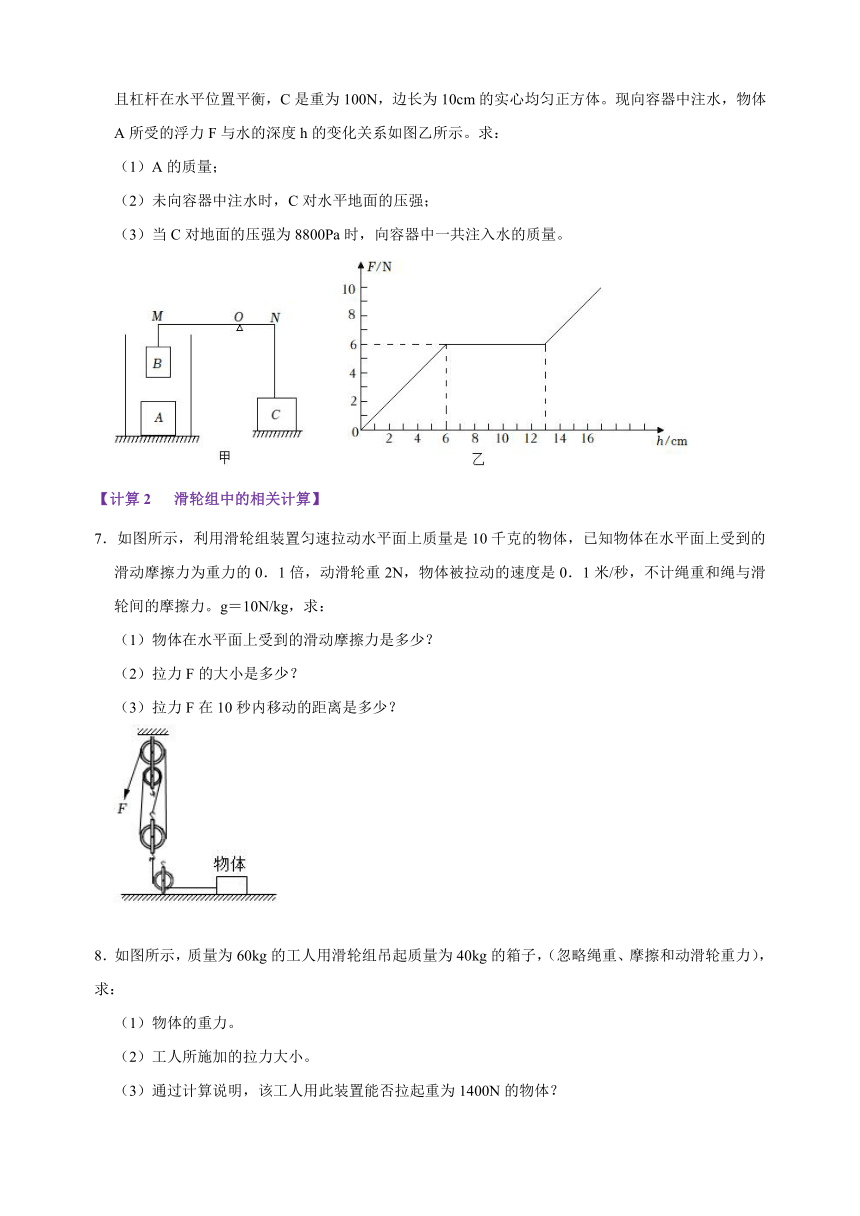
6.如图甲所示,MN是以O为支点的轻质杠杆,OM:ON=4:1,物体A是棱长为10cm的实心均匀正方体,将A自由放置在底面积为200cm2的薄壁柱形容器中,在A的正上方是一个质量为1kg、底面积为60cm2、高为10cm的长方体B,用轻质细杆分别将B和C竖直连接在杠杆M、N两端,且杠杆在水平位置平衡,C是重为100N,边长为10cm的实心均匀正方体。现向容器中注水,物体A所受的浮力F与水的深度h的变化关系如图乙所示。求:
(1)A的质量;
(2)未向容器中注水时,C对水平地面的压强;
(3)当C对地面的压强为8800Pa时,向容器中一共注入水的质量。
【计算2 滑轮组中的相关计算】
7.如图所示,利用滑轮组装置匀速拉动水平面上质量是10千克的物体,已知物体在水平面上受到的滑动摩擦力为重力的0.1倍,动滑轮重2N,物体被拉动的速度是0.1米/秒,不计绳重和绳与滑轮间的摩擦力。g=10N/kg,求:
(1)物体在水平面上受到的滑动摩擦力是多少?
(2)拉力F的大小是多少?
(3)拉力F在10秒内移动的距离是多少?
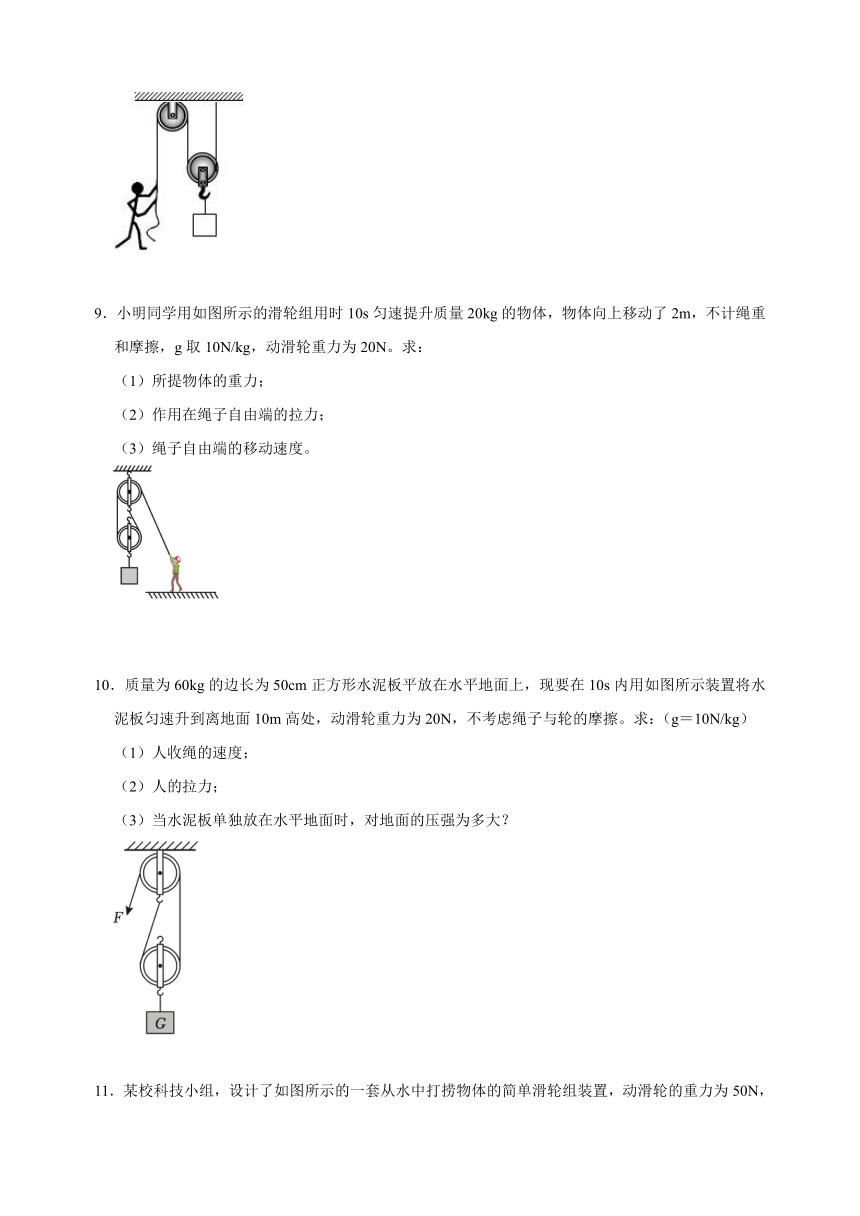
8.如图所示,质量为60kg的工人用滑轮组吊起质量为40kg的箱子,(忽略绳重、摩擦和动滑轮重力),求:
(1)物体的重力。
(2)工人所施加的拉力大小。
(3)通过计算说明,该工人用此装置能否拉起重为1400N的物体?
9.小明同学用如图所示的滑轮组用时10s匀速提升质量20kg的物体,物体向上移动了2m,不计绳重和摩擦,g取10N/kg,动滑轮重力为20N。求:
(1)所提物体的重力;
(2)作用在绳子自由端的拉力;
(3)绳子自由端的移动速度。
10.质量为60kg的边长为50cm正方形水泥板平放在水平地面上,现要在10s内用如图所示装置将水泥板匀速升到离地面10m高处,动滑轮重力为20N,不考虑绳子与轮的摩擦。求:(g=10N/kg)
(1)人收绳的速度;
(2)人的拉力;
(3)当水泥板单独放在水平地面时,对地面的压强为多大?
11.某校科技小组,设计了如图所示的一套从水中打捞物体的简单滑轮组装置,动滑轮的重力为50N,物体A的质量为60kg,体积为0.04m3;通过滑轮组把A从水中匀速提升,不计绳重、摩擦及水的阻力,ρ水=1×103kg/m3。求:
(1)A浸没在水中所受浮力;
(2)A露出水面前,绳子自由端的拉力;
(3)若人的重力为625N,与水平地面的接触面积为500cm2,物体A出水后,求人对地面的压强。
【计算3 功的计算和公式的应用】
12.“绿水青山就是金山银山”,为了保护环境,我国大力发展电动汽车替代传统燃油汽车。表中是某种电动汽车的部分参数,假设车上只有司机一人,质量为60kg,汽车在水平公路匀速行驶时所受阻力为总重力的0.04倍,电动汽车充满电后以最高速度匀速行驶60km。(g=10N/kg)求:
空车质量 1340kg
轮胎与地面总接触面积 320cm2
电池容量 42kW h
最高速度 120km/h
(1)行驶这段路程所用的时间;
(2)电动汽车在水平公路匀速行驶时牵引力的大小;
(3)电动汽车匀速行驶60km,牵引力所做的功。
13.如图是小伟同学在单杠上做引体向上时的情景,每次引体向上身体上升的高度为0.6m,求解下列问题。(小伟的质量为50kg,g取10N/kg)
(1)引体向上前小伟先进行了热身训练,他绕操场跑了600m用时5min,求他热身运动的平均速度。
(2)小伟的体重是多少?
(3)小伟完成1次引体向上克服重力做的功。
(4)小伟做完引体向上运动后,双脚稳稳地站在水平地面上,请你计算他此时对地面的压强。(小伟每个鞋底的底面积为250cm2)
14.一质量为5t的载重货车,现装有质量为25t的货物以20m/s的速度匀速行驶在水平公路上,已知货车共有4个车轮,每个车轮与地面接触面积为1.5dm2,汽车匀速行驶时,受到的阻力是总重的0.1倍,求:
(1)货车停下后对地面的压强;
(2)货车匀速行驶10s牵引力做的功。
15.重为5N的空鱼缸,放在水平窗台上,其底面与窗台的接触面积为0.01m2,如图,向鱼缸内注入1.5kg的水,水的深度为10cm。假设小明沿竖直方向把盛水的鱼缸匀速抬高0.3m。(g取10N/kg,水的密度为1.0×103kg/m3)求:
(1)空鱼缸对窗台的压强;
(2)注水后鱼缸底部受到水的压强;
(3)抬高鱼缸的过程中,小明对鱼缸和水总共做的功。
16.“背漂”是儿童游泳时常佩戴的一种救生装置。某款长方体“背漂”重为1.5N,底面积为375cm2。把足够大的柱形容器放在水平台面上,用不可伸长的细线一端与“背漂”的底面相连,另一端固定在容器底部,如图甲。往容器中缓慢持续注水,注水过程中细线的拉力F与水的深度h的关系如图乙所示,求:
(1)注水过程中,“背漂”受到的最大浮力;
(2)细线的长度;
(3)注水过程中,浮力对“背漂”所做的功。
17.如图甲所示,质量为3kg的物块,在拉力F的作用下在水平面上做直线运动。拉力随时间变化、速度随时间变化图象分别如图乙、丙所示,已知物块在0~6s的运动距离为6m。求(g取10N/kg):
(1)物块的重力;
(2)在2~4s内物块运动的平均速度;
(3)在前6s内,拉力F做的功。
【计算4 功率的计算及公式的应用】
18.某科研所新研发了一款微型机器人,它可拖动比自身重大很多的物体。机器人质量是1.2×10﹣2kg,它静止在水平地面上时,与地面的接触面积是1×10﹣4m2。求:
(1)它受到的重力是多少?
(2)静止时,它对水平地面的压强是多少?
(3)若它用110N的水平拉力在10s内匀速拖动重物前进1m,则拉力的功率是多少?
19.2021年6月25日,西藏自治区首条电气化铁路拉林铁路开通运营,历史性地实现复兴号动车组对31个省区市的全覆盖,翻开了西藏和高原铁路建设发展新篇章。旦增乘坐某次列车从拉萨去林芝旅游,列车经过平直的藏木特大桥时,如图甲所示,他用手表测量了自己通过大桥的时间,上桥和离桥时的手表示数如图乙所示。通过查询资料得知列车功率约为5×106W,若列车过桥时速度保持25m/s不变。求:
(1)旦增过桥所用的时间;
(2)大桥的长度;
(3)列车过桥时所受阻力的大小。
20.一质量为5t的载重货车,现装有质量为25t的货物以20m/s的速度匀速行驶在水平公路上,汽车匀速行驶时,受到的阻力是总重的0.1倍(g取10N/kg),求:
(1)货车匀速行驶1h,牵引力做的功;
(2)若整个过程中货车的功率不变,货车上坡时的牵引力需增大为水平路面的2倍,求车上坡时的速度。
21.为助力乡村振兴,中山市某街道将生态农业和旅游观光相结合,打造美丽乡村。如图是该街道夏日乡村游用的观光艇,其部分技术参数如表:(g=10N/kg,ρ水=1.0×103kg/m3)
商品名称 浪花牌观光艇
商品型号 长7.5m×宽2.0m×深0.9m
空船质量 800kg
发动机最大输出功率 40kW
最大载人数量 8人
最大航速 10m/s
(1)若人的质量为50kg,当观光艇满载时,所受的浮力是多少?
(2)当观光艇以最大速度匀速航行时,受到水的平均阻力为多大?航行2km,发动机做功多少?
(3)小曾观察到艇身上标注的最大吃水线为50cm。当吃水达到该位置时,水对艇底部的压强是多大?
22.“海斗号”自主遥控水下机器人由中国科学院沈阳自动化研究所研发,最大潜深达10767米。海斗号成为我国首台下潜深度超过万米并进行科考应用的无人自主潜水器,海斗号总质量为35t,体积为60m3。(此前国内下潜深度最大的载人潜水器为蛟龙号,ρ海水≈1×103kg/m3,g=10N/kg)
(1)海斗号在我国首次万米深渊科考航次中,累计下潜七次,其中五次下潜是深度大于8000米的深渊科考应用,求第一次下潜到8000米时海斗号所受海水压强的大小。
(2)海斗号下潜到8000米后打开探照灯,摄像头通过观测孔了解8000米处深海的秘密,假设观测孔的面积为4dm2,求此时观测孔所受海水压力的大小。
(3)海斗号在完成某次任务后,匀速直线上升返回海面。若海斗号在水中以0.5m/s的速度匀速上浮,求浮力做功的功率和海斗号所受海水阻力大小。(设海斗号所受海水阻力大小不变)
23.如图所示,动滑轮重4N,所吊重物B重20N,物体A重240N,此时物体B恰好在20s内匀速下降了2m,不计绳重、绳子的伸长和滑轮组内部的摩擦。求:
(1)物体B下降的速度是多大?
(2)水平面对物体A的摩擦力是多大?
(3)要使物体B恰好以0.2m/s的速度匀速上升,则要对物体A施加水平向右拉力F的功率为多大?
【计算5 机械效率的计算】
24.图甲是某落锤式打桩机实物图,打桩机是利用冲击力将桩打入地层的桩工机械。其原理示意图如图乙所示。桩锤由卷扬机用吊钩提升,释放后自由下落而打桩。已知桩锤的质量为400kg,桩锤的底面积为0.1m2,桩顶的面积为0.04m2。求(g取10N/kg):
(1)若桩锤下落打在桩上的压力为4×105N,此时桩锤对桩的压强。
(2)若卷扬机把桩锤匀速提升2m,所用时间为2s,在此提升过程中打桩机的功率为8×103W。
①此过程中的有用功。
②此过程中打桩机的机械效率。
25.今年以来云南干旱少雨,为解决生活用水,扎西同学用一台功率为500W的抽水机将水从井中抽往12m高的楼顶水箱中,用时10min把容积为2m3的水箱装满。求:
(1)水箱中水的质量;
(2)抽水机抽水过程中对水做的有用功;
(3)抽水机抽水时的效率。
26.图1所示为工人师傅乘坐吊篮在高空粉刷楼体外墙的情景,吊篮可在电动机的作用下实现升降,其简化结构原理如图2所示。吊篮的质量为60kg,两名工人及工具的总质量为240kg,某次吊升过程中,吊篮在30s内匀速上升了6m。不计滑轮重、绳重和摩擦。
(1)电动机对绳子的拉力?
(2)电动机对吊篮(包括人及工具)做的功和功率?
(3)对吊篮做的功为额外功,对人和工具做的功为有用功,则机械效率是多少?
27.某型号挖掘机的实物图(甲)和作业范围图(乙)以及部分相关数据表,如图所示。挖掘机在4s内将装满铲斗的泥土从最大挖掘深度处送到位于最大卸料高度的装载车上。
项目 数值
满斗泥土的质量(kg) 600
A最大挖掘深度(m) 3
B最大卸料高度(m) 5
(1)移送泥土过程中,挖掘机对泥土做的功。
(2)移送泥土过程中,挖掘机的总功率为20kW,此过程中挖掘机的效率。
(3)挖掘机所做的额外功可将500N的物体抬高几米。
【计算6 滑轮(组)的机械效率】
28.如图所示,分别直接用力F1和使用滑轮用力F2,拉着高为h、底面积为S、质量为m的同一长方体金属块在同一水平路面上做匀速直线运动,移动L的距离。求:
(1)图中金属块静放在地面时对地面的压强;
(2)拉力在使用滑轮的过程中做的总功;
(3)该滑轮的机械效率。
29.如图所示,物体重180N,动滑轮重20N,绳重和轴摩擦不计。在竖直向上的拉力F的作用下,物体上升了4m。
(1)求绳子自由端移动的距离;
(2)求此过程中所做的额外功;
(3)求此过程中所做的有用功;
(4)求机械效率。
30.小南利用图甲的滑轮组,将一实心长方体以0.2m/s的速度匀速从水底拉出水面,图乙是该实心长方体所受拉力F1随时间t变化的图像。(不计摩擦、水的阻力及绳重)。求:
(1)实心长方体浸没时受到的浮力;
(2)实心长方体从水底到露出水面前,上升的高度;
(3)实心长方体从水底到露出水面前,若人对绳的拉力F2做功400J,求此过程中滑轮组的机械效率。
31.如图所示,工人借助滑轮组把重为350N的货物匀速提升了3m,已知绳子端拉力大小为200N,忽略摩擦及绳重。求:
(1)绳子自由端移动的距离和动滑轮的重。
(2)工人做的有用功。
(3)工人做的额外功。
(4)滑轮组的的机械效率。
32.如图甲所示,质量为40kg的小荣同学站在高台上竖直向上匀速拉动绳子,脚与地面的总接触面积为0.04m2,现改变G物,计算并绘出机械效率η与G物的关系图像如图乙所示,不计绳重和摩擦,求:
(1)动滑轮的重力G动;
(2)当G物=120N时,若此时人在10s内将物体提升了2m,则此时拉力的功率;
(3)若人站的位置能承受的最大压强为12500Pa,则该滑轮组所能提升物体的最大机械效率。
33.如图所示,某考古队用滑轮组将体积为100dm3的文物打捞出水,定滑轮重100N。滑轮组上共有三根绳子a、b和c,其中a是悬挂定滑轮,b绕在定滑轮和动滑轮上,c悬挂文物,整个打捞过程始终缓慢匀速提升文物,匀速提升文物0.5m(文物一直完全浸没在水中)时滑轮组所做的有用功为1.9×103J,滑轮组的机械效率为95%(g=10N/kg,绳重、滑轮与轴的摩擦以及水的阻力均忽略不计)。请解答下列问题:
(1)文物浸没在水中时受到的浮力是多大?
(2)动滑轮的重力是多大?
(3)在整个打捞过程中,a、b、c三根绳中哪根绳承受的拉力最大?该绳至少要承受多大的拉力?
【计算7 杠杆的机械效率】
34.用如图所示的杠杆从水平位置开始提升重物,用F=30N的动力始终竖直向上,将重为G=60N的物体缓慢提升0.1m,已知OA:OB=1:3,OA:OC=1:4,支点处的摩擦不计,求:
(1)杠杆自重G杆。
(2)杠杆提升重物的机械效率η。
(3)若将动力作用点从B点移到C点,其它条件不变,请说明杠杆的机械效率怎么变化?
35.如图所示,用竖直向上的拉力F作用在杠杆末端A点,将挂在杠杆中点B的重为150N的物体匀速缓慢提升0.5m。A点沿竖直方向上升1m。已知杠杆的质量分布均匀,自重为30N。(不计绳重及摩擦)
(1)求力F的大小;
(2)求将重物匀速提升时杠杆的机械效率(结果保留到0.1%)。
36.如图所示是一种小型千斤顶示意图,当手往下压动摇臂时,能把重物抬高一段较小的距离,工人在10s时间内用100N的力竖直向下压动摇臂2m,把1000N的重物匀速抬高14cm。
试求:
(1)工人做的功;
(2)此千斤顶的机械效率。
【计算8 斜面的机械效率】
37.如图,一辆货车匀速从山底A开到山顶B。货车重为5.0×104N,货车发动机的功率保持不变,山坡AB长2000m,高h为300m,牵引力保持2.5×104N不变,不计空气阻力。求:
(1)汽车从山底开到山顶所做的有用功。
(2)山坡的机械效率。
(3)汽车在山坡上行驶时的摩擦力。
38.如图所示,斜面长5m,高3m,物体A的重力为200N,物体B的重力280N,动滑轮的重力为20N。滑轮组绳子平行于斜面连接物体A,在滑轮组与物体B的作用下,能使物体A由斜面底端被匀速拉至顶端(不计绳重、滑轮与绳间的摩擦力、空气阻力)。
求:(1)绳子拉力F对物体A所做的有用功多少?
(2)该斜面的机械效率多少?
(3)物体A受到的滑动摩擦力多少?
39.如图所示,斜面长5m,小明用绳子沿与水平面成30度角的斜面将重为300N的木块由斜面底端匀速拉到顶端,拉力大小为240N,绳重不计。求:
(1)斜面对木块的摩擦力多大。
(2)斜面的机械效率。
40.如图所示,利用斜面将箱子推进车厢,通常要比把箱子直接从地面搬进车厢省力多了,某同学用150N的力沿斜面向上匀速推动箱子,已知箱子质量为30kg,斜面长3m,斜面高1.2m,g=10N/kg。求:
(1)箱子受到的重力;
(2)箱子受到的摩擦力;
(3)斜面的机械效率;
(4)使用斜面推箱子时有哪些更省力的方法。
参考答案
【计算1杠杆的平衡条件】
1.见试题解答内容
【分析】(1)知道正方体M的质量,根据G=mg求出正方体M的重力;
(2)根据杠杆平衡条件求出小萍离O点的距离;
(3)小萍站立在距离B端1.5m处时,根据杠杆的平衡条件求出A端细线的拉力,正方体M对水平地面的压力等于自身的重力减少绳子的拉力,受力面积等于正方体M的底面积,利用p=求出正方体M对水平地面的压强。
【解答】解:(1)由G=mg可得,正方体M的重力:
G木=m木g=40kg×10N/kg=400N;
(2)M对地面的压力刚好为0,则地面对M的支持力也为0,对M做受力分析,它受到竖直向下的重力和竖直向上的拉力,且拉力与重力相等,即F拉=G木=400N,
杠杆对重物M的拉力F拉与重物M对杠杆的拉力F1相等,即F1=F拉=400N;
设小萍离O点的距离为l2,由杠杆平衡条件F1l1=F2l2得F1 OA=G人l2,即:
l2==0.8m;
(3)小萍站立在距离B端L1=1.5m处时,由杠杆的平衡条件可得:
FA OA=G人 (AB﹣OA﹣L1),
即:FA×1m=500N×(3m﹣1m﹣1.5m),
解得:FA=250N,
正方体M对水平地面的压力:
F=GM﹣FA=400N﹣250N=150N,
正方体M对水平地面的压强:p==3.75×103Pa。
答:(1)正方体M的重力400N;
(2)当正方体M对地面压力刚好为0时,小萍距O点的距离0.8m;
(3)如果小萍站立在距离B端1.5m处时,正方体M对水平地面的压强为3.75×103Pa。
2.(1)被称物体的重力为100N;
(2)OB的长度是40cm。
【分析】杆秤是利用杠杆原理工作的,应用杠杆平衡条件分析解答。
(1)已知阻力与阻力臂、动力臂,由杠杆平衡条件可以求出动力,即物体的重力。
(2)已知阻力、阻力臂、动力,由杠杆平衡条件可以求出动力臂。
【解答】解:(1)由杠杆平衡条件得:G物体CO=G秤砣OD,
即:G物体×2cm=10N×20cm,
解得:G物体=100N;
(2)由杠杆平衡条件得:G最大CO=G秤砣OB,
即:200N×2cm=10N×OB,
解得:OB=40cm;
答:(1)被称物体的重力为100N;
(2)OB的长度是40cm。
3.(1)当阀门刚好被拉开时,蒸汽对阀门向上的压力为120N;
(2)当阀门刚好被拉开时,A点受到的压力大小为100N;
(3)B点所挂重物的重力大小为25N。
【分析】(1)根据已知条件,由压强公式得出蒸汽对阀门向上的压力;
(2)由已知条件,根据压强公式得出当阀门刚好被拉开时A点受到的压力大小;
(3)O为支点,当阀门刚好被拉开时,A点受到的压力大小为FA,根据杠杆的平衡条件得出B点所挂重物的重力。
【解答】解:(1)阀门的底面积为2cm2,锅炉内气体压强的安全值为6×105Pa,当阀门受到的蒸汽压力超过其安全值时,阀门就会被拉开,故当阀门刚好被拉开时,根据压强公式,蒸汽对阀门向上的压力
F=pS=6×105Pa×2×10﹣4m2=120N;
(2)锅炉外的大气压p0=1×105Pa,当阀门刚好被拉开时,A点受到的压力大小;
FA=ΔpS=(6×105Pa﹣1×105Pa)×2×10﹣4m2=100N;
(3)O为支点,当阀门刚好被拉开时,A点受到的压力大小为FA,
根据杠杆的平衡条件可知有FA OA=G OB
即100N 0.25m=G 1m
故B点所挂重物的重力:
G=25N。
答:(1)当阀门刚好被拉开时,蒸汽对阀门向上的压力为120N;
(2)当阀门刚好被拉开时,A点受到的压力大小为100N;
(3)B点所挂重物的重力大小为25N。
4.(1)M底部受到的水对它的压强为500Pa;
(2)M受到的水对它的浮力为5N;
(3)F的大小为18.75N。
【分析】(1)当M的一半体积浸在水中时,求出M的底部所处的深度,利用压强公式求M底部受到的水对它的压强;
(2)当M的一半体积浸在液体中时,根据排开水的体积,利用F浮=ρ液V排g求出M受到的水对它的浮力;
(3)根据受力平衡求出M对B点的拉力,利用杠杆平衡条件计算拉力F。
【解答】解:(1)当M的一半体积浸在水中时,M的底部所处的深度:h=L=×10cm=5cm=0.05m,
M底部受到的水对它的压强:p=ρ水gh=1.0×103kg/m3×10N/kg×0.05m=500Pa;
(2)当M的一半体积浸在液体中时,排开水的体积:V排=L3=×(10cm)3=500cm3=5×10﹣4m3,
则此时M受到的水对它的浮力:F浮=ρ水V排g=1.0×103kg/m3×10N/kg×5×10﹣4m3=5N;
(3)M对B点的拉力:FB=G﹣F浮=20N﹣5N=15N,
由杠杆平衡条件可得:FB×OB=F×OA,
则:F===18.75N。
答:(1)M底部受到的水对它的压强为500Pa;
(2)M受到的水对它的浮力为5N;
(3)F的大小为18.75N。
5.(1)当轻质杠杆在水平位置平衡时,细绳对圆台体材料的拉力为2N;
(2)当轻质杠杆在水平位置平衡时,圆台体材料受到的浮力为10N;
(3)圆台体材料的密度为1.2×103kg/m3。
【分析】(1)设绳子对圆台体建筑材料的拉力为F2,则绳子对杠杆的拉力F1=F2,根据杠杆平衡条件可求出绳子对杠杆的拉力F1;
(2)圆台体建筑材料静止在水中,处于平衡状态,根据G=F浮十F2可求出材料浸没在水中静止时受到的浮力;
(3)根据阿基米德原理可求出圆台体的体积,从而求出其密度。
【解答】解:(1)设绳子对圆台体建筑材料的拉力为F2,
绳子对杠杆的拉力F1=F2,
根据杠杆的平衡条件可知:Fl1=F1l2,
即:0.5N×0.4m=F1×0.1m,得出F1=2N,
则细绳对圆台体材料的拉力F2=F1=2N;
(2)圆台体建筑材料静止在水中,处于平衡状态,则:
G=F浮十F2,
材料浸没在水中静止时受到的浮力为:
F浮=G﹣F2=12N﹣2N=10N;
(3)由F浮=G排=ρ水gV排可知,物体的体积为:
V=V排===10﹣3m3,
材料的密度为:ρ材料====1.2×103kg/m3。
答:(1)当轻质杠杆在水平位置平衡时,细绳对圆台体材料的拉力为2N;
(2)当轻质杠杆在水平位置平衡时,圆台体材料受到的浮力为10N;
(3)圆台体材料的密度为1.2×103kg/m3。
6.(1)A的质量为0.6kg;
(2)C对水平地面的压强为6000Pa;
(3)液体的质量为3.1kg。
【分析】(1)由图乙中图表可知,注入水后所受的浮力先增加,然后不变,最后再增大,说明图形中水平的位置就是物体漂浮的过程,由图表可知A受到的浮力,再利用浮沉条件此时F浮=GA可求出A的重力,再用m=可得出A的质量;
(2)由杠杆平衡条件可计算出C所受的拉力,再根据受力分析可以求出所受到的支持力,由于支持力和压力是一对相互作用力,可以求出C对地面的压力,再利用p=可以求出C对地面的压强;
(3)题目已知C的地面的压强,用F=pS可以计算出C对地面的压力,从而得出C所受到的压力,再根据受力分析,可得出C所受的拉力大小,利用杠杆平衡的条件和受力分析,可得出B此时所受到的浮力。
【解答】解:(1)由图象知,当h水深为6﹣13cm时,浮力不变,且小于A的边长,说明没有浸没,故此时物体A漂浮,
再利用浮沉条件此时F浮=GA,所以GA=6N;
所以物体A的重力为6N;
A的质量为m===0.6kg;
(2)当未注入水时,物体B所受到的重力GB=mg=1kg×10N/kg=10N,
利用杠杆平衡条件可知,GBOM=F拉CON,
由于OM:ON=4:1,所以此时C所受到的拉力F拉C=40N,
C所受到支持力F支=GC﹣F拉C=100N﹣40N=60N,
由于压力和支持力互为相互作用力,F压=F支=60N,
由p=可得,C对地面的压强为p===6000Pa;
C对水平地面的压强为6000Pa;
(3)由F=ps可得,此时C对水平地面的压力为F=pS=8800Pa×100cm2=88N;
由于压力和支持力互为相互作用力,C所受到支持力F支′=F压′=88N,
C所受到拉力F拉C′=GC﹣F支′=100N﹣88N=12N,
利用杠杆平衡条件可知,F拉BOM=F拉C′ON,
由于OM:ON=4:1,所以此时B所受到的拉力F拉B=3N,
假设此时A未浸没,
B所受到A的作用力为FA对B=GB﹣F拉B=10N﹣3N=7N,
此时A所受到的浮力为F浮A=GA+FB对A=6N+7N=13N,
而A全浸没所受到的浮力F浮全=ρ液gV排=1×103kg/m3×1000×10﹣6m3×10N/kg=10N,
与假设的条件不符,所以A应该已经全浸没,
那么A所受到B对A的作用力FB对A=F浮全﹣GA=10N﹣6N=4N,
B所受到A对B的作用力FA对B=4N,
B受到的浮力为F浮B=GB﹣FA对B﹣F拉B=10N﹣4N﹣3N=3N,
由F浮=ρ水V排g可得浮体排开水的体积:
V排B=3×10﹣4m3=300cm3,
B浸入深度为:h浸B==5cm,
由图表可知A漂浮且AB之间接触而无作用力的水深为13cm,
由F浮=ρ水V排g可得A排开水的体积:
V排A=6×10﹣4m3=600cm3,
h浸A==6cm,
所以此时水面的深度为:
h水=h浸B+(LA﹣h浸A)+13cm=5cm+(10cm﹣6cm)+13cm=22cm,
那么此时加入的V液=V总﹣V排A﹣V排B=22cm×200cm2﹣1000cm3﹣300 cm3=3100cm3,
液体的质量m液=ρ液V液=1×103kg/m3×3300×10﹣6m3=3.1kg;
答:(1)A的质量为0.6kg;
(2)C对水平地面的压强为6000Pa;
(3)液体的质量为3.1kg。
【计算2 滑轮组中的相关计算】
7.(1)物体在水平面上受到的滑动摩擦力是10N;
(2)拉力F的大小是4N;
(3)拉力F在10秒内移动的距离是3m。
【分析】(1)根据G=mg得出物体的重力,根据f=0.1G得出物体在水平面上受到的滑动摩擦力;
(2)物体匀速运动,处于平衡状态,根据F物=f得出滑轮组对物体的拉力,
从图中可知n=3,不计绳重和绳与滑轮间的摩擦力,根据F=(G动+F物)得出拉力F;
(3)根据s=vt得出物体在10s内移动的距离s,根据s′=ns得出拉力F在10秒内移动的距离。
【解答】解:(1)物体的重力G=mg=10kg×10N/kg=100N,
物体在水平面上受到的滑动摩擦力f=0.1G=0.1×100N=10N;
(2)物体匀速运动,处于平衡状态,滑轮组对物体的拉力F物=f=10N,
从图中可知n=3,不计绳重和绳与滑轮间的摩擦力,拉力F=(G动+F物)=×(2N+10N)=4N;
(3)物体在10s内移动的距离s=vt=0.1m/s×10s=1m,
拉力F在10秒内移动的距离s′=ns=3×1m=3m。
答:(1)物体在水平面上受到的滑动摩擦力是10N;
(2)拉力F的大小是4N;
(3)拉力F在10秒内移动的距离是3m。
8.(1)物体的重力为400N;
(2)工人所施加的拉力大小为200N;
(3)该工人用此装置不能拉起重为1400N的物体。
【分析】(1)根据G=mg求出物体的重力;
(2)根据滑轮组装置确定绳子股数,忽略绳重、摩擦和动滑轮重力,利用F=G求出工人所施加的拉力大小;
(3)根据G=mg求出人的重力,绳子自由端受到最大拉力为人的重力,即F'=G人,利用F'=G'求出工人能拉起的最大物重。
【解答】解:(1)箱子的质量为40kg,故箱子的重力为G=mg=40kg×10N/kg=400N;
(2)由图可知,n=2,忽略绳重、摩擦和动滑轮重力,工人所施加的拉力大小为:
F=G=×400N=200N;
(3)工人的质量为60kg,故工人的重力为G人=m人g=60kg×10N/kg=600N,绳子自由端受到最大拉力为人的重力,即F'=G人=600N,
根据F'=G'可知,工人能拉起的最大物重为:
G'=nF'=2×600N=1200N<1400N,
故该工人用此装置不能拉起重为1400N的物体。
答:(1)物体的重力为400N;
(2)工人所施加的拉力大小为200N;
(3)该工人用此装置不能拉起重为1400N的物体。
9.(1)所提物体的重力为200N;
(2)作用在绳子自由端的拉力为110N;
(3)绳子自由端的移动速度为0.4m/s。
【分析】(1)知道物体的质量,根据G=mg计算出重力;
(2)由图可知n=2,不计绳重和摩擦,根据F=算出绳子自由端的拉力;
(3)根据s=nh算出绳子自由端移动的距离,再利用v=计算出绳子自由端的移动速度。
【解答】解:(1)质量为20kg的物体的重力为
G=mg=20kg×10N/kg=200N;
(2)不计绳重和摩擦,如图,滑轮组的动滑轮和重物由2条绳子共同对它们施加了向上的拉力,因为定滑轮不省力只能改变力的方向,所以绳子自由端的拉力即为重物和动滑轮总重力的一半:
F===110N;
(3)因为n=2,所以绳子自由端移动的距离是物体上升高度的2倍,物体向上移动了2m,所以绳子自由端移动的距离是4m,则绳子自由端的移动速度为
v===0.4m/s。
答:(1)所提物体的重力为200N;
(2)作用在绳子自由端的拉力为110N;
(3)绳子自由端的移动速度为0.4m/s。
10.(1)人收绳的速度为2m/s;
(2)人的拉力为310N;
(3)压强为2400Pa。
【分析】(1)利用速度计算公式求得物体上升的速度,再利用v=nv物求得人收绳的速度;
(2)根据G=mg计算重力,根据图中知,绳子的股数n=2,不计绳重及滑轮摩擦,根据公式F=(G+G动)求出拉力;
(2)根据F=G计算压力,根据p=计算压强。
【解答】解:(1)由题意可得,动滑轮上有两股绳,物体上升的速度为=1m/s,
则人收绳子的速度为v=2v物=2×1m/s=2m/s;
(2)由重力计算公式可得G物=mg=60kg×10N/kg=600N,
不考虑绳子与轮的摩擦,人的拉力为F=(G+G动)=×(600N+20N)=310N;
(3)由题意可得,水泥板放地面时的受力面积为S=50×10﹣2m×50×10﹣2m=0.25m2,
由压强公式可得p==2400Pa。
答:(1)人收绳的速度为2m/s;
(2)人的拉力为310N;
(3)压强为2400Pa。
11.(1)A浸没在水中所受浮力为400N;
(2)A露出水面前,绳子自由端的拉力为125N;
(3)人对地面的压强为6×103Pa。
【分析】(1)根据F浮=ρ液gV排求出A浸没在水中所受浮力;
(2)根据G=mg求出A的重力,根据力的平衡条件求出A浸没在水中时受到的拉力,
由图可知n=2,利用不计绳重和摩擦时F=(F拉+G动)求出绳子自由端的拉力;
(3)物体A出水后,根据F′=(G+G动)求出人对绳子自由端的拉力,此时人对水平地面的压力等于人的重力减去绳子自由端的拉力,根据p=求人对地面的压强。
【解答】解:(1)因为A浸没在水中,所以A排开水的体积:
V排=V=0.04m3,
则A所受的浮力:
F浮=ρ水gV排=1×103kg/m3×10N/kg×0.04m3=400N;
(2)A的重力:
G=mg=60kg×10N/kg=600N,
由力的平衡条件可知,A浸没在水中时受到的拉力:
F拉=G﹣F浮=600N﹣400N=200N,
由图可知n=2,因为不计绳重和摩擦及水的阻力,所以A露出水面前,绳子自由端的拉力:
F=(F拉+G动)=×(200N+50N)=125N;
(3)物体A出水后,人对绳子自由端的拉力:
F′=(G+G动)=×(600N+50N)=325N,
人对水平地面的压力:
F压=G人﹣F′=625N﹣325N=300N,
人对地面的压强:
p===6×103Pa。
答:(1)A浸没在水中所受浮力为400N;
(2)A露出水面前,绳子自由端的拉力为125N;
(3)人对地面的压强为6×103Pa。
【计算3 功的计算和公式的应用】
12.(1)行驶这段路程所用的时间为0.5h;
(2)电动汽车在水平公路匀速行驶时牵引力为560N;
(3)电动汽车匀速行驶60km,牵引力所做的功为3.36×107J。
【分析】(1)已知电动车行驶的路程和速度,根据v=计算行驶这段路程所用的时间;
(2)电动汽车对地面的压力等于汽车和人的总重力,根据G=mg求出总重力;然后求出阻力;由于汽车匀速行驶,汽车受到的牵引力、阻力是一对平衡力,大小相等,据此求出牵引力;
(3)根据W=Fs便可计算出牵引力做的功。
【解答】解:(1)由v=可得,行驶这段路程所用的时间:
t==0.5h;
(2)电动汽车匀速行驶时的总重力为:
G=(m1+m2)g=(1340kg+60kg)×10N/kg=1.4×104N;
电动汽车匀速行驶,所以牵引力与阻力平衡,
则电动汽车受到的牵引力为:
F=f=0.04G=0.04×1.4×104N=560N;
(3)则电动车行驶60km,牵引力做的功为:
W=Fs=560N×60×103m=3.36×107J;
答:(1)行驶这段路程所用的时间为0.5h;
(2)电动汽车在水平公路匀速行驶时牵引力为560N;
(3)电动汽车匀速行驶60km,牵引力所做的功为3.36×107J。
13.(1)小伟热身运动的平均速度为2m/s;
(2)小伟的体重是500N;
(3)小伟完成1次引体向上克服重力做的功为300J;
(4)小伟双脚站在水平地面上时对地面的压强约为1×104Pa。
【分析】(1)知道小伟跑的路程和时间,根据v=求出其平均速度;
(2)利用G=mg计算小伟的体重;
(3)利用W=Gh求出完成1次引体向上做的功;
(4)小伟双脚站在水平地面上对地面的压力等于其重力,根据p=求出他对地面的压强。
【解答】解:(1)小伟热身运动的平均速度为:
v===2m/s;
(2)小伟的体重为:
G=mg=50kg×10N/kg=500N,
(3)完成1次引体向上做的功为:
W=Gh=500N×0.6m=300J;
(4)小伟双脚站在水平地面上对地面的压力为:
F=G=500N,
双脚与地面的接触面积约为:
S=2×250cm2=500cm2=500×10﹣4m2,
则对地面的压强:
p===1×104Pa。
答:(1)小伟热身运动的平均速度为2m/s;
(2)小伟的体重是500N;
(3)小伟完成1次引体向上克服重力做的功为300J;
(4)小伟双脚站在水平地面上时对地面的压强约为1×104Pa。
14.(1)货车停下后对地面的压强为5×106Pa;
(2)货车匀速行驶10s牵引力做的功为6×106J。
【分析】(1)知道载重货车的总质量,利用重力的计算公式G=mg可以计算出其受到的总重力;载重货车对地面的压力等于其总重力,知道受力面积,利用公式p=求货车对地面的压强;
(2)由v=得车匀速行驶10s行驶的路程,根据阻力与重力的关系求出阻力,再根据二力平衡的条件求出牵引力的大小,利用W=Fs求得牵引力做的功。
【解答】解:(1)车的总质量:m总=5t+25t=30t=30000kg,
车受到的总重力:G=mg=30000kg×10N/kg=3×105N,
汽车对地面的压强p===5×106Pa;
(2)车匀速行驶10s行驶的路程s=vt=20m/s×10s=200m,
由二力平衡条件可得,汽车的牵引力F牵引力=f=0.1G=0.1×3×105N=30000N,
汽车牵引力所做的功W=F牵引力s=30000N×200m=6×106J。
答:(1)货车停下后对地面的压强为5×106Pa;
(2)货车匀速行驶10s牵引力做的功为6×106J。
15.1)空鱼缸对窗台的压强为500Pa;
(2)注水后鱼缸底部受到水的压强为1000Pa;
(3)抬高鱼缸的过程中,小明对鱼缸和水总共做的功为6J。
【分析】(1)知道鱼缸的重力;因为在水平桌面上,利用F=G求鱼缸对桌面的压力,再利用p=求鱼缸对桌面的压强;
(2)知道鱼缸内水深和水的密度,利用液体压强公式求水对鱼缸底的压强;
(3)求出鱼缸和水的总重力,根据W=Fs=Gh求出小明对鱼缸和水总共做的功。
【解答】解:(1)空鱼缸对桌面的压力:F=G=5N,
空鱼缸对窗台的压强:
p===500Pa;
(2)注水后鱼缸底部受到水的压强:
p′=ρgh=1×103kg/m3×10N/kg×10×10﹣2m=1000Pa;
(3)水和鱼缸的总重力:
G总=G+G水=G+m水g=5N+1.5kg×10N/kg=20N,
抬高鱼缸的过程中,小明对鱼缸和水总共做的功:
W=Fs=G总h=20N×0.3m=6J,
答:(1)空鱼缸对窗台的压强为500Pa;
(2)注水后鱼缸底部受到水的压强为1000Pa;
(3)抬高鱼缸的过程中,小明对鱼缸和水总共做的功为6J。
16.(1)注水过程中,“背漂”受到的最大浮力为30N。
(2)细线的长度15cm。
(3)注水过程中,浮力对“背漂”所做的功为0.225J。
【分析】(1)由图像知当“背漂”完全浸没时的拉力,此时受到的浮力最大,根据F浮最大=F+G算出最大浮力;
(2)“背漂”刚好漂浮时,浮力等于重力,计算水的深度,根据绳子刚开始有拉力的深度,计算物体上升的高度,即绳子的长度;
(3)根据细线的长度,即“背漂”上升的高度,然后根据功的计算公式求出“背漂”做的功。
【解答】解:(1)由图像知当“背漂”完全浸没时,拉力F=28.5N,受到的浮力最大,最大浮力为:
F浮最大=F+G=28.5N+1.5N=30N;
(2)“背漂”刚浮起来时,受到的浮力为:
F浮=G=1.5N,此时水的深度等于“背漂”浸没水中的深度,由F浮=ρ液gV排知“背漂”排开水的体积为:
V排===1.5×10﹣4m3=150cm3,
此时容器中水的深度为:
h===0.4cm;
当绳子刚好有拉力时,水的深度为15.4cm,则绳子的长度为15.4cm﹣0.4cm=15cm。
(3)细线的长度为L=15cm=0.15m,即在浮力作用下“背漂”向上移动的距离为s=L=0.15m,所以浮力对“背漂”做的功为:
W=F浮L=1.5N×0.15m=0.225 J。
答:(1)注水过程中,“背漂”受到的最大浮力为30N。
(2)细线的长度15cm。
(3)注水过程中,浮力对“背漂”所做的功为0.225J。
17.(1)物块的重力为30N;
(2)在2~4s内物块运动的平均速度为1m/s;
(3)在前6s内,拉力F做的功为42J。
【分析】(1)根据G=mg可求出物块的重力;
(2)在速度—时间图像中,物体运动的距离等于这段时间的图像与t轴之间的面积;由图丙求出在2~4s内物块运动的距离,根据v=求出其平均速度;
(3)根据图丙得出在0~2s内物块处于静止状态,从而得出拉力不做功;根据题意可知物块在2~4s的运动距离,根据W=Fs求出拉力F做的功;利用v=求出物块在4~6s内运动的距离,根据W=Fs求出拉力F做的功;然后求出前6s内拉力F做的功。
【解答】解:(1)物块的重力为G=mg=3kg×10N/k=30N;
(2)由图丙知,在2~4s内物块运动的距离等于这段时间的图像与t轴之间的面积,即s==2m,其平均速度v=;
(3)由图丙可知,在0~2s内,物块的速度为0处于静止状态,拉力不做功,W1=0;
由(2)可知,物块在2~4s的运动距离为s=2m,拉力F做的功W2=F2s=9N×2m=18J;
由图丙可知,物块在4~6s内以2m/s的速度做匀速直线运动,由v=可得,物块在4~6s内运动的距离s3=v3t3=2m/s×(6s﹣4s)=4m,
由图乙可知,物块在4~6s内受到的拉力为6N,
拉力F做的功W3=F3s3=6N×4m=24J;
所以,前6s内拉力F做的功W总=W1+W2+W3=0J+18J+24J=42J。
答:(1)物块的重力为30N;
(2)在2~4s内物块运动的平均速度为1m/s;
(3)在前6s内,拉力F做的功为42J。
【计算4 功率的计算及公式的应用】
18.(1)机器人受到的重力是0.12N;
(2)静止时,它对水平地面的压强是1200Pa;
(3)拉力的功率是11W。
【分析】(1)知道机器人的质量,利用重力公式求其重力;
(2)机器人对水平地面的压力等于重力,又知道受力面积,利用压强公式求机器人对地面的压强;
(3)由W=Fs计算拉力做的功,由P=计算拉力的功率。
【解答】解:拉力的功率
(1)微型机器人的重力:
G=mg=1.2×10﹣2kg×10N/kg=0.12N;
(2)机器人静止时,它对水平地面的压力F=G=0.12N,
对水平地面的压强:
p===1200Pa;
(3)拉力做的功:
W=Fs=110N×1m=110J,
拉力的功率:
P===11W。
答:(1)机器人受到的重力是0.12N;
(2)静止时,它对水平地面的压强是1200Pa;
(3)拉力的功率是11W。
19.(1)旦增过桥所用的时间为21s;
(2)大桥的长度为525m;
(3)列车过桥时所受阻力的大小为2×105N。
【分析】(1)根据图乙中的信息可求出旦增过桥所用的时间;
(2)已知列车过桥时速度和所用的时间,根据s=vt求出列车通过的路程,即为大桥的长度;
(3)根据P===Fv求出列车受到的牵引力,利用二力平衡条件求出列车过桥时所受阻力的大小。
【解答】解:(1)由图乙可知,旦增过桥所用的时间为t=9:35:41﹣9:35:20=21s;
(2)列车过桥时速度保持25m/s不变,则大桥的长度为:
s=vt=25m/s×21s=525m;
(3)列车功率约为5×106W,列车过桥时速度保持25m/s不变,
则根据P===Fv可知,列车受到的牵引力为:
F===2×105N,
因列车过桥时速度不变,且藏木特大桥平直,即列车过桥时做匀速直线运动,所以列车过桥时所受阻力与牵引力为一对平衡力,
由二力平衡条件可得,列车过桥时所受阻力为:f=F=2×105N。
答:(1)旦增过桥所用的时间为21s;
(2)大桥的长度为525m;
(3)列车过桥时所受阻力的大小为2×105N。
20.(1)货车匀速行驶1h,牵引力做的功是2.16×109J;
(2)车上坡时的速度是10m/s。
【分析】(1)由求出货车匀速行驶1h通过的路程,根据重力公式求出载重货车的总重力,根据阻力与总重力的关系求出阻力,再根据二力平衡的条件求出牵引力的大小,再利用W=Fs求得牵引力做的功;
(2)整个过程中货车的功率不变,货车上坡时的牵引力需增大为水平路面的2倍,利用公式P=Fv求出车上坡时的速度。
【解答】解:(1)货车匀速行驶1h通过的路程:s=vt=20m/s×3600s=7.2×104m,
载重货车的总重力:G总=m总g=(m车+m货)g=(5+25)×103kg×10N/kg=3×105N,
由二力平衡条件可得,汽车的牵引力:F牵=f=0.1G总=0.1×3×105N=3×104N,
汽车牵引力所做的功:W=F牵s=3×104N×7.2×104m=2.16×109J;
(2)因为,行驶过程中货车的功率始终保持不变,所以P1=P2,则有F1v1=F2v2,
货车上坡时的牵引力增大为水平路面时的2倍(即F2=2F1),则车上坡时的速度:
。
答:(1)货车匀速行驶1h,牵引力做的功是2.16×109J;
(2)车上坡时的速度是10m/s。
21.(1)观光艇满载时,所受浮力是1.2×104N;
(2)观光艇以最大速度航行时,受到水的平均阻力是4×103N;航行2km,发动机做功8×106J;
(3)水对艇底部的压强为5×103Pa。
【分析】(1)从技术参数表得出观光艇和8人总质量,利用重力公式求人、观光艇总重力,再利用漂浮条件求观光艇满载时,所受水的浮力;
(2)从技术参数表得出发动机的最大功率,利用P===Fv的变形公式F=求牵引力;又因为观光艇匀速行驶,受平衡力,据此求受到水的平均阻力;由W=Fs可知发动机做功多少;
(3)利用p=ρgh求得水对艇底部的压强。
【解答】解:(1)观光艇满载时观光艇和8人总质量为:
m=800kg+50kg×8=1200kg,
满载时人、观光艇总重力为:
G=mg=1200kg×10N/kg=1.2×104N,
观光艇漂浮,观光艇满载乘客时所受浮力为:F浮=G=1.2×104N;
(2)P===Fv,则观光艇受到的牵引力为:
F===4×103N,
观光艇匀速行驶,故观光艇受到的牵引力和水的阻力为平衡力,
观光艇受到水的平均阻力为:
f=F=4×103N;
航行2km,发动机做功:W=Fs=4×103N×2×103m=8×106J;
(3)由p=ρ水gh可知当吃水达到该位置时,水对艇底部的压强为:
p=ρ水gh=1.0×103kg/m3×10N/kg×50×10﹣2m=5×103Pa。
答:(1)观光艇满载时,所受浮力是1.2×104N;
(2)观光艇以最大速度航行时,受到水的平均阻力是4×103N;航行2km,发动机做功8×106J;
(3)水对艇底部的压强为5×103Pa。
22.(1)第一次下潜到8000米时海斗号所受海水的压强为8×107Pa;
(2)此时观测孔所受海水的压力为3.2×106N;
(3)浮力做功的功率为3×105W,海斗号所受海水的阻力为2.5×105N。
【分析】(1)根据p=ρ液gh求出第一次下潜到8000米时海斗号所受海水的压强;
(2)知道海斗号下潜到8000米后所受海水的压强和观测孔的面积,根据F=pS求出此时观测孔所受海水的压力;
(3)海斗号匀速直线上升返回海面时排开海水的体积和自身的体积相等,根据F浮=ρ液gV排求出海斗号所受的浮力,利用P===Fv求出浮力做功的功率;对海斗号进行受力分析,根据海斗号受到的合力为零得出等式即可求出海斗号所受海水的阻力。
【解答】解:(1)第一次下潜到8000米时海斗号所受海水的压强:p=ρ海水gh=1×103kg/m3×10N/kg×8000m=8×107Pa;
(2)观测孔的面积:S=4dm2=4×10﹣2m2,
由p=可得,此时观测孔所受海水的压力:F=pS=8×107Pa×4×10﹣2m2=3.2×106N;
(3)因物体浸没时排开液体的体积和自身的体积相等,
所以,海斗号所受的浮力:F浮=ρ海水gV排=ρ海水gV=1×103kg/m3×10N/kg×60m3=6×105N,
浮力做功的功率:P===F浮v=6×105N×0.5m/s=3×105W;
因海斗号匀速直线上升返回海面时,受到竖直向上的浮力和竖直向下的重力、阻力作用处于平衡状态,
由海斗号受到的合力为零可得:F浮=G+f=mg+f,
则海斗号所受海水的阻力:f=F浮﹣mg=6×105N﹣35×103kg×10N/kg=2.5×105N。
答:(1)第一次下潜到8000米时海斗号所受海水的压强为8×107Pa;
(2)此时观测孔所受海水的压力为3.2×106N;
(3)浮力做功的功率为3×105W,海斗号所受海水的阻力为2.5×105N。
23.(1)物体B下降的速度是0.1m/s;
(2)水平面对物体A的摩擦力是12N;
(3)要使物体B恰好以0.2m/s的速度匀速上升,则要对物体A施加水平向右拉力F的功率为9.6W。
【分析】(1)根据v=算出物体B下降的速度;
(2)由图知,有2段绳子承担物重,即n=2,不计绳重、绳子的伸长和滑轮组内部的摩擦,当物体B匀速下降时,物体A受到水平向右滑动摩擦力的大小f=F拉=(GB+G动);
(3)当物体B匀速上升时,处于平衡状态,受平衡力的作用,对物体A施加水平向右的拉力等于向左的摩擦力加上滑轮组绳子自由端拉力,由于有2段绳子承担物重,所以物体A向右运动的速度等于物体B上升速度的2倍,利用P===Fv求拉力F的功率。
【解答】解:
(1)物体B下降的速度为:
vB===0.1m/s;
(2)由图知,有2段绳子承担物重,即n=2,不计绳重、绳子的伸长和滑轮组内部的摩擦,当物体B匀速下降时,物体A受到水平向右滑动摩擦力的大小为:
f=F拉=(GB+G动)=×(20N+4N)=12N;
(3)当物体B匀速上升时,绳子的拉力F拉不变,由于物体A受到的压力和接触面的粗糙程度不变,所以物体A受到的摩擦力大小不变,仍为12N,
由力的平衡条件可得,对物体A施加水平向右的拉力:
F=f+F拉=12N+12N=24N,
物体A向右运动的速度:
vA=2vB′=2×0.2m/s=0.4m/s,
拉力F的功率:
P===FvA=24N×0.4m/s=9.6W。
答:(1)物体B下降的速度是0.1m/s;
(2)水平面对物体A的摩擦力是12N;
(3)要使物体B恰好以0.2m/s的速度匀速上升,则要对物体A施加水平向右拉力F的功率为9.6W。
【计算5 机械效率的计算】
24.(1)桩锤对桩的压强是1×107Pa;
(2)①此过程中的有用功为8×103J;
②此过程中打桩机的机械效率为50%。
【分析】(1)已知压力和受力面积,根据压强公式P=,可求出桩锤对桩的压强;
(2)利用W有=Gh=mgh求出卷扬机克服重力做的功;
利用W总=Pt求出总功,根据效率公式η=×100%可求出卷扬机的效率。
【解答】解:(1)桩锤对桩的压强是:
P===1×107Pa;
(2)①卷扬机克服重力做的有用功是:
W有=Gh=mgh=400kg×10N/kg×2m=8×103J;
②卷扬机做的总功是:
W总=Pt=8×103W×2s=1.6×104J,
卷扬机的效率是:
η=×100%=×100%=50%。
答:(1)桩锤对桩的压强是1×107Pa;
(2)①此过程中的有用功为8×103J;
②此过程中打桩机的机械效率为50%。
25.(1)水箱中水的质量是2×103kg;
(2)抽水机抽水过程中对水做的有用功2.4×105J;
(3)抽水机抽水时的效率是80%。
【分析】(1)已知水的密度与水箱的容积,由密度公式求出水的质量;
(2)根据重力公式求出水的重力,再根据W=Gh求出抽水机所做的功;
(3)根据机械效率公式抽水机的效率。
【解答】解:(1)根据ρ=可得水箱中水的质量:
m=ρV=1.0×103kg/m3×2m3=2×103kg;
(2)水的重力:G=mg=2×103kg×10N/kg=2×104N,
抽水机抽水过程中对水做的有用功:
W有用=Gh=2×104N×12m=2.4×105J;
(3)抽水机抽水时的效率:
η==×100%=×100%=80%。
答:(1)水箱中水的质量是2×103kg;
(2)抽水机抽水过程中对水做的有用功2.4×105J;
(3)抽水机抽水时的效率是80%。
26.(1)电动机对绳子的拉力为750N;
(2)电动机对吊篮(包括人及工具)做的功为1.8×104J,功率为600W;
(3)对吊篮做的功为额外功,对人和工具做的功为有用功,则机械效率是80%。
【分析】(1)不计滑轮重、绳重和摩擦,根据F=G总求出电动机对绳子的拉力;
(2)求出绳子自由端移动的距离s=nh,根据W=Fs求出电动机对吊篮(包括人及工具)做的功,即总功;根据P=求出电动机对吊篮(包括人及工具)做功的功率;
(3)根据=Gh求出有用功,根据η=求出机械效率。
【解答】解:(1)由题图可知,绳子承重股数为n=4,不计滑轮重、绳重和摩擦,电动机对绳子的拉力为:F=G总=m总g=×(60kg+240kg)×10N/kg=750N;
(2)绳子自由端移动的距离为:s=nh=4×6m=24m,
电动机对吊篮(包括人及工具)做的功,即总功为:W总=Fs=750N×24m=1.8×104J;
电动机对吊篮(包括人及工具)做功的功率为:P==600W;
(3)有用功为:W有=Gh=mgh=240N×10N/kg×6m=1.44×104J;
机械效率为:η==80%。
答:(1)电动机对绳子的拉力为750N;
(2)电动机对吊篮(包括人及工具)做的功为1.8×104J,功率为600W;
(3)对吊篮做的功为额外功,对人和工具做的功为有用功,则机械效率是80%。
27.(1)移送泥土的过程中,挖掘机对泥土所做的功为4.8×104J;
(2)挖掘机的机械效率为60%;
(3)挖掘机所做的额外功可将500N的物体抬高64米。
【分析】(1)移送泥土的过程中,挖掘机对泥土所做的功,是指对泥土的重力做功,那么在重力的方向上移动的距离是最大挖掘深度和最大卸料高度之和,然后利用W=Gh即可求出挖掘机对泥土所做的功;
(2)先根据发动机的总功率是20kW求出挖掘机在4s内做的总功,再利用η=×100%.即可求出此过程挖掘机的机械效率;
(3)先计算出额外功,利用W=Gh计算将泥土提高的高度。
【解答】解:(1)满斗泥土所受重力:G=mg=600kg×10N/kg=6000N,
对泥土做功:W有=G泥h=6000N×(3m+5m)=4.8×104J;
(2)由P=得,挖掘机的发动机4s内做的总功:W总=Pt=2×104W×4s=8×104J;
挖掘机的机械效率:η=×100%=×100%=60%;
(3)挖掘机所做额外功:W额=W总﹣W有=8×104J﹣4.8×104J=3.2×104J,
由W=Gh得,可将500N的物体抬高高度:h′===64m。
答:(1)移送泥土的过程中,挖掘机对泥土所做的功为4.8×104J;
(2)挖掘机的机械效率为60%;
(3)挖掘机所做的额外功可将500N的物体抬高64米。
【计算6 滑轮(组)的机械效率】
28.(1)图中金属块静放在地面时对地面的压强为;
(2)拉力在使用滑轮的过程中做的总功为2F2L;
(3)该滑轮的机械效率为。
【分析】(1)金属块静止放在水平路面上时对地面的压力和自身的重力相等,利用p=求出金属块静放地面时对地面的压强;
(2)动滑轮绳子的有效股数为2,根据s=nL求出绳端移动的距离,利用W=Fs求出拉力做的总功;
(3)两种方式拉金属块时,金属块受到地面的摩擦力不变,用滑轮拉的过程中所做的有用功就是克服地面给金属块摩擦力所做的功,根据二力平衡条件求出受到的摩擦力,利用W=fL求出拉力在使用滑轮的过程中做的有用功;动滑轮的机械效率等于有用功题意总功之比。
【解答】解:(1)金属块静放在水平路面上时对地面的压力:F=G=mg,
金属块对地面的压强p==;
(2)动滑轮绳子的有效股数n=2,则绳端移动的距离s=nL=2L,
拉力做的总功W总=F2s=F2×2L=2F2L;
(3)因两种方式拉金属块时,金属块受到地面的摩擦力不变,用滑轮拉的过程中所做的有用功就是克服地面给金属块摩擦力所做的功,
因左图中金属块匀速直线运动时处于平衡状态,受到的摩擦力和绳子的拉力是一对平衡力,
所以,金属块受到的摩擦力f=F1,
所以,在使用滑轮的过程中拉力做的有用功W有=fL=F1L;
该滑轮的机械效率η===。
答:(1)图中金属块静放在地面时对地面的压强为;
(2)拉力在使用滑轮的过程中做的总功为2F2L;
(3)该滑轮的机械效率为。
29.(1)绳子自由端移动的距离8m;
(2)此过程中所做的额外功80J;
(3)此过程中所做的有用功720J;
(4)机械效率90%
【分析】(1)动滑轮绳子的有效股数为2,根据s=nh求出绳子自由端移动的距离;
(2)根据W额=G动h求出额外功的大小;
(3)根据W有=Gh求出有用功的大小;
(4)根据W总=W有+W额求出总功,根据机械效率公式求出机械效率的大小。
【解答】解:
(1)由图可知,n=2,物体上升h=4m,则绳子自由端移动的距离为:s=nh=2×4m=8m;
(2)由题意可知,不计绳重和摩擦,则此过程中所做的额外功为:W额=G动h=20N×4m=80J;
(3)此过程中所做的有用功为:W有=Gh=180N×4m=720J;
(4)总功为:W总=W有+W额=720J+80J=800J;
机械效率为:η==×100%=90%。
答:(1)绳子自由端移动的距离8m;
(2)此过程中所做的额外功80J;
(3)此过程中所做的有用功720J;
(4)机械效率90%。
30.(1)实心长方体浸没时受到的浮力为100N;
(2)实心长方体从水底到露出水面前,上升的高度为1.6m;
(3)实心长方体从水底到露出水面前,若人对绳的拉力F2做功400J,此过程中滑轮组的机械效率为80%。
【分析】(1)由图乙可知,物体浸没时,测力计示数F1=200N,当物体被拉出水面后,物体所受的拉力等于物体的重力,为G=300N,根据F浮=G﹣F1得出物体浸没在水中所受到的浮力;
(2)长方体从水底到刚好露出水面的运动时间为t=8s,根据h=vt得出长方体上升的高度;
(3)实心长方体从水底到露出水面前,根据W有用=F1h得出有用功,根据η=×100%得出此过程中滑轮组的机械效率。
【解答】解:(1)由图乙可知,物体浸没时,测力计示数F1=200N,
当物体被拉出水面后,物体所受的拉力等于物体的重力,为G=300N,
所以物体浸没在水中所受到的浮力为F浮=G﹣F1=300N﹣200N=100N;
(2)长方体从水底到刚好露出水面的运动时间为t=8s,
则长方体上升的高度为h=vt=0.2m/s×8s=1.6m;
(3)实心长方体从水底到露出水面前,有用功为W有用=F1h=200N×1.6m=320J,
此过程中滑轮组的机械效率为η=×100%=×100%=80%。
答:(1)实心长方体浸没时受到的浮力为100N;
(2)实心长方体从水底到露出水面前,上升的高度为1.6m;
(3)实心长方体从水底到露出水面前,若人对绳的拉力F2做功400J,此过程中滑轮组的机械效率为80%。
31.(1)绳子自由端移动的距离为6m,动滑轮的重为50N;
(2)工人做的有用功为1050J;
(3)工人做的额外功为150J;
(4)滑轮组的的机械效率为87.5%。
【分析】(1)根据滑轮组装置确定绳子股数,利用s=nh求出绳子自由端移动的距离;忽略摩擦及绳重,根据F=(G+G动)求出动滑轮的重;
(2)根据W有=Gh求出工人做的有用功;
(3)根据W总=Fs求出工人做的总功,利用W总=W有+W额求出额外功;
(4)根据η=求出滑轮组的的机械效率。
【解答】解:(1)由图可知,n=2,S=nh=2×3m=6m;
忽略摩擦及绳重,根据F=(G+G动)可知,动滑轮的重为:
G动=nF﹣G=2×200N﹣350N=50N;
(2)W有=Gh=350N×3m=1050J;
(3)W总=Fs=200N×6m=1200J,
W 额=W总﹣W有=1200J﹣1050J=150J;
(4)滑轮组的的机械效率为:
η=×100%=×100%=87.5%。
答:(1)绳子自由端移动的距离为6m,动滑轮的重为50N;
(2)工人做的有用功为1050J;
(3)工人做的额外功为150J;
(4)滑轮组的的机械效率为87.5%。
32.(1)动滑轮的重力G动为30N;
(2)当G物=120N时,若此时人在10s内将物体提升了2m,则此时拉力的功率为30W;
(3)若人站的位置能承受的最大压强为12500Pa,则该滑轮组所能提升物体的最大机械效率为90%
【分析】(1)不计绳重和摩擦,滑轮组的机械效率η=×100%=×100%=×100%=×100%,则动滑轮重G动=﹣G物;
(2)图乙中连接动滑轮的绳子股数n=3,不计绳重和摩擦,根据F′=×(G物′+G动)计算此时的拉力,根据W=Fs求出功的大小,根据P=求出功率的大小;
(3)当人站的位置承受的压强最大时,人对地面的压力最大,根据F压=pS计算,地面对人的支持力和人对地面的压力是相互作用力,大小相等,根据G=mg计算人的重力,人对绳的最大拉力F″=F支﹣G人,物体的最大重力G″=nF″﹣G动,滑轮组的最大机械效率根据η″=×100%计算。
【解答】解:(1)不计绳重和摩擦,滑轮组的机械效率η=×100%=×100%=×100%=×100%,则动滑轮重G动=﹣G物,
由图乙可知动滑轮的重力G动=﹣G物=﹣120N=30N;
(2)由图知,n=3,故自由端拉力为
自由端移动的距离为:s=3h=3×2m=6m;
拉力做的功为:W总=Fs=50N×6m=300J;
拉力的功率为:;
(3)人对地面的最大压力为:
地面对人的支持力等于人对地面的压力,即:F支=F压=500N;
人的重力为:G=m人g=40kg×10N/kg=400N,
故绳子的最大拉力为:Fm=F支﹣G=500N﹣400N=100N;
最大物重为Gm=3Fm﹣G动=3×100N﹣30N=270N;
此时机械效率最大,为:。
答:(1)动滑轮的重力G动为30N;
(2)当G物=120N时,若此时人在10s内将物体提升了2m,则此时拉力的功率为30W;
(3)若人站的位置能承受的最大压强为12500Pa,则该滑轮组所能提升物体的最大机械效率为90%。
33.(1)文物浸没在水中时受到的浮力是1×103N;
(2)动滑轮的重力是200N;
(3)在整个打捞过程中,a、b、c三根绳中a绳承受的拉力最大,该绳至少要承受5.1×103N的拉力。
【分析】(1)知道文物的体积,即浸没水中排开水的体积,利用阿基米德原理求文物受到的浮力;
(2)绳重、滑轮与轴的摩擦以及水的阻力均忽略不计,根据W有用=(G﹣F浮)h可求物体的重力G,再根据滑轮组的机械效率η===,据此求动滑轮重力;
(3)整个打捞过程中,若文物出水后,由图知,n=2,拉力F=(G+G动),即b根绳子承受的拉力;a点绳子的拉力Fa=2F+G定;c点绳子的拉力Fc=G;据此确定a、b、c三根绳中哪根绳承受的拉力最大及其大小。
【解答】解:
(1)文物浸没在水中时排开水的体积:
V排=V=100dm3=0.1m3,
则文物受到的浮力:
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×0.1m3=1×103N;
(2)因绳重、滑轮与轴的摩擦以及水的阻力均忽略不计,
由W有用=(G﹣F浮)h可得,物体的重力:
G=+F浮=+1×103N=4.8×103N,
则文物完全浸没在水中时,滑轮组的机械效率:
η====95%,
即:=95%,
解得动滑轮重力:G动=200N;
(3)整个打捞过程中,若文物出水后,
由图知,n=2,绳子自由端的拉力:
F=(G+G动)=×(4.8×103N+200N)=2.5×103N,
即b绳承受的拉力:Fb=F=2.5×103N;
a绳承受的拉力:Fa=2F+G定=2×2.5×103N+100N=5.1×103N;
c绳承受的拉力:Fc=G=4.8×103N;
可见,a、b、c三根绳中a绳承受的拉力最大,该绳至少要承受5.1×103N的拉力。
答:(1)文物浸没在水中时受到的浮力是1×103N;
(2)动滑轮的重力是200N;
(3)在整个打捞过程中,a、b、c三根绳中a绳承受的拉力最大,该绳至少要承受5.1×103N的拉力。
【计算7 杠杆的机械效率】
34.(1)杠杆自重为15N。
(2)杠杆提升重物的机械效率约为66.7%。
(3)若将动力作用点从B点移到C点,其它条件不变,杠杆的机械效率不变。
【分析】(1)根据杠杆的平衡条件算杠杆自重;
(2)根据公式η=计算效率;
(3)先算出改变后的效率,再进行比较。
【解答】解:(1)杠杆水平放置时,杠杆自重的力臂L3=OC;
设OA=L0,则OB=3L0,OC=4L0,故L3=OC=×4L0=2L0;
根据杠杆平衡条件可知:F OB=G OA+G杆L3;
F×3L0=60N×L0+G杆×2L0;
故3F=60N+2G杆;
解得:G杆=15N;
(2)因为OA:OB=1:3,故B点上升的高度是A点的3倍,
故机械效率为:
η===≈66.7%;
(3)若将动力作用点从B点移到C点时,因为OA:L3=1:2,所以杠杆重心上升的高度是物体上升高度的2倍;故:
η====≈66.7%;
答:(1)杠杆自重为15N。
(2)杠杆提升重物的机械效率约为66.7%。
(3)若将动力作用点从B点移到C点,其它条件不变,杠杆的机械效率不变。
35.(1)力F的大小为90N;
(2)将重物匀速提升时杠杆的机械效率为83.3%。
【分析】由题意可知,将挂在杠杆中点B的物体匀速缓慢提升至虚线位置时,这个过程中阻力臂与动力臂的比值始终等于杠杆在水平位置时阻力臂与动力臂的比值,知道动力臂、阻力臂、阻力,根据杠杆平衡条件F1×L1=F2×L2求出动力F;
由W=Gh可求得有用功,由W总=Fs可求得总功,由η=×100%可求得杠杆的机械效率。
【解答】解:用竖直向上的拉力F在A点,将挂在杠杆中点B的重为150N的物体匀速缓慢提升至虚线位置时,杠杆自身重力的作用点在中点,这个过程中阻力臂与动力臂的比值始终等于杠杆在水平位置时阻力臂与动力臂的比值,即比值始终为=,由杠杆平衡条件可得,F×L1=(G+G杆)×L2可知,竖直向上提升过程中动力F大小不变,
F×OA=(G+G杆)×OB可得,
F====90N;
此时杠杆所做的有用功W有用=Gh=150N×0.5m=75J,
此时杠杆所做的总功W总=Fs=90N×1m=90J,
杠杆的机械效率:
η=×100%=×100%≈83.3%。
答:(1)力F的大小为90N;
(2)将重物匀速提升时杠杆的机械效率为83.3%。
36.200;70。
【分析】(1)根据公式W=Fs可求总功;
(2)根据公式W=Gh可求有用功,有用功与总功的比值就是千斤顶的机械效率。
【解答】解:
(1)人做的功是总功:W总=Fs=100N×2m=200J;
(2)已知h=14cm=0.14m,所做的有用功:
W有用=Gh=1000N×0.14m=140J,
千斤顶的机械效率:
η=×100%=×100%=70%。
故答案为:200;70。
【计算8 斜面的机械效率】
37.(1)汽车从山底开到山顶所做的有用功为1.5×107J;
(2)山坡的机械效率为30%;
(3)汽车在山坡上行驶时的摩擦力为1.75×104N。
【分析】(1)利用W=Gh求汽车从山底开到山顶所做的有用功;
(2)利用W=Fs算出牵引力做的总功,山坡的机械效率等于有用功与总功之比;
(3)额外功等于总功减去有用功,再利用W额=fs求汽车在山坡上行驶时的摩擦力。
【解答】解:(1)货车从山底到山顶牵引力做的有用功:
W有用=Gh=5.0×104N×300m=1.5×107J;
(2)汽车从山底开到山顶所做的总功为:
W总=Fs=2.5×104N×2000m=5×107J;
山坡的机械效率为:
η==×100%=30%;
(3)货车上坡时所做的额外功,即克服摩擦力做的功为:
W摩=W总﹣W有用=5.0×107 J﹣1.5×107 J=3.5×107J,
由W额=fs可得,汽车在山坡上行驶时的摩擦力为:
货车上坡时的摩擦力f===1.75×104 N;
答:(1)汽车从山底开到山顶所做的有用功为1.5×107J;
(2)山坡的机械效率为30%;
(3)汽车在山坡上行驶时的摩擦力为1.75×104N。
38.(1)绳子拉力F对A所做的有用功为600J;
(2)该斜面的机械效率为80%;
(3)物体A受到的滑动摩擦力为30N。
【分析】(1)知道物体的重力、斜面高,根据W=Gh求绳子拉力F对物体A所做的有用功;
(2)由图知,n=2,不计绳重、滑轮与绳间的摩擦力、空气阻力,使用滑轮组的绳子自由端的拉力F=(GB+G动),力的作用是相互的,可求绳对A的拉力的大小,知道斜面长,根据W=Fs求出拉力对A所做的总功;斜面的机械效率等于有用功与总功之比;
(3)根据公式W额=W总﹣W有用求出额外功,在拉动物体A的过程中克服摩擦力做的功是额外功,根据公式W额=fs求出摩擦力的大小。
【解答】解:(1)绳子拉力F对物体A所做的有用功:W有用=GAh=200N×3m=600J,
(2)由图可知,物体A用细绳跨过滑轮组与物体B连起来,在动滑轮与重物B的作用下,能够使物体A由斜面底端被匀速拉到顶端,
不计绳重、滑轮组内部摩擦及空气阻力,对A的拉力大小等于使用滑轮组绳子自由端的拉力:
F=(GB+G动)=×(280N+20N)=150N;
拉力对A做的总功:W总=Fs=150N×5m=750J,
斜面机械效率:η=×100%=×100%=80%;
(3)拉力对物体A做的额外功:W额=W总﹣W有用=750J﹣600J=150J,
由W额=fs可得,A与斜面间的摩擦力大小为:
f===30N。
答:(1)绳子拉力F对A所做的有用功为600J;
(2)该斜面的机械效率为80%;
(3)物体A受到的滑动摩擦力为30N。
39.(1)斜面对木块的摩擦力为90N;
(2)斜面的机械效率是62.5%。
【分析】(1)斜面是用来提高物体位置的,有用功等于物体重力和斜面高度的乘积。
总功等于物体沿斜面向上的拉力和斜面长的乘积。
求出额外功,利用W额=fs求摩擦力。
(2)机械效率就是有用功和总功的比值。
【解答】解:(1)斜面是与水平面成30度的角,
h=L=×5m=2.5m,
W有用=Gh=300N×2.5m=750J,
总功W总=FL=240N×5m=1200J,
W额=W总﹣W有用=1200J﹣750J=450J,
f===90N;
(2)机械效率η=×100%=×100%=62.5%。
答:(1)斜面对木块的摩擦力为90N;
(2)斜面的机械效率是62.5%。
40.(1)箱子受到的重力为300N;
(2)箱子受到的摩擦力为30N;
(3)斜面的机械效率为80%;
(4)减小斜面的坡度、减小斜面的粗糙程度,都可以省力。
【分析】(1)知道箱子的质量,利用G=mg求箱子受到的重力;
(2)利用W=Fs求推力所做的总功,利用W=Gh求推力做的有用功,沿斜面推动箱子,克服斜面对箱子的摩擦力做的功是额外功,其大小等于总功减去有用功,再利用W额=fs求箱子受到的摩擦力;
(3)斜面的机械效率等于有用功与总功之比;
(4)使用斜面时,在斜面高一定时,斜面越长越省力;减小斜面的粗糙程度可以省力。
【解答】解:(1)箱子受到的重力:
G=mg=30kg×10N/kg=300N;
(2)推力所做的总功:W总=Fs=150N×3m=450J,
推力做的有用功:W有用=Gh=300N×1.2m=360J,
沿斜面推动箱子,克服斜面对箱子的摩擦力做的功是额外功,其大小为:
W额=W总﹣W有=450J﹣360J=90J,
由W额=fs可得箱子受到的摩擦力:
f===30N;
(3)斜面的机械效率:η=×100%=×100%=80%;
(4)减小斜面的坡度、减小斜面的粗糙程度,都可以省力。
答:(1)箱子受到的重力为300N;
(2)箱子受到的摩擦力为30N;
(3)斜面的机械效率为80%;
(4)减小斜面的坡度、减小斜面的粗糙程度,都可以省力。
专题03简单机械和功(实验专题训练)
【计算1杠杆的平衡条件】
1.巴南区某学校在开展物理兴趣小组活动时,学生为深入探究平衡木的平衡,小萍设计了如图所示的装置。轻质杠杆AOB可绕支点O无摩擦转动,且AB=3m,OA=1m。在杠杆A端用不可伸长的细线悬挂正方体M,质量为40kg,边长为20cm。当重为500N的小萍静止站立在OB之间某处时,正方体M对地面压力刚好为0,杠杆同时在水平位置处于平衡状态。求:
(1)正方体M的重力;
(2)当正方体M对地面压力刚好为0时,小萍距O点的距离;
(3)如果小萍站立在距离B端1.5m处时,正方体M对水平地面的压强。
2.杆秤是我国古老且至今仍在使用的一种衡量工具,如图的杆秤可视为杠杆,提纽处为支点O,若不计其自重,当在挂钩悬挂被称物体后处于平衡状态,已知CO=2厘米,OD=20厘米,秤砣的重力为10牛,求:
(1)被称物体的重力;
(2)若这杆秤所能测物体的最大重力为200牛,求OB的长度。
3.如图所示是锅炉保险阀门的示意图。当阀门受到的蒸汽压力超过其安全值时,阀门就会被拉开。其中OB=1m,OA=0.25m,阀门的底面积为2cm2,锅炉内气体压强的安全值为6×105Pa,杠杆的重力、摩擦均不计,锅炉外的大气压p0=1×105Pa。求:
(1)当阀门刚好被拉开时,蒸汽对阀门向上的压力;
(2)当阀门刚好被拉开时,A点受到的压力大小;
(3)B点所挂重物的重力大小。
4.如图所示,一个重为20N、边长为10cm的实心正方体M,悬挂在轻质杠杆B端,OB:OA=5:4,当M的一半体积浸在水中时,在A端施加一个竖直向下的拉力F使杠杆在水平位置平衡。(水的密度为1.0×103kg/m3,g取10N/kg)求:
(1)M底部受到的水对它的压强;
(2)M受到的水对它的浮力;
(3)F的大小。
5.小明发现一个不吸水的新型圆台体建筑材料,测得其重力为12N。他用弹簧测力计和杠杆设计了如图所示的装置进行实验,轻质杠杆OB可绕O点转动,圆台体材料用细绳悬挂在杠杆上A点,容器M中装有水并置于水平地面,当杠杆在水平位置平衡时B端竖直向上的拉力F为0.5N,此时圆台体材料浸没在水中静止且未触底。已知ρ水=1.0×103kg/m3,g取10N/kg,求:
(1)当轻质杠杆在水平位置平衡时,细绳对圆台体材料的拉力;
(2)当轻质杠杆在水平位置平衡时,圆台体材料受到的浮力;
(3)圆台体材料的密度。
6.如图甲所示,MN是以O为支点的轻质杠杆,OM:ON=4:1,物体A是棱长为10cm的实心均匀正方体,将A自由放置在底面积为200cm2的薄壁柱形容器中,在A的正上方是一个质量为1kg、底面积为60cm2、高为10cm的长方体B,用轻质细杆分别将B和C竖直连接在杠杆M、N两端,且杠杆在水平位置平衡,C是重为100N,边长为10cm的实心均匀正方体。现向容器中注水,物体A所受的浮力F与水的深度h的变化关系如图乙所示。求:
(1)A的质量;
(2)未向容器中注水时,C对水平地面的压强;
(3)当C对地面的压强为8800Pa时,向容器中一共注入水的质量。
【计算2 滑轮组中的相关计算】
7.如图所示,利用滑轮组装置匀速拉动水平面上质量是10千克的物体,已知物体在水平面上受到的滑动摩擦力为重力的0.1倍,动滑轮重2N,物体被拉动的速度是0.1米/秒,不计绳重和绳与滑轮间的摩擦力。g=10N/kg,求:
(1)物体在水平面上受到的滑动摩擦力是多少?
(2)拉力F的大小是多少?
(3)拉力F在10秒内移动的距离是多少?
8.如图所示,质量为60kg的工人用滑轮组吊起质量为40kg的箱子,(忽略绳重、摩擦和动滑轮重力),求:
(1)物体的重力。
(2)工人所施加的拉力大小。
(3)通过计算说明,该工人用此装置能否拉起重为1400N的物体?
9.小明同学用如图所示的滑轮组用时10s匀速提升质量20kg的物体,物体向上移动了2m,不计绳重和摩擦,g取10N/kg,动滑轮重力为20N。求:
(1)所提物体的重力;
(2)作用在绳子自由端的拉力;
(3)绳子自由端的移动速度。
10.质量为60kg的边长为50cm正方形水泥板平放在水平地面上,现要在10s内用如图所示装置将水泥板匀速升到离地面10m高处,动滑轮重力为20N,不考虑绳子与轮的摩擦。求:(g=10N/kg)
(1)人收绳的速度;
(2)人的拉力;
(3)当水泥板单独放在水平地面时,对地面的压强为多大?
11.某校科技小组,设计了如图所示的一套从水中打捞物体的简单滑轮组装置,动滑轮的重力为50N,物体A的质量为60kg,体积为0.04m3;通过滑轮组把A从水中匀速提升,不计绳重、摩擦及水的阻力,ρ水=1×103kg/m3。求:
(1)A浸没在水中所受浮力;
(2)A露出水面前,绳子自由端的拉力;
(3)若人的重力为625N,与水平地面的接触面积为500cm2,物体A出水后,求人对地面的压强。
【计算3 功的计算和公式的应用】
12.“绿水青山就是金山银山”,为了保护环境,我国大力发展电动汽车替代传统燃油汽车。表中是某种电动汽车的部分参数,假设车上只有司机一人,质量为60kg,汽车在水平公路匀速行驶时所受阻力为总重力的0.04倍,电动汽车充满电后以最高速度匀速行驶60km。(g=10N/kg)求:
空车质量 1340kg
轮胎与地面总接触面积 320cm2
电池容量 42kW h
最高速度 120km/h
(1)行驶这段路程所用的时间;
(2)电动汽车在水平公路匀速行驶时牵引力的大小;
(3)电动汽车匀速行驶60km,牵引力所做的功。
13.如图是小伟同学在单杠上做引体向上时的情景,每次引体向上身体上升的高度为0.6m,求解下列问题。(小伟的质量为50kg,g取10N/kg)
(1)引体向上前小伟先进行了热身训练,他绕操场跑了600m用时5min,求他热身运动的平均速度。
(2)小伟的体重是多少?
(3)小伟完成1次引体向上克服重力做的功。
(4)小伟做完引体向上运动后,双脚稳稳地站在水平地面上,请你计算他此时对地面的压强。(小伟每个鞋底的底面积为250cm2)
14.一质量为5t的载重货车,现装有质量为25t的货物以20m/s的速度匀速行驶在水平公路上,已知货车共有4个车轮,每个车轮与地面接触面积为1.5dm2,汽车匀速行驶时,受到的阻力是总重的0.1倍,求:
(1)货车停下后对地面的压强;
(2)货车匀速行驶10s牵引力做的功。
15.重为5N的空鱼缸,放在水平窗台上,其底面与窗台的接触面积为0.01m2,如图,向鱼缸内注入1.5kg的水,水的深度为10cm。假设小明沿竖直方向把盛水的鱼缸匀速抬高0.3m。(g取10N/kg,水的密度为1.0×103kg/m3)求:
(1)空鱼缸对窗台的压强;
(2)注水后鱼缸底部受到水的压强;
(3)抬高鱼缸的过程中,小明对鱼缸和水总共做的功。
16.“背漂”是儿童游泳时常佩戴的一种救生装置。某款长方体“背漂”重为1.5N,底面积为375cm2。把足够大的柱形容器放在水平台面上,用不可伸长的细线一端与“背漂”的底面相连,另一端固定在容器底部,如图甲。往容器中缓慢持续注水,注水过程中细线的拉力F与水的深度h的关系如图乙所示,求:
(1)注水过程中,“背漂”受到的最大浮力;
(2)细线的长度;
(3)注水过程中,浮力对“背漂”所做的功。
17.如图甲所示,质量为3kg的物块,在拉力F的作用下在水平面上做直线运动。拉力随时间变化、速度随时间变化图象分别如图乙、丙所示,已知物块在0~6s的运动距离为6m。求(g取10N/kg):
(1)物块的重力;
(2)在2~4s内物块运动的平均速度;
(3)在前6s内,拉力F做的功。
【计算4 功率的计算及公式的应用】
18.某科研所新研发了一款微型机器人,它可拖动比自身重大很多的物体。机器人质量是1.2×10﹣2kg,它静止在水平地面上时,与地面的接触面积是1×10﹣4m2。求:
(1)它受到的重力是多少?
(2)静止时,它对水平地面的压强是多少?
(3)若它用110N的水平拉力在10s内匀速拖动重物前进1m,则拉力的功率是多少?
19.2021年6月25日,西藏自治区首条电气化铁路拉林铁路开通运营,历史性地实现复兴号动车组对31个省区市的全覆盖,翻开了西藏和高原铁路建设发展新篇章。旦增乘坐某次列车从拉萨去林芝旅游,列车经过平直的藏木特大桥时,如图甲所示,他用手表测量了自己通过大桥的时间,上桥和离桥时的手表示数如图乙所示。通过查询资料得知列车功率约为5×106W,若列车过桥时速度保持25m/s不变。求:
(1)旦增过桥所用的时间;
(2)大桥的长度;
(3)列车过桥时所受阻力的大小。
20.一质量为5t的载重货车,现装有质量为25t的货物以20m/s的速度匀速行驶在水平公路上,汽车匀速行驶时,受到的阻力是总重的0.1倍(g取10N/kg),求:
(1)货车匀速行驶1h,牵引力做的功;
(2)若整个过程中货车的功率不变,货车上坡时的牵引力需增大为水平路面的2倍,求车上坡时的速度。
21.为助力乡村振兴,中山市某街道将生态农业和旅游观光相结合,打造美丽乡村。如图是该街道夏日乡村游用的观光艇,其部分技术参数如表:(g=10N/kg,ρ水=1.0×103kg/m3)
商品名称 浪花牌观光艇
商品型号 长7.5m×宽2.0m×深0.9m
空船质量 800kg
发动机最大输出功率 40kW
最大载人数量 8人
最大航速 10m/s
(1)若人的质量为50kg,当观光艇满载时,所受的浮力是多少?
(2)当观光艇以最大速度匀速航行时,受到水的平均阻力为多大?航行2km,发动机做功多少?
(3)小曾观察到艇身上标注的最大吃水线为50cm。当吃水达到该位置时,水对艇底部的压强是多大?
22.“海斗号”自主遥控水下机器人由中国科学院沈阳自动化研究所研发,最大潜深达10767米。海斗号成为我国首台下潜深度超过万米并进行科考应用的无人自主潜水器,海斗号总质量为35t,体积为60m3。(此前国内下潜深度最大的载人潜水器为蛟龙号,ρ海水≈1×103kg/m3,g=10N/kg)
(1)海斗号在我国首次万米深渊科考航次中,累计下潜七次,其中五次下潜是深度大于8000米的深渊科考应用,求第一次下潜到8000米时海斗号所受海水压强的大小。
(2)海斗号下潜到8000米后打开探照灯,摄像头通过观测孔了解8000米处深海的秘密,假设观测孔的面积为4dm2,求此时观测孔所受海水压力的大小。
(3)海斗号在完成某次任务后,匀速直线上升返回海面。若海斗号在水中以0.5m/s的速度匀速上浮,求浮力做功的功率和海斗号所受海水阻力大小。(设海斗号所受海水阻力大小不变)
23.如图所示,动滑轮重4N,所吊重物B重20N,物体A重240N,此时物体B恰好在20s内匀速下降了2m,不计绳重、绳子的伸长和滑轮组内部的摩擦。求:
(1)物体B下降的速度是多大?
(2)水平面对物体A的摩擦力是多大?
(3)要使物体B恰好以0.2m/s的速度匀速上升,则要对物体A施加水平向右拉力F的功率为多大?
【计算5 机械效率的计算】
24.图甲是某落锤式打桩机实物图,打桩机是利用冲击力将桩打入地层的桩工机械。其原理示意图如图乙所示。桩锤由卷扬机用吊钩提升,释放后自由下落而打桩。已知桩锤的质量为400kg,桩锤的底面积为0.1m2,桩顶的面积为0.04m2。求(g取10N/kg):
(1)若桩锤下落打在桩上的压力为4×105N,此时桩锤对桩的压强。
(2)若卷扬机把桩锤匀速提升2m,所用时间为2s,在此提升过程中打桩机的功率为8×103W。
①此过程中的有用功。
②此过程中打桩机的机械效率。
25.今年以来云南干旱少雨,为解决生活用水,扎西同学用一台功率为500W的抽水机将水从井中抽往12m高的楼顶水箱中,用时10min把容积为2m3的水箱装满。求:
(1)水箱中水的质量;
(2)抽水机抽水过程中对水做的有用功;
(3)抽水机抽水时的效率。
26.图1所示为工人师傅乘坐吊篮在高空粉刷楼体外墙的情景,吊篮可在电动机的作用下实现升降,其简化结构原理如图2所示。吊篮的质量为60kg,两名工人及工具的总质量为240kg,某次吊升过程中,吊篮在30s内匀速上升了6m。不计滑轮重、绳重和摩擦。
(1)电动机对绳子的拉力?
(2)电动机对吊篮(包括人及工具)做的功和功率?
(3)对吊篮做的功为额外功,对人和工具做的功为有用功,则机械效率是多少?
27.某型号挖掘机的实物图(甲)和作业范围图(乙)以及部分相关数据表,如图所示。挖掘机在4s内将装满铲斗的泥土从最大挖掘深度处送到位于最大卸料高度的装载车上。
项目 数值
满斗泥土的质量(kg) 600
A最大挖掘深度(m) 3
B最大卸料高度(m) 5
(1)移送泥土过程中,挖掘机对泥土做的功。
(2)移送泥土过程中,挖掘机的总功率为20kW,此过程中挖掘机的效率。
(3)挖掘机所做的额外功可将500N的物体抬高几米。
【计算6 滑轮(组)的机械效率】
28.如图所示,分别直接用力F1和使用滑轮用力F2,拉着高为h、底面积为S、质量为m的同一长方体金属块在同一水平路面上做匀速直线运动,移动L的距离。求:
(1)图中金属块静放在地面时对地面的压强;
(2)拉力在使用滑轮的过程中做的总功;
(3)该滑轮的机械效率。
29.如图所示,物体重180N,动滑轮重20N,绳重和轴摩擦不计。在竖直向上的拉力F的作用下,物体上升了4m。
(1)求绳子自由端移动的距离;
(2)求此过程中所做的额外功;
(3)求此过程中所做的有用功;
(4)求机械效率。
30.小南利用图甲的滑轮组,将一实心长方体以0.2m/s的速度匀速从水底拉出水面,图乙是该实心长方体所受拉力F1随时间t变化的图像。(不计摩擦、水的阻力及绳重)。求:
(1)实心长方体浸没时受到的浮力;
(2)实心长方体从水底到露出水面前,上升的高度;
(3)实心长方体从水底到露出水面前,若人对绳的拉力F2做功400J,求此过程中滑轮组的机械效率。
31.如图所示,工人借助滑轮组把重为350N的货物匀速提升了3m,已知绳子端拉力大小为200N,忽略摩擦及绳重。求:
(1)绳子自由端移动的距离和动滑轮的重。
(2)工人做的有用功。
(3)工人做的额外功。
(4)滑轮组的的机械效率。
32.如图甲所示,质量为40kg的小荣同学站在高台上竖直向上匀速拉动绳子,脚与地面的总接触面积为0.04m2,现改变G物,计算并绘出机械效率η与G物的关系图像如图乙所示,不计绳重和摩擦,求:
(1)动滑轮的重力G动;
(2)当G物=120N时,若此时人在10s内将物体提升了2m,则此时拉力的功率;
(3)若人站的位置能承受的最大压强为12500Pa,则该滑轮组所能提升物体的最大机械效率。
33.如图所示,某考古队用滑轮组将体积为100dm3的文物打捞出水,定滑轮重100N。滑轮组上共有三根绳子a、b和c,其中a是悬挂定滑轮,b绕在定滑轮和动滑轮上,c悬挂文物,整个打捞过程始终缓慢匀速提升文物,匀速提升文物0.5m(文物一直完全浸没在水中)时滑轮组所做的有用功为1.9×103J,滑轮组的机械效率为95%(g=10N/kg,绳重、滑轮与轴的摩擦以及水的阻力均忽略不计)。请解答下列问题:
(1)文物浸没在水中时受到的浮力是多大?
(2)动滑轮的重力是多大?
(3)在整个打捞过程中,a、b、c三根绳中哪根绳承受的拉力最大?该绳至少要承受多大的拉力?
【计算7 杠杆的机械效率】
34.用如图所示的杠杆从水平位置开始提升重物,用F=30N的动力始终竖直向上,将重为G=60N的物体缓慢提升0.1m,已知OA:OB=1:3,OA:OC=1:4,支点处的摩擦不计,求:
(1)杠杆自重G杆。
(2)杠杆提升重物的机械效率η。
(3)若将动力作用点从B点移到C点,其它条件不变,请说明杠杆的机械效率怎么变化?
35.如图所示,用竖直向上的拉力F作用在杠杆末端A点,将挂在杠杆中点B的重为150N的物体匀速缓慢提升0.5m。A点沿竖直方向上升1m。已知杠杆的质量分布均匀,自重为30N。(不计绳重及摩擦)
(1)求力F的大小;
(2)求将重物匀速提升时杠杆的机械效率(结果保留到0.1%)。
36.如图所示是一种小型千斤顶示意图,当手往下压动摇臂时,能把重物抬高一段较小的距离,工人在10s时间内用100N的力竖直向下压动摇臂2m,把1000N的重物匀速抬高14cm。
试求:
(1)工人做的功;
(2)此千斤顶的机械效率。
【计算8 斜面的机械效率】
37.如图,一辆货车匀速从山底A开到山顶B。货车重为5.0×104N,货车发动机的功率保持不变,山坡AB长2000m,高h为300m,牵引力保持2.5×104N不变,不计空气阻力。求:
(1)汽车从山底开到山顶所做的有用功。
(2)山坡的机械效率。
(3)汽车在山坡上行驶时的摩擦力。
38.如图所示,斜面长5m,高3m,物体A的重力为200N,物体B的重力280N,动滑轮的重力为20N。滑轮组绳子平行于斜面连接物体A,在滑轮组与物体B的作用下,能使物体A由斜面底端被匀速拉至顶端(不计绳重、滑轮与绳间的摩擦力、空气阻力)。
求:(1)绳子拉力F对物体A所做的有用功多少?
(2)该斜面的机械效率多少?
(3)物体A受到的滑动摩擦力多少?
39.如图所示,斜面长5m,小明用绳子沿与水平面成30度角的斜面将重为300N的木块由斜面底端匀速拉到顶端,拉力大小为240N,绳重不计。求:
(1)斜面对木块的摩擦力多大。
(2)斜面的机械效率。
40.如图所示,利用斜面将箱子推进车厢,通常要比把箱子直接从地面搬进车厢省力多了,某同学用150N的力沿斜面向上匀速推动箱子,已知箱子质量为30kg,斜面长3m,斜面高1.2m,g=10N/kg。求:
(1)箱子受到的重力;
(2)箱子受到的摩擦力;
(3)斜面的机械效率;
(4)使用斜面推箱子时有哪些更省力的方法。
参考答案
【计算1杠杆的平衡条件】
1.见试题解答内容
【分析】(1)知道正方体M的质量,根据G=mg求出正方体M的重力;
(2)根据杠杆平衡条件求出小萍离O点的距离;
(3)小萍站立在距离B端1.5m处时,根据杠杆的平衡条件求出A端细线的拉力,正方体M对水平地面的压力等于自身的重力减少绳子的拉力,受力面积等于正方体M的底面积,利用p=求出正方体M对水平地面的压强。
【解答】解:(1)由G=mg可得,正方体M的重力:
G木=m木g=40kg×10N/kg=400N;
(2)M对地面的压力刚好为0,则地面对M的支持力也为0,对M做受力分析,它受到竖直向下的重力和竖直向上的拉力,且拉力与重力相等,即F拉=G木=400N,
杠杆对重物M的拉力F拉与重物M对杠杆的拉力F1相等,即F1=F拉=400N;
设小萍离O点的距离为l2,由杠杆平衡条件F1l1=F2l2得F1 OA=G人l2,即:
l2==0.8m;
(3)小萍站立在距离B端L1=1.5m处时,由杠杆的平衡条件可得:
FA OA=G人 (AB﹣OA﹣L1),
即:FA×1m=500N×(3m﹣1m﹣1.5m),
解得:FA=250N,
正方体M对水平地面的压力:
F=GM﹣FA=400N﹣250N=150N,
正方体M对水平地面的压强:p==3.75×103Pa。
答:(1)正方体M的重力400N;
(2)当正方体M对地面压力刚好为0时,小萍距O点的距离0.8m;
(3)如果小萍站立在距离B端1.5m处时,正方体M对水平地面的压强为3.75×103Pa。
2.(1)被称物体的重力为100N;
(2)OB的长度是40cm。
【分析】杆秤是利用杠杆原理工作的,应用杠杆平衡条件分析解答。
(1)已知阻力与阻力臂、动力臂,由杠杆平衡条件可以求出动力,即物体的重力。
(2)已知阻力、阻力臂、动力,由杠杆平衡条件可以求出动力臂。
【解答】解:(1)由杠杆平衡条件得:G物体CO=G秤砣OD,
即:G物体×2cm=10N×20cm,
解得:G物体=100N;
(2)由杠杆平衡条件得:G最大CO=G秤砣OB,
即:200N×2cm=10N×OB,
解得:OB=40cm;
答:(1)被称物体的重力为100N;
(2)OB的长度是40cm。
3.(1)当阀门刚好被拉开时,蒸汽对阀门向上的压力为120N;
(2)当阀门刚好被拉开时,A点受到的压力大小为100N;
(3)B点所挂重物的重力大小为25N。
【分析】(1)根据已知条件,由压强公式得出蒸汽对阀门向上的压力;
(2)由已知条件,根据压强公式得出当阀门刚好被拉开时A点受到的压力大小;
(3)O为支点,当阀门刚好被拉开时,A点受到的压力大小为FA,根据杠杆的平衡条件得出B点所挂重物的重力。
【解答】解:(1)阀门的底面积为2cm2,锅炉内气体压强的安全值为6×105Pa,当阀门受到的蒸汽压力超过其安全值时,阀门就会被拉开,故当阀门刚好被拉开时,根据压强公式,蒸汽对阀门向上的压力
F=pS=6×105Pa×2×10﹣4m2=120N;
(2)锅炉外的大气压p0=1×105Pa,当阀门刚好被拉开时,A点受到的压力大小;
FA=ΔpS=(6×105Pa﹣1×105Pa)×2×10﹣4m2=100N;
(3)O为支点,当阀门刚好被拉开时,A点受到的压力大小为FA,
根据杠杆的平衡条件可知有FA OA=G OB
即100N 0.25m=G 1m
故B点所挂重物的重力:
G=25N。
答:(1)当阀门刚好被拉开时,蒸汽对阀门向上的压力为120N;
(2)当阀门刚好被拉开时,A点受到的压力大小为100N;
(3)B点所挂重物的重力大小为25N。
4.(1)M底部受到的水对它的压强为500Pa;
(2)M受到的水对它的浮力为5N;
(3)F的大小为18.75N。
【分析】(1)当M的一半体积浸在水中时,求出M的底部所处的深度,利用压强公式求M底部受到的水对它的压强;
(2)当M的一半体积浸在液体中时,根据排开水的体积,利用F浮=ρ液V排g求出M受到的水对它的浮力;
(3)根据受力平衡求出M对B点的拉力,利用杠杆平衡条件计算拉力F。
【解答】解:(1)当M的一半体积浸在水中时,M的底部所处的深度:h=L=×10cm=5cm=0.05m,
M底部受到的水对它的压强:p=ρ水gh=1.0×103kg/m3×10N/kg×0.05m=500Pa;
(2)当M的一半体积浸在液体中时,排开水的体积:V排=L3=×(10cm)3=500cm3=5×10﹣4m3,
则此时M受到的水对它的浮力:F浮=ρ水V排g=1.0×103kg/m3×10N/kg×5×10﹣4m3=5N;
(3)M对B点的拉力:FB=G﹣F浮=20N﹣5N=15N,
由杠杆平衡条件可得:FB×OB=F×OA,
则:F===18.75N。
答:(1)M底部受到的水对它的压强为500Pa;
(2)M受到的水对它的浮力为5N;
(3)F的大小为18.75N。
5.(1)当轻质杠杆在水平位置平衡时,细绳对圆台体材料的拉力为2N;
(2)当轻质杠杆在水平位置平衡时,圆台体材料受到的浮力为10N;
(3)圆台体材料的密度为1.2×103kg/m3。
【分析】(1)设绳子对圆台体建筑材料的拉力为F2,则绳子对杠杆的拉力F1=F2,根据杠杆平衡条件可求出绳子对杠杆的拉力F1;
(2)圆台体建筑材料静止在水中,处于平衡状态,根据G=F浮十F2可求出材料浸没在水中静止时受到的浮力;
(3)根据阿基米德原理可求出圆台体的体积,从而求出其密度。
【解答】解:(1)设绳子对圆台体建筑材料的拉力为F2,
绳子对杠杆的拉力F1=F2,
根据杠杆的平衡条件可知:Fl1=F1l2,
即:0.5N×0.4m=F1×0.1m,得出F1=2N,
则细绳对圆台体材料的拉力F2=F1=2N;
(2)圆台体建筑材料静止在水中,处于平衡状态,则:
G=F浮十F2,
材料浸没在水中静止时受到的浮力为:
F浮=G﹣F2=12N﹣2N=10N;
(3)由F浮=G排=ρ水gV排可知,物体的体积为:
V=V排===10﹣3m3,
材料的密度为:ρ材料====1.2×103kg/m3。
答:(1)当轻质杠杆在水平位置平衡时,细绳对圆台体材料的拉力为2N;
(2)当轻质杠杆在水平位置平衡时,圆台体材料受到的浮力为10N;
(3)圆台体材料的密度为1.2×103kg/m3。
6.(1)A的质量为0.6kg;
(2)C对水平地面的压强为6000Pa;
(3)液体的质量为3.1kg。
【分析】(1)由图乙中图表可知,注入水后所受的浮力先增加,然后不变,最后再增大,说明图形中水平的位置就是物体漂浮的过程,由图表可知A受到的浮力,再利用浮沉条件此时F浮=GA可求出A的重力,再用m=可得出A的质量;
(2)由杠杆平衡条件可计算出C所受的拉力,再根据受力分析可以求出所受到的支持力,由于支持力和压力是一对相互作用力,可以求出C对地面的压力,再利用p=可以求出C对地面的压强;
(3)题目已知C的地面的压强,用F=pS可以计算出C对地面的压力,从而得出C所受到的压力,再根据受力分析,可得出C所受的拉力大小,利用杠杆平衡的条件和受力分析,可得出B此时所受到的浮力。
【解答】解:(1)由图象知,当h水深为6﹣13cm时,浮力不变,且小于A的边长,说明没有浸没,故此时物体A漂浮,
再利用浮沉条件此时F浮=GA,所以GA=6N;
所以物体A的重力为6N;
A的质量为m===0.6kg;
(2)当未注入水时,物体B所受到的重力GB=mg=1kg×10N/kg=10N,
利用杠杆平衡条件可知,GBOM=F拉CON,
由于OM:ON=4:1,所以此时C所受到的拉力F拉C=40N,
C所受到支持力F支=GC﹣F拉C=100N﹣40N=60N,
由于压力和支持力互为相互作用力,F压=F支=60N,
由p=可得,C对地面的压强为p===6000Pa;
C对水平地面的压强为6000Pa;
(3)由F=ps可得,此时C对水平地面的压力为F=pS=8800Pa×100cm2=88N;
由于压力和支持力互为相互作用力,C所受到支持力F支′=F压′=88N,
C所受到拉力F拉C′=GC﹣F支′=100N﹣88N=12N,
利用杠杆平衡条件可知,F拉BOM=F拉C′ON,
由于OM:ON=4:1,所以此时B所受到的拉力F拉B=3N,
假设此时A未浸没,
B所受到A的作用力为FA对B=GB﹣F拉B=10N﹣3N=7N,
此时A所受到的浮力为F浮A=GA+FB对A=6N+7N=13N,
而A全浸没所受到的浮力F浮全=ρ液gV排=1×103kg/m3×1000×10﹣6m3×10N/kg=10N,
与假设的条件不符,所以A应该已经全浸没,
那么A所受到B对A的作用力FB对A=F浮全﹣GA=10N﹣6N=4N,
B所受到A对B的作用力FA对B=4N,
B受到的浮力为F浮B=GB﹣FA对B﹣F拉B=10N﹣4N﹣3N=3N,
由F浮=ρ水V排g可得浮体排开水的体积:
V排B=3×10﹣4m3=300cm3,
B浸入深度为:h浸B==5cm,
由图表可知A漂浮且AB之间接触而无作用力的水深为13cm,
由F浮=ρ水V排g可得A排开水的体积:
V排A=6×10﹣4m3=600cm3,
h浸A==6cm,
所以此时水面的深度为:
h水=h浸B+(LA﹣h浸A)+13cm=5cm+(10cm﹣6cm)+13cm=22cm,
那么此时加入的V液=V总﹣V排A﹣V排B=22cm×200cm2﹣1000cm3﹣300 cm3=3100cm3,
液体的质量m液=ρ液V液=1×103kg/m3×3300×10﹣6m3=3.1kg;
答:(1)A的质量为0.6kg;
(2)C对水平地面的压强为6000Pa;
(3)液体的质量为3.1kg。
【计算2 滑轮组中的相关计算】
7.(1)物体在水平面上受到的滑动摩擦力是10N;
(2)拉力F的大小是4N;
(3)拉力F在10秒内移动的距离是3m。
【分析】(1)根据G=mg得出物体的重力,根据f=0.1G得出物体在水平面上受到的滑动摩擦力;
(2)物体匀速运动,处于平衡状态,根据F物=f得出滑轮组对物体的拉力,
从图中可知n=3,不计绳重和绳与滑轮间的摩擦力,根据F=(G动+F物)得出拉力F;
(3)根据s=vt得出物体在10s内移动的距离s,根据s′=ns得出拉力F在10秒内移动的距离。
【解答】解:(1)物体的重力G=mg=10kg×10N/kg=100N,
物体在水平面上受到的滑动摩擦力f=0.1G=0.1×100N=10N;
(2)物体匀速运动,处于平衡状态,滑轮组对物体的拉力F物=f=10N,
从图中可知n=3,不计绳重和绳与滑轮间的摩擦力,拉力F=(G动+F物)=×(2N+10N)=4N;
(3)物体在10s内移动的距离s=vt=0.1m/s×10s=1m,
拉力F在10秒内移动的距离s′=ns=3×1m=3m。
答:(1)物体在水平面上受到的滑动摩擦力是10N;
(2)拉力F的大小是4N;
(3)拉力F在10秒内移动的距离是3m。
8.(1)物体的重力为400N;
(2)工人所施加的拉力大小为200N;
(3)该工人用此装置不能拉起重为1400N的物体。
【分析】(1)根据G=mg求出物体的重力;
(2)根据滑轮组装置确定绳子股数,忽略绳重、摩擦和动滑轮重力,利用F=G求出工人所施加的拉力大小;
(3)根据G=mg求出人的重力,绳子自由端受到最大拉力为人的重力,即F'=G人,利用F'=G'求出工人能拉起的最大物重。
【解答】解:(1)箱子的质量为40kg,故箱子的重力为G=mg=40kg×10N/kg=400N;
(2)由图可知,n=2,忽略绳重、摩擦和动滑轮重力,工人所施加的拉力大小为:
F=G=×400N=200N;
(3)工人的质量为60kg,故工人的重力为G人=m人g=60kg×10N/kg=600N,绳子自由端受到最大拉力为人的重力,即F'=G人=600N,
根据F'=G'可知,工人能拉起的最大物重为:
G'=nF'=2×600N=1200N<1400N,
故该工人用此装置不能拉起重为1400N的物体。
答:(1)物体的重力为400N;
(2)工人所施加的拉力大小为200N;
(3)该工人用此装置不能拉起重为1400N的物体。
9.(1)所提物体的重力为200N;
(2)作用在绳子自由端的拉力为110N;
(3)绳子自由端的移动速度为0.4m/s。
【分析】(1)知道物体的质量,根据G=mg计算出重力;
(2)由图可知n=2,不计绳重和摩擦,根据F=算出绳子自由端的拉力;
(3)根据s=nh算出绳子自由端移动的距离,再利用v=计算出绳子自由端的移动速度。
【解答】解:(1)质量为20kg的物体的重力为
G=mg=20kg×10N/kg=200N;
(2)不计绳重和摩擦,如图,滑轮组的动滑轮和重物由2条绳子共同对它们施加了向上的拉力,因为定滑轮不省力只能改变力的方向,所以绳子自由端的拉力即为重物和动滑轮总重力的一半:
F===110N;
(3)因为n=2,所以绳子自由端移动的距离是物体上升高度的2倍,物体向上移动了2m,所以绳子自由端移动的距离是4m,则绳子自由端的移动速度为
v===0.4m/s。
答:(1)所提物体的重力为200N;
(2)作用在绳子自由端的拉力为110N;
(3)绳子自由端的移动速度为0.4m/s。
10.(1)人收绳的速度为2m/s;
(2)人的拉力为310N;
(3)压强为2400Pa。
【分析】(1)利用速度计算公式求得物体上升的速度,再利用v=nv物求得人收绳的速度;
(2)根据G=mg计算重力,根据图中知,绳子的股数n=2,不计绳重及滑轮摩擦,根据公式F=(G+G动)求出拉力;
(2)根据F=G计算压力,根据p=计算压强。
【解答】解:(1)由题意可得,动滑轮上有两股绳,物体上升的速度为=1m/s,
则人收绳子的速度为v=2v物=2×1m/s=2m/s;
(2)由重力计算公式可得G物=mg=60kg×10N/kg=600N,
不考虑绳子与轮的摩擦,人的拉力为F=(G+G动)=×(600N+20N)=310N;
(3)由题意可得,水泥板放地面时的受力面积为S=50×10﹣2m×50×10﹣2m=0.25m2,
由压强公式可得p==2400Pa。
答:(1)人收绳的速度为2m/s;
(2)人的拉力为310N;
(3)压强为2400Pa。
11.(1)A浸没在水中所受浮力为400N;
(2)A露出水面前,绳子自由端的拉力为125N;
(3)人对地面的压强为6×103Pa。
【分析】(1)根据F浮=ρ液gV排求出A浸没在水中所受浮力;
(2)根据G=mg求出A的重力,根据力的平衡条件求出A浸没在水中时受到的拉力,
由图可知n=2,利用不计绳重和摩擦时F=(F拉+G动)求出绳子自由端的拉力;
(3)物体A出水后,根据F′=(G+G动)求出人对绳子自由端的拉力,此时人对水平地面的压力等于人的重力减去绳子自由端的拉力,根据p=求人对地面的压强。
【解答】解:(1)因为A浸没在水中,所以A排开水的体积:
V排=V=0.04m3,
则A所受的浮力:
F浮=ρ水gV排=1×103kg/m3×10N/kg×0.04m3=400N;
(2)A的重力:
G=mg=60kg×10N/kg=600N,
由力的平衡条件可知,A浸没在水中时受到的拉力:
F拉=G﹣F浮=600N﹣400N=200N,
由图可知n=2,因为不计绳重和摩擦及水的阻力,所以A露出水面前,绳子自由端的拉力:
F=(F拉+G动)=×(200N+50N)=125N;
(3)物体A出水后,人对绳子自由端的拉力:
F′=(G+G动)=×(600N+50N)=325N,
人对水平地面的压力:
F压=G人﹣F′=625N﹣325N=300N,
人对地面的压强:
p===6×103Pa。
答:(1)A浸没在水中所受浮力为400N;
(2)A露出水面前,绳子自由端的拉力为125N;
(3)人对地面的压强为6×103Pa。
【计算3 功的计算和公式的应用】
12.(1)行驶这段路程所用的时间为0.5h;
(2)电动汽车在水平公路匀速行驶时牵引力为560N;
(3)电动汽车匀速行驶60km,牵引力所做的功为3.36×107J。
【分析】(1)已知电动车行驶的路程和速度,根据v=计算行驶这段路程所用的时间;
(2)电动汽车对地面的压力等于汽车和人的总重力,根据G=mg求出总重力;然后求出阻力;由于汽车匀速行驶,汽车受到的牵引力、阻力是一对平衡力,大小相等,据此求出牵引力;
(3)根据W=Fs便可计算出牵引力做的功。
【解答】解:(1)由v=可得,行驶这段路程所用的时间:
t==0.5h;
(2)电动汽车匀速行驶时的总重力为:
G=(m1+m2)g=(1340kg+60kg)×10N/kg=1.4×104N;
电动汽车匀速行驶,所以牵引力与阻力平衡,
则电动汽车受到的牵引力为:
F=f=0.04G=0.04×1.4×104N=560N;
(3)则电动车行驶60km,牵引力做的功为:
W=Fs=560N×60×103m=3.36×107J;
答:(1)行驶这段路程所用的时间为0.5h;
(2)电动汽车在水平公路匀速行驶时牵引力为560N;
(3)电动汽车匀速行驶60km,牵引力所做的功为3.36×107J。
13.(1)小伟热身运动的平均速度为2m/s;
(2)小伟的体重是500N;
(3)小伟完成1次引体向上克服重力做的功为300J;
(4)小伟双脚站在水平地面上时对地面的压强约为1×104Pa。
【分析】(1)知道小伟跑的路程和时间,根据v=求出其平均速度;
(2)利用G=mg计算小伟的体重;
(3)利用W=Gh求出完成1次引体向上做的功;
(4)小伟双脚站在水平地面上对地面的压力等于其重力,根据p=求出他对地面的压强。
【解答】解:(1)小伟热身运动的平均速度为:
v===2m/s;
(2)小伟的体重为:
G=mg=50kg×10N/kg=500N,
(3)完成1次引体向上做的功为:
W=Gh=500N×0.6m=300J;
(4)小伟双脚站在水平地面上对地面的压力为:
F=G=500N,
双脚与地面的接触面积约为:
S=2×250cm2=500cm2=500×10﹣4m2,
则对地面的压强:
p===1×104Pa。
答:(1)小伟热身运动的平均速度为2m/s;
(2)小伟的体重是500N;
(3)小伟完成1次引体向上克服重力做的功为300J;
(4)小伟双脚站在水平地面上时对地面的压强约为1×104Pa。
14.(1)货车停下后对地面的压强为5×106Pa;
(2)货车匀速行驶10s牵引力做的功为6×106J。
【分析】(1)知道载重货车的总质量,利用重力的计算公式G=mg可以计算出其受到的总重力;载重货车对地面的压力等于其总重力,知道受力面积,利用公式p=求货车对地面的压强;
(2)由v=得车匀速行驶10s行驶的路程,根据阻力与重力的关系求出阻力,再根据二力平衡的条件求出牵引力的大小,利用W=Fs求得牵引力做的功。
【解答】解:(1)车的总质量:m总=5t+25t=30t=30000kg,
车受到的总重力:G=mg=30000kg×10N/kg=3×105N,
汽车对地面的压强p===5×106Pa;
(2)车匀速行驶10s行驶的路程s=vt=20m/s×10s=200m,
由二力平衡条件可得,汽车的牵引力F牵引力=f=0.1G=0.1×3×105N=30000N,
汽车牵引力所做的功W=F牵引力s=30000N×200m=6×106J。
答:(1)货车停下后对地面的压强为5×106Pa;
(2)货车匀速行驶10s牵引力做的功为6×106J。
15.1)空鱼缸对窗台的压强为500Pa;
(2)注水后鱼缸底部受到水的压强为1000Pa;
(3)抬高鱼缸的过程中,小明对鱼缸和水总共做的功为6J。
【分析】(1)知道鱼缸的重力;因为在水平桌面上,利用F=G求鱼缸对桌面的压力,再利用p=求鱼缸对桌面的压强;
(2)知道鱼缸内水深和水的密度,利用液体压强公式求水对鱼缸底的压强;
(3)求出鱼缸和水的总重力,根据W=Fs=Gh求出小明对鱼缸和水总共做的功。
【解答】解:(1)空鱼缸对桌面的压力:F=G=5N,
空鱼缸对窗台的压强:
p===500Pa;
(2)注水后鱼缸底部受到水的压强:
p′=ρgh=1×103kg/m3×10N/kg×10×10﹣2m=1000Pa;
(3)水和鱼缸的总重力:
G总=G+G水=G+m水g=5N+1.5kg×10N/kg=20N,
抬高鱼缸的过程中,小明对鱼缸和水总共做的功:
W=Fs=G总h=20N×0.3m=6J,
答:(1)空鱼缸对窗台的压强为500Pa;
(2)注水后鱼缸底部受到水的压强为1000Pa;
(3)抬高鱼缸的过程中,小明对鱼缸和水总共做的功为6J。
16.(1)注水过程中,“背漂”受到的最大浮力为30N。
(2)细线的长度15cm。
(3)注水过程中,浮力对“背漂”所做的功为0.225J。
【分析】(1)由图像知当“背漂”完全浸没时的拉力,此时受到的浮力最大,根据F浮最大=F+G算出最大浮力;
(2)“背漂”刚好漂浮时,浮力等于重力,计算水的深度,根据绳子刚开始有拉力的深度,计算物体上升的高度,即绳子的长度;
(3)根据细线的长度,即“背漂”上升的高度,然后根据功的计算公式求出“背漂”做的功。
【解答】解:(1)由图像知当“背漂”完全浸没时,拉力F=28.5N,受到的浮力最大,最大浮力为:
F浮最大=F+G=28.5N+1.5N=30N;
(2)“背漂”刚浮起来时,受到的浮力为:
F浮=G=1.5N,此时水的深度等于“背漂”浸没水中的深度,由F浮=ρ液gV排知“背漂”排开水的体积为:
V排===1.5×10﹣4m3=150cm3,
此时容器中水的深度为:
h===0.4cm;
当绳子刚好有拉力时,水的深度为15.4cm,则绳子的长度为15.4cm﹣0.4cm=15cm。
(3)细线的长度为L=15cm=0.15m,即在浮力作用下“背漂”向上移动的距离为s=L=0.15m,所以浮力对“背漂”做的功为:
W=F浮L=1.5N×0.15m=0.225 J。
答:(1)注水过程中,“背漂”受到的最大浮力为30N。
(2)细线的长度15cm。
(3)注水过程中,浮力对“背漂”所做的功为0.225J。
17.(1)物块的重力为30N;
(2)在2~4s内物块运动的平均速度为1m/s;
(3)在前6s内,拉力F做的功为42J。
【分析】(1)根据G=mg可求出物块的重力;
(2)在速度—时间图像中,物体运动的距离等于这段时间的图像与t轴之间的面积;由图丙求出在2~4s内物块运动的距离,根据v=求出其平均速度;
(3)根据图丙得出在0~2s内物块处于静止状态,从而得出拉力不做功;根据题意可知物块在2~4s的运动距离,根据W=Fs求出拉力F做的功;利用v=求出物块在4~6s内运动的距离,根据W=Fs求出拉力F做的功;然后求出前6s内拉力F做的功。
【解答】解:(1)物块的重力为G=mg=3kg×10N/k=30N;
(2)由图丙知,在2~4s内物块运动的距离等于这段时间的图像与t轴之间的面积,即s==2m,其平均速度v=;
(3)由图丙可知,在0~2s内,物块的速度为0处于静止状态,拉力不做功,W1=0;
由(2)可知,物块在2~4s的运动距离为s=2m,拉力F做的功W2=F2s=9N×2m=18J;
由图丙可知,物块在4~6s内以2m/s的速度做匀速直线运动,由v=可得,物块在4~6s内运动的距离s3=v3t3=2m/s×(6s﹣4s)=4m,
由图乙可知,物块在4~6s内受到的拉力为6N,
拉力F做的功W3=F3s3=6N×4m=24J;
所以,前6s内拉力F做的功W总=W1+W2+W3=0J+18J+24J=42J。
答:(1)物块的重力为30N;
(2)在2~4s内物块运动的平均速度为1m/s;
(3)在前6s内,拉力F做的功为42J。
【计算4 功率的计算及公式的应用】
18.(1)机器人受到的重力是0.12N;
(2)静止时,它对水平地面的压强是1200Pa;
(3)拉力的功率是11W。
【分析】(1)知道机器人的质量,利用重力公式求其重力;
(2)机器人对水平地面的压力等于重力,又知道受力面积,利用压强公式求机器人对地面的压强;
(3)由W=Fs计算拉力做的功,由P=计算拉力的功率。
【解答】解:拉力的功率
(1)微型机器人的重力:
G=mg=1.2×10﹣2kg×10N/kg=0.12N;
(2)机器人静止时,它对水平地面的压力F=G=0.12N,
对水平地面的压强:
p===1200Pa;
(3)拉力做的功:
W=Fs=110N×1m=110J,
拉力的功率:
P===11W。
答:(1)机器人受到的重力是0.12N;
(2)静止时,它对水平地面的压强是1200Pa;
(3)拉力的功率是11W。
19.(1)旦增过桥所用的时间为21s;
(2)大桥的长度为525m;
(3)列车过桥时所受阻力的大小为2×105N。
【分析】(1)根据图乙中的信息可求出旦增过桥所用的时间;
(2)已知列车过桥时速度和所用的时间,根据s=vt求出列车通过的路程,即为大桥的长度;
(3)根据P===Fv求出列车受到的牵引力,利用二力平衡条件求出列车过桥时所受阻力的大小。
【解答】解:(1)由图乙可知,旦增过桥所用的时间为t=9:35:41﹣9:35:20=21s;
(2)列车过桥时速度保持25m/s不变,则大桥的长度为:
s=vt=25m/s×21s=525m;
(3)列车功率约为5×106W,列车过桥时速度保持25m/s不变,
则根据P===Fv可知,列车受到的牵引力为:
F===2×105N,
因列车过桥时速度不变,且藏木特大桥平直,即列车过桥时做匀速直线运动,所以列车过桥时所受阻力与牵引力为一对平衡力,
由二力平衡条件可得,列车过桥时所受阻力为:f=F=2×105N。
答:(1)旦增过桥所用的时间为21s;
(2)大桥的长度为525m;
(3)列车过桥时所受阻力的大小为2×105N。
20.(1)货车匀速行驶1h,牵引力做的功是2.16×109J;
(2)车上坡时的速度是10m/s。
【分析】(1)由求出货车匀速行驶1h通过的路程,根据重力公式求出载重货车的总重力,根据阻力与总重力的关系求出阻力,再根据二力平衡的条件求出牵引力的大小,再利用W=Fs求得牵引力做的功;
(2)整个过程中货车的功率不变,货车上坡时的牵引力需增大为水平路面的2倍,利用公式P=Fv求出车上坡时的速度。
【解答】解:(1)货车匀速行驶1h通过的路程:s=vt=20m/s×3600s=7.2×104m,
载重货车的总重力:G总=m总g=(m车+m货)g=(5+25)×103kg×10N/kg=3×105N,
由二力平衡条件可得,汽车的牵引力:F牵=f=0.1G总=0.1×3×105N=3×104N,
汽车牵引力所做的功:W=F牵s=3×104N×7.2×104m=2.16×109J;
(2)因为,行驶过程中货车的功率始终保持不变,所以P1=P2,则有F1v1=F2v2,
货车上坡时的牵引力增大为水平路面时的2倍(即F2=2F1),则车上坡时的速度:
。
答:(1)货车匀速行驶1h,牵引力做的功是2.16×109J;
(2)车上坡时的速度是10m/s。
21.(1)观光艇满载时,所受浮力是1.2×104N;
(2)观光艇以最大速度航行时,受到水的平均阻力是4×103N;航行2km,发动机做功8×106J;
(3)水对艇底部的压强为5×103Pa。
【分析】(1)从技术参数表得出观光艇和8人总质量,利用重力公式求人、观光艇总重力,再利用漂浮条件求观光艇满载时,所受水的浮力;
(2)从技术参数表得出发动机的最大功率,利用P===Fv的变形公式F=求牵引力;又因为观光艇匀速行驶,受平衡力,据此求受到水的平均阻力;由W=Fs可知发动机做功多少;
(3)利用p=ρgh求得水对艇底部的压强。
【解答】解:(1)观光艇满载时观光艇和8人总质量为:
m=800kg+50kg×8=1200kg,
满载时人、观光艇总重力为:
G=mg=1200kg×10N/kg=1.2×104N,
观光艇漂浮,观光艇满载乘客时所受浮力为:F浮=G=1.2×104N;
(2)P===Fv,则观光艇受到的牵引力为:
F===4×103N,
观光艇匀速行驶,故观光艇受到的牵引力和水的阻力为平衡力,
观光艇受到水的平均阻力为:
f=F=4×103N;
航行2km,发动机做功:W=Fs=4×103N×2×103m=8×106J;
(3)由p=ρ水gh可知当吃水达到该位置时,水对艇底部的压强为:
p=ρ水gh=1.0×103kg/m3×10N/kg×50×10﹣2m=5×103Pa。
答:(1)观光艇满载时,所受浮力是1.2×104N;
(2)观光艇以最大速度航行时,受到水的平均阻力是4×103N;航行2km,发动机做功8×106J;
(3)水对艇底部的压强为5×103Pa。
22.(1)第一次下潜到8000米时海斗号所受海水的压强为8×107Pa;
(2)此时观测孔所受海水的压力为3.2×106N;
(3)浮力做功的功率为3×105W,海斗号所受海水的阻力为2.5×105N。
【分析】(1)根据p=ρ液gh求出第一次下潜到8000米时海斗号所受海水的压强;
(2)知道海斗号下潜到8000米后所受海水的压强和观测孔的面积,根据F=pS求出此时观测孔所受海水的压力;
(3)海斗号匀速直线上升返回海面时排开海水的体积和自身的体积相等,根据F浮=ρ液gV排求出海斗号所受的浮力,利用P===Fv求出浮力做功的功率;对海斗号进行受力分析,根据海斗号受到的合力为零得出等式即可求出海斗号所受海水的阻力。
【解答】解:(1)第一次下潜到8000米时海斗号所受海水的压强:p=ρ海水gh=1×103kg/m3×10N/kg×8000m=8×107Pa;
(2)观测孔的面积:S=4dm2=4×10﹣2m2,
由p=可得,此时观测孔所受海水的压力:F=pS=8×107Pa×4×10﹣2m2=3.2×106N;
(3)因物体浸没时排开液体的体积和自身的体积相等,
所以,海斗号所受的浮力:F浮=ρ海水gV排=ρ海水gV=1×103kg/m3×10N/kg×60m3=6×105N,
浮力做功的功率:P===F浮v=6×105N×0.5m/s=3×105W;
因海斗号匀速直线上升返回海面时,受到竖直向上的浮力和竖直向下的重力、阻力作用处于平衡状态,
由海斗号受到的合力为零可得:F浮=G+f=mg+f,
则海斗号所受海水的阻力:f=F浮﹣mg=6×105N﹣35×103kg×10N/kg=2.5×105N。
答:(1)第一次下潜到8000米时海斗号所受海水的压强为8×107Pa;
(2)此时观测孔所受海水的压力为3.2×106N;
(3)浮力做功的功率为3×105W,海斗号所受海水的阻力为2.5×105N。
23.(1)物体B下降的速度是0.1m/s;
(2)水平面对物体A的摩擦力是12N;
(3)要使物体B恰好以0.2m/s的速度匀速上升,则要对物体A施加水平向右拉力F的功率为9.6W。
【分析】(1)根据v=算出物体B下降的速度;
(2)由图知,有2段绳子承担物重,即n=2,不计绳重、绳子的伸长和滑轮组内部的摩擦,当物体B匀速下降时,物体A受到水平向右滑动摩擦力的大小f=F拉=(GB+G动);
(3)当物体B匀速上升时,处于平衡状态,受平衡力的作用,对物体A施加水平向右的拉力等于向左的摩擦力加上滑轮组绳子自由端拉力,由于有2段绳子承担物重,所以物体A向右运动的速度等于物体B上升速度的2倍,利用P===Fv求拉力F的功率。
【解答】解:
(1)物体B下降的速度为:
vB===0.1m/s;
(2)由图知,有2段绳子承担物重,即n=2,不计绳重、绳子的伸长和滑轮组内部的摩擦,当物体B匀速下降时,物体A受到水平向右滑动摩擦力的大小为:
f=F拉=(GB+G动)=×(20N+4N)=12N;
(3)当物体B匀速上升时,绳子的拉力F拉不变,由于物体A受到的压力和接触面的粗糙程度不变,所以物体A受到的摩擦力大小不变,仍为12N,
由力的平衡条件可得,对物体A施加水平向右的拉力:
F=f+F拉=12N+12N=24N,
物体A向右运动的速度:
vA=2vB′=2×0.2m/s=0.4m/s,
拉力F的功率:
P===FvA=24N×0.4m/s=9.6W。
答:(1)物体B下降的速度是0.1m/s;
(2)水平面对物体A的摩擦力是12N;
(3)要使物体B恰好以0.2m/s的速度匀速上升,则要对物体A施加水平向右拉力F的功率为9.6W。
【计算5 机械效率的计算】
24.(1)桩锤对桩的压强是1×107Pa;
(2)①此过程中的有用功为8×103J;
②此过程中打桩机的机械效率为50%。
【分析】(1)已知压力和受力面积,根据压强公式P=,可求出桩锤对桩的压强;
(2)利用W有=Gh=mgh求出卷扬机克服重力做的功;
利用W总=Pt求出总功,根据效率公式η=×100%可求出卷扬机的效率。
【解答】解:(1)桩锤对桩的压强是:
P===1×107Pa;
(2)①卷扬机克服重力做的有用功是:
W有=Gh=mgh=400kg×10N/kg×2m=8×103J;
②卷扬机做的总功是:
W总=Pt=8×103W×2s=1.6×104J,
卷扬机的效率是:
η=×100%=×100%=50%。
答:(1)桩锤对桩的压强是1×107Pa;
(2)①此过程中的有用功为8×103J;
②此过程中打桩机的机械效率为50%。
25.(1)水箱中水的质量是2×103kg;
(2)抽水机抽水过程中对水做的有用功2.4×105J;
(3)抽水机抽水时的效率是80%。
【分析】(1)已知水的密度与水箱的容积,由密度公式求出水的质量;
(2)根据重力公式求出水的重力,再根据W=Gh求出抽水机所做的功;
(3)根据机械效率公式抽水机的效率。
【解答】解:(1)根据ρ=可得水箱中水的质量:
m=ρV=1.0×103kg/m3×2m3=2×103kg;
(2)水的重力:G=mg=2×103kg×10N/kg=2×104N,
抽水机抽水过程中对水做的有用功:
W有用=Gh=2×104N×12m=2.4×105J;
(3)抽水机抽水时的效率:
η==×100%=×100%=80%。
答:(1)水箱中水的质量是2×103kg;
(2)抽水机抽水过程中对水做的有用功2.4×105J;
(3)抽水机抽水时的效率是80%。
26.(1)电动机对绳子的拉力为750N;
(2)电动机对吊篮(包括人及工具)做的功为1.8×104J,功率为600W;
(3)对吊篮做的功为额外功,对人和工具做的功为有用功,则机械效率是80%。
【分析】(1)不计滑轮重、绳重和摩擦,根据F=G总求出电动机对绳子的拉力;
(2)求出绳子自由端移动的距离s=nh,根据W=Fs求出电动机对吊篮(包括人及工具)做的功,即总功;根据P=求出电动机对吊篮(包括人及工具)做功的功率;
(3)根据=Gh求出有用功,根据η=求出机械效率。
【解答】解:(1)由题图可知,绳子承重股数为n=4,不计滑轮重、绳重和摩擦,电动机对绳子的拉力为:F=G总=m总g=×(60kg+240kg)×10N/kg=750N;
(2)绳子自由端移动的距离为:s=nh=4×6m=24m,
电动机对吊篮(包括人及工具)做的功,即总功为:W总=Fs=750N×24m=1.8×104J;
电动机对吊篮(包括人及工具)做功的功率为:P==600W;
(3)有用功为:W有=Gh=mgh=240N×10N/kg×6m=1.44×104J;
机械效率为:η==80%。
答:(1)电动机对绳子的拉力为750N;
(2)电动机对吊篮(包括人及工具)做的功为1.8×104J,功率为600W;
(3)对吊篮做的功为额外功,对人和工具做的功为有用功,则机械效率是80%。
27.(1)移送泥土的过程中,挖掘机对泥土所做的功为4.8×104J;
(2)挖掘机的机械效率为60%;
(3)挖掘机所做的额外功可将500N的物体抬高64米。
【分析】(1)移送泥土的过程中,挖掘机对泥土所做的功,是指对泥土的重力做功,那么在重力的方向上移动的距离是最大挖掘深度和最大卸料高度之和,然后利用W=Gh即可求出挖掘机对泥土所做的功;
(2)先根据发动机的总功率是20kW求出挖掘机在4s内做的总功,再利用η=×100%.即可求出此过程挖掘机的机械效率;
(3)先计算出额外功,利用W=Gh计算将泥土提高的高度。
【解答】解:(1)满斗泥土所受重力:G=mg=600kg×10N/kg=6000N,
对泥土做功:W有=G泥h=6000N×(3m+5m)=4.8×104J;
(2)由P=得,挖掘机的发动机4s内做的总功:W总=Pt=2×104W×4s=8×104J;
挖掘机的机械效率:η=×100%=×100%=60%;
(3)挖掘机所做额外功:W额=W总﹣W有=8×104J﹣4.8×104J=3.2×104J,
由W=Gh得,可将500N的物体抬高高度:h′===64m。
答:(1)移送泥土的过程中,挖掘机对泥土所做的功为4.8×104J;
(2)挖掘机的机械效率为60%;
(3)挖掘机所做的额外功可将500N的物体抬高64米。
【计算6 滑轮(组)的机械效率】
28.(1)图中金属块静放在地面时对地面的压强为;
(2)拉力在使用滑轮的过程中做的总功为2F2L;
(3)该滑轮的机械效率为。
【分析】(1)金属块静止放在水平路面上时对地面的压力和自身的重力相等,利用p=求出金属块静放地面时对地面的压强;
(2)动滑轮绳子的有效股数为2,根据s=nL求出绳端移动的距离,利用W=Fs求出拉力做的总功;
(3)两种方式拉金属块时,金属块受到地面的摩擦力不变,用滑轮拉的过程中所做的有用功就是克服地面给金属块摩擦力所做的功,根据二力平衡条件求出受到的摩擦力,利用W=fL求出拉力在使用滑轮的过程中做的有用功;动滑轮的机械效率等于有用功题意总功之比。
【解答】解:(1)金属块静放在水平路面上时对地面的压力:F=G=mg,
金属块对地面的压强p==;
(2)动滑轮绳子的有效股数n=2,则绳端移动的距离s=nL=2L,
拉力做的总功W总=F2s=F2×2L=2F2L;
(3)因两种方式拉金属块时,金属块受到地面的摩擦力不变,用滑轮拉的过程中所做的有用功就是克服地面给金属块摩擦力所做的功,
因左图中金属块匀速直线运动时处于平衡状态,受到的摩擦力和绳子的拉力是一对平衡力,
所以,金属块受到的摩擦力f=F1,
所以,在使用滑轮的过程中拉力做的有用功W有=fL=F1L;
该滑轮的机械效率η===。
答:(1)图中金属块静放在地面时对地面的压强为;
(2)拉力在使用滑轮的过程中做的总功为2F2L;
(3)该滑轮的机械效率为。
29.(1)绳子自由端移动的距离8m;
(2)此过程中所做的额外功80J;
(3)此过程中所做的有用功720J;
(4)机械效率90%
【分析】(1)动滑轮绳子的有效股数为2,根据s=nh求出绳子自由端移动的距离;
(2)根据W额=G动h求出额外功的大小;
(3)根据W有=Gh求出有用功的大小;
(4)根据W总=W有+W额求出总功,根据机械效率公式求出机械效率的大小。
【解答】解:
(1)由图可知,n=2,物体上升h=4m,则绳子自由端移动的距离为:s=nh=2×4m=8m;
(2)由题意可知,不计绳重和摩擦,则此过程中所做的额外功为:W额=G动h=20N×4m=80J;
(3)此过程中所做的有用功为:W有=Gh=180N×4m=720J;
(4)总功为:W总=W有+W额=720J+80J=800J;
机械效率为:η==×100%=90%。
答:(1)绳子自由端移动的距离8m;
(2)此过程中所做的额外功80J;
(3)此过程中所做的有用功720J;
(4)机械效率90%。
30.(1)实心长方体浸没时受到的浮力为100N;
(2)实心长方体从水底到露出水面前,上升的高度为1.6m;
(3)实心长方体从水底到露出水面前,若人对绳的拉力F2做功400J,此过程中滑轮组的机械效率为80%。
【分析】(1)由图乙可知,物体浸没时,测力计示数F1=200N,当物体被拉出水面后,物体所受的拉力等于物体的重力,为G=300N,根据F浮=G﹣F1得出物体浸没在水中所受到的浮力;
(2)长方体从水底到刚好露出水面的运动时间为t=8s,根据h=vt得出长方体上升的高度;
(3)实心长方体从水底到露出水面前,根据W有用=F1h得出有用功,根据η=×100%得出此过程中滑轮组的机械效率。
【解答】解:(1)由图乙可知,物体浸没时,测力计示数F1=200N,
当物体被拉出水面后,物体所受的拉力等于物体的重力,为G=300N,
所以物体浸没在水中所受到的浮力为F浮=G﹣F1=300N﹣200N=100N;
(2)长方体从水底到刚好露出水面的运动时间为t=8s,
则长方体上升的高度为h=vt=0.2m/s×8s=1.6m;
(3)实心长方体从水底到露出水面前,有用功为W有用=F1h=200N×1.6m=320J,
此过程中滑轮组的机械效率为η=×100%=×100%=80%。
答:(1)实心长方体浸没时受到的浮力为100N;
(2)实心长方体从水底到露出水面前,上升的高度为1.6m;
(3)实心长方体从水底到露出水面前,若人对绳的拉力F2做功400J,此过程中滑轮组的机械效率为80%。
31.(1)绳子自由端移动的距离为6m,动滑轮的重为50N;
(2)工人做的有用功为1050J;
(3)工人做的额外功为150J;
(4)滑轮组的的机械效率为87.5%。
【分析】(1)根据滑轮组装置确定绳子股数,利用s=nh求出绳子自由端移动的距离;忽略摩擦及绳重,根据F=(G+G动)求出动滑轮的重;
(2)根据W有=Gh求出工人做的有用功;
(3)根据W总=Fs求出工人做的总功,利用W总=W有+W额求出额外功;
(4)根据η=求出滑轮组的的机械效率。
【解答】解:(1)由图可知,n=2,S=nh=2×3m=6m;
忽略摩擦及绳重,根据F=(G+G动)可知,动滑轮的重为:
G动=nF﹣G=2×200N﹣350N=50N;
(2)W有=Gh=350N×3m=1050J;
(3)W总=Fs=200N×6m=1200J,
W 额=W总﹣W有=1200J﹣1050J=150J;
(4)滑轮组的的机械效率为:
η=×100%=×100%=87.5%。
答:(1)绳子自由端移动的距离为6m,动滑轮的重为50N;
(2)工人做的有用功为1050J;
(3)工人做的额外功为150J;
(4)滑轮组的的机械效率为87.5%。
32.(1)动滑轮的重力G动为30N;
(2)当G物=120N时,若此时人在10s内将物体提升了2m,则此时拉力的功率为30W;
(3)若人站的位置能承受的最大压强为12500Pa,则该滑轮组所能提升物体的最大机械效率为90%
【分析】(1)不计绳重和摩擦,滑轮组的机械效率η=×100%=×100%=×100%=×100%,则动滑轮重G动=﹣G物;
(2)图乙中连接动滑轮的绳子股数n=3,不计绳重和摩擦,根据F′=×(G物′+G动)计算此时的拉力,根据W=Fs求出功的大小,根据P=求出功率的大小;
(3)当人站的位置承受的压强最大时,人对地面的压力最大,根据F压=pS计算,地面对人的支持力和人对地面的压力是相互作用力,大小相等,根据G=mg计算人的重力,人对绳的最大拉力F″=F支﹣G人,物体的最大重力G″=nF″﹣G动,滑轮组的最大机械效率根据η″=×100%计算。
【解答】解:(1)不计绳重和摩擦,滑轮组的机械效率η=×100%=×100%=×100%=×100%,则动滑轮重G动=﹣G物,
由图乙可知动滑轮的重力G动=﹣G物=﹣120N=30N;
(2)由图知,n=3,故自由端拉力为
自由端移动的距离为:s=3h=3×2m=6m;
拉力做的功为:W总=Fs=50N×6m=300J;
拉力的功率为:;
(3)人对地面的最大压力为:
地面对人的支持力等于人对地面的压力,即:F支=F压=500N;
人的重力为:G=m人g=40kg×10N/kg=400N,
故绳子的最大拉力为:Fm=F支﹣G=500N﹣400N=100N;
最大物重为Gm=3Fm﹣G动=3×100N﹣30N=270N;
此时机械效率最大,为:。
答:(1)动滑轮的重力G动为30N;
(2)当G物=120N时,若此时人在10s内将物体提升了2m,则此时拉力的功率为30W;
(3)若人站的位置能承受的最大压强为12500Pa,则该滑轮组所能提升物体的最大机械效率为90%。
33.(1)文物浸没在水中时受到的浮力是1×103N;
(2)动滑轮的重力是200N;
(3)在整个打捞过程中,a、b、c三根绳中a绳承受的拉力最大,该绳至少要承受5.1×103N的拉力。
【分析】(1)知道文物的体积,即浸没水中排开水的体积,利用阿基米德原理求文物受到的浮力;
(2)绳重、滑轮与轴的摩擦以及水的阻力均忽略不计,根据W有用=(G﹣F浮)h可求物体的重力G,再根据滑轮组的机械效率η===,据此求动滑轮重力;
(3)整个打捞过程中,若文物出水后,由图知,n=2,拉力F=(G+G动),即b根绳子承受的拉力;a点绳子的拉力Fa=2F+G定;c点绳子的拉力Fc=G;据此确定a、b、c三根绳中哪根绳承受的拉力最大及其大小。
【解答】解:
(1)文物浸没在水中时排开水的体积:
V排=V=100dm3=0.1m3,
则文物受到的浮力:
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×0.1m3=1×103N;
(2)因绳重、滑轮与轴的摩擦以及水的阻力均忽略不计,
由W有用=(G﹣F浮)h可得,物体的重力:
G=+F浮=+1×103N=4.8×103N,
则文物完全浸没在水中时,滑轮组的机械效率:
η====95%,
即:=95%,
解得动滑轮重力:G动=200N;
(3)整个打捞过程中,若文物出水后,
由图知,n=2,绳子自由端的拉力:
F=(G+G动)=×(4.8×103N+200N)=2.5×103N,
即b绳承受的拉力:Fb=F=2.5×103N;
a绳承受的拉力:Fa=2F+G定=2×2.5×103N+100N=5.1×103N;
c绳承受的拉力:Fc=G=4.8×103N;
可见,a、b、c三根绳中a绳承受的拉力最大,该绳至少要承受5.1×103N的拉力。
答:(1)文物浸没在水中时受到的浮力是1×103N;
(2)动滑轮的重力是200N;
(3)在整个打捞过程中,a、b、c三根绳中a绳承受的拉力最大,该绳至少要承受5.1×103N的拉力。
【计算7 杠杆的机械效率】
34.(1)杠杆自重为15N。
(2)杠杆提升重物的机械效率约为66.7%。
(3)若将动力作用点从B点移到C点,其它条件不变,杠杆的机械效率不变。
【分析】(1)根据杠杆的平衡条件算杠杆自重;
(2)根据公式η=计算效率;
(3)先算出改变后的效率,再进行比较。
【解答】解:(1)杠杆水平放置时,杠杆自重的力臂L3=OC;
设OA=L0,则OB=3L0,OC=4L0,故L3=OC=×4L0=2L0;
根据杠杆平衡条件可知:F OB=G OA+G杆L3;
F×3L0=60N×L0+G杆×2L0;
故3F=60N+2G杆;
解得:G杆=15N;
(2)因为OA:OB=1:3,故B点上升的高度是A点的3倍,
故机械效率为:
η===≈66.7%;
(3)若将动力作用点从B点移到C点时,因为OA:L3=1:2,所以杠杆重心上升的高度是物体上升高度的2倍;故:
η====≈66.7%;
答:(1)杠杆自重为15N。
(2)杠杆提升重物的机械效率约为66.7%。
(3)若将动力作用点从B点移到C点,其它条件不变,杠杆的机械效率不变。
35.(1)力F的大小为90N;
(2)将重物匀速提升时杠杆的机械效率为83.3%。
【分析】由题意可知,将挂在杠杆中点B的物体匀速缓慢提升至虚线位置时,这个过程中阻力臂与动力臂的比值始终等于杠杆在水平位置时阻力臂与动力臂的比值,知道动力臂、阻力臂、阻力,根据杠杆平衡条件F1×L1=F2×L2求出动力F;
由W=Gh可求得有用功,由W总=Fs可求得总功,由η=×100%可求得杠杆的机械效率。
【解答】解:用竖直向上的拉力F在A点,将挂在杠杆中点B的重为150N的物体匀速缓慢提升至虚线位置时,杠杆自身重力的作用点在中点,这个过程中阻力臂与动力臂的比值始终等于杠杆在水平位置时阻力臂与动力臂的比值,即比值始终为=,由杠杆平衡条件可得,F×L1=(G+G杆)×L2可知,竖直向上提升过程中动力F大小不变,
F×OA=(G+G杆)×OB可得,
F====90N;
此时杠杆所做的有用功W有用=Gh=150N×0.5m=75J,
此时杠杆所做的总功W总=Fs=90N×1m=90J,
杠杆的机械效率:
η=×100%=×100%≈83.3%。
答:(1)力F的大小为90N;
(2)将重物匀速提升时杠杆的机械效率为83.3%。
36.200;70。
【分析】(1)根据公式W=Fs可求总功;
(2)根据公式W=Gh可求有用功,有用功与总功的比值就是千斤顶的机械效率。
【解答】解:
(1)人做的功是总功:W总=Fs=100N×2m=200J;
(2)已知h=14cm=0.14m,所做的有用功:
W有用=Gh=1000N×0.14m=140J,
千斤顶的机械效率:
η=×100%=×100%=70%。
故答案为:200;70。
【计算8 斜面的机械效率】
37.(1)汽车从山底开到山顶所做的有用功为1.5×107J;
(2)山坡的机械效率为30%;
(3)汽车在山坡上行驶时的摩擦力为1.75×104N。
【分析】(1)利用W=Gh求汽车从山底开到山顶所做的有用功;
(2)利用W=Fs算出牵引力做的总功,山坡的机械效率等于有用功与总功之比;
(3)额外功等于总功减去有用功,再利用W额=fs求汽车在山坡上行驶时的摩擦力。
【解答】解:(1)货车从山底到山顶牵引力做的有用功:
W有用=Gh=5.0×104N×300m=1.5×107J;
(2)汽车从山底开到山顶所做的总功为:
W总=Fs=2.5×104N×2000m=5×107J;
山坡的机械效率为:
η==×100%=30%;
(3)货车上坡时所做的额外功,即克服摩擦力做的功为:
W摩=W总﹣W有用=5.0×107 J﹣1.5×107 J=3.5×107J,
由W额=fs可得,汽车在山坡上行驶时的摩擦力为:
货车上坡时的摩擦力f===1.75×104 N;
答:(1)汽车从山底开到山顶所做的有用功为1.5×107J;
(2)山坡的机械效率为30%;
(3)汽车在山坡上行驶时的摩擦力为1.75×104N。
38.(1)绳子拉力F对A所做的有用功为600J;
(2)该斜面的机械效率为80%;
(3)物体A受到的滑动摩擦力为30N。
【分析】(1)知道物体的重力、斜面高,根据W=Gh求绳子拉力F对物体A所做的有用功;
(2)由图知,n=2,不计绳重、滑轮与绳间的摩擦力、空气阻力,使用滑轮组的绳子自由端的拉力F=(GB+G动),力的作用是相互的,可求绳对A的拉力的大小,知道斜面长,根据W=Fs求出拉力对A所做的总功;斜面的机械效率等于有用功与总功之比;
(3)根据公式W额=W总﹣W有用求出额外功,在拉动物体A的过程中克服摩擦力做的功是额外功,根据公式W额=fs求出摩擦力的大小。
【解答】解:(1)绳子拉力F对物体A所做的有用功:W有用=GAh=200N×3m=600J,
(2)由图可知,物体A用细绳跨过滑轮组与物体B连起来,在动滑轮与重物B的作用下,能够使物体A由斜面底端被匀速拉到顶端,
不计绳重、滑轮组内部摩擦及空气阻力,对A的拉力大小等于使用滑轮组绳子自由端的拉力:
F=(GB+G动)=×(280N+20N)=150N;
拉力对A做的总功:W总=Fs=150N×5m=750J,
斜面机械效率:η=×100%=×100%=80%;
(3)拉力对物体A做的额外功:W额=W总﹣W有用=750J﹣600J=150J,
由W额=fs可得,A与斜面间的摩擦力大小为:
f===30N。
答:(1)绳子拉力F对A所做的有用功为600J;
(2)该斜面的机械效率为80%;
(3)物体A受到的滑动摩擦力为30N。
39.(1)斜面对木块的摩擦力为90N;
(2)斜面的机械效率是62.5%。
【分析】(1)斜面是用来提高物体位置的,有用功等于物体重力和斜面高度的乘积。
总功等于物体沿斜面向上的拉力和斜面长的乘积。
求出额外功,利用W额=fs求摩擦力。
(2)机械效率就是有用功和总功的比值。
【解答】解:(1)斜面是与水平面成30度的角,
h=L=×5m=2.5m,
W有用=Gh=300N×2.5m=750J,
总功W总=FL=240N×5m=1200J,
W额=W总﹣W有用=1200J﹣750J=450J,
f===90N;
(2)机械效率η=×100%=×100%=62.5%。
答:(1)斜面对木块的摩擦力为90N;
(2)斜面的机械效率是62.5%。
40.(1)箱子受到的重力为300N;
(2)箱子受到的摩擦力为30N;
(3)斜面的机械效率为80%;
(4)减小斜面的坡度、减小斜面的粗糙程度,都可以省力。
【分析】(1)知道箱子的质量,利用G=mg求箱子受到的重力;
(2)利用W=Fs求推力所做的总功,利用W=Gh求推力做的有用功,沿斜面推动箱子,克服斜面对箱子的摩擦力做的功是额外功,其大小等于总功减去有用功,再利用W额=fs求箱子受到的摩擦力;
(3)斜面的机械效率等于有用功与总功之比;
(4)使用斜面时,在斜面高一定时,斜面越长越省力;减小斜面的粗糙程度可以省力。
【解答】解:(1)箱子受到的重力:
G=mg=30kg×10N/kg=300N;
(2)推力所做的总功:W总=Fs=150N×3m=450J,
推力做的有用功:W有用=Gh=300N×1.2m=360J,
沿斜面推动箱子,克服斜面对箱子的摩擦力做的功是额外功,其大小为:
W额=W总﹣W有=450J﹣360J=90J,
由W额=fs可得箱子受到的摩擦力:
f===30N;
(3)斜面的机械效率:η=×100%=×100%=80%;
(4)减小斜面的坡度、减小斜面的粗糙程度,都可以省力。
答:(1)箱子受到的重力为300N;
(2)箱子受到的摩擦力为30N;
(3)斜面的机械效率为80%;
(4)减小斜面的坡度、减小斜面的粗糙程度,都可以省力。
同课章节目录
