专题05电路初探与欧姆定律(实验专题训练)(含解析)2024-2025学年九年级物理上学期期末复习专题训练(苏科版)
文档属性
| 名称 | 专题05电路初探与欧姆定律(实验专题训练)(含解析)2024-2025学年九年级物理上学期期末复习专题训练(苏科版) | 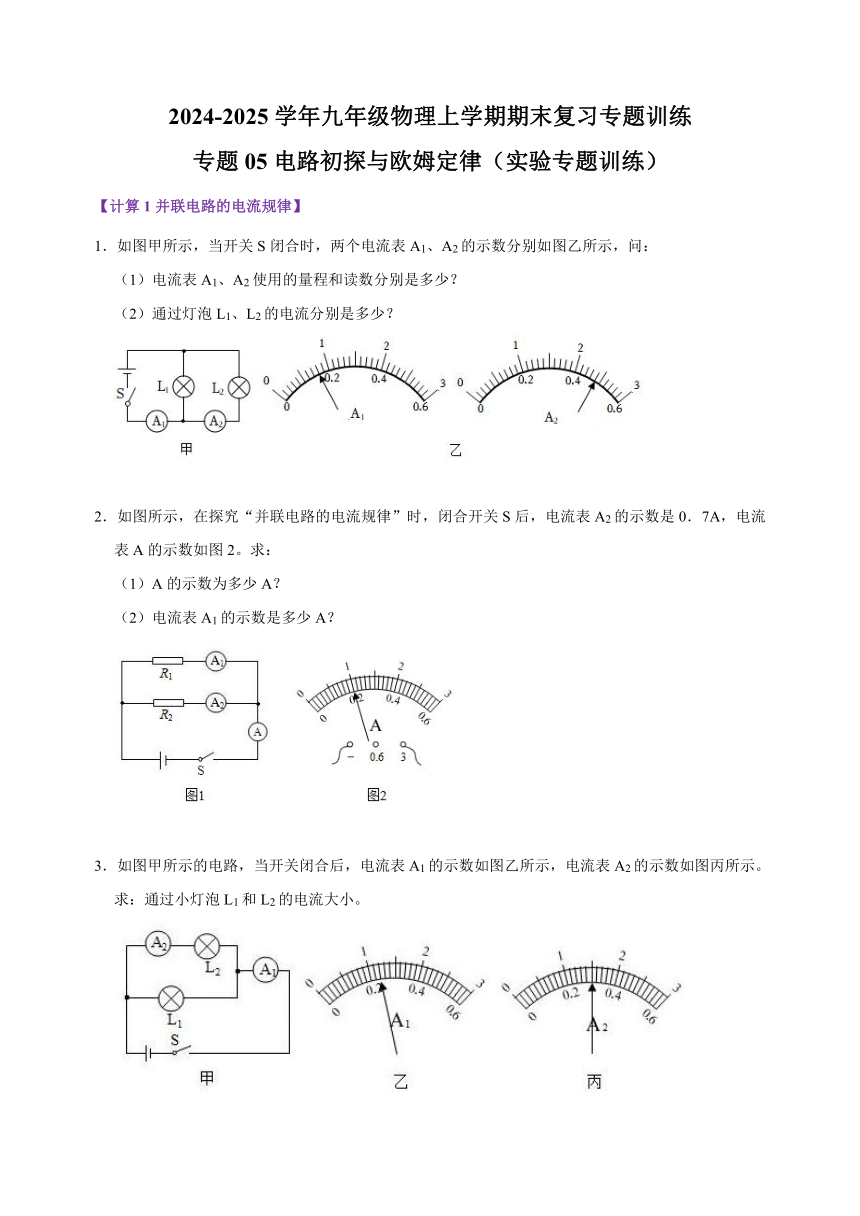 | |
| 格式 | docx | ||
| 文件大小 | 652.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-12 09:24:18 | ||
图片预览



文档简介
2024-2025学年九年级物理上学期期末复习专题训练
专题05电路初探与欧姆定律(实验专题训练)
【计算1并联电路的电流规律】
1.如图甲所示,当开关S闭合时,两个电流表A1、A2的示数分别如图乙所示,问:
(1)电流表A1、A2使用的量程和读数分别是多少?
(2)通过灯泡L1、L2的电流分别是多少?
2.如图所示,在探究“并联电路的电流规律”时,闭合开关S后,电流表A2的示数是0.7A,电流表A的示数如图2。求:
(1)A的示数为多少A?
(2)电流表A1的示数是多少A?
3.如图甲所示的电路,当开关闭合后,电流表A1的示数如图乙所示,电流表A2的示数如图丙所示。求:通过小灯泡L1和L2的电流大小。
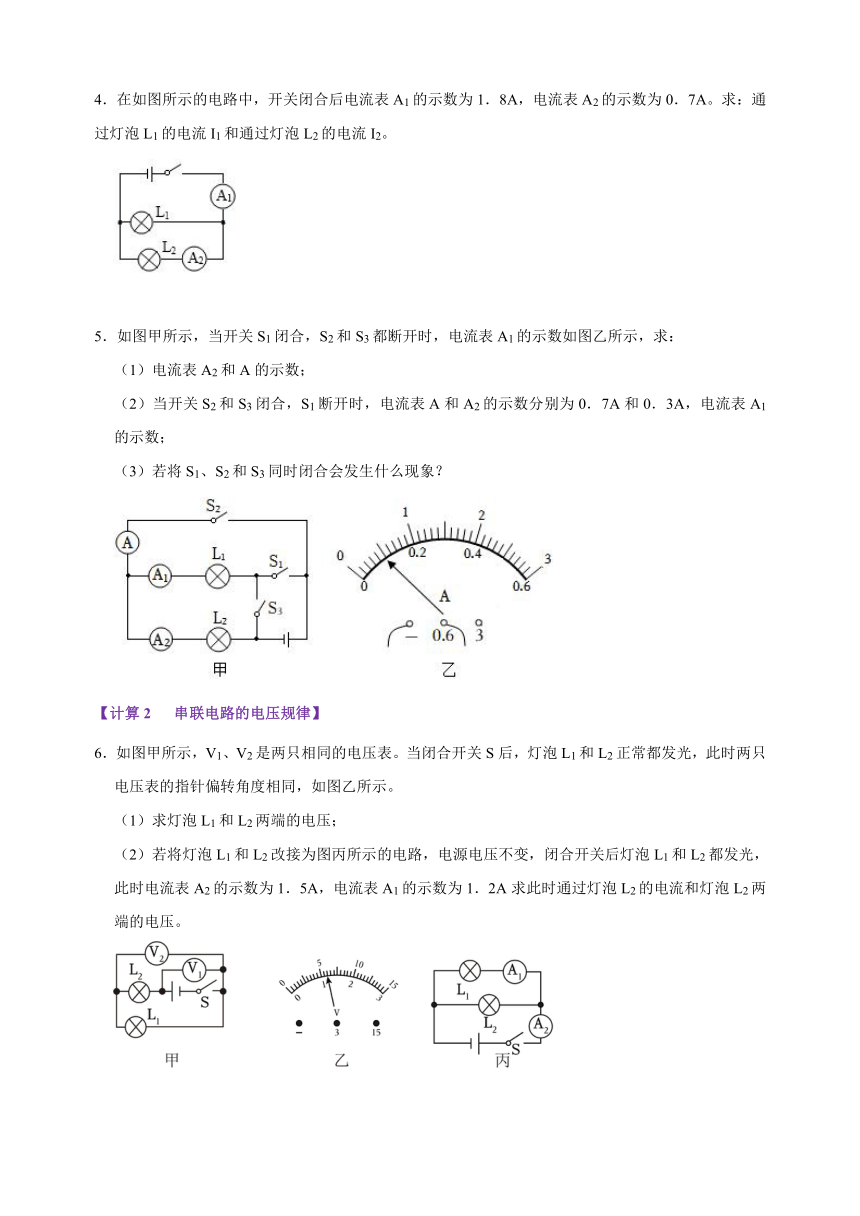
4.在如图所示的电路中,开关闭合后电流表A1的示数为1.8A,电流表A2的示数为0.7A。求:通过灯泡L1的电流I1和通过灯泡L2的电流I2。
5.如图甲所示,当开关S1闭合,S2和S3都断开时,电流表A1的示数如图乙所示,求:
(1)电流表A2和A的示数;
(2)当开关S2和S3闭合,S1断开时,电流表A和A2的示数分别为0.7A和0.3A,电流表A1的示数;
(3)若将S1、S2和S3同时闭合会发生什么现象?
【计算2 串联电路的电压规律】
6.如图甲所示,V1、V2是两只相同的电压表。当闭合开关S后,灯泡L1和L2正常都发光,此时两只电压表的指针偏转角度相同,如图乙所示。
(1)求灯泡L1和L2两端的电压;
(2)若将灯泡L1和L2改接为图丙所示的电路,电源电压不变,闭合开关后灯泡L1和L2都发光,此时电流表A2的示数为1.5A,电流表A1的示数为1.2A求此时通过灯泡L2的电流和灯泡L2两端的电压。
7.(1)在图甲所示的电路中,当开关S1、S2都闭合时,电流表的示数为0.58A;当开关S1断开、S2闭合时,电流表的示数为0.22A。请计算当开关S1、S2都闭合时通过电灯L1的电流。
(2)如图乙所示的电路,当开关S闭合后,电压表V1、V2的示数分别为2.2V和5.8V。请计算当开关S闭合时电灯L2两端的电压。
8.如图所示得测量电路中,闭合开关后电压表V1的示数为2V,V2的示数4V,求:
(1)电压表V的示数是多少?
(2)此电源需要几个干电池串联而成?
9.如图甲所示的电路中,电源由三节新干电池串联组成。闭合开关后,两灯泡均发光,电流表的示数如图乙所示,电压表V2指针如图丙所示。试求:
(1)电源电压是多少?
(2)流过灯L1和L2的电流分别是多少?
(3)L1和L2两端的电压分别是多少?
【计算3 欧姆定律公式的应用】
10.如图所示,R1=30Ω,闭合开关,电压表和电流表的示数分别为6V和0.5A.求:
(1)通过电阻R1的电流;
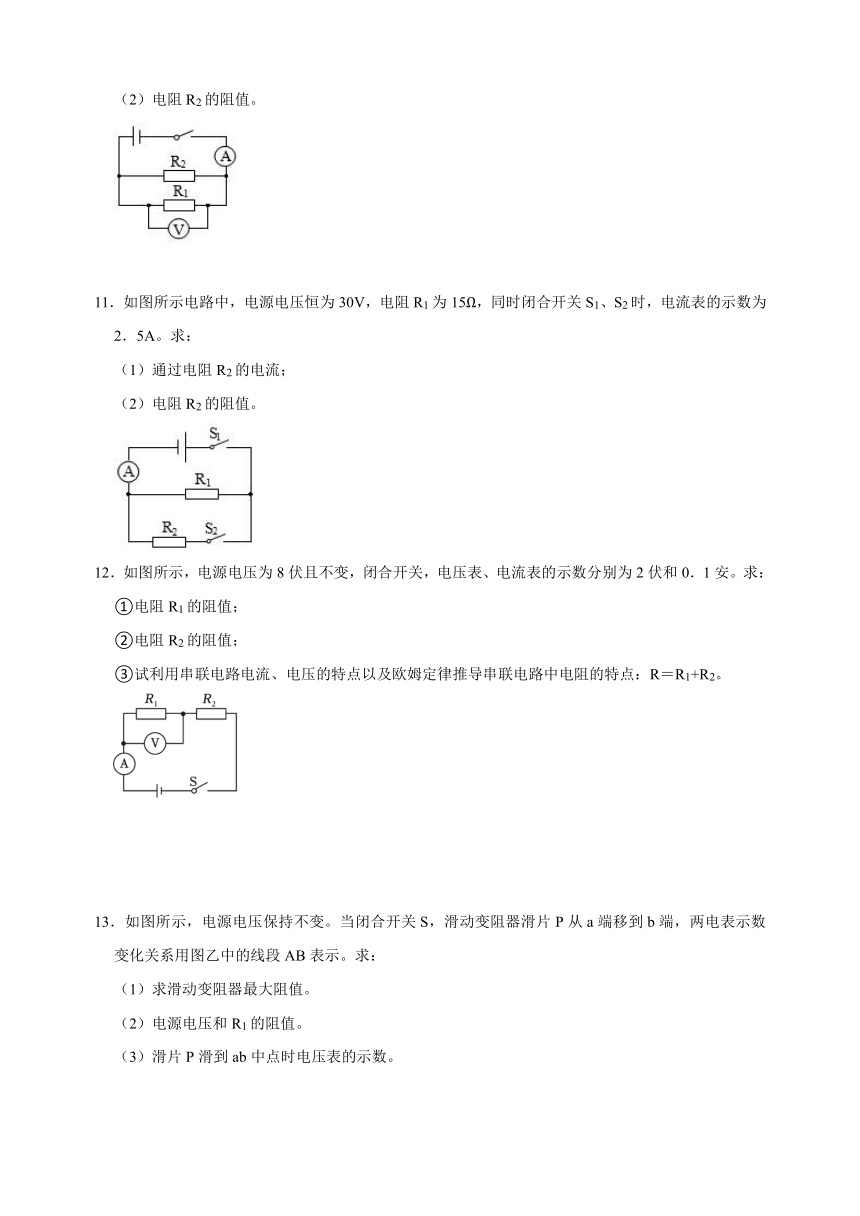
(2)电阻R2的阻值。
11.如图所示电路中,电源电压恒为30V,电阻R1为15Ω,同时闭合开关S1、S2时,电流表的示数为2.5A。求:
(1)通过电阻R2的电流;
(2)电阻R2的阻值。
12.如图所示,电源电压为8伏且不变,闭合开关,电压表、电流表的示数分别为2伏和0.1安。求:
①电阻R1的阻值;
②电阻R2的阻值;
③试利用串联电路电流、电压的特点以及欧姆定律推导串联电路中电阻的特点:R=R1+R2。
13.如图所示,电源电压保持不变。当闭合开关S,滑动变阻器滑片P从a端移到b端,两电表示数变化关系用图乙中的线段AB表示。求:
(1)求滑动变阻器最大阻值。
(2)电源电压和R1的阻值。
(3)滑片P滑到ab中点时电压表的示数。
14.如图1所示的电路中,电源电压为14伏保持不变。滑动变阻器标有“20欧 2安”字样,闭合开关S,电流表A的示数如图2所示。
①求此时滑动变阻器R连入电路的阻值。
②移动变阻器滑片P可以使电流表的最大值和最小电流。
15.新冠肺炎疫情期间,体温检测成为社区、商场等公共场所一种重要的防控手段。如图甲为某电子测温仪的内部简化电路图,测温仪探头内有一热敏电阻Rt,其阻值随温度变化关系如图乙所示。R1为阻值可调的电阻箱,其最大电阻为300Ω,允许通过的最大电流为0.02A,电流表的量程0~0.6A,电压表的量程是0﹣3V,电源电压恒定。某次测试时,将电阻箱的阻值调为R,发现电流表示数为0.01A,此时Rt两端电压为4V。
(1)此时电路中Rt的电阻是多少?
(2)当电流表示数为0.01A时,环境温度是多少?
(3)当环境温度为30℃,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,求电源电压是多少?
(4)若温度为40℃,则电阻箱允许接入电路的阻值调节范围是多少?
16.实际上电源内部都有一定的电阻,如干电池,我们需要用电压U和电阻r两个物理量来描述它。实际计算过程中,可以把它看成是由一个电压为U、电阻为0的理想电源与一个电阻值为r的电阻串联而成,如图甲所示。在图乙中,R1=9Ω,滑动变阻器R2的最大值为20Ω,闭合开关S,滑动变阻器的滑片从a调节到b的过程中,电流表示数变化范围为0.1A~0.3A,把电源按图甲中的等效方法处理(忽略电流表内阻影响)。求:
(1)电源电压U和电阻r;
(2)当滑动变阻器的滑片处于中点时,电源内阻r的电压和电流。
17.在如图所示的电路中,电源电压为16V不变,滑动变阻器R2上标有“27Ω 2A”的字样,闭合开关S后,电流表的示数为1A,电压表的示数为5V求:
(1)电阻R1的阻值;
(2)电路中的最小电流;
(3)在电压表和电流表不改变量程的情况下,为使电路正常工作,滑动变阻器R2连入电路的阻值范围。
18.如图所示电路,电源电压恒定为3V,R2=10Ω,当S1闭合,S2、S3断开,电流表示数为0.6A。
求:(1)R1阻值为多少?
(2)当S2闭合,S1、S3断开时,电压表示数为多少?
(3)当S1、S3闭合,S2断开时,电流表示数为多少?
19.如图所示的电路中,电源电压不变,已知定值电阻R1=20Ω,R2=40Ω,开关闭合后,电流表A1的示数为0.6A。求:
(1)电源电压;
(2)电流表A的示数。
20.随着我国经济的发展,人民生活水平日益提高,我国出现了越来越多的潜水爱好者。为了保障安全,潜水员潜水时会佩戴如图甲所示的水压表和深度表。图乙是某深度表的工作原理简化电路图,电源电压U=6V且恒定不变,定值电阻R0=15Ω,电压表量程为0 3V,Rp是阻值随水深度变化的电阻,其变化关系图象如图丙所示,Rp允许通过的最大电流为0.24A。求:
(1)深度表在水面上时,电路中的电流(计算结果保留1位小数);
(2)电压表示数为2V时,潜水员下潜的深度;
(3)在保证电路安全的情况下,该深度表能浸入水中的最大深度。
【计算4 欧姆定律与浮力杠杆的综合计算】
21.某物理兴趣小组设计了一套测量货车重力的模拟装置,工作原理如图所示。ABO为一水平杠杆,OA长1.2m,O为支点,AB:OB=5:1,平板上物体所受重力大小通过电压表读数显示。压力传感器R固定放置,R的阻值随所受压力F变化的关系如表所示。当电源电压U为12V,平板空载时,闭合开关S,电压表的示数为1.5V。平板、压杆和杠杆的质量均忽略不计。
F/N 0 4 8 12 16 20 23 …
R/Ω 70 60 50 40 30 20 12.5 …
(1)定值电阻R0的阻值;
(2)当平板上物体重120N时,电压表的示数;
(3)电池组用久后电源电压变小为9V,要求平板上重为120N的物体对应的电压表读数和电池组的电压U=12V的情况下相同,其它条件不变,只水平调节杠杆上触点B的位置即可实现,试判断并计算触点B应向哪个方向移动?移动多少距离?
22.某物理兴趣小组利用下列装置来测量物体M的密度,其部分结构如图甲所示。电源电压恒定,R0为10Ω的定值电阻,滑动变阻器R的阻值随弹簧的拉力F变化关系如图乙,T为容器的阀门。现将物体M悬挂于P点放入容器中,保持静止状态,打开阀门T,随着水缓慢注入容器,电压表示数U随容器中水的深度h变化关系如图丙中的实线所示。当水面深度到达h1时,电流表示数为0.4A(弹簧电阻忽略不计,物体M不吸水),求:
(1)电源电压和物体M所受的重力;
(2)当物体M完全浸没时所受的浮力;
(3)物体M的密度。
23.如图甲所示,恩西同学设计了一个汽车落水安全装置并进行了试验,在汽车的四个门板外侧分别安装一个气囊,气囊的触发由图乙所示电路中a、b间的电压来控制,压敏电阻R1水平安装在汽车底部A处,R1的阻值随其表面水的压力的变化如图丙所示。某次试验时:汽车入水前把R2的滑片调到合适位置不动,闭合开关S,电压表的示数为3V,再把汽车吊入足够高的长方体水池中缓慢下沉,直到a、b间的电压等于或大于3V时,气囊就充气打开,使汽车漂浮在水中,试验装置相关参数如表所示。
电源电压 4.5V
R1接触水的面积 15cm2
长方体水池底面积 20m2
(1)求汽车入水前电路中的电流;
(2)当汽车漂浮时,测得水池的水位比汽车入水前上升了9cm(水未进入车内),求汽车受到的重力;
(3)求气囊充气打开时汽车A处浸入水中的深度。
24.某量水仪的内部简化结构如图甲所示,木块A(底面积为0.01m2)通过一轻质绝缘细杆与轻质滑片P固定在一起。在检测量水仪时,发现滑动变阻器有一段金属丝发生短路,滑动变阻器的电功率P、电压表示数U与水深H的关系分别如图乙和丙所示。已知电源电压U0恒定不变,R2为定值电阻,R1的阻值与金属丝长度成正比(g取10N/kg,容器足够高,不计绝缘细杆、滑片的体积和自重及滑片处的摩擦)。求:
(1)当水深H=5cm时,水对容器底的压强。
(2)木块A的重力。
(3)图乙、丙中对应H0的值。
25.海南水利资源丰富,小明设计了如图甲所示的水文站测量昌化江水位的原理图。电源电压U=3V,定值电阻R0=10Ω,滑动变阻器R长20cm,最大阻值20Ω。且滑动变阻器的阻值随滑片P从最上端C位置移动到最下端D位置的过程中均匀变化(滑片P移动过程中摩擦不计)。弹簧下端悬挂一重力为50N的物体AB,其底面积为0.01m2、长为0.3m。弹簧伸长量与它受到拉力的关系如图乙所示(不计弹簧质量,连接弹簧两端的绝缘细绳不可伸长)。已知闭合开关S后,当物体AB上表面与水面相平时,滑片P刚好在滑动变阻器R的最上端C位置。g取10N/kg,ρ水=1×103kg/m3。求:
(1)当物体AB底面朝下放置在水平桌面上,对桌面产生的压强大小;
(2)当物体AB上表面与水面相平时,物体AB受到的浮力大小;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,滑动变阻器R连入电路的阻值大小;
(4)当水面从物体AB上表面逐渐下降至下表面刚好离开水面的过程中,弹簧伸长了多少cm?
26.图所示是某校科技小组制作的液体密度计的工作原理图,其中空桶重1N,测量时需将桶内注满液体。电源电压恒为12V,定值电阻R0的阻值为10Ω;电压表的量程为0~3V,表盘改造后可直接显示所测液体的密度值;滑动变阻器R2标有“24Ω 0.5A”的字样,R1为压敏电阻,其阻值与所受压力F变化关系如表所示(R1的阻值不为0)。在桶内注满水时,桶内水重恰为1N,闭合开关S,移动R 的滑片至位置M时,电压表的示数为1.5V。
R1/Ω 130 110 90 70 50 30 ..
F/N 0 0.5 1.0 0.5 2.0 2.5
(1)此时滑动变阻器R2接入电路中的阻值为多大?
(2)R2的滑片在位置M时,该液体密度计的“0”刻度线与电压表表盘多少伏的刻度线相对应?
(3)移动R2的滑片可以改变密度计的最大测量值(此时电压表指针满偏)。已知桶的容积为100mL,则该液体密度计的最大测量值为多少?(g取10N/kg)
27.如图是电子秤的内部电路,杠杆ABO始终处于水平位置,B是杠杆的中点,电源电压恒为15V,R2是阻值为6Ω的定值电阻,R1是压敏电阻,它的阻值随压力变化关系如表,当电压表的示数等于或大于3V时,电子秤会自动发出报警声。(杠杆、支架及托盘的重均忽略不计)
压力F/N 50 100 150 200 250 300
阻值R1/Ω 50 30 24 20 17 16
(1)当该电子秤恰好报警时,托盘所放物体的质量为多少?
(2)已知杠杆OA的长为40cm,欲使在托盘上所放物体的质量为50kg才报警。则托盘的支撑点B应向左还是向右移?移动的距离为多少?
28.某款水位测量仪原理如图甲,电源电压恒为15V,R2是阻值为10Ω的定值电阻,R1为竖直固定的光滑均匀金属棒,总电阻为20Ω,总长度为40cm。滑片P一端与R1无摩擦良好接触,另一端固定在轻质弹簧下端,中间部分与可伸缩的轻质导线M相连,弹簧的伸长量与所受的拉力关系如图乙所示。某次测试时,当弹簧下端不挂物体时,滑片P位于R1的最上端,当弹簧下端挂边长为20cm的立方体A时,滑片P位于R1的最下端,此时物体A的下端距容器底的距离h=10cm,往容器中加水,物体A会上升,当电压表的示数为7.5V时停止加水,g=10N/kg。求:
(1)物体A的重力;
(2)停止加水后物体A所受的浮力;
(3)停止加水后物体A底部所受液体压强;
(4)停止加水后容器底部所受液体压强。
29.小明在实验室寻得一个压敏电阻R,他设计了如图甲所示的装置探究R的电阻值随液体深度的变化关系。电源电压恒为12V,在R表面涂上绝缘漆并将其紧密嵌在底面积为300cm2、高为20cm的柱形储水箱底部,R上表面直接与水接触。先在水箱中注入12cm深的水,然后在水中放入一底面积为200cm2、高为10cm的柱体M,通过上提和下压M来改变水的深度,当M竖直地漂浮在水面时浸入水中的深度为6cm。根据实验数据描绘出R的阻值随水深h的变化关系如图乙所示。求:
(1)放入物体M前,电流表的示数;
(2)M漂浮在水中时所受到的浮力;
(3)当电流表的示数为0.3A时,物体M相对于漂浮在水中时移动的距离。
30.一力敏电阻通过轻质细杆与圆柱形物体A连接,力敏电阻所在电路图如图甲虚线框所示,其中电源电压为10V。R2为定值电阻。研究所得力敏电阻R1的阻值与所受力大小之间的关系如图乙所示。现将物体A缓慢放入高15cm,底面积为40cm2的圆柱形容器中,容器内装有深度为9cm的水。还未进入水中时,电流表示数I0=0.2A。当物体A一半体积浸入液体中时,电流为I1=0.4A。在物体缓慢下降到完全浸没过程中,发现电流先增大后减小,且此过程中电流表最大示数为I2=0.5A(整个过程水未溢出,细杆足够长,g取10N/kg)。求:
(1)未放入物体时,水对容器底的压强;
(2)R2的阻值;
(3)物体A的密度。
31.真真同学设计了一款弹力秤,用来测量某段时间的降雨量。其原理如图甲所示,它主要由轻质弹簧,轻质杠杆OAB,压力传感器R(电阻值随所受压力的大小发生变化的变阻器)和显示压力大小的仪器A(实质是电流表)等关键元件构成,其中OA:OB=1:2,已知压力传感器的电阻R与它所受的压杆压力F的关系如图乙所示。电源电压为6V且保持不变,真真将一个质量为600g,棱长为10cm的实心正方体木块悬挂在弹簧下端,静止时木块下表面距离空烧杯底正上方4cm处,若烧杯底面积为300cm2,轻质弹簧自然状态时长度为10cm,且弹簧每受到1N的力时长度变化0.5cm,杠杆始终水平。当水槽内收集一些水时;
(1)弹簧恰好处于自然状态,求此时通过仪器A的电流;
(2)若仪器A示数为0.2A时,求物体排开水的体积V排;
(3)仪器A示数为0.2A时,求水槽中水的总质量。
32.如图甲所示,小王同学设计了一个汽车落水安全装置并进行了试验,在汽车的四个门板外侧分别安装一个气囊,气囊的触发由图乙所示电路中a、b间的电压来控制,压敏电阻R1水平安装在汽车底部A处,R1的阻值随其表面水的压力的变化如图丙所示。
某次试验时:汽车入水前把R2的滑片调到合适位置不动,闭合开关S,电压表的示数为4V,再把汽车吊入足够高的长方体水池中缓慢下沉,直到a、b间的电压等于或大于4V时,气囊就充气打开,使汽车漂浮在水中,试验装置相关参数如表所示。
电源电压 6V
R1接触水的面积 15cm2
长方体水池底面积 25m2
(1)求汽车入水前电路中R1的电流;
(2)当汽车漂浮时,测得水池的水位比汽车入水前上升了10cm(水未进入车内),求汽车受到的重力;
(3)求气囊充气打开时汽车A处浸入水中的深度。
参考答案
【计算1并联电路的电流规律】
1.(1)电流表A1使用0~3A量程,示数为0.8A,A2使用0~0.6A量程,示数为0.48A;
(2)通过灯泡L1、L2的电流分别为0.32A、0.48A。
【分析】(1)对于电流表的读数,应结合电联电路的电流特点确定量程,再根据指针位置读出示数。
(2)分析电路图可知,灯L1和L2组成并联电路,电流表A1测通过干路的电流,电流表A2测通过灯L2的电流,在并联电路中干路中的电流等于各支路电流之和。
【解答】解:
(1)由图甲知,电流表A1测的是干路电流,电流表A2测的是灯L2支路的电流,由于并联电路干路电流等于各支路电流之和,则电流表A1的示数应大于电流表A2的示数;
由图乙知,电流表A1指针偏转角度小于A2,
所以电流表A1选择的量程是0~3A,读数是0.8A,即干路电流:I=0.8A,
电流表A2的量程是0~0.6A,读数是0.48A,即通过灯L2的电流大小为:I2=0.48A,
(2)由于并联电路干路电流等于各支路电流之和,则通过灯L1的电流大小为:I1=I﹣I2=0.8A﹣0.48A=0.32A。
答:(1)电流表A1使用0~3A量程,示数为0.8A,A2使用0~0.6A量程,示数为0.48A;
(2)通过灯泡L1、L2的电流分别为0.32A、0.48A。
2.(1)A的示数为1A;(2)电流表A1的示数是0.3A
【分析】由图知,两电阻并联,A1测R1支路的电流,电流表A2测R2支路的电流,电流表A测干路电流,由图2得出电流表A的示数,根据并联电路中干路电流等于各支路电流之和即可解答。
【解答】解:(1)由图知,两电阻并联,A1测L1支路的电流,电流表A2测L2支路的电流,电流表A测干路电流,
由图2可得:电流表A的量程为0~3A,则示数为1A:即:干路电流I=1A;
(2)因并联电路中干路电流等于各支路电流之和,所以电流表A1的示数:I1=I﹣I2=1A﹣0.7A=0.3A。
答:(1)A的示数为1A;(2)电流表A1的示数是0.3A。
3.流过电灯L1的电流是0.9A,流过电灯L2的电流为0.3A。
【分析】(1)根据图示可知,灯L1与灯L2并联,电流表A1测干路电流,电流表A2测L2电流。
(2)电流表量程不明,但根据电流表连入电路情况知,A1电流表测量干路的电流I,电流表A2测量通过支路L2的电流I2.A1的示数应大于A2的示数。
(3)根据指针的偏转情况可以判断A用的是0~3A的量程,A2用的是0~0.6A的量程。通过观察指针所指位置即可读数,然后利用并联电路电流规律:I=I1+I2,可求出电灯L1的电流。
【解答】解:(1)由图可知:灯L1与灯L2并联,电流表A1测干路电流,电流表A2测L2电流。
根据并联电路电流规律可知:干路电流大于支路电流。而从两表指针偏转位置来看,A2偏转的比A1还大,说明这两表使用的量程不同。由此得出:A2的量程为0~0.6A量程,A1的量程为0~3A量程。
0~0.6A量程的分度值是0.02A,所以A2的示数是0.3A,即I2=0.3A。
0~3A量程的分度值是0.1A,所以A1的示数是1.2A;即I=1.2A,
(2)根据并联电路电流规律:I=I1+I2,所以通过灯L1的电流:I1=I﹣I2=1.2A﹣0.3A=0.9A。
答:流过电灯L1的电流是0.9A,流过电灯L2的电流为0.3A。
4.通过灯泡L1的电流I1为1.1A,通过灯泡L2的电流I2为0.7A。
【分析】分析电路图可知,灯L1和L2组成并联电路,电流表A1测通过干路的电流,电流表A2测通过灯L2的电流,在并联电路中干路中的电流等于各支路电流之和,据此解答。
【解答】解:由图可知L1、L2并联,
电流表A1测干路电流:I=1.8A,
电流表A2测L2的电流:即I2=0.7A,
因为在并联电路中干路中的电流等于各支路电流之和,
所以流过L1的电流I1=I﹣I2=1.8A﹣0.7A=1.1A。
答:通过灯泡L1的电流I1为1.1A,通过灯泡L2的电流I2为0.7A。
5.(1)电流表A2的示数为0.1A,A3的示数为0A;
(2)电流表A1的示数为0.4A;
(3)若将S1、S2和S3同时闭合会发生电源短路现象。
【分析】(1)当S1闭合、S2和S3都断开时,两灯串联,电流表A1、A2测电路中的电流,由串联电路的电流特点可知A2和A1的示数;
(2)当S2和S3闭合、S1断开时,两灯并联,电流表A测干路电流,A1、A2分别测L1和L2支路的电流,由并联电路的电流特点可得A1示数;
(3)不经过用电器而直接跟电源两极相连的电路叫做电源短路。
【解答】解:
(1)根据电路图可知,当S1闭合、S2和S3都断开时,L1、L2串联,电流表A1和A2都测量电路中的电流,
电流表A1的示数如图乙所示,该电流表选用小量程,分度值为0.02A,则A1的示数为0.1A,
因串联电路中电流处处相等,故电流表A1和A2的示数相等,都等于0.1A;电流表A处于断路状态,因此其示数为0A;
(2)当S2和S3闭合、S1断开时,两灯并联,电流表A测干路电流,A1、A2分别测L1和L2支路的电流,
因并联电路中干路电流等于各支路电流之和,
所以当S2和S3闭合、S1断开时,电流表A1的示数:IA1=IA﹣IA2=0.7A﹣0.3A=0.4A;
(3)当S1、S2和S3同时闭合时,电流从电源正极流出,直接从S1、S3回到电源负极,故发生电源短路,电源将被烧坏。
答:(1)电流表A2的示数为0.1A,A的示数为0A;
(2)电流表A1的示数为0.4A;
(3)若将S1、S2和S3同时闭合会发生电源短路现象。
【计算2 串联电路的电压规律】
6.(1)L1两端电压为1.2V,L2两端的电压为4.8V;
(2)通过L2的电流为0.3A,L2两端的电压为6V。
【分析】(1)由图甲所示电路图可知,两灯泡串联,电压表V1测电源电压,电压表V2测L1两端电压;
根据电压表所测电路电压与指针偏转情况确定两电压表量程,读出其示数,然后求出两灯泡两端电压;
(2)由图丙所示电路可知,两灯泡并联,电流表A1测L1支路电流,电流表A2测干路电流,由并联电路特点求出通过灯泡的电流、求出灯泡两端电压。
【解答】解:
(1)由图甲所示电路图可知,两灯泡串联,电压表V1测电源电压,电压表V2测L1两端电压;
串联电路总电压大于部分电路电压,由图乙所示电压表可知,两电压表指针位置相同,
则电压表V1的量程为0~15V,示数为6V,电压表V2的量程为0~3V,示数为1.2V;
则灯L1两端电压为1.2V,灯L2两端电压:
U2=U﹣U1=6V﹣1.2V=4.8V;
(2)由图丙所示电路可知,两灯泡并联,电流表A1测L1支路电流,电流表A2测干路电流,
通过L2的电流:
I2=I﹣I1=1.5A﹣1.2A=0.3A,
灯L2并联在电源两端,电源电压为6V,则L2两端电压为6V。
答:(1)L1两端电压为1.2V,L2两端的电压为4.8V;
(2)通过L2的电流为0.3A,L2两端的电压为6V。
7.(1)当开关S1、S2都闭合时通过电灯L1的电流。为0.36A;
(2)当开关S闭合时电灯L2两端的电压为3.6V。
【分析】(1)当开关S1、S2都闭合时,两灯泡并联接入电路,电流表测干路电流,当开关S1断开、S2闭合时,电路为灯泡L2的简单电路,电流表测通过电路的电流,根据并联电路电流规律计算当开关S1、S2都闭合时通过电灯L1的电流;
(2)当开关S闭合后,两灯泡串联接入电路,电压表V1测灯泡L1两端的电压,电压表V2测电源电压,根据串联电路电压规律计算当开关S闭合时电灯L2两端的电压。
【解答】解:(1)当开关S1、S2都闭合时,两灯泡并联接入电路,电流表测干路电流,电流表的示数为0.58A;
当开关S1断开、S2闭合时,电路为灯泡L2的简单电路,电流表测通过电路的电流,电流表的示数为0.22A,
根据并联电路不相互影响,通过L2的电流不变,
并联电路干路电流等于各支路电流之和,所以当开关S1、S2都闭合时通过电灯L1的电流:I1=I﹣I2=0.58A﹣0.22A=0.36A;
(2)当开关S闭合后,两灯泡串联接入电路,电压表V1测灯泡L1两端的电压,电压表V2测电源电压,
串联电路总电压等于各部分电压之和,电压表V1、V2的示数分别为2.2V和5.8V,
则当开关S闭合时电灯L2两端的电压:U2=U﹣U1=5.8V﹣2.2V=3.6V。
答:(1)当开关S1、S2都闭合时通过电灯L1的电流。为0.36A;
(2)当开关S闭合时电灯L2两端的电压为3.6V。
8.(1)电压表V的示数是6V;
(2)此电源需要4个干电池串联而成.。
【分析】串联电路两端电压等于各部分电压之和,一节干电池的电压为1.5V。
【解答】解:图中,两个灯泡串联,电压表V1测L1两端电压,电压表V2测量L2两端电压,电压表V测量电源电压;因为串联电路两端电压等于各部分电压之和,因此V的示数为2V+4V=6V;而一节干电池电压为1.5V,因此需要4节干电池串联连接。
答:(1)电压表V的示数是6V;
(2)此电源需要4个干电池串联而成.。
9.(1)电源电压是4.5V;
(2)流过灯L1和L2的电流都是0.24A;
(3)L1和L2两端的电压分别是3.3V和1.2V。
【分析】(1)一节新干电池的电压为1.5V,电源由三节新干电池串联组成,据此计算电源电压;
(2)由乙图可知电流表接入电路的量程和分度值,闭合开关,两灯泡串联接入电路,根据串联电路电流特点可知流过灯L1和L2的电流分别是多少;
(3)电压表与所测灯泡并联接入电路,电压表V1测电源电压,电压表V2测灯泡L1两端的电压,分析电压表接入电路的量程,明确电压表的分度值,根据串联电路电压规律计算灯L2两端的电压。
【解答】解:(1)电源由三节新干电池串联组成,所以电源电压为:U=3×1.5V=4.5V;
(2)闭合开关,两灯泡串联接入电路,串联电路各处电流相等,电流表测通过电路的电流,由乙图可知电流表接入电路的量程为0~0.6A,分度值为0.02A,示数为0.24A,所以流过灯L1和L2的电流都是0.24A;
(3)电压表V1测电源电压,电压表V2测灯泡L2两端的电压,则电压表V2接入电路的量程为0~3V,分度值为0.1V,示数为1.2V,
串联电路总电压等于各部分电压之和,所以灯L1两端的电压为:U1=U﹣U2=4.5V﹣1.2V=3.3V。
答:(1)电源电压是4.5V;
(2)流过灯L1和L2的电流都是0.24A;
(3)L1和L2两端的电压分别是3.3V和1.2V。
【计算3 欧姆定律公式的应用】
10.见试题解答内容
【分析】由电路图可知,R1与R2并联,电压表测电源的电压,电流表测干路电流。
(1)根据并联电路的电压特点和欧姆定律求出通过电阻R1的电流;
(2)根据并联电路的电流特点求出通过R2的电流,根据欧姆定律求出电阻R2的阻值。
【解答】解:由电路图可知,R1与R2并联,电压表测电源的电压,电流表测干路电流。
(1)因并联电路中各支路两端的电压相等,
所以,通过电阻R1的电流:
I1===0.2A。
(2)因并联电路中干路电流等于各支路电流之和,
所以,通过R2的电流:
I2=I﹣I1=0.5A﹣0.2A=0.3A,
由欧姆定律得,电阻R2的阻值:
R2===20Ω。
答:(1)通过电阻R1的电流为0.2A;
(2)电阻R2的阻值为20Ω。
11.(1)通过电阻R2的电流为0.5A;
(2)电阻R2的阻值为60Ω。
【分析】(1)由电路图可知,同时闭合开关S1、S2时,R1、R2并联,电流表测干路中的电流,根据欧姆定律求出通过电阻R1的电流,根据并联电路中干路电流等于各支路电流之和求出通过电阻R2的电流;
(2)根据I=求出电阻R2的阻值。
【解答】解:(1)由电路图可知,同时闭合开关S1、S2时,R1、R2并联,电流表测干路中的电流,
则通过电阻R1的电流:
I1===2A;
根据并联电路中干路电流等于各支路电流之和知通过电阻R2的电流为:
I2=I﹣I1=2.5A﹣2A=0.5A;
(2)根据I=得电阻R2的阻值:
R2===60Ω。
答:(1)通过电阻R2的电流为0.5A;
(2)电阻R2的阻值为60Ω。
12.①电阻R1的阻值是20Ω;②电阻R2的阻值是60Ω;③推导过程见解答过程。
【分析】由电路图知两电阻串联,电流表测量电路的电流,电压表测量R1两端电压;
①根据欧姆定律计算电阻R1的阻值;
②根据串联电路电压特点和欧姆定律计算电阻R2的阻值;
③根据串联电路电流、电压特点和欧姆定律推导串联电路总电阻。
【解答】解:
①由电路图知两电阻串联,且I=I1=I2=0.1A,U1=2V,则R1===20Ω;
②由串联电路电压特点得,U2=U﹣U1=8V﹣2V=6V,则R2===60Ω;
③设电阻R1两端的电压为U1,电阻R2两端的电压为U2,电阻R1、R2两端的总电压为U,电阻R1、R2的总电阻为R,由于电阻R1、R2串联,通过两电阻的电流相等,设电路中的电流为I,
则由I=得:U1=R1I1=R1I,U2=R2I2=R2I,U=RI,
由串联电路的电压规律可知U=U1+U2,
即RI=R1I1+R2I2=R1I+R2I
所以R=R1+R2。
答:①电阻R1的阻值是20Ω;②电阻R2的阻值是60Ω;③推导过程见解答过程。
13.(1)滑动变阻器最大阻值为20Ω;
(2)电源电压为6V,R1的阻值为10Ω;
(3)滑片P滑到ab中点时电压表的示数为3V。
【分析】由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(1)当滑动变阻器滑片P在a端时,滑动变阻器接入电路中的电阻最大,电路中的电流最小,根据图乙读出电路中的最小电流和电压表的示数,根据欧姆定律求出滑动变阻器的最大阻值;
(2)当滑动变阻器滑片P在a端时,根据串联电路的电压特点和欧姆定律表示出电源的电压;当滑动变阻器滑片P在b端时,接入电路中的电阻为零,此时电路中的电流最大,根据图乙读出电路中的最大电流,利用欧姆定律求出电源的电压,然后联立等式求出R1的阻值和电源的电压;
(3)当滑片P滑到ab中点时,根据电阻的串联和欧姆定律求出电路中的电流,利用欧姆定律求出电压表的示数。
【解答】解:由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(1)当滑动变阻器滑片P在a端时,滑动变阻器接入电路中的电阻最大,电路中的电流最小,
由图乙可知,电路中的最小电流I小=0.2A,电压表的示数U2=4V,
由I=可知,滑动变阻器的最大阻值:R2===20Ω;
(2)当滑动变阻器滑片P在a端时,
因串联电路中总电压等于各分电压之和,所以,电源的电压U=I小R1+U2=0.2A×R1+4V﹣﹣﹣﹣﹣①
当滑动变阻器滑片P在b端时,接入电路中的电阻为零,此时电路中的电流最大,
由图乙可知,电路中的最大电流I大=0.6A,
则电源的电压U=I大R1=0.6A×R1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
由①②可得:R1=10Ω,U=6V;
(3)当滑片P滑到ab中点时,接入电路中的电阻R2′=R2=×20Ω=10Ω,
因串联电路中总电阻等于各分电阻之和,所以,电路中的电流I====0.3A,
则电压表的示数U2′=IR2′=0.3A×10Ω=3V。
答:(1)滑动变阻器最大阻值为20Ω;
(2)电源电压为6V,R1的阻值为10Ω;
(3)滑片P滑到ab中点时电压表的示数为3V。
14.①此时滑动变阻器R连入电路的阻值为17.5Ω。
②移动变阻器滑片P可以使电流表的最大值和最小电流分别为2A、0.7A。
【分析】①由电路图可知,只有R连入电路,电流表测电路中的电流,利用欧姆定律求出滑动变阻器R连入电路的阻值。
②根据图可知电流表的量程和滑动变阻器的规格即可判断电路中的最大电流;
当滑动变阻器接入电路的电阻最大时,电路中的电流最小;根据欧姆定律求出电路最小电流。
【解答】解:
①由电路图可知,只有R连入电路,电流表测电路中的电流,
由图2可知:电流表的量程是0~3A,则示数为0.8A,
由欧姆定律可得,滑动变阻器R连入电路的阻值:R′===17.5Ω;
②由于电流表的量程是0~3A,滑动变阻器标有“20欧 2安”字样
则电路中的最大电流为2A;
当滑动变阻器接入电路的电阻最大时,由欧姆定律可知通过电路的电流最小,
最小电流为:I小===0.7A。
答:①此时滑动变阻器R连入电路的阻值为17.5Ω。
②移动变阻器滑片P可以使电流表的最大值和最小电流分别为2A、0.7A。
15.(1)此时电路中Rt的电阻是400Ω;
(2)当电流表示数为0.01A时,环境温度是20℃;
(3)当环境温度为30℃,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,电源电压是6V;
(4)若温度为40℃,则电阻箱允许接入电路的阻值调节范围是100Ω~200Ω。
【分析】根据电路图可知,R1、Rt串联,电流表测量电路电流。
(1)(2)根据欧姆定律求出电阻箱接入电路的阻值;根据串联电路电压规律求出Rt两端电压,再根据欧姆定律求出Rt的阻值,并从图乙中读出此时的环境温度;
(3)由图乙可知,环境温度为40℃时热敏电阻的阻值,根据电流表的量程得出电路中的最大电流,根据欧姆定律求出电路的最小总电阻,利用电阻的串联求出电阻箱接入电路中的最小阻值,然后得出电阻箱允许的阻值调节范围。
【解答】解:由电路图可知,R1与Rt串联,电流表测电路中的电流。
(1)根据欧姆定律可知此时电路中Rt的电阻:Rt===400Ω;
(2)当电流表示数为0.01A时,Rt的电阻为400Ω,从图乙可知环境温度是20℃;
(3)设电源电压为U,则U=+,
当电流表示数为0.01A时,U=0.01A×R+4V…①
当环境温度为30℃,从图乙可知Rt的阻值为300Ω,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,
则:U=0.015A×0.5R+0.015A×300Ω…②
由①②解出解出U=6V;
(4)由图乙可知,环境温度为40℃时,热敏电阻的阻值Rt=200Ω,
由电流表的量程为0~0.6A和电阻箱允许通过的最大电流为0.02A可知,电路中的最大电流I大=0.02A,
则电路的最小总电阻:R总′===300Ω,
所以,电阻箱接入电路中的最小阻值:R1′=R总′﹣Rt=300Ω﹣200Ω=100Ω,
电压表的量程是0﹣3V,故电阻箱两端的电压最大为3V,此时Rt两端的电压为=6V﹣3V=3V,
根据欧姆定律及串联分压特点可知,电路中电流I小===0.015A,
此时变阻器接入电路的阻值最大,为R1″===200Ω,
则电阻箱允许接入电路的阻值调节范围是100Ω~200Ω。
答:(1)此时电路中Rt的电阻是400Ω;
(2)当电流表示数为0.01A时,环境温度是20℃;
(3)当环境温度为30℃,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,电源电压是6V;
(4)若温度为40℃,则电阻箱允许接入电路的阻值调节范围是100Ω~200Ω。
16.(1)电源电压U为3V,电源内阻r为1Ω;
(2)当滑动变阻器的滑片处于中点时,电源内阻r的电压为0.15V,通过电源内阻r的电流为0.15A。
【分析】(1)如图乙所示,电阻R1、滑动变阻器R2、电源内部电阻r三者串联。
当滑动变阻器位于a点时,根据欧姆定律电源电压U=Ia(R1+R2+r)①,
当滑动变阻器位于b点时,根据欧姆定律电源电压U=Ib(R1+r)②,
①②式联立求出电源电压U和电阻r;
(2)根据欧姆定律I=计算滑动变阻器的滑片处于中点时电路中的电流,根据欧姆定律U=IR计算电源内阻r的电压。
【解答】解:(1)如图乙所示,电阻R1、滑动变阻器R2、电源内部电阻r三者串联。
当滑动变阻器位于a点时,滑动变阻器完全接入电路,此时电路电流最小为0.1A,R1=9Ω,滑动变阻器R2的最大值为20Ω,
根据欧姆定律可得,电源电压U=Ia(R1+R2+r)=0.1A×(9Ω+20Ω+r)……①,
当滑动变阻器位于b点时,滑动变阻器不接入电路,此时电路电流最大为0.3A,
根据欧姆定律可得,电源电压U=Ib(R1+r)=0.3A×(9Ω+r)……②,
①②式联立解得,电源电压U=3V,电源内阻r=1Ω;
(2)当滑动变阻器的滑片处于中点时,接入电路的阻值为10Ω,根据欧姆定律可得,
此时电路中的电流I====0.15A,
串联电路电流相等,故通过电源内阻r的电流为0.15A,
电源内阻r的电压Ur=Ir=0.15A×1Ω=0.15V。
答:(1)电源电压U为3V,电源内阻r为1Ω;
(2)当滑动变阻器的滑片处于中点时,电源内阻r的电压为0.15V,通过电源内阻r的电流为0.15A。
17.见试题解答内容
【分析】由电路图可知,R1与R2串联,电压表测R1两端的电压,电流表测电路中的电流。
(1)根据欧姆定律求出电阻R1的阻值;
(2)当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,根据电阻的串联和欧姆定律求出电路中的最小电流;
(3)根据滑动变阻器的铭牌可知电路中的最大电流,根据欧姆定律求出电路中的总电阻,利用电阻的串联求出R2的最小阻值,然后得出滑动变阻器R2连入电路的阻值范围。
【解答】解:由电路图可知,R1与R2串联,电压表测R1两端的电压,电流表测电路中的电流。
(1)由I=可得,电阻R1的阻值:
R1===5Ω;
(2)当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,
因串联电路中总电阻等于各分电阻之和,
所以,电路中的最小电流:
I小===0.5A;
(3)由题意可知,电流表量程为0~3A,而滑动变阻器允许通过的最大电流为2A,
所以,为了保证电路的安全,电路中的最大电流I大=2A,此时变阻器接入电路中的电阻最小,
此时电路中的总电阻:
R===8Ω,
则滑动变阻器接入电路中的最小阻值:
R2小=R﹣R1=8Ω﹣5Ω=3Ω,
当变阻器接入电路中的电阻最大为27Ω时,电路中电流最小,电压表示数最小,各电路元件是安全的,
所以变阻器R2的阻值范围为3Ω~27Ω。
答:(1)电阻R1的阻值为5Ω;
(2)电路中的最小电流为0.5A;
(3)滑动变阻器R2连入电路的阻值范围为3Ω~27Ω。
18.(1)R1阻值为5Ω;
(2)当S2闭合,S1、S3断开时,电压表示数为2V;
(3)当S1、S3闭合,S2断开时,电流表示数为0.6A。
【分析】(1)当S1闭合,S2、S3断开时,只有R1连入电路中,根据欧姆定律计算R1的阻值;
(2)当S2闭合,S1、S3断开时,R1与R2串联,电压表V测测R2两端的电压,根据串联电路的电阻规律和欧姆定律计算通过电路的电流,根据U=IR计算电压表的示数;
(3)当开关S1、S3闭合,S2断开时,R1与R2并联,电流表测通过R1的电流,根据并联电路电压特点结合欧姆定律计算通过R1的电流,进一步确定电流表示数。
【解答】解:(1)由电路图知,当S1闭合,S2、S3断开时,只有R1连入电路中,电流表测通过R1的电流,
由欧姆定律可得R1阻值为:R1===5Ω;
(2)由电路图知,当S2闭合,S1、S3断开时,R1与R2串联,电压表V测R2两端的电压,电流表测量电路的电流,
串联电路总电阻等于各部分电阻之和,则电路总电阻:R=R1+R2=5Ω+10Ω=15Ω,
根据欧姆定律可得通过电路的电流为:I′===0.2A,
则电阻R1两端的电压:U1=I′R2=0.2A×10Ω=2V,即电压表示数为2V;
(3)当开关S1、S3闭合,S2断开时,R1与R2并联,电流表测通过R1的电流,
并联电路各支路两端电压相等,根据欧姆定律可得通过R1的电流:I1===0.6A,即电流表示数为0.6A。
答:(1)R1阻值为5Ω;
(2)当S2闭合,S1、S3断开时,电压表示数为2V;
(3)当S1、S3闭合,S2断开时,电流表示数为0.6A。
19.(1)电源电压为12V;
(2)电流表A的示数为0.9A。
【分析】由电路图可知,R1与R2并联,电流表A测干路电流,电流表A1测R1支路的电流。
(1)根据并联电路的电压特点结合欧姆定律求出电源电压;
(2)根据并联电路的电流规律结合欧姆定律计算电流表A的示数。
【解答】解:由电路图可知,R1与R2并联,电流表A测干路电流,电流表A1测R1支路的电流。
(1)并联电路各支路两端电压相等,都等于电源电压,
由欧姆定律可得电源电压:U=I1R1=0.6A×20Ω=12V;
(2)并联电路干路电流等于各支路电流之和,根据欧姆定律可得电流表A的示数:I=I1+I2=I1=0.6A+=0.9A。
答:(1)电源电压为12V;
(2)电流表A的示数为0.9A。
20.(1)深度表在水面上时,电路中的电流约为0.1A;
(2)电压表示数为2V时,潜水员下潜的深度为10m;
(3)在保证电路安全的情况下,该深度表能浸入水中的最大深度为40m。
【分析】(1)由图乙可知,该电路为R0和RP的串联电路,电压表测R0两端的电压,深度表在海面上深度为0m时,由图丙可知,此时RP阻值,由串联电路的电阻特点和欧姆定律可知电路中的电流;
(2)已知电压表示数为2V时,由欧姆定律可得通过R0的电流,由串联电路的电流特点和电压特点可知RP两端的电压,再求此时RP的阻值,对照图丙可知此时潜水员下潜的深度为;
(3)当电路中电流最大时,R0两端的电压最大为电压表量程的最大值,可得电路中最大电流且小于0.24A,由欧姆定律算出此时电路总电阻,由串联电路的电阻特点可知压敏电阻RP的阻值,对照图丙可知,此时下潜的深度即为该深度表能测量的最大深度。
【解答】解:(1)由图乙可知,该电路为R0和RP的串联电路,电压表测R0两端的电压;
深度表在海面上时,即h=0m时,由图丙可知,此时RP=40Ω,
由串联电路的电阻特点和欧姆定律可知电路中的电流为:I===≈0.1A;
(2)已知电压表示数为2V时,即R0两端的电压为U0=2V,
通过R0的电流为I0===A,即电路中的电流为I′=I0=A,
由串联电路的电压特点可知RP两端的电压为:UP=U﹣U0=6V﹣2V=4V,
则此时RP的阻值为:RP′===30Ω,
由图丙可知,此时潜水员下潜的深度为h′=10m;
(3)当电路中电流最大时,由U=IR可知R0两端的电压最大,
由电压表量程可知R0两端的电压最大为:U0大=3V,
由此可知电路中电流最大为:I大===0.2A<0.24A,
为保护电路,电路中允许通过的最大电流为0.2A,
此时电路总电阻为:R总===30Ω,
由串联电路的电阻特点可知压敏电阻RP的阻值为:RP=R总﹣R0=30Ω﹣15Ω=15Ω,
由图丙可知,此时下潜的深度为40m,即该深度表能测量的最大深度为40m。
答:(1)深度表在水面上时,电路中的电流约为0.1A;
(2)电压表示数为2V时,潜水员下潜的深度为10m;
(3)在保证电路安全的情况下,该深度表能浸入水中的最大深度为40m。
【计算4 欧姆定律与浮力杠杆的综合计算】
21.(1)定值电阻R0的阻值为10Ω;
(2)当平板空载时,电压表的示数为4V;
(3)如果只水平调节杠杆上触点B的位置,则触点B应向右移动,移动3cm。
【分析】(1)压力传感器和定值电阻串联接入电路,电压表测定值电阻两端的电压,由表格可知当平板空载时压力传感器的阻值,根据串联电路电压规律和电流特点,结合欧姆定律计算定值电阻R0的阻值;
(2)平板上物体对平板的压力等于自身的重力,根据杠杆平衡条件可得杠杆B点受到的压力,由力的作用是相互的可知压力传感器受到的压力,由表格可知此时压敏电阻的阻值,根据串联电路电阻规律结合欧姆定律计算此时通过电路的电流,进一步计算此时电压表的示数;
(3)电池组用久后电压变小,电路中电流变小,要增大电路中电流,需减小压力传感器的电阻,就要增大压力传感器受到的压力,其它条件不变,由杠杆平衡条件可知,需向右调节B触点,设调节距离为L,此时压力传感器阻值为R′′,利用欧姆定律求其大小;从图象可知传感器受到的压力,由于力的作用是相互的,可求杠杆A点受到的压力,利用杠杆平衡条件求L的大小。
【解答】解:(1)压力传感器和定值电阻串联接入电路,电压表测定值电阻两端的电压,
由表格可知当平板空载时,压力传感器的阻值为70Ω,
因串联电路总电压等于各部分电压之和,串联电路各处电流相等,
则由欧姆定律可得:=,即=,
解得:R0=10Ω;
(2)平板上物体对平板的压力:FB=G=120N,
由题知,AB:OB=5:1,则OA:OB=6:1,
由杠杆平衡条件FA×OA=FB×OB得杠杆A点受到的压力:FA=FB=×120N=20N,
由于力的作用是相互的,压力传感器受到的压力为20N,
由表格可知压敏电阻的阻值:R′=20Ω,串联电路总电阻等于各分电阻之和,
由欧姆定律得:I====0.4A,
此时电压表的示数;U0′=IR0=0.4A×10Ω=4V;
(3)电源用久后电压变小,电路中电流变小,若要求此时平板上重为120N的物体对应的电压表示数和电源电压为12V的情况下相同,则需减小压力传感器的电阻,就要增大压力传感器受到的压力,其它条件不变,由杠杆平衡条件可知,需向右移动B触点,设调节距离为L,此时压力传感器阻值为R′′,
因为此时电压表示数和R0的阻值不变,所以由欧姆定律可知电路中电流不变,仍然为0.4A,
则此时的电源电压:U1=IR总′=I(R′′+R0),
即9V=0.4A×(R′′+10Ω),
解得R′′=12.5Ω,
由表格可知可知传感器受到的压力为23N,
由于力的作用是相互的,杠杆A点受到的压力为:FA′=23N,
由杠杆平衡条件可得:
FA′×OA=FB×(OB+L),
23N×1.2m=120N×(×1.2m+L),解得:L=0.03m=3cm。
答:(1)定值电阻R0的阻值为10Ω;
(2)当平板空载时,电压表的示数为4V;
(3)如果只水平调节杠杆上触点B的位置,则触点B应向右移动,移动3cm。
22.(1)电源电压为6V,物体M所受的重力为22.5N;
(2)当物体M完全浸没时所受的浮力为7.5N;
(3)物体M的密度是3×103kg/m3。
【分析】(1)由图甲可知:电阻R0与滑动变阻器R串联,电压表测量滑动变阻器R两端的电压,电流表测量电路中电流;
由图丙读出电压表示数,根据欧姆定律和串联电路的特点求出电源电压;
根据欧姆定律求出变阻器接入电路的阻值,根据图乙得到拉力;
结合图丙分析得出具体的物理过程,深度为0~h1时,物体M不受浮力,此时拉力等于重力;
(2)深度大于h2时,物体M浸没在水中,拉力最小;由图丙读出水面深度为h2时电压表的示数,根据欧姆定律和串联电路的特点求出变阻器接入电路的阻值,根据图乙得到拉力;根据称重法测浮力公式可得物体M浸没在水中时所受的浮力;
(3)利用F浮=ρ水gV排可得物体M的体积,最后利用密度公式可求出物体M的密度。
【解答】解:(1)由电路图可知,R0与R串联,电压表测R两端的电压,电流表测电路中的电流;
当水面深度到达h1时,由图丙可知,电压表的示数U1=2V,
根据欧姆定律和串联电路的特点可得电源电压:
U=U0+U1=I1R0+U1=0.4A×10Ω+2V=6V;
根据I=可得变阻器接入电路的阻值为:
R1===5Ω,
由图乙可知,此时拉力F1=22.5N,
由于是往容器中缓慢注水,结合图丙可知:
当容器内水的深度在0~h1时,物体M没有浸在水中,不受浮力,此时弹簧的拉力与重力平衡,拉力最大;当容器内水的深度在h1~h2时,物体M浸在水中受浮力的作用,水的深度增加,浮力增大,拉力减小;当容器内水的深度大于h2时,物体M浸没在水中,浮力最大且不变,此时拉力最小。
结合上述分析可知:物体M所受的重力G=F1=22.5N,
(2)当水面深度到达h2时,由图丙可知,电压表的示数U2=4V,
因串联电路中总电压等于各分电压之和,
R0两端的电压:U0′=U﹣U2=6V﹣4V=2V,
电路中的电流:I2===0.2A,
根据I=可得变阻器接入电路的阻值为:
R2===20Ω,
由图乙可知,物体M浸没在水中时拉力为F2=15N;
根据称重法测浮力可知,物体M浸没在水中时受到的浮力:
F浮=G﹣F2=22.5N﹣15N=7.5N;
(3)根据F浮=ρ水gV排可得物体M的体积:
V=V排===7.5×10﹣4m3;
物体M的密度:ρ====3×103kg/m3。
答:(1)电源电压为6V,物体M所受的重力为22.5N;
(2)当物体M完全浸没时所受的浮力为7.5N;
(3)物体M的密度是3×103kg/m3。
23.(1)汽车入水前电路中的电流为0.075A;
(2)汽车受到的重力为1.8×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
【分析】(1)汽车入水前,R1表面水的压力为0,由图丙可知此时其阻值为20Ω,由乙图知R1和R2组成串联电路,电压表测的是R2两端的电压,示数为3V,已知总电压,根据串联电路的电压规律求出R1两端的电压,利用欧姆定律求出汽车入水前电路中的电流I;
(2)根据水池的水位比汽车入水前上升的高度,求出汽车排开水的体积,利用阿基米德原理求出汽车受到的浮力,根据汽车漂浮时,受到的重力和浮力平衡,大小相等,可求汽车受到的重力;
(3)先利用(1)中信息求出电阻R2的阻值,根据题中信息:汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于3V,即R1两端的电压为3V时,气囊充气打开,求出此时R2两端的电压,利用欧姆定律求出电路中的电流I′,利用欧姆定律求出电阻R1的阻值,由图丙可知,此时R1表面水的压力,即汽车底部A处受到水的压力,利用p=求出汽车A处受到水的压强,利用p=ρgh求出汽车A处浸入水中的深度。
【解答】解:(1)汽车入水前R1表面受到水的压力为0,由图丙可知此时R1的阻值为20Ω,由乙图可知R1和R2串联,电压表测R2两端的电压,示数为3V,根据串联电路的电压规律可知R1两端的电压为:
U1=U﹣U2=4.5V﹣3V=1.5V,
电路中的电流为:;
(2)当汽车漂浮时,水池的水位比汽车入水前上升了9cm,水池内水上升的体积即为汽车排开水的体积,则汽车排开水的体积为:
V排=S水池Δh=20m2×9×10﹣2m=1.8m3,
根据阿基米德原理可知:汽车受到的浮力为:
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1.8m3=1.8×104N,
当汽车漂浮时,汽车受重力和浮力,这两个力是一对平衡力,大小相等,则汽车受到的重力为:
G=F浮=1.8×104N;
(3)汽车入水前,电压表的示数为3V时,
则电阻R2的阻值为:
,
汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于3V,即此时R1两端的电压为3V,气囊充气打开,此时R2两端的电压为:
U2′=U﹣U1′=4.5V﹣3V=1.5V,
电路中的电流为:
I'===0.0375A,
电阻R1的阻值为:,
由图丙可知,此时R1表面水的压力为15N,即汽车底部A处受到水的压力为15N,汽车A处受到水的压强为:
汽车A浸入水中的深度为:
。
答:(1)汽车入水前电路中的电流为0.075A;
(2)汽车受到的重力为1.8×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
24.(1)当水深H=5cm时,水对容器底的压强为500Pa;
(2)木块A的重力5N;
(3)图中对应H0的值为28cm。
【分析】(1)已知水的密度和水的深度,根据p=ρgH算出当水深H=5cm时,水对容器底的压强;
(2)分析图2可知,当水深超过5cm时,电压表开始有示数,表明此时木块A刚好开始离开容器底,处于漂浮状态,根据漂浮条件G=F浮=ρ水gSH可求出木块A的重力;
(3)根据图丙可知,当R1两端的电压分别为1.5V、3.0V时R1消耗的电功率,根据I=分别求出电路中的电流,再根据串联电路的电压规律和欧姆定律分别列出电源电压的表达式,联立方程组求出电源电压、R2的阻值,当水深为10cm时根据欧姆定律求出此时R1的阻值,求出滑片上移的距离,进而求出滑动变阻器每1cm的电阻为1Ω,由图2可知,当水位到达H0后,电压表示数不再增加,表明此时滑片处于最上端即最大阻值处,根据图丙确定此时变阻器消耗的电功率,根据P2=I2R大求出滑动变阻器的最大阻值,求出对应的电阻丝的长度,由图丙可知,当水位在10~13cm时,电压表示数不变,表明接入电阻不变,求出短路部分的长度,即可解答。
【解答】解:(1)根据液体压强公式p=ρgh可得当水深H=5cm时,水对容器底的压强为:p=ρ水gH=1.0×103kg/m3×10N/kg×5×10﹣2m=500Pa;
(2)根据图丙可知,当水深超过5cm时,电压表开始有示数,表明此时木块A刚好开始离开容器底,处于漂浮状态,
根据物体沉浮条件可知木块A的重力为:G=F浮=ρ水gV排=ρ水gHS=1.0×103kg/m3×10N/kg×5×10﹣2m×0.01m2=5N;
(3)由图丙可知,当R1两端电压U1=1.5V时,功率为P1=1.125W,由P=UI可知此时电路中的电流为:I1===0.75A,
则电源电压为:U=U1+I1R2=1.5V+0.75A×R2……①,
当R1两端电压U2=3.0V时,功率为P2=1.8W,由P=UI可知此时的电流为:I2===0.6A,
则电源电压为:U=U2+I2R2=3.0V+0.6A×R2……②,
联立①②可得:U=9V,R2=10Ω,
当水深为10cm时,R1接入的电阻为:R1===5Ω,
此时滑片向上移动的距离为:d=10cm﹣5cm=5cm,
则滑动变阻器每1cm的电阻为1Ω;
当水位到达H0后,电压表示数不再增加,表明此时滑片处于最上端即最大阻值处,此时的R1的功率也为1.8W,则:
P2=I2R大=R大=R大=1.8W,
解方程可得:R大=5Ω或20Ω,
因为当水深为10cm时,R1接入的电阻为5Ω,则滑动变阻器最大阻值应为20Ω,
对应的电阻丝的长度为:L=1cm/Ω×20Ω=20cm,
由图丙可知,当水位在10~13cm时,电压表示数不变,表明接入电阻不变,
即短路部分的长度为:l=13cm﹣10cm=3cm,
所以图丙中对应H0的值为:H0=H+L+l=5cm+20cm+3cm=28cm。
答:(1)当水深H=5cm时,水对容器底的压强为500Pa;
(2)木块A的重力5N;
(3)图甲和乙中对应H0的值为28cm。
25.(1)当物体AB底面朝下放置在水平桌面上,对桌面产生的压强大小为5×103Pa;
(2)当物体AB上表面与水面相平时,物体AB受到的浮力大小30N;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,滑动变阻器R连入电路的阻值大小10Ω;
(4)当水面从物体AB上表面逐渐下降至下表面刚好离开水面的过程中,弹簧伸长了15cm。
【分析】(1)根据压力F=G和p=计算压强
(2)物体浸没时,V排=V物,根据阿基米德原理F浮=ρ液gV排可求浮力大小;
(3)根据串联电压特点计算定值电阻的电压,根据串联电压之比等于电阻之比确定滑动变阻器的电阻;
(4)利用图像可求力与伸长量的比值,再由弹簧弹力的变化可求弹簧的伸长量。
【解答】解:(1)当物体AB底面朝下放置在水平桌面上,F=G=50N,
压强p===5×103Pa;
(2)当物体AB上表面与水面相平时,物体AB刚好浸没水中V排=V物=Sh=0.01m2×0.3m=3×10﹣3m3;
物体AB所受浮力F浮=G排=ρ水gV排=1.0×103kg/m3×10N/kg×3×10﹣3m3=30N;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,R0的电压U0=U﹣UP=3V﹣1.5V=1.5V;
根据串联电路的电压之比等于电阻之比,两者电压相等,则电阻相等,因而R=R0=10Ω。
(4)水面与物体AB上表面相平时,弹簧对物体AB的拉力F弹=G物﹣F浮=50N﹣30N=20N;
水面下降至与物体AB下表面相平时,弹簧对物体AB的拉力F弹′=G物=50N;
水面从物体AB上表面逐渐下降至与下表面相平过程中,弹簧拉力的变化量ΔF弹=F弹'﹣F弹=50N﹣20N=30N;
由乙图可知:==2N/cm;
物体AB刚好离开水面时,弹簧伸长的长度ΔL′==15cm。
答:(1)当物体AB底面朝下放置在水平桌面上,对桌面产生的压强大小为5×103Pa;
(2)当物体AB上表面与水面相平时,物体AB受到的浮力大小30N;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,滑动变阻器R连入电路的阻值大小10Ω;
(4)当水面从物体AB上表面逐渐下降至下表面刚好离开水面的过程中,弹簧伸长了15cm。
26.(1)此时滑动变阻器R2接入电路中的阻值为20Ω;
(2)R2的滑片在位置M时,该液体密度计的“0”刻度线与电压表表盘1伏的刻度线相对应;
(3)该液体密度计的最大测量值为2.1g/cm3。
【分析】(1)由图可知,R0、R1和滑动变阻器R2串联,根据串联电路特点、欧姆定律计算出电路电流;
根据欧姆定律计算电路总电阻;
已知桶重和水重,要加班计算压敏电阻此时所受到的压力,由表格得出此时压敏电阻的阻值,根据串联电路电阻规律即可求出滑动变阻器接入电路中的阻值;
(2)不装液体时,密度计示数为0,由表格得出此时R1的阻值,根据串联电路的特点和欧姆定律计算出此时电压表的示数;
(3)根据表格数据可知压力越大时R1的阻值越小,所以据此可知当R2滑片在左端时R1的阻值最小,受到的压力最大;根据欧姆定律求出当电压表指针满偏时电路中的电流和此时电路中的总电阻以及R1的阻值最小值;根据图表可得R1与F之间的关系式,据此求出此时压敏电阻受到的最大压力,最后根据重力公式和密度公式计算出能够测量的最大密度。
【解答】解:(1)由图可知,R0、R1和滑动变阻器R2串联,电压表测量R0两端电压,已知在桶内注满水,闭合S,电压表的示数为1.5V,
串联电路各处电流相等,根据欧姆定律可得电路电流为:I=I0===0.15A,
根据欧姆定律可得此时总电阻为:R===80Ω;
此时压敏电阻受到的压力为:F=G水+G桶=1N+1N=2N,
由表格数据可知:F=2N时,R1=50Ω,
则根据串联电路的总电阻等于各分电阻之和可得,R2的电阻为:R2=R﹣R1﹣R0=80Ω﹣50Ω﹣10Ω=20Ω;
(2)该液体密度计的“0”刻线,即桶内不装液体时电压表的示数,由于当桶内不装液体时,压敏电阻受到的压力为空桶重力:F0=G桶=1N,
由表格数据可得:F0=1N时,R1′=90Ω,
根据串联电路的总电阻等于各分电阻之和可得:R′=R1′+R0+R2=90Ω+10Ω+20Ω=120Ω;
根据欧姆定律可得此时电压表示数为:U0′=×R0=×10Ω=1V,
即该液体密度计的“0”刻度线与电压表表盘1伏的刻度线相对应;
(3)当R滑全部接入时,滑动变阻器最大值为:R2大=24Ω,根据电压表的量程可知:U0大=3V,
根据欧姆定律可得此时电路中电流为:I1===0.3A,
根据欧姆定律可得此时总电阻为:R小===40Ω,
根据串联电路的总电阻等于各分电阻之和可得此时R1的电阻为:R1小=R小﹣R0﹣R2大=40Ω﹣10Ω﹣24Ω=6Ω,
根据图表可得R1与FB之间的关系式为:R1=130Ω﹣40Ω/N×F,
则此时压敏电阻受到的压力为:F大===3.1N,
则此时桶中液体的重力为:G液大=FA大﹣G桶=3.1N﹣1N=2.1N,
液体的质量为:m液大===0.21kg=210g,
则液体的密度为:ρ液大===2.1g/cm3。
答:(1)此时滑动变阻器R2接入电路中的阻值为20Ω;
(2)R2的滑片在位置M时,该液体密度计的“0”刻度线与电压表表盘1伏的刻度线相对应;
(3)该液体密度计的最大测量值为2.1g/cm3。
27.(1)当该电子秤恰好报警时,托盘所放物体的质量为30kg;
(2)托盘的支撑点B应向右移,移动的距离为8cm。
【分析】(1)闭合开关,两电阻串联接入电路,电压表测定值电阻两端的电压,
当电压表的示数等于或大于3V时,电子秤会自动发出报警声,根据欧姆定律计算此时通过电路的电流,根据串联电路电压规律计算此时力敏电阻两端的电压,根据欧姆定律计算此时力敏电阻接入电路的阻值,由表格可知力敏电阻受到的压力,
根据杠杆平衡条件可得F×OA=G×OB,据此计算托盘则物体是重力,根据m=计算托盘所放物体的质量;
(2)根据G=mg计算托盘上所放物体的重力,根据杠杆平衡条件可得F×OA=G′×OB′,进一步计算OB′,据此确定B点移动的方向,进一步计算托盘的支撑点B移动的距离。
【解答】解:(1)闭合开关,两电阻串联接入电路,电压表测定值电阻两端的电压,
当电压表的示数等于或大于3V时,电子秤会自动发出报警声,根据欧姆定律可得此时通过电路的电流I===0.5A,
串联电路总电压等于各部分电压之和,此时力敏电阻两端的电压U1=U﹣U2=15V﹣3V=12V,
此时力敏电阻接入电路的阻值R2===24Ω,
由表格可知力敏电阻受到的压力为150N,
根据杠杆平衡条件可得F×OA=G×OB,则托盘则物体是重力G==2F=2×150N=300N,
托盘所放物体的质量m===30kg;
(2)托盘上所放物体的重力G′=m′g=50kg×10N/kg=500N,
根据杠杆平衡条件可得F×OA=G′×OB′,则OB′===12cm,
则托盘的支撑点B应向右移×40cm﹣12cm=8cm。
答:(1)当该电子秤恰好报警时,托盘所放物体的质量为30kg;
(2)托盘的支撑点B应向右移,移动的距离为8cm。
28.(1)物体A的重力为80N;
(2)停止加水后物体A所受的浮力为20N;
(3)停止加水后物体A底部所受液体压强为500Pa;
(4)停止加水后容器底部所受液体压强为2500Pa。
【分析】(1)R1为竖直固定的光滑均匀金属棒,总电阻为20Ω,总长度为40cm,当弹簧下端不挂物体时,滑片P位于R1的最上端,当弹簧下端挂边长为20cm的立方体A时,滑片P位于R1的最下端,据此分析弹簧的形变量为40cm,由乙可知弹簧受到的拉力,物体A的重力等于弹簧受到的拉力;
(2)闭合开关,两电阻串联接入电路,电压表测滑片以上部分电阻两端的电压,根据串联电路电阻规律结合欧姆定律计算通过电路的电流,根据串联电路电流特点结合欧姆定律计算滑片以下部分的电阻,进一步计算滑片移动的距离和弹簧的形变量,由乙可知弹簧受到的拉力,
物体受到的浮力等于物体的重力与弹簧受到的拉力之差;
(3)根据阿基米德原理计算物体浸入水中的体积,根据体积公式计算物体浸入水中的深度,根据压强公式计算停止加水后物体A底部所受液体压强;
(4)滑片P位于R1的最下端时物体A的下端距容器底的距离h=10cm=0.1m,根据压强公式计算停止加水后容器底部所受液体压强。
【解答】解:(1)R1为竖直固定的光滑均匀金属棒,总电阻为20Ω,总长度为40cm,当弹簧下端不挂物体时,滑片P位于R1的最上端,当弹簧下端挂边长为20cm的立方体A时,滑片P位于R1的最下端,即弹簧的形变量为40cm,由乙可知弹簧受到的拉力为80N,则物体A的重力G=80N;
(2)闭合开关,两电阻串联接入电路,电压表测滑片以上部分电阻两端的电压,
串联电路总电阻等于各部分电阻之和,根据欧姆定律可得通过电路的电流:I===0.5A,
串联电路各处电流相等,滑片以下部分的电阻:RP===15Ω,
则滑片移动的距离为hP=×40cm=10cm,
弹簧的形变量为40cm﹣10cm=30cm,由乙可知弹簧受到的拉力为60N,
则物体受到的浮力为F浮=G﹣F=80N﹣60N=20N;
(3)物体浸入水中的体积:V排===2×10﹣3m3,
物体浸入水中的深度:h′===0.05m,
停止加水后物体A底部所受液体压强:p=ρ水gh′=1.0×103kg/m3×10N/kg×0.05m=500Pa;
(4)滑片P位于R1的最下端时物体A的下端距容器底的距离h=10cm=0.1m,
停止加水后容器底部所受液体压强:p′=ρ水g(h+hP+h′)=1.0×103kg/m3×10N/kg×(0.1m+0.1m+0.05m)=2500Pa。
答:(1)物体A的重力为80N;
(2)停止加水后物体A所受的浮力为20N;
(3)停止加水后物体A底部所受液体压强为500Pa;
(4)停止加水后容器底部所受液体压强为2500Pa。
29.(1)放入物体M前,电流表的示数为0.2A;
(2)M漂浮在水中时所受到的浮力为12N;
(3)当电流表的示数为0.3A时,物体M相对于漂浮在水中时移动的距离为1cm。
【分析】(1)通过图像得出放入物体前的电阻值,应用欧姆定律计算电流值。
(2)应用阿基米德原理计算浮力。
(3)应用图像欧姆定律及体积关系求浸没深度。
【解答】解:(1)放入物体M前,水的深度h1=12cm,根据图像可知当h1=12cm时,电阻R=60Ω,
则电流表示数为:I=;
(2)M漂浮在水中时浸入水中的深度为6cm,排开水的体积V排=SMh浸=200cm2×6cm=1200cm3,
根据阿基米德原理可得M漂浮在水中时所受到的浮力:
N/kg×1200×10﹣6m3=12N;
(3)当M放入水中漂浮时,水面上升的高度Δh==,
则M放入水中漂浮时,水箱中水的深度h2=h1+△h=12cm+4cm=16cm;
当电流为0.3A时,根据欧姆定律R=,由图像可知此时水的深度h3=18cm,
当电流表的示数为0.3A时,与M漂浮相比,水面上升的高度△h′=h3﹣h2=18cm﹣16cm=2cm,
因水面上升,所以物体M应下压,
根据ΔV排的两种计算方法可得:ΔV排=S容△h′=SM(△h′+h下压),
则物体M相对于漂浮在水中时向下移动的距离:
h下压===1cm。
答:(1)放入物体M前,电流表的示数为0.2A;
(2)M漂浮在水中时所受到的浮力为12N;
(3)当电流表的示数为0.3A时,物体M相对于漂浮在水中时移动的距离为1cm。
30.(1)未放入物体时,水对容器底的压强为900Pa;
(2)R2的阻值为10Ω:
(3)物体A的密度为0.6×103kg/m3。
【分析】(1)知道未放入物体时水的深度,利用p=ρgh求出水对容器底的压强;
(2)由电流先增大后减小可知,当GA=F浮时,杆子受到的力F=0,由图乙可知,此时R1=10Ω,由图甲可知,R1、R2串联,根据欧姆定律可知此时的电流最大,利用串联电路特点和欧姆定律求出R2的阻值;
(3)还未进入水中时,A的重力等于杆子的受到的力,此时I0=0.2A,根据欧姆定律和电阻串联的特点得出此时R1的阻值,由图乙可知,根据GA=F得出此时A的重力;
当I1=0.4A时,根据欧姆定律和电阻串联的特点得出此时R1的阻值,由图乙可知,此时杆子受到的力F1;
分此时杆给的力F1为向下或向上的拉力两种情况,对物体受力分析,结合阿基米德原理得出A的体积,进而得出物体和水的总体积,结合题意确定A的体积,利用密度公式得出物体A的密度。
【解答】解:(1)未放入物体时,水深为9cm,水对容器底的压强为:;
(2)由电流先增大后减小可知,当GA=F浮时,杆子受到的力F=0,由图乙可知,此时R1的阻值最小为10Ω,
由图甲可知,R1、R2串联,根据欧姆定律可知,此时电路中的电流最大:I2=0.5A,
由I=可知,R1、R2的总阻值:R===20Ω,
根据串联电路特点可知,R2的阻值:R2=R﹣R1=20Ω﹣10Ω=10Ω;
(3)还未进入水中时,A的重力等于杆子的受到的力,此时I0=0.2A,此时R1的阻值为,
由图乙可知,此时A的重力为GA=F=1.2N,
当I1=0.4A时,此时R1的阻值为,
由图乙可知,此时杆子受到的力为F1=0.2N,
若此时杆给的力F1为向下的拉力,则物体的重力和拉力之和等于浮力,即,
则A的体积为,
物体和水的总体积为,
依题意,
因为640cm3>600cm3,所以A的体积不为280cm3。
若此时杆给的力F1为向上的压力,则物体的重力等于压力与浮力之和,即,
则A的体积为,
物体和水的总体积为,
依题意,因为560cm3<600cm3,所以A的体积为,
物体A的密度为。
答:(1)未放入物体时,水对容器底的压强为900Pa;
(2)R2的阻值为10Ω:
(3)物体A的密度为0.6×103kg/m3。
31.(1)弹簧恰好处于自然状态,此时通过仪器A的电流为0.15A;
(2)若仪器A示数为0.2A时,物体排开水的体积V排为550cm3;
(3)仪器A示数为0.2A时,水槽中水的总质量为3125g。
【分析】(1)弹簧恰好处于自然状态,此时弹簧不受力,所以压杆没有压力,由乙图可知压力传感器的电阻,根据欧姆定律计算此时通过仪器A的电流;
(2)根据欧姆定律计算仪器A示数为0.2A时压力传感器的电阻,
由图可知此时压杆压力,根据杠杆平衡条件计算B处的拉力,根据重力公式计算物体的重力,根据称重法计算物体所受浮力,根据阿基米德原理计算物体排开水的体积;
(3)弹簧每受到1N的力时长度变化0.5cm,据此计算此时弹簧的伸长量,弹簧恰好处于自然状态时长度为10cm,弹簧每受到1N的力时长度变化0.5cm,物体的重力为6N,进一步计算挂上物体后的伸长量,据此计算加水后物体底面上升的高度,
由(2)得物体排开水的体积,根据体积公式计算物体浸入水的高度,根据体积公式计算水槽内水的体积,根据m=ρV计算水槽中水的总质量。
【解答】解:(1)弹簧恰好处于自然状态,此时弹簧不受力,所以压杆没有压力,由乙图可知压力传感器的电阻为40Ω,
由欧姆定律可得此时通过仪器A的电流为:I===0.15A;
(2)仪器A示数为0.2A时,压力传感器的电阻为:R1===30Ω,
由图可知,此时压杆压力为1N,根据杠杆平衡条件可知F×OA=F拉×OB,则F拉==1N×=0.5N,
物体的重力为:G=mg=0.6kg×10N/kg=6N,
所以物体所受浮力为F浮=G﹣F拉=6N﹣0.5N=5.5N,
物体排开水的体积为:V排===5.5×10﹣4m3=550cm3;
(3)弹簧每受到1N的力时长度变化0.5cm,所以此时弹簧的伸长量为Δl1=0.5N×0.5cm/N=0.25cm,
弹簧恰好处于自然状态时长度为10cm,弹簧每受到1N的力时长度变化0.5cm,物体的重力为6N,挂上物体后的伸长量为Δl2=6N×0.5cm/N=3cm,
所以加水后物体底面上升的高度为Δl=Δl2﹣Δl1=3cm﹣0.25cm=2.75cm,
由(2)得物体排开水的体积为550cm3,所以物体浸入水的高度为h1===5.5cm,
水槽内水的体积为:V=S(h+Δl)+(S﹣S正方体)h1=300cm2×(4cm+2.75cm)+(300cm2﹣10cm×10cm)×5.5cm=3125cm3,
水槽中水的总质量为:m=ρV=1g/cm3×3125cm3=3125g。
答:(1)弹簧恰好处于自然状态,此时通过仪器A的电流为0.15A;
(2)若仪器A示数为0.2A时,物体排开水的体积V排为550cm3;
(3)仪器A示数为0.2A时,水槽中水的总质量为3125g。
32.(1)汽车入水前电路中R1的电流为0.1A;
(2)汽车受到的重力2.5×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
【分析】(1)汽车入水前,R1表面受到水的压力为0,由图丙可知此时其阻值为20Ω,由乙图知R1和R2组成串联电路,电压表测的是R2两端的电压,示数为4V,已知总电压,根据串联电路的电压规律求出R1两端的电压,利用欧姆定律求出汽车入水前电路中的电流I;
(2)根据水池的水位比汽车入水前上升的高度,求出汽车排开水的体积,利用阿基米德原理求出汽车受到的浮力;
(3)先利用(1)中信息求出电阻R2的阻值,根据题中信息:汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于4V,即R1两端的电压为4V时,气囊充气打开,求出此时R2两端的电压,利用欧姆定律求出电路中的电流I′,利用欧姆定律求出电阻R1的阻值,由图丙可知,此时R1表面水的压力,即汽车底部A处受到水的压力,根据p=得出此时压敏电阻所受的压强,根据hA=得出气囊充气打开时汽车A处浸入水中的深度。
【解答】解:(1)汽车入水前,R1表面受到水的压力为0,由图丙可知此时其阻值为20Ω,由乙图知R1和R2组成串联电路,电压表测的是R2两端的电压,示数为4V,
根据串联电路的电压规律U=U1+U2得,R1两端的电压为:U1=U﹣U2=6V﹣4V=2V,
电路中的电流为:I===0.1A;
(2)当汽车漂浮时,水池的水位比汽车入水前上升了10cm,
则汽车排开水的体积为:V排=S水池Δh=25m2×10×10﹣2m=2.5m3,
汽车受到的浮力为:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×2.5m3=2.5×104N,
汽车漂浮时,汽车受到的重力等于浮力,所以汽车受到的重力为2.5×104N;
(3)汽车入水前,电压表的示数为4V时,电阻R2的阻值为:R2===40Ω,
汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于4V即R1两端的电压为4V时,气囊充气打开,
此时R2两端的电压为:U2′=U﹣U1′=6V﹣4V=2V,
电路中的电流为:I′===0.05A,
电阻R1的阻值为:R1′===80Ω,
由图丙可知,此时R1表面受到水的压力为15N,即汽车底部A处受到水的压力为15N,
此时A处所受水的压强为p===104Pa,
汽车A处浸入水中的深度为hA===1m。
答:(1)汽车入水前电路中R1的电流为0.1A;
(2)汽车受到的重力2.5×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
专题05电路初探与欧姆定律(实验专题训练)
【计算1并联电路的电流规律】
1.如图甲所示,当开关S闭合时,两个电流表A1、A2的示数分别如图乙所示,问:
(1)电流表A1、A2使用的量程和读数分别是多少?
(2)通过灯泡L1、L2的电流分别是多少?
2.如图所示,在探究“并联电路的电流规律”时,闭合开关S后,电流表A2的示数是0.7A,电流表A的示数如图2。求:
(1)A的示数为多少A?
(2)电流表A1的示数是多少A?
3.如图甲所示的电路,当开关闭合后,电流表A1的示数如图乙所示,电流表A2的示数如图丙所示。求:通过小灯泡L1和L2的电流大小。
4.在如图所示的电路中,开关闭合后电流表A1的示数为1.8A,电流表A2的示数为0.7A。求:通过灯泡L1的电流I1和通过灯泡L2的电流I2。
5.如图甲所示,当开关S1闭合,S2和S3都断开时,电流表A1的示数如图乙所示,求:
(1)电流表A2和A的示数;
(2)当开关S2和S3闭合,S1断开时,电流表A和A2的示数分别为0.7A和0.3A,电流表A1的示数;
(3)若将S1、S2和S3同时闭合会发生什么现象?
【计算2 串联电路的电压规律】
6.如图甲所示,V1、V2是两只相同的电压表。当闭合开关S后,灯泡L1和L2正常都发光,此时两只电压表的指针偏转角度相同,如图乙所示。
(1)求灯泡L1和L2两端的电压;
(2)若将灯泡L1和L2改接为图丙所示的电路,电源电压不变,闭合开关后灯泡L1和L2都发光,此时电流表A2的示数为1.5A,电流表A1的示数为1.2A求此时通过灯泡L2的电流和灯泡L2两端的电压。
7.(1)在图甲所示的电路中,当开关S1、S2都闭合时,电流表的示数为0.58A;当开关S1断开、S2闭合时,电流表的示数为0.22A。请计算当开关S1、S2都闭合时通过电灯L1的电流。
(2)如图乙所示的电路,当开关S闭合后,电压表V1、V2的示数分别为2.2V和5.8V。请计算当开关S闭合时电灯L2两端的电压。
8.如图所示得测量电路中,闭合开关后电压表V1的示数为2V,V2的示数4V,求:
(1)电压表V的示数是多少?
(2)此电源需要几个干电池串联而成?
9.如图甲所示的电路中,电源由三节新干电池串联组成。闭合开关后,两灯泡均发光,电流表的示数如图乙所示,电压表V2指针如图丙所示。试求:
(1)电源电压是多少?
(2)流过灯L1和L2的电流分别是多少?
(3)L1和L2两端的电压分别是多少?
【计算3 欧姆定律公式的应用】
10.如图所示,R1=30Ω,闭合开关,电压表和电流表的示数分别为6V和0.5A.求:
(1)通过电阻R1的电流;
(2)电阻R2的阻值。
11.如图所示电路中,电源电压恒为30V,电阻R1为15Ω,同时闭合开关S1、S2时,电流表的示数为2.5A。求:
(1)通过电阻R2的电流;
(2)电阻R2的阻值。
12.如图所示,电源电压为8伏且不变,闭合开关,电压表、电流表的示数分别为2伏和0.1安。求:
①电阻R1的阻值;
②电阻R2的阻值;
③试利用串联电路电流、电压的特点以及欧姆定律推导串联电路中电阻的特点:R=R1+R2。
13.如图所示,电源电压保持不变。当闭合开关S,滑动变阻器滑片P从a端移到b端,两电表示数变化关系用图乙中的线段AB表示。求:
(1)求滑动变阻器最大阻值。
(2)电源电压和R1的阻值。
(3)滑片P滑到ab中点时电压表的示数。
14.如图1所示的电路中,电源电压为14伏保持不变。滑动变阻器标有“20欧 2安”字样,闭合开关S,电流表A的示数如图2所示。
①求此时滑动变阻器R连入电路的阻值。
②移动变阻器滑片P可以使电流表的最大值和最小电流。
15.新冠肺炎疫情期间,体温检测成为社区、商场等公共场所一种重要的防控手段。如图甲为某电子测温仪的内部简化电路图,测温仪探头内有一热敏电阻Rt,其阻值随温度变化关系如图乙所示。R1为阻值可调的电阻箱,其最大电阻为300Ω,允许通过的最大电流为0.02A,电流表的量程0~0.6A,电压表的量程是0﹣3V,电源电压恒定。某次测试时,将电阻箱的阻值调为R,发现电流表示数为0.01A,此时Rt两端电压为4V。
(1)此时电路中Rt的电阻是多少?
(2)当电流表示数为0.01A时,环境温度是多少?
(3)当环境温度为30℃,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,求电源电压是多少?
(4)若温度为40℃,则电阻箱允许接入电路的阻值调节范围是多少?
16.实际上电源内部都有一定的电阻,如干电池,我们需要用电压U和电阻r两个物理量来描述它。实际计算过程中,可以把它看成是由一个电压为U、电阻为0的理想电源与一个电阻值为r的电阻串联而成,如图甲所示。在图乙中,R1=9Ω,滑动变阻器R2的最大值为20Ω,闭合开关S,滑动变阻器的滑片从a调节到b的过程中,电流表示数变化范围为0.1A~0.3A,把电源按图甲中的等效方法处理(忽略电流表内阻影响)。求:
(1)电源电压U和电阻r;
(2)当滑动变阻器的滑片处于中点时,电源内阻r的电压和电流。
17.在如图所示的电路中,电源电压为16V不变,滑动变阻器R2上标有“27Ω 2A”的字样,闭合开关S后,电流表的示数为1A,电压表的示数为5V求:
(1)电阻R1的阻值;
(2)电路中的最小电流;
(3)在电压表和电流表不改变量程的情况下,为使电路正常工作,滑动变阻器R2连入电路的阻值范围。
18.如图所示电路,电源电压恒定为3V,R2=10Ω,当S1闭合,S2、S3断开,电流表示数为0.6A。
求:(1)R1阻值为多少?
(2)当S2闭合,S1、S3断开时,电压表示数为多少?
(3)当S1、S3闭合,S2断开时,电流表示数为多少?
19.如图所示的电路中,电源电压不变,已知定值电阻R1=20Ω,R2=40Ω,开关闭合后,电流表A1的示数为0.6A。求:
(1)电源电压;
(2)电流表A的示数。
20.随着我国经济的发展,人民生活水平日益提高,我国出现了越来越多的潜水爱好者。为了保障安全,潜水员潜水时会佩戴如图甲所示的水压表和深度表。图乙是某深度表的工作原理简化电路图,电源电压U=6V且恒定不变,定值电阻R0=15Ω,电压表量程为0 3V,Rp是阻值随水深度变化的电阻,其变化关系图象如图丙所示,Rp允许通过的最大电流为0.24A。求:
(1)深度表在水面上时,电路中的电流(计算结果保留1位小数);
(2)电压表示数为2V时,潜水员下潜的深度;
(3)在保证电路安全的情况下,该深度表能浸入水中的最大深度。
【计算4 欧姆定律与浮力杠杆的综合计算】
21.某物理兴趣小组设计了一套测量货车重力的模拟装置,工作原理如图所示。ABO为一水平杠杆,OA长1.2m,O为支点,AB:OB=5:1,平板上物体所受重力大小通过电压表读数显示。压力传感器R固定放置,R的阻值随所受压力F变化的关系如表所示。当电源电压U为12V,平板空载时,闭合开关S,电压表的示数为1.5V。平板、压杆和杠杆的质量均忽略不计。
F/N 0 4 8 12 16 20 23 …
R/Ω 70 60 50 40 30 20 12.5 …
(1)定值电阻R0的阻值;
(2)当平板上物体重120N时,电压表的示数;
(3)电池组用久后电源电压变小为9V,要求平板上重为120N的物体对应的电压表读数和电池组的电压U=12V的情况下相同,其它条件不变,只水平调节杠杆上触点B的位置即可实现,试判断并计算触点B应向哪个方向移动?移动多少距离?
22.某物理兴趣小组利用下列装置来测量物体M的密度,其部分结构如图甲所示。电源电压恒定,R0为10Ω的定值电阻,滑动变阻器R的阻值随弹簧的拉力F变化关系如图乙,T为容器的阀门。现将物体M悬挂于P点放入容器中,保持静止状态,打开阀门T,随着水缓慢注入容器,电压表示数U随容器中水的深度h变化关系如图丙中的实线所示。当水面深度到达h1时,电流表示数为0.4A(弹簧电阻忽略不计,物体M不吸水),求:
(1)电源电压和物体M所受的重力;
(2)当物体M完全浸没时所受的浮力;
(3)物体M的密度。
23.如图甲所示,恩西同学设计了一个汽车落水安全装置并进行了试验,在汽车的四个门板外侧分别安装一个气囊,气囊的触发由图乙所示电路中a、b间的电压来控制,压敏电阻R1水平安装在汽车底部A处,R1的阻值随其表面水的压力的变化如图丙所示。某次试验时:汽车入水前把R2的滑片调到合适位置不动,闭合开关S,电压表的示数为3V,再把汽车吊入足够高的长方体水池中缓慢下沉,直到a、b间的电压等于或大于3V时,气囊就充气打开,使汽车漂浮在水中,试验装置相关参数如表所示。
电源电压 4.5V
R1接触水的面积 15cm2
长方体水池底面积 20m2
(1)求汽车入水前电路中的电流;
(2)当汽车漂浮时,测得水池的水位比汽车入水前上升了9cm(水未进入车内),求汽车受到的重力;
(3)求气囊充气打开时汽车A处浸入水中的深度。
24.某量水仪的内部简化结构如图甲所示,木块A(底面积为0.01m2)通过一轻质绝缘细杆与轻质滑片P固定在一起。在检测量水仪时,发现滑动变阻器有一段金属丝发生短路,滑动变阻器的电功率P、电压表示数U与水深H的关系分别如图乙和丙所示。已知电源电压U0恒定不变,R2为定值电阻,R1的阻值与金属丝长度成正比(g取10N/kg,容器足够高,不计绝缘细杆、滑片的体积和自重及滑片处的摩擦)。求:
(1)当水深H=5cm时,水对容器底的压强。
(2)木块A的重力。
(3)图乙、丙中对应H0的值。
25.海南水利资源丰富,小明设计了如图甲所示的水文站测量昌化江水位的原理图。电源电压U=3V,定值电阻R0=10Ω,滑动变阻器R长20cm,最大阻值20Ω。且滑动变阻器的阻值随滑片P从最上端C位置移动到最下端D位置的过程中均匀变化(滑片P移动过程中摩擦不计)。弹簧下端悬挂一重力为50N的物体AB,其底面积为0.01m2、长为0.3m。弹簧伸长量与它受到拉力的关系如图乙所示(不计弹簧质量,连接弹簧两端的绝缘细绳不可伸长)。已知闭合开关S后,当物体AB上表面与水面相平时,滑片P刚好在滑动变阻器R的最上端C位置。g取10N/kg,ρ水=1×103kg/m3。求:
(1)当物体AB底面朝下放置在水平桌面上,对桌面产生的压强大小;
(2)当物体AB上表面与水面相平时,物体AB受到的浮力大小;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,滑动变阻器R连入电路的阻值大小;
(4)当水面从物体AB上表面逐渐下降至下表面刚好离开水面的过程中,弹簧伸长了多少cm?
26.图所示是某校科技小组制作的液体密度计的工作原理图,其中空桶重1N,测量时需将桶内注满液体。电源电压恒为12V,定值电阻R0的阻值为10Ω;电压表的量程为0~3V,表盘改造后可直接显示所测液体的密度值;滑动变阻器R2标有“24Ω 0.5A”的字样,R1为压敏电阻,其阻值与所受压力F变化关系如表所示(R1的阻值不为0)。在桶内注满水时,桶内水重恰为1N,闭合开关S,移动R 的滑片至位置M时,电压表的示数为1.5V。
R1/Ω 130 110 90 70 50 30 ..
F/N 0 0.5 1.0 0.5 2.0 2.5
(1)此时滑动变阻器R2接入电路中的阻值为多大?
(2)R2的滑片在位置M时,该液体密度计的“0”刻度线与电压表表盘多少伏的刻度线相对应?
(3)移动R2的滑片可以改变密度计的最大测量值(此时电压表指针满偏)。已知桶的容积为100mL,则该液体密度计的最大测量值为多少?(g取10N/kg)
27.如图是电子秤的内部电路,杠杆ABO始终处于水平位置,B是杠杆的中点,电源电压恒为15V,R2是阻值为6Ω的定值电阻,R1是压敏电阻,它的阻值随压力变化关系如表,当电压表的示数等于或大于3V时,电子秤会自动发出报警声。(杠杆、支架及托盘的重均忽略不计)
压力F/N 50 100 150 200 250 300
阻值R1/Ω 50 30 24 20 17 16
(1)当该电子秤恰好报警时,托盘所放物体的质量为多少?
(2)已知杠杆OA的长为40cm,欲使在托盘上所放物体的质量为50kg才报警。则托盘的支撑点B应向左还是向右移?移动的距离为多少?
28.某款水位测量仪原理如图甲,电源电压恒为15V,R2是阻值为10Ω的定值电阻,R1为竖直固定的光滑均匀金属棒,总电阻为20Ω,总长度为40cm。滑片P一端与R1无摩擦良好接触,另一端固定在轻质弹簧下端,中间部分与可伸缩的轻质导线M相连,弹簧的伸长量与所受的拉力关系如图乙所示。某次测试时,当弹簧下端不挂物体时,滑片P位于R1的最上端,当弹簧下端挂边长为20cm的立方体A时,滑片P位于R1的最下端,此时物体A的下端距容器底的距离h=10cm,往容器中加水,物体A会上升,当电压表的示数为7.5V时停止加水,g=10N/kg。求:
(1)物体A的重力;
(2)停止加水后物体A所受的浮力;
(3)停止加水后物体A底部所受液体压强;
(4)停止加水后容器底部所受液体压强。
29.小明在实验室寻得一个压敏电阻R,他设计了如图甲所示的装置探究R的电阻值随液体深度的变化关系。电源电压恒为12V,在R表面涂上绝缘漆并将其紧密嵌在底面积为300cm2、高为20cm的柱形储水箱底部,R上表面直接与水接触。先在水箱中注入12cm深的水,然后在水中放入一底面积为200cm2、高为10cm的柱体M,通过上提和下压M来改变水的深度,当M竖直地漂浮在水面时浸入水中的深度为6cm。根据实验数据描绘出R的阻值随水深h的变化关系如图乙所示。求:
(1)放入物体M前,电流表的示数;
(2)M漂浮在水中时所受到的浮力;
(3)当电流表的示数为0.3A时,物体M相对于漂浮在水中时移动的距离。
30.一力敏电阻通过轻质细杆与圆柱形物体A连接,力敏电阻所在电路图如图甲虚线框所示,其中电源电压为10V。R2为定值电阻。研究所得力敏电阻R1的阻值与所受力大小之间的关系如图乙所示。现将物体A缓慢放入高15cm,底面积为40cm2的圆柱形容器中,容器内装有深度为9cm的水。还未进入水中时,电流表示数I0=0.2A。当物体A一半体积浸入液体中时,电流为I1=0.4A。在物体缓慢下降到完全浸没过程中,发现电流先增大后减小,且此过程中电流表最大示数为I2=0.5A(整个过程水未溢出,细杆足够长,g取10N/kg)。求:
(1)未放入物体时,水对容器底的压强;
(2)R2的阻值;
(3)物体A的密度。
31.真真同学设计了一款弹力秤,用来测量某段时间的降雨量。其原理如图甲所示,它主要由轻质弹簧,轻质杠杆OAB,压力传感器R(电阻值随所受压力的大小发生变化的变阻器)和显示压力大小的仪器A(实质是电流表)等关键元件构成,其中OA:OB=1:2,已知压力传感器的电阻R与它所受的压杆压力F的关系如图乙所示。电源电压为6V且保持不变,真真将一个质量为600g,棱长为10cm的实心正方体木块悬挂在弹簧下端,静止时木块下表面距离空烧杯底正上方4cm处,若烧杯底面积为300cm2,轻质弹簧自然状态时长度为10cm,且弹簧每受到1N的力时长度变化0.5cm,杠杆始终水平。当水槽内收集一些水时;
(1)弹簧恰好处于自然状态,求此时通过仪器A的电流;
(2)若仪器A示数为0.2A时,求物体排开水的体积V排;
(3)仪器A示数为0.2A时,求水槽中水的总质量。
32.如图甲所示,小王同学设计了一个汽车落水安全装置并进行了试验,在汽车的四个门板外侧分别安装一个气囊,气囊的触发由图乙所示电路中a、b间的电压来控制,压敏电阻R1水平安装在汽车底部A处,R1的阻值随其表面水的压力的变化如图丙所示。
某次试验时:汽车入水前把R2的滑片调到合适位置不动,闭合开关S,电压表的示数为4V,再把汽车吊入足够高的长方体水池中缓慢下沉,直到a、b间的电压等于或大于4V时,气囊就充气打开,使汽车漂浮在水中,试验装置相关参数如表所示。
电源电压 6V
R1接触水的面积 15cm2
长方体水池底面积 25m2
(1)求汽车入水前电路中R1的电流;
(2)当汽车漂浮时,测得水池的水位比汽车入水前上升了10cm(水未进入车内),求汽车受到的重力;
(3)求气囊充气打开时汽车A处浸入水中的深度。
参考答案
【计算1并联电路的电流规律】
1.(1)电流表A1使用0~3A量程,示数为0.8A,A2使用0~0.6A量程,示数为0.48A;
(2)通过灯泡L1、L2的电流分别为0.32A、0.48A。
【分析】(1)对于电流表的读数,应结合电联电路的电流特点确定量程,再根据指针位置读出示数。
(2)分析电路图可知,灯L1和L2组成并联电路,电流表A1测通过干路的电流,电流表A2测通过灯L2的电流,在并联电路中干路中的电流等于各支路电流之和。
【解答】解:
(1)由图甲知,电流表A1测的是干路电流,电流表A2测的是灯L2支路的电流,由于并联电路干路电流等于各支路电流之和,则电流表A1的示数应大于电流表A2的示数;
由图乙知,电流表A1指针偏转角度小于A2,
所以电流表A1选择的量程是0~3A,读数是0.8A,即干路电流:I=0.8A,
电流表A2的量程是0~0.6A,读数是0.48A,即通过灯L2的电流大小为:I2=0.48A,
(2)由于并联电路干路电流等于各支路电流之和,则通过灯L1的电流大小为:I1=I﹣I2=0.8A﹣0.48A=0.32A。
答:(1)电流表A1使用0~3A量程,示数为0.8A,A2使用0~0.6A量程,示数为0.48A;
(2)通过灯泡L1、L2的电流分别为0.32A、0.48A。
2.(1)A的示数为1A;(2)电流表A1的示数是0.3A
【分析】由图知,两电阻并联,A1测R1支路的电流,电流表A2测R2支路的电流,电流表A测干路电流,由图2得出电流表A的示数,根据并联电路中干路电流等于各支路电流之和即可解答。
【解答】解:(1)由图知,两电阻并联,A1测L1支路的电流,电流表A2测L2支路的电流,电流表A测干路电流,
由图2可得:电流表A的量程为0~3A,则示数为1A:即:干路电流I=1A;
(2)因并联电路中干路电流等于各支路电流之和,所以电流表A1的示数:I1=I﹣I2=1A﹣0.7A=0.3A。
答:(1)A的示数为1A;(2)电流表A1的示数是0.3A。
3.流过电灯L1的电流是0.9A,流过电灯L2的电流为0.3A。
【分析】(1)根据图示可知,灯L1与灯L2并联,电流表A1测干路电流,电流表A2测L2电流。
(2)电流表量程不明,但根据电流表连入电路情况知,A1电流表测量干路的电流I,电流表A2测量通过支路L2的电流I2.A1的示数应大于A2的示数。
(3)根据指针的偏转情况可以判断A用的是0~3A的量程,A2用的是0~0.6A的量程。通过观察指针所指位置即可读数,然后利用并联电路电流规律:I=I1+I2,可求出电灯L1的电流。
【解答】解:(1)由图可知:灯L1与灯L2并联,电流表A1测干路电流,电流表A2测L2电流。
根据并联电路电流规律可知:干路电流大于支路电流。而从两表指针偏转位置来看,A2偏转的比A1还大,说明这两表使用的量程不同。由此得出:A2的量程为0~0.6A量程,A1的量程为0~3A量程。
0~0.6A量程的分度值是0.02A,所以A2的示数是0.3A,即I2=0.3A。
0~3A量程的分度值是0.1A,所以A1的示数是1.2A;即I=1.2A,
(2)根据并联电路电流规律:I=I1+I2,所以通过灯L1的电流:I1=I﹣I2=1.2A﹣0.3A=0.9A。
答:流过电灯L1的电流是0.9A,流过电灯L2的电流为0.3A。
4.通过灯泡L1的电流I1为1.1A,通过灯泡L2的电流I2为0.7A。
【分析】分析电路图可知,灯L1和L2组成并联电路,电流表A1测通过干路的电流,电流表A2测通过灯L2的电流,在并联电路中干路中的电流等于各支路电流之和,据此解答。
【解答】解:由图可知L1、L2并联,
电流表A1测干路电流:I=1.8A,
电流表A2测L2的电流:即I2=0.7A,
因为在并联电路中干路中的电流等于各支路电流之和,
所以流过L1的电流I1=I﹣I2=1.8A﹣0.7A=1.1A。
答:通过灯泡L1的电流I1为1.1A,通过灯泡L2的电流I2为0.7A。
5.(1)电流表A2的示数为0.1A,A3的示数为0A;
(2)电流表A1的示数为0.4A;
(3)若将S1、S2和S3同时闭合会发生电源短路现象。
【分析】(1)当S1闭合、S2和S3都断开时,两灯串联,电流表A1、A2测电路中的电流,由串联电路的电流特点可知A2和A1的示数;
(2)当S2和S3闭合、S1断开时,两灯并联,电流表A测干路电流,A1、A2分别测L1和L2支路的电流,由并联电路的电流特点可得A1示数;
(3)不经过用电器而直接跟电源两极相连的电路叫做电源短路。
【解答】解:
(1)根据电路图可知,当S1闭合、S2和S3都断开时,L1、L2串联,电流表A1和A2都测量电路中的电流,
电流表A1的示数如图乙所示,该电流表选用小量程,分度值为0.02A,则A1的示数为0.1A,
因串联电路中电流处处相等,故电流表A1和A2的示数相等,都等于0.1A;电流表A处于断路状态,因此其示数为0A;
(2)当S2和S3闭合、S1断开时,两灯并联,电流表A测干路电流,A1、A2分别测L1和L2支路的电流,
因并联电路中干路电流等于各支路电流之和,
所以当S2和S3闭合、S1断开时,电流表A1的示数:IA1=IA﹣IA2=0.7A﹣0.3A=0.4A;
(3)当S1、S2和S3同时闭合时,电流从电源正极流出,直接从S1、S3回到电源负极,故发生电源短路,电源将被烧坏。
答:(1)电流表A2的示数为0.1A,A的示数为0A;
(2)电流表A1的示数为0.4A;
(3)若将S1、S2和S3同时闭合会发生电源短路现象。
【计算2 串联电路的电压规律】
6.(1)L1两端电压为1.2V,L2两端的电压为4.8V;
(2)通过L2的电流为0.3A,L2两端的电压为6V。
【分析】(1)由图甲所示电路图可知,两灯泡串联,电压表V1测电源电压,电压表V2测L1两端电压;
根据电压表所测电路电压与指针偏转情况确定两电压表量程,读出其示数,然后求出两灯泡两端电压;
(2)由图丙所示电路可知,两灯泡并联,电流表A1测L1支路电流,电流表A2测干路电流,由并联电路特点求出通过灯泡的电流、求出灯泡两端电压。
【解答】解:
(1)由图甲所示电路图可知,两灯泡串联,电压表V1测电源电压,电压表V2测L1两端电压;
串联电路总电压大于部分电路电压,由图乙所示电压表可知,两电压表指针位置相同,
则电压表V1的量程为0~15V,示数为6V,电压表V2的量程为0~3V,示数为1.2V;
则灯L1两端电压为1.2V,灯L2两端电压:
U2=U﹣U1=6V﹣1.2V=4.8V;
(2)由图丙所示电路可知,两灯泡并联,电流表A1测L1支路电流,电流表A2测干路电流,
通过L2的电流:
I2=I﹣I1=1.5A﹣1.2A=0.3A,
灯L2并联在电源两端,电源电压为6V,则L2两端电压为6V。
答:(1)L1两端电压为1.2V,L2两端的电压为4.8V;
(2)通过L2的电流为0.3A,L2两端的电压为6V。
7.(1)当开关S1、S2都闭合时通过电灯L1的电流。为0.36A;
(2)当开关S闭合时电灯L2两端的电压为3.6V。
【分析】(1)当开关S1、S2都闭合时,两灯泡并联接入电路,电流表测干路电流,当开关S1断开、S2闭合时,电路为灯泡L2的简单电路,电流表测通过电路的电流,根据并联电路电流规律计算当开关S1、S2都闭合时通过电灯L1的电流;
(2)当开关S闭合后,两灯泡串联接入电路,电压表V1测灯泡L1两端的电压,电压表V2测电源电压,根据串联电路电压规律计算当开关S闭合时电灯L2两端的电压。
【解答】解:(1)当开关S1、S2都闭合时,两灯泡并联接入电路,电流表测干路电流,电流表的示数为0.58A;
当开关S1断开、S2闭合时,电路为灯泡L2的简单电路,电流表测通过电路的电流,电流表的示数为0.22A,
根据并联电路不相互影响,通过L2的电流不变,
并联电路干路电流等于各支路电流之和,所以当开关S1、S2都闭合时通过电灯L1的电流:I1=I﹣I2=0.58A﹣0.22A=0.36A;
(2)当开关S闭合后,两灯泡串联接入电路,电压表V1测灯泡L1两端的电压,电压表V2测电源电压,
串联电路总电压等于各部分电压之和,电压表V1、V2的示数分别为2.2V和5.8V,
则当开关S闭合时电灯L2两端的电压:U2=U﹣U1=5.8V﹣2.2V=3.6V。
答:(1)当开关S1、S2都闭合时通过电灯L1的电流。为0.36A;
(2)当开关S闭合时电灯L2两端的电压为3.6V。
8.(1)电压表V的示数是6V;
(2)此电源需要4个干电池串联而成.。
【分析】串联电路两端电压等于各部分电压之和,一节干电池的电压为1.5V。
【解答】解:图中,两个灯泡串联,电压表V1测L1两端电压,电压表V2测量L2两端电压,电压表V测量电源电压;因为串联电路两端电压等于各部分电压之和,因此V的示数为2V+4V=6V;而一节干电池电压为1.5V,因此需要4节干电池串联连接。
答:(1)电压表V的示数是6V;
(2)此电源需要4个干电池串联而成.。
9.(1)电源电压是4.5V;
(2)流过灯L1和L2的电流都是0.24A;
(3)L1和L2两端的电压分别是3.3V和1.2V。
【分析】(1)一节新干电池的电压为1.5V,电源由三节新干电池串联组成,据此计算电源电压;
(2)由乙图可知电流表接入电路的量程和分度值,闭合开关,两灯泡串联接入电路,根据串联电路电流特点可知流过灯L1和L2的电流分别是多少;
(3)电压表与所测灯泡并联接入电路,电压表V1测电源电压,电压表V2测灯泡L1两端的电压,分析电压表接入电路的量程,明确电压表的分度值,根据串联电路电压规律计算灯L2两端的电压。
【解答】解:(1)电源由三节新干电池串联组成,所以电源电压为:U=3×1.5V=4.5V;
(2)闭合开关,两灯泡串联接入电路,串联电路各处电流相等,电流表测通过电路的电流,由乙图可知电流表接入电路的量程为0~0.6A,分度值为0.02A,示数为0.24A,所以流过灯L1和L2的电流都是0.24A;
(3)电压表V1测电源电压,电压表V2测灯泡L2两端的电压,则电压表V2接入电路的量程为0~3V,分度值为0.1V,示数为1.2V,
串联电路总电压等于各部分电压之和,所以灯L1两端的电压为:U1=U﹣U2=4.5V﹣1.2V=3.3V。
答:(1)电源电压是4.5V;
(2)流过灯L1和L2的电流都是0.24A;
(3)L1和L2两端的电压分别是3.3V和1.2V。
【计算3 欧姆定律公式的应用】
10.见试题解答内容
【分析】由电路图可知,R1与R2并联,电压表测电源的电压,电流表测干路电流。
(1)根据并联电路的电压特点和欧姆定律求出通过电阻R1的电流;
(2)根据并联电路的电流特点求出通过R2的电流,根据欧姆定律求出电阻R2的阻值。
【解答】解:由电路图可知,R1与R2并联,电压表测电源的电压,电流表测干路电流。
(1)因并联电路中各支路两端的电压相等,
所以,通过电阻R1的电流:
I1===0.2A。
(2)因并联电路中干路电流等于各支路电流之和,
所以,通过R2的电流:
I2=I﹣I1=0.5A﹣0.2A=0.3A,
由欧姆定律得,电阻R2的阻值:
R2===20Ω。
答:(1)通过电阻R1的电流为0.2A;
(2)电阻R2的阻值为20Ω。
11.(1)通过电阻R2的电流为0.5A;
(2)电阻R2的阻值为60Ω。
【分析】(1)由电路图可知,同时闭合开关S1、S2时,R1、R2并联,电流表测干路中的电流,根据欧姆定律求出通过电阻R1的电流,根据并联电路中干路电流等于各支路电流之和求出通过电阻R2的电流;
(2)根据I=求出电阻R2的阻值。
【解答】解:(1)由电路图可知,同时闭合开关S1、S2时,R1、R2并联,电流表测干路中的电流,
则通过电阻R1的电流:
I1===2A;
根据并联电路中干路电流等于各支路电流之和知通过电阻R2的电流为:
I2=I﹣I1=2.5A﹣2A=0.5A;
(2)根据I=得电阻R2的阻值:
R2===60Ω。
答:(1)通过电阻R2的电流为0.5A;
(2)电阻R2的阻值为60Ω。
12.①电阻R1的阻值是20Ω;②电阻R2的阻值是60Ω;③推导过程见解答过程。
【分析】由电路图知两电阻串联,电流表测量电路的电流,电压表测量R1两端电压;
①根据欧姆定律计算电阻R1的阻值;
②根据串联电路电压特点和欧姆定律计算电阻R2的阻值;
③根据串联电路电流、电压特点和欧姆定律推导串联电路总电阻。
【解答】解:
①由电路图知两电阻串联,且I=I1=I2=0.1A,U1=2V,则R1===20Ω;
②由串联电路电压特点得,U2=U﹣U1=8V﹣2V=6V,则R2===60Ω;
③设电阻R1两端的电压为U1,电阻R2两端的电压为U2,电阻R1、R2两端的总电压为U,电阻R1、R2的总电阻为R,由于电阻R1、R2串联,通过两电阻的电流相等,设电路中的电流为I,
则由I=得:U1=R1I1=R1I,U2=R2I2=R2I,U=RI,
由串联电路的电压规律可知U=U1+U2,
即RI=R1I1+R2I2=R1I+R2I
所以R=R1+R2。
答:①电阻R1的阻值是20Ω;②电阻R2的阻值是60Ω;③推导过程见解答过程。
13.(1)滑动变阻器最大阻值为20Ω;
(2)电源电压为6V,R1的阻值为10Ω;
(3)滑片P滑到ab中点时电压表的示数为3V。
【分析】由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(1)当滑动变阻器滑片P在a端时,滑动变阻器接入电路中的电阻最大,电路中的电流最小,根据图乙读出电路中的最小电流和电压表的示数,根据欧姆定律求出滑动变阻器的最大阻值;
(2)当滑动变阻器滑片P在a端时,根据串联电路的电压特点和欧姆定律表示出电源的电压;当滑动变阻器滑片P在b端时,接入电路中的电阻为零,此时电路中的电流最大,根据图乙读出电路中的最大电流,利用欧姆定律求出电源的电压,然后联立等式求出R1的阻值和电源的电压;
(3)当滑片P滑到ab中点时,根据电阻的串联和欧姆定律求出电路中的电流,利用欧姆定律求出电压表的示数。
【解答】解:由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(1)当滑动变阻器滑片P在a端时,滑动变阻器接入电路中的电阻最大,电路中的电流最小,
由图乙可知,电路中的最小电流I小=0.2A,电压表的示数U2=4V,
由I=可知,滑动变阻器的最大阻值:R2===20Ω;
(2)当滑动变阻器滑片P在a端时,
因串联电路中总电压等于各分电压之和,所以,电源的电压U=I小R1+U2=0.2A×R1+4V﹣﹣﹣﹣﹣①
当滑动变阻器滑片P在b端时,接入电路中的电阻为零,此时电路中的电流最大,
由图乙可知,电路中的最大电流I大=0.6A,
则电源的电压U=I大R1=0.6A×R1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
由①②可得:R1=10Ω,U=6V;
(3)当滑片P滑到ab中点时,接入电路中的电阻R2′=R2=×20Ω=10Ω,
因串联电路中总电阻等于各分电阻之和,所以,电路中的电流I====0.3A,
则电压表的示数U2′=IR2′=0.3A×10Ω=3V。
答:(1)滑动变阻器最大阻值为20Ω;
(2)电源电压为6V,R1的阻值为10Ω;
(3)滑片P滑到ab中点时电压表的示数为3V。
14.①此时滑动变阻器R连入电路的阻值为17.5Ω。
②移动变阻器滑片P可以使电流表的最大值和最小电流分别为2A、0.7A。
【分析】①由电路图可知,只有R连入电路,电流表测电路中的电流,利用欧姆定律求出滑动变阻器R连入电路的阻值。
②根据图可知电流表的量程和滑动变阻器的规格即可判断电路中的最大电流;
当滑动变阻器接入电路的电阻最大时,电路中的电流最小;根据欧姆定律求出电路最小电流。
【解答】解:
①由电路图可知,只有R连入电路,电流表测电路中的电流,
由图2可知:电流表的量程是0~3A,则示数为0.8A,
由欧姆定律可得,滑动变阻器R连入电路的阻值:R′===17.5Ω;
②由于电流表的量程是0~3A,滑动变阻器标有“20欧 2安”字样
则电路中的最大电流为2A;
当滑动变阻器接入电路的电阻最大时,由欧姆定律可知通过电路的电流最小,
最小电流为:I小===0.7A。
答:①此时滑动变阻器R连入电路的阻值为17.5Ω。
②移动变阻器滑片P可以使电流表的最大值和最小电流分别为2A、0.7A。
15.(1)此时电路中Rt的电阻是400Ω;
(2)当电流表示数为0.01A时,环境温度是20℃;
(3)当环境温度为30℃,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,电源电压是6V;
(4)若温度为40℃,则电阻箱允许接入电路的阻值调节范围是100Ω~200Ω。
【分析】根据电路图可知,R1、Rt串联,电流表测量电路电流。
(1)(2)根据欧姆定律求出电阻箱接入电路的阻值;根据串联电路电压规律求出Rt两端电压,再根据欧姆定律求出Rt的阻值,并从图乙中读出此时的环境温度;
(3)由图乙可知,环境温度为40℃时热敏电阻的阻值,根据电流表的量程得出电路中的最大电流,根据欧姆定律求出电路的最小总电阻,利用电阻的串联求出电阻箱接入电路中的最小阻值,然后得出电阻箱允许的阻值调节范围。
【解答】解:由电路图可知,R1与Rt串联,电流表测电路中的电流。
(1)根据欧姆定律可知此时电路中Rt的电阻:Rt===400Ω;
(2)当电流表示数为0.01A时,Rt的电阻为400Ω,从图乙可知环境温度是20℃;
(3)设电源电压为U,则U=+,
当电流表示数为0.01A时,U=0.01A×R+4V…①
当环境温度为30℃,从图乙可知Rt的阻值为300Ω,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,
则:U=0.015A×0.5R+0.015A×300Ω…②
由①②解出解出U=6V;
(4)由图乙可知,环境温度为40℃时,热敏电阻的阻值Rt=200Ω,
由电流表的量程为0~0.6A和电阻箱允许通过的最大电流为0.02A可知,电路中的最大电流I大=0.02A,
则电路的最小总电阻:R总′===300Ω,
所以,电阻箱接入电路中的最小阻值:R1′=R总′﹣Rt=300Ω﹣200Ω=100Ω,
电压表的量程是0﹣3V,故电阻箱两端的电压最大为3V,此时Rt两端的电压为=6V﹣3V=3V,
根据欧姆定律及串联分压特点可知,电路中电流I小===0.015A,
此时变阻器接入电路的阻值最大,为R1″===200Ω,
则电阻箱允许接入电路的阻值调节范围是100Ω~200Ω。
答:(1)此时电路中Rt的电阻是400Ω;
(2)当电流表示数为0.01A时,环境温度是20℃;
(3)当环境温度为30℃,将电阻箱的阻值调为0.5R时,发现电流表示数为0.015A,电源电压是6V;
(4)若温度为40℃,则电阻箱允许接入电路的阻值调节范围是100Ω~200Ω。
16.(1)电源电压U为3V,电源内阻r为1Ω;
(2)当滑动变阻器的滑片处于中点时,电源内阻r的电压为0.15V,通过电源内阻r的电流为0.15A。
【分析】(1)如图乙所示,电阻R1、滑动变阻器R2、电源内部电阻r三者串联。
当滑动变阻器位于a点时,根据欧姆定律电源电压U=Ia(R1+R2+r)①,
当滑动变阻器位于b点时,根据欧姆定律电源电压U=Ib(R1+r)②,
①②式联立求出电源电压U和电阻r;
(2)根据欧姆定律I=计算滑动变阻器的滑片处于中点时电路中的电流,根据欧姆定律U=IR计算电源内阻r的电压。
【解答】解:(1)如图乙所示,电阻R1、滑动变阻器R2、电源内部电阻r三者串联。
当滑动变阻器位于a点时,滑动变阻器完全接入电路,此时电路电流最小为0.1A,R1=9Ω,滑动变阻器R2的最大值为20Ω,
根据欧姆定律可得,电源电压U=Ia(R1+R2+r)=0.1A×(9Ω+20Ω+r)……①,
当滑动变阻器位于b点时,滑动变阻器不接入电路,此时电路电流最大为0.3A,
根据欧姆定律可得,电源电压U=Ib(R1+r)=0.3A×(9Ω+r)……②,
①②式联立解得,电源电压U=3V,电源内阻r=1Ω;
(2)当滑动变阻器的滑片处于中点时,接入电路的阻值为10Ω,根据欧姆定律可得,
此时电路中的电流I====0.15A,
串联电路电流相等,故通过电源内阻r的电流为0.15A,
电源内阻r的电压Ur=Ir=0.15A×1Ω=0.15V。
答:(1)电源电压U为3V,电源内阻r为1Ω;
(2)当滑动变阻器的滑片处于中点时,电源内阻r的电压为0.15V,通过电源内阻r的电流为0.15A。
17.见试题解答内容
【分析】由电路图可知,R1与R2串联,电压表测R1两端的电压,电流表测电路中的电流。
(1)根据欧姆定律求出电阻R1的阻值;
(2)当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,根据电阻的串联和欧姆定律求出电路中的最小电流;
(3)根据滑动变阻器的铭牌可知电路中的最大电流,根据欧姆定律求出电路中的总电阻,利用电阻的串联求出R2的最小阻值,然后得出滑动变阻器R2连入电路的阻值范围。
【解答】解:由电路图可知,R1与R2串联,电压表测R1两端的电压,电流表测电路中的电流。
(1)由I=可得,电阻R1的阻值:
R1===5Ω;
(2)当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,
因串联电路中总电阻等于各分电阻之和,
所以,电路中的最小电流:
I小===0.5A;
(3)由题意可知,电流表量程为0~3A,而滑动变阻器允许通过的最大电流为2A,
所以,为了保证电路的安全,电路中的最大电流I大=2A,此时变阻器接入电路中的电阻最小,
此时电路中的总电阻:
R===8Ω,
则滑动变阻器接入电路中的最小阻值:
R2小=R﹣R1=8Ω﹣5Ω=3Ω,
当变阻器接入电路中的电阻最大为27Ω时,电路中电流最小,电压表示数最小,各电路元件是安全的,
所以变阻器R2的阻值范围为3Ω~27Ω。
答:(1)电阻R1的阻值为5Ω;
(2)电路中的最小电流为0.5A;
(3)滑动变阻器R2连入电路的阻值范围为3Ω~27Ω。
18.(1)R1阻值为5Ω;
(2)当S2闭合,S1、S3断开时,电压表示数为2V;
(3)当S1、S3闭合,S2断开时,电流表示数为0.6A。
【分析】(1)当S1闭合,S2、S3断开时,只有R1连入电路中,根据欧姆定律计算R1的阻值;
(2)当S2闭合,S1、S3断开时,R1与R2串联,电压表V测测R2两端的电压,根据串联电路的电阻规律和欧姆定律计算通过电路的电流,根据U=IR计算电压表的示数;
(3)当开关S1、S3闭合,S2断开时,R1与R2并联,电流表测通过R1的电流,根据并联电路电压特点结合欧姆定律计算通过R1的电流,进一步确定电流表示数。
【解答】解:(1)由电路图知,当S1闭合,S2、S3断开时,只有R1连入电路中,电流表测通过R1的电流,
由欧姆定律可得R1阻值为:R1===5Ω;
(2)由电路图知,当S2闭合,S1、S3断开时,R1与R2串联,电压表V测R2两端的电压,电流表测量电路的电流,
串联电路总电阻等于各部分电阻之和,则电路总电阻:R=R1+R2=5Ω+10Ω=15Ω,
根据欧姆定律可得通过电路的电流为:I′===0.2A,
则电阻R1两端的电压:U1=I′R2=0.2A×10Ω=2V,即电压表示数为2V;
(3)当开关S1、S3闭合,S2断开时,R1与R2并联,电流表测通过R1的电流,
并联电路各支路两端电压相等,根据欧姆定律可得通过R1的电流:I1===0.6A,即电流表示数为0.6A。
答:(1)R1阻值为5Ω;
(2)当S2闭合,S1、S3断开时,电压表示数为2V;
(3)当S1、S3闭合,S2断开时,电流表示数为0.6A。
19.(1)电源电压为12V;
(2)电流表A的示数为0.9A。
【分析】由电路图可知,R1与R2并联,电流表A测干路电流,电流表A1测R1支路的电流。
(1)根据并联电路的电压特点结合欧姆定律求出电源电压;
(2)根据并联电路的电流规律结合欧姆定律计算电流表A的示数。
【解答】解:由电路图可知,R1与R2并联,电流表A测干路电流,电流表A1测R1支路的电流。
(1)并联电路各支路两端电压相等,都等于电源电压,
由欧姆定律可得电源电压:U=I1R1=0.6A×20Ω=12V;
(2)并联电路干路电流等于各支路电流之和,根据欧姆定律可得电流表A的示数:I=I1+I2=I1=0.6A+=0.9A。
答:(1)电源电压为12V;
(2)电流表A的示数为0.9A。
20.(1)深度表在水面上时,电路中的电流约为0.1A;
(2)电压表示数为2V时,潜水员下潜的深度为10m;
(3)在保证电路安全的情况下,该深度表能浸入水中的最大深度为40m。
【分析】(1)由图乙可知,该电路为R0和RP的串联电路,电压表测R0两端的电压,深度表在海面上深度为0m时,由图丙可知,此时RP阻值,由串联电路的电阻特点和欧姆定律可知电路中的电流;
(2)已知电压表示数为2V时,由欧姆定律可得通过R0的电流,由串联电路的电流特点和电压特点可知RP两端的电压,再求此时RP的阻值,对照图丙可知此时潜水员下潜的深度为;
(3)当电路中电流最大时,R0两端的电压最大为电压表量程的最大值,可得电路中最大电流且小于0.24A,由欧姆定律算出此时电路总电阻,由串联电路的电阻特点可知压敏电阻RP的阻值,对照图丙可知,此时下潜的深度即为该深度表能测量的最大深度。
【解答】解:(1)由图乙可知,该电路为R0和RP的串联电路,电压表测R0两端的电压;
深度表在海面上时,即h=0m时,由图丙可知,此时RP=40Ω,
由串联电路的电阻特点和欧姆定律可知电路中的电流为:I===≈0.1A;
(2)已知电压表示数为2V时,即R0两端的电压为U0=2V,
通过R0的电流为I0===A,即电路中的电流为I′=I0=A,
由串联电路的电压特点可知RP两端的电压为:UP=U﹣U0=6V﹣2V=4V,
则此时RP的阻值为:RP′===30Ω,
由图丙可知,此时潜水员下潜的深度为h′=10m;
(3)当电路中电流最大时,由U=IR可知R0两端的电压最大,
由电压表量程可知R0两端的电压最大为:U0大=3V,
由此可知电路中电流最大为:I大===0.2A<0.24A,
为保护电路,电路中允许通过的最大电流为0.2A,
此时电路总电阻为:R总===30Ω,
由串联电路的电阻特点可知压敏电阻RP的阻值为:RP=R总﹣R0=30Ω﹣15Ω=15Ω,
由图丙可知,此时下潜的深度为40m,即该深度表能测量的最大深度为40m。
答:(1)深度表在水面上时,电路中的电流约为0.1A;
(2)电压表示数为2V时,潜水员下潜的深度为10m;
(3)在保证电路安全的情况下,该深度表能浸入水中的最大深度为40m。
【计算4 欧姆定律与浮力杠杆的综合计算】
21.(1)定值电阻R0的阻值为10Ω;
(2)当平板空载时,电压表的示数为4V;
(3)如果只水平调节杠杆上触点B的位置,则触点B应向右移动,移动3cm。
【分析】(1)压力传感器和定值电阻串联接入电路,电压表测定值电阻两端的电压,由表格可知当平板空载时压力传感器的阻值,根据串联电路电压规律和电流特点,结合欧姆定律计算定值电阻R0的阻值;
(2)平板上物体对平板的压力等于自身的重力,根据杠杆平衡条件可得杠杆B点受到的压力,由力的作用是相互的可知压力传感器受到的压力,由表格可知此时压敏电阻的阻值,根据串联电路电阻规律结合欧姆定律计算此时通过电路的电流,进一步计算此时电压表的示数;
(3)电池组用久后电压变小,电路中电流变小,要增大电路中电流,需减小压力传感器的电阻,就要增大压力传感器受到的压力,其它条件不变,由杠杆平衡条件可知,需向右调节B触点,设调节距离为L,此时压力传感器阻值为R′′,利用欧姆定律求其大小;从图象可知传感器受到的压力,由于力的作用是相互的,可求杠杆A点受到的压力,利用杠杆平衡条件求L的大小。
【解答】解:(1)压力传感器和定值电阻串联接入电路,电压表测定值电阻两端的电压,
由表格可知当平板空载时,压力传感器的阻值为70Ω,
因串联电路总电压等于各部分电压之和,串联电路各处电流相等,
则由欧姆定律可得:=,即=,
解得:R0=10Ω;
(2)平板上物体对平板的压力:FB=G=120N,
由题知,AB:OB=5:1,则OA:OB=6:1,
由杠杆平衡条件FA×OA=FB×OB得杠杆A点受到的压力:FA=FB=×120N=20N,
由于力的作用是相互的,压力传感器受到的压力为20N,
由表格可知压敏电阻的阻值:R′=20Ω,串联电路总电阻等于各分电阻之和,
由欧姆定律得:I====0.4A,
此时电压表的示数;U0′=IR0=0.4A×10Ω=4V;
(3)电源用久后电压变小,电路中电流变小,若要求此时平板上重为120N的物体对应的电压表示数和电源电压为12V的情况下相同,则需减小压力传感器的电阻,就要增大压力传感器受到的压力,其它条件不变,由杠杆平衡条件可知,需向右移动B触点,设调节距离为L,此时压力传感器阻值为R′′,
因为此时电压表示数和R0的阻值不变,所以由欧姆定律可知电路中电流不变,仍然为0.4A,
则此时的电源电压:U1=IR总′=I(R′′+R0),
即9V=0.4A×(R′′+10Ω),
解得R′′=12.5Ω,
由表格可知可知传感器受到的压力为23N,
由于力的作用是相互的,杠杆A点受到的压力为:FA′=23N,
由杠杆平衡条件可得:
FA′×OA=FB×(OB+L),
23N×1.2m=120N×(×1.2m+L),解得:L=0.03m=3cm。
答:(1)定值电阻R0的阻值为10Ω;
(2)当平板空载时,电压表的示数为4V;
(3)如果只水平调节杠杆上触点B的位置,则触点B应向右移动,移动3cm。
22.(1)电源电压为6V,物体M所受的重力为22.5N;
(2)当物体M完全浸没时所受的浮力为7.5N;
(3)物体M的密度是3×103kg/m3。
【分析】(1)由图甲可知:电阻R0与滑动变阻器R串联,电压表测量滑动变阻器R两端的电压,电流表测量电路中电流;
由图丙读出电压表示数,根据欧姆定律和串联电路的特点求出电源电压;
根据欧姆定律求出变阻器接入电路的阻值,根据图乙得到拉力;
结合图丙分析得出具体的物理过程,深度为0~h1时,物体M不受浮力,此时拉力等于重力;
(2)深度大于h2时,物体M浸没在水中,拉力最小;由图丙读出水面深度为h2时电压表的示数,根据欧姆定律和串联电路的特点求出变阻器接入电路的阻值,根据图乙得到拉力;根据称重法测浮力公式可得物体M浸没在水中时所受的浮力;
(3)利用F浮=ρ水gV排可得物体M的体积,最后利用密度公式可求出物体M的密度。
【解答】解:(1)由电路图可知,R0与R串联,电压表测R两端的电压,电流表测电路中的电流;
当水面深度到达h1时,由图丙可知,电压表的示数U1=2V,
根据欧姆定律和串联电路的特点可得电源电压:
U=U0+U1=I1R0+U1=0.4A×10Ω+2V=6V;
根据I=可得变阻器接入电路的阻值为:
R1===5Ω,
由图乙可知,此时拉力F1=22.5N,
由于是往容器中缓慢注水,结合图丙可知:
当容器内水的深度在0~h1时,物体M没有浸在水中,不受浮力,此时弹簧的拉力与重力平衡,拉力最大;当容器内水的深度在h1~h2时,物体M浸在水中受浮力的作用,水的深度增加,浮力增大,拉力减小;当容器内水的深度大于h2时,物体M浸没在水中,浮力最大且不变,此时拉力最小。
结合上述分析可知:物体M所受的重力G=F1=22.5N,
(2)当水面深度到达h2时,由图丙可知,电压表的示数U2=4V,
因串联电路中总电压等于各分电压之和,
R0两端的电压:U0′=U﹣U2=6V﹣4V=2V,
电路中的电流:I2===0.2A,
根据I=可得变阻器接入电路的阻值为:
R2===20Ω,
由图乙可知,物体M浸没在水中时拉力为F2=15N;
根据称重法测浮力可知,物体M浸没在水中时受到的浮力:
F浮=G﹣F2=22.5N﹣15N=7.5N;
(3)根据F浮=ρ水gV排可得物体M的体积:
V=V排===7.5×10﹣4m3;
物体M的密度:ρ====3×103kg/m3。
答:(1)电源电压为6V,物体M所受的重力为22.5N;
(2)当物体M完全浸没时所受的浮力为7.5N;
(3)物体M的密度是3×103kg/m3。
23.(1)汽车入水前电路中的电流为0.075A;
(2)汽车受到的重力为1.8×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
【分析】(1)汽车入水前,R1表面水的压力为0,由图丙可知此时其阻值为20Ω,由乙图知R1和R2组成串联电路,电压表测的是R2两端的电压,示数为3V,已知总电压,根据串联电路的电压规律求出R1两端的电压,利用欧姆定律求出汽车入水前电路中的电流I;
(2)根据水池的水位比汽车入水前上升的高度,求出汽车排开水的体积,利用阿基米德原理求出汽车受到的浮力,根据汽车漂浮时,受到的重力和浮力平衡,大小相等,可求汽车受到的重力;
(3)先利用(1)中信息求出电阻R2的阻值,根据题中信息:汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于3V,即R1两端的电压为3V时,气囊充气打开,求出此时R2两端的电压,利用欧姆定律求出电路中的电流I′,利用欧姆定律求出电阻R1的阻值,由图丙可知,此时R1表面水的压力,即汽车底部A处受到水的压力,利用p=求出汽车A处受到水的压强,利用p=ρgh求出汽车A处浸入水中的深度。
【解答】解:(1)汽车入水前R1表面受到水的压力为0,由图丙可知此时R1的阻值为20Ω,由乙图可知R1和R2串联,电压表测R2两端的电压,示数为3V,根据串联电路的电压规律可知R1两端的电压为:
U1=U﹣U2=4.5V﹣3V=1.5V,
电路中的电流为:;
(2)当汽车漂浮时,水池的水位比汽车入水前上升了9cm,水池内水上升的体积即为汽车排开水的体积,则汽车排开水的体积为:
V排=S水池Δh=20m2×9×10﹣2m=1.8m3,
根据阿基米德原理可知:汽车受到的浮力为:
F浮=ρ水gV排=1.0×103kg/m3×10N/kg×1.8m3=1.8×104N,
当汽车漂浮时,汽车受重力和浮力,这两个力是一对平衡力,大小相等,则汽车受到的重力为:
G=F浮=1.8×104N;
(3)汽车入水前,电压表的示数为3V时,
则电阻R2的阻值为:
,
汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于3V,即此时R1两端的电压为3V,气囊充气打开,此时R2两端的电压为:
U2′=U﹣U1′=4.5V﹣3V=1.5V,
电路中的电流为:
I'===0.0375A,
电阻R1的阻值为:,
由图丙可知,此时R1表面水的压力为15N,即汽车底部A处受到水的压力为15N,汽车A处受到水的压强为:
汽车A浸入水中的深度为:
。
答:(1)汽车入水前电路中的电流为0.075A;
(2)汽车受到的重力为1.8×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
24.(1)当水深H=5cm时,水对容器底的压强为500Pa;
(2)木块A的重力5N;
(3)图中对应H0的值为28cm。
【分析】(1)已知水的密度和水的深度,根据p=ρgH算出当水深H=5cm时,水对容器底的压强;
(2)分析图2可知,当水深超过5cm时,电压表开始有示数,表明此时木块A刚好开始离开容器底,处于漂浮状态,根据漂浮条件G=F浮=ρ水gSH可求出木块A的重力;
(3)根据图丙可知,当R1两端的电压分别为1.5V、3.0V时R1消耗的电功率,根据I=分别求出电路中的电流,再根据串联电路的电压规律和欧姆定律分别列出电源电压的表达式,联立方程组求出电源电压、R2的阻值,当水深为10cm时根据欧姆定律求出此时R1的阻值,求出滑片上移的距离,进而求出滑动变阻器每1cm的电阻为1Ω,由图2可知,当水位到达H0后,电压表示数不再增加,表明此时滑片处于最上端即最大阻值处,根据图丙确定此时变阻器消耗的电功率,根据P2=I2R大求出滑动变阻器的最大阻值,求出对应的电阻丝的长度,由图丙可知,当水位在10~13cm时,电压表示数不变,表明接入电阻不变,求出短路部分的长度,即可解答。
【解答】解:(1)根据液体压强公式p=ρgh可得当水深H=5cm时,水对容器底的压强为:p=ρ水gH=1.0×103kg/m3×10N/kg×5×10﹣2m=500Pa;
(2)根据图丙可知,当水深超过5cm时,电压表开始有示数,表明此时木块A刚好开始离开容器底,处于漂浮状态,
根据物体沉浮条件可知木块A的重力为:G=F浮=ρ水gV排=ρ水gHS=1.0×103kg/m3×10N/kg×5×10﹣2m×0.01m2=5N;
(3)由图丙可知,当R1两端电压U1=1.5V时,功率为P1=1.125W,由P=UI可知此时电路中的电流为:I1===0.75A,
则电源电压为:U=U1+I1R2=1.5V+0.75A×R2……①,
当R1两端电压U2=3.0V时,功率为P2=1.8W,由P=UI可知此时的电流为:I2===0.6A,
则电源电压为:U=U2+I2R2=3.0V+0.6A×R2……②,
联立①②可得:U=9V,R2=10Ω,
当水深为10cm时,R1接入的电阻为:R1===5Ω,
此时滑片向上移动的距离为:d=10cm﹣5cm=5cm,
则滑动变阻器每1cm的电阻为1Ω;
当水位到达H0后,电压表示数不再增加,表明此时滑片处于最上端即最大阻值处,此时的R1的功率也为1.8W,则:
P2=I2R大=R大=R大=1.8W,
解方程可得:R大=5Ω或20Ω,
因为当水深为10cm时,R1接入的电阻为5Ω,则滑动变阻器最大阻值应为20Ω,
对应的电阻丝的长度为:L=1cm/Ω×20Ω=20cm,
由图丙可知,当水位在10~13cm时,电压表示数不变,表明接入电阻不变,
即短路部分的长度为:l=13cm﹣10cm=3cm,
所以图丙中对应H0的值为:H0=H+L+l=5cm+20cm+3cm=28cm。
答:(1)当水深H=5cm时,水对容器底的压强为500Pa;
(2)木块A的重力5N;
(3)图甲和乙中对应H0的值为28cm。
25.(1)当物体AB底面朝下放置在水平桌面上,对桌面产生的压强大小为5×103Pa;
(2)当物体AB上表面与水面相平时,物体AB受到的浮力大小30N;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,滑动变阻器R连入电路的阻值大小10Ω;
(4)当水面从物体AB上表面逐渐下降至下表面刚好离开水面的过程中,弹簧伸长了15cm。
【分析】(1)根据压力F=G和p=计算压强
(2)物体浸没时,V排=V物,根据阿基米德原理F浮=ρ液gV排可求浮力大小;
(3)根据串联电压特点计算定值电阻的电压,根据串联电压之比等于电阻之比确定滑动变阻器的电阻;
(4)利用图像可求力与伸长量的比值,再由弹簧弹力的变化可求弹簧的伸长量。
【解答】解:(1)当物体AB底面朝下放置在水平桌面上,F=G=50N,
压强p===5×103Pa;
(2)当物体AB上表面与水面相平时,物体AB刚好浸没水中V排=V物=Sh=0.01m2×0.3m=3×10﹣3m3;
物体AB所受浮力F浮=G排=ρ水gV排=1.0×103kg/m3×10N/kg×3×10﹣3m3=30N;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,R0的电压U0=U﹣UP=3V﹣1.5V=1.5V;
根据串联电路的电压之比等于电阻之比,两者电压相等,则电阻相等,因而R=R0=10Ω。
(4)水面与物体AB上表面相平时,弹簧对物体AB的拉力F弹=G物﹣F浮=50N﹣30N=20N;
水面下降至与物体AB下表面相平时,弹簧对物体AB的拉力F弹′=G物=50N;
水面从物体AB上表面逐渐下降至与下表面相平过程中,弹簧拉力的变化量ΔF弹=F弹'﹣F弹=50N﹣20N=30N;
由乙图可知:==2N/cm;
物体AB刚好离开水面时,弹簧伸长的长度ΔL′==15cm。
答:(1)当物体AB底面朝下放置在水平桌面上,对桌面产生的压强大小为5×103Pa;
(2)当物体AB上表面与水面相平时,物体AB受到的浮力大小30N;
(3)当水面从物体AB上表面逐渐下降至电压表示数为1.5V时,滑动变阻器R连入电路的阻值大小10Ω;
(4)当水面从物体AB上表面逐渐下降至下表面刚好离开水面的过程中,弹簧伸长了15cm。
26.(1)此时滑动变阻器R2接入电路中的阻值为20Ω;
(2)R2的滑片在位置M时,该液体密度计的“0”刻度线与电压表表盘1伏的刻度线相对应;
(3)该液体密度计的最大测量值为2.1g/cm3。
【分析】(1)由图可知,R0、R1和滑动变阻器R2串联,根据串联电路特点、欧姆定律计算出电路电流;
根据欧姆定律计算电路总电阻;
已知桶重和水重,要加班计算压敏电阻此时所受到的压力,由表格得出此时压敏电阻的阻值,根据串联电路电阻规律即可求出滑动变阻器接入电路中的阻值;
(2)不装液体时,密度计示数为0,由表格得出此时R1的阻值,根据串联电路的特点和欧姆定律计算出此时电压表的示数;
(3)根据表格数据可知压力越大时R1的阻值越小,所以据此可知当R2滑片在左端时R1的阻值最小,受到的压力最大;根据欧姆定律求出当电压表指针满偏时电路中的电流和此时电路中的总电阻以及R1的阻值最小值;根据图表可得R1与F之间的关系式,据此求出此时压敏电阻受到的最大压力,最后根据重力公式和密度公式计算出能够测量的最大密度。
【解答】解:(1)由图可知,R0、R1和滑动变阻器R2串联,电压表测量R0两端电压,已知在桶内注满水,闭合S,电压表的示数为1.5V,
串联电路各处电流相等,根据欧姆定律可得电路电流为:I=I0===0.15A,
根据欧姆定律可得此时总电阻为:R===80Ω;
此时压敏电阻受到的压力为:F=G水+G桶=1N+1N=2N,
由表格数据可知:F=2N时,R1=50Ω,
则根据串联电路的总电阻等于各分电阻之和可得,R2的电阻为:R2=R﹣R1﹣R0=80Ω﹣50Ω﹣10Ω=20Ω;
(2)该液体密度计的“0”刻线,即桶内不装液体时电压表的示数,由于当桶内不装液体时,压敏电阻受到的压力为空桶重力:F0=G桶=1N,
由表格数据可得:F0=1N时,R1′=90Ω,
根据串联电路的总电阻等于各分电阻之和可得:R′=R1′+R0+R2=90Ω+10Ω+20Ω=120Ω;
根据欧姆定律可得此时电压表示数为:U0′=×R0=×10Ω=1V,
即该液体密度计的“0”刻度线与电压表表盘1伏的刻度线相对应;
(3)当R滑全部接入时,滑动变阻器最大值为:R2大=24Ω,根据电压表的量程可知:U0大=3V,
根据欧姆定律可得此时电路中电流为:I1===0.3A,
根据欧姆定律可得此时总电阻为:R小===40Ω,
根据串联电路的总电阻等于各分电阻之和可得此时R1的电阻为:R1小=R小﹣R0﹣R2大=40Ω﹣10Ω﹣24Ω=6Ω,
根据图表可得R1与FB之间的关系式为:R1=130Ω﹣40Ω/N×F,
则此时压敏电阻受到的压力为:F大===3.1N,
则此时桶中液体的重力为:G液大=FA大﹣G桶=3.1N﹣1N=2.1N,
液体的质量为:m液大===0.21kg=210g,
则液体的密度为:ρ液大===2.1g/cm3。
答:(1)此时滑动变阻器R2接入电路中的阻值为20Ω;
(2)R2的滑片在位置M时,该液体密度计的“0”刻度线与电压表表盘1伏的刻度线相对应;
(3)该液体密度计的最大测量值为2.1g/cm3。
27.(1)当该电子秤恰好报警时,托盘所放物体的质量为30kg;
(2)托盘的支撑点B应向右移,移动的距离为8cm。
【分析】(1)闭合开关,两电阻串联接入电路,电压表测定值电阻两端的电压,
当电压表的示数等于或大于3V时,电子秤会自动发出报警声,根据欧姆定律计算此时通过电路的电流,根据串联电路电压规律计算此时力敏电阻两端的电压,根据欧姆定律计算此时力敏电阻接入电路的阻值,由表格可知力敏电阻受到的压力,
根据杠杆平衡条件可得F×OA=G×OB,据此计算托盘则物体是重力,根据m=计算托盘所放物体的质量;
(2)根据G=mg计算托盘上所放物体的重力,根据杠杆平衡条件可得F×OA=G′×OB′,进一步计算OB′,据此确定B点移动的方向,进一步计算托盘的支撑点B移动的距离。
【解答】解:(1)闭合开关,两电阻串联接入电路,电压表测定值电阻两端的电压,
当电压表的示数等于或大于3V时,电子秤会自动发出报警声,根据欧姆定律可得此时通过电路的电流I===0.5A,
串联电路总电压等于各部分电压之和,此时力敏电阻两端的电压U1=U﹣U2=15V﹣3V=12V,
此时力敏电阻接入电路的阻值R2===24Ω,
由表格可知力敏电阻受到的压力为150N,
根据杠杆平衡条件可得F×OA=G×OB,则托盘则物体是重力G==2F=2×150N=300N,
托盘所放物体的质量m===30kg;
(2)托盘上所放物体的重力G′=m′g=50kg×10N/kg=500N,
根据杠杆平衡条件可得F×OA=G′×OB′,则OB′===12cm,
则托盘的支撑点B应向右移×40cm﹣12cm=8cm。
答:(1)当该电子秤恰好报警时,托盘所放物体的质量为30kg;
(2)托盘的支撑点B应向右移,移动的距离为8cm。
28.(1)物体A的重力为80N;
(2)停止加水后物体A所受的浮力为20N;
(3)停止加水后物体A底部所受液体压强为500Pa;
(4)停止加水后容器底部所受液体压强为2500Pa。
【分析】(1)R1为竖直固定的光滑均匀金属棒,总电阻为20Ω,总长度为40cm,当弹簧下端不挂物体时,滑片P位于R1的最上端,当弹簧下端挂边长为20cm的立方体A时,滑片P位于R1的最下端,据此分析弹簧的形变量为40cm,由乙可知弹簧受到的拉力,物体A的重力等于弹簧受到的拉力;
(2)闭合开关,两电阻串联接入电路,电压表测滑片以上部分电阻两端的电压,根据串联电路电阻规律结合欧姆定律计算通过电路的电流,根据串联电路电流特点结合欧姆定律计算滑片以下部分的电阻,进一步计算滑片移动的距离和弹簧的形变量,由乙可知弹簧受到的拉力,
物体受到的浮力等于物体的重力与弹簧受到的拉力之差;
(3)根据阿基米德原理计算物体浸入水中的体积,根据体积公式计算物体浸入水中的深度,根据压强公式计算停止加水后物体A底部所受液体压强;
(4)滑片P位于R1的最下端时物体A的下端距容器底的距离h=10cm=0.1m,根据压强公式计算停止加水后容器底部所受液体压强。
【解答】解:(1)R1为竖直固定的光滑均匀金属棒,总电阻为20Ω,总长度为40cm,当弹簧下端不挂物体时,滑片P位于R1的最上端,当弹簧下端挂边长为20cm的立方体A时,滑片P位于R1的最下端,即弹簧的形变量为40cm,由乙可知弹簧受到的拉力为80N,则物体A的重力G=80N;
(2)闭合开关,两电阻串联接入电路,电压表测滑片以上部分电阻两端的电压,
串联电路总电阻等于各部分电阻之和,根据欧姆定律可得通过电路的电流:I===0.5A,
串联电路各处电流相等,滑片以下部分的电阻:RP===15Ω,
则滑片移动的距离为hP=×40cm=10cm,
弹簧的形变量为40cm﹣10cm=30cm,由乙可知弹簧受到的拉力为60N,
则物体受到的浮力为F浮=G﹣F=80N﹣60N=20N;
(3)物体浸入水中的体积:V排===2×10﹣3m3,
物体浸入水中的深度:h′===0.05m,
停止加水后物体A底部所受液体压强:p=ρ水gh′=1.0×103kg/m3×10N/kg×0.05m=500Pa;
(4)滑片P位于R1的最下端时物体A的下端距容器底的距离h=10cm=0.1m,
停止加水后容器底部所受液体压强:p′=ρ水g(h+hP+h′)=1.0×103kg/m3×10N/kg×(0.1m+0.1m+0.05m)=2500Pa。
答:(1)物体A的重力为80N;
(2)停止加水后物体A所受的浮力为20N;
(3)停止加水后物体A底部所受液体压强为500Pa;
(4)停止加水后容器底部所受液体压强为2500Pa。
29.(1)放入物体M前,电流表的示数为0.2A;
(2)M漂浮在水中时所受到的浮力为12N;
(3)当电流表的示数为0.3A时,物体M相对于漂浮在水中时移动的距离为1cm。
【分析】(1)通过图像得出放入物体前的电阻值,应用欧姆定律计算电流值。
(2)应用阿基米德原理计算浮力。
(3)应用图像欧姆定律及体积关系求浸没深度。
【解答】解:(1)放入物体M前,水的深度h1=12cm,根据图像可知当h1=12cm时,电阻R=60Ω,
则电流表示数为:I=;
(2)M漂浮在水中时浸入水中的深度为6cm,排开水的体积V排=SMh浸=200cm2×6cm=1200cm3,
根据阿基米德原理可得M漂浮在水中时所受到的浮力:
N/kg×1200×10﹣6m3=12N;
(3)当M放入水中漂浮时,水面上升的高度Δh==,
则M放入水中漂浮时,水箱中水的深度h2=h1+△h=12cm+4cm=16cm;
当电流为0.3A时,根据欧姆定律R=,由图像可知此时水的深度h3=18cm,
当电流表的示数为0.3A时,与M漂浮相比,水面上升的高度△h′=h3﹣h2=18cm﹣16cm=2cm,
因水面上升,所以物体M应下压,
根据ΔV排的两种计算方法可得:ΔV排=S容△h′=SM(△h′+h下压),
则物体M相对于漂浮在水中时向下移动的距离:
h下压===1cm。
答:(1)放入物体M前,电流表的示数为0.2A;
(2)M漂浮在水中时所受到的浮力为12N;
(3)当电流表的示数为0.3A时,物体M相对于漂浮在水中时移动的距离为1cm。
30.(1)未放入物体时,水对容器底的压强为900Pa;
(2)R2的阻值为10Ω:
(3)物体A的密度为0.6×103kg/m3。
【分析】(1)知道未放入物体时水的深度,利用p=ρgh求出水对容器底的压强;
(2)由电流先增大后减小可知,当GA=F浮时,杆子受到的力F=0,由图乙可知,此时R1=10Ω,由图甲可知,R1、R2串联,根据欧姆定律可知此时的电流最大,利用串联电路特点和欧姆定律求出R2的阻值;
(3)还未进入水中时,A的重力等于杆子的受到的力,此时I0=0.2A,根据欧姆定律和电阻串联的特点得出此时R1的阻值,由图乙可知,根据GA=F得出此时A的重力;
当I1=0.4A时,根据欧姆定律和电阻串联的特点得出此时R1的阻值,由图乙可知,此时杆子受到的力F1;
分此时杆给的力F1为向下或向上的拉力两种情况,对物体受力分析,结合阿基米德原理得出A的体积,进而得出物体和水的总体积,结合题意确定A的体积,利用密度公式得出物体A的密度。
【解答】解:(1)未放入物体时,水深为9cm,水对容器底的压强为:;
(2)由电流先增大后减小可知,当GA=F浮时,杆子受到的力F=0,由图乙可知,此时R1的阻值最小为10Ω,
由图甲可知,R1、R2串联,根据欧姆定律可知,此时电路中的电流最大:I2=0.5A,
由I=可知,R1、R2的总阻值:R===20Ω,
根据串联电路特点可知,R2的阻值:R2=R﹣R1=20Ω﹣10Ω=10Ω;
(3)还未进入水中时,A的重力等于杆子的受到的力,此时I0=0.2A,此时R1的阻值为,
由图乙可知,此时A的重力为GA=F=1.2N,
当I1=0.4A时,此时R1的阻值为,
由图乙可知,此时杆子受到的力为F1=0.2N,
若此时杆给的力F1为向下的拉力,则物体的重力和拉力之和等于浮力,即,
则A的体积为,
物体和水的总体积为,
依题意,
因为640cm3>600cm3,所以A的体积不为280cm3。
若此时杆给的力F1为向上的压力,则物体的重力等于压力与浮力之和,即,
则A的体积为,
物体和水的总体积为,
依题意,因为560cm3<600cm3,所以A的体积为,
物体A的密度为。
答:(1)未放入物体时,水对容器底的压强为900Pa;
(2)R2的阻值为10Ω:
(3)物体A的密度为0.6×103kg/m3。
31.(1)弹簧恰好处于自然状态,此时通过仪器A的电流为0.15A;
(2)若仪器A示数为0.2A时,物体排开水的体积V排为550cm3;
(3)仪器A示数为0.2A时,水槽中水的总质量为3125g。
【分析】(1)弹簧恰好处于自然状态,此时弹簧不受力,所以压杆没有压力,由乙图可知压力传感器的电阻,根据欧姆定律计算此时通过仪器A的电流;
(2)根据欧姆定律计算仪器A示数为0.2A时压力传感器的电阻,
由图可知此时压杆压力,根据杠杆平衡条件计算B处的拉力,根据重力公式计算物体的重力,根据称重法计算物体所受浮力,根据阿基米德原理计算物体排开水的体积;
(3)弹簧每受到1N的力时长度变化0.5cm,据此计算此时弹簧的伸长量,弹簧恰好处于自然状态时长度为10cm,弹簧每受到1N的力时长度变化0.5cm,物体的重力为6N,进一步计算挂上物体后的伸长量,据此计算加水后物体底面上升的高度,
由(2)得物体排开水的体积,根据体积公式计算物体浸入水的高度,根据体积公式计算水槽内水的体积,根据m=ρV计算水槽中水的总质量。
【解答】解:(1)弹簧恰好处于自然状态,此时弹簧不受力,所以压杆没有压力,由乙图可知压力传感器的电阻为40Ω,
由欧姆定律可得此时通过仪器A的电流为:I===0.15A;
(2)仪器A示数为0.2A时,压力传感器的电阻为:R1===30Ω,
由图可知,此时压杆压力为1N,根据杠杆平衡条件可知F×OA=F拉×OB,则F拉==1N×=0.5N,
物体的重力为:G=mg=0.6kg×10N/kg=6N,
所以物体所受浮力为F浮=G﹣F拉=6N﹣0.5N=5.5N,
物体排开水的体积为:V排===5.5×10﹣4m3=550cm3;
(3)弹簧每受到1N的力时长度变化0.5cm,所以此时弹簧的伸长量为Δl1=0.5N×0.5cm/N=0.25cm,
弹簧恰好处于自然状态时长度为10cm,弹簧每受到1N的力时长度变化0.5cm,物体的重力为6N,挂上物体后的伸长量为Δl2=6N×0.5cm/N=3cm,
所以加水后物体底面上升的高度为Δl=Δl2﹣Δl1=3cm﹣0.25cm=2.75cm,
由(2)得物体排开水的体积为550cm3,所以物体浸入水的高度为h1===5.5cm,
水槽内水的体积为:V=S(h+Δl)+(S﹣S正方体)h1=300cm2×(4cm+2.75cm)+(300cm2﹣10cm×10cm)×5.5cm=3125cm3,
水槽中水的总质量为:m=ρV=1g/cm3×3125cm3=3125g。
答:(1)弹簧恰好处于自然状态,此时通过仪器A的电流为0.15A;
(2)若仪器A示数为0.2A时,物体排开水的体积V排为550cm3;
(3)仪器A示数为0.2A时,水槽中水的总质量为3125g。
32.(1)汽车入水前电路中R1的电流为0.1A;
(2)汽车受到的重力2.5×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
【分析】(1)汽车入水前,R1表面受到水的压力为0,由图丙可知此时其阻值为20Ω,由乙图知R1和R2组成串联电路,电压表测的是R2两端的电压,示数为4V,已知总电压,根据串联电路的电压规律求出R1两端的电压,利用欧姆定律求出汽车入水前电路中的电流I;
(2)根据水池的水位比汽车入水前上升的高度,求出汽车排开水的体积,利用阿基米德原理求出汽车受到的浮力;
(3)先利用(1)中信息求出电阻R2的阻值,根据题中信息:汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于4V,即R1两端的电压为4V时,气囊充气打开,求出此时R2两端的电压,利用欧姆定律求出电路中的电流I′,利用欧姆定律求出电阻R1的阻值,由图丙可知,此时R1表面水的压力,即汽车底部A处受到水的压力,根据p=得出此时压敏电阻所受的压强,根据hA=得出气囊充气打开时汽车A处浸入水中的深度。
【解答】解:(1)汽车入水前,R1表面受到水的压力为0,由图丙可知此时其阻值为20Ω,由乙图知R1和R2组成串联电路,电压表测的是R2两端的电压,示数为4V,
根据串联电路的电压规律U=U1+U2得,R1两端的电压为:U1=U﹣U2=6V﹣4V=2V,
电路中的电流为:I===0.1A;
(2)当汽车漂浮时,水池的水位比汽车入水前上升了10cm,
则汽车排开水的体积为:V排=S水池Δh=25m2×10×10﹣2m=2.5m3,
汽车受到的浮力为:F浮=ρ水gV排=1.0×103kg/m3×10N/kg×2.5m3=2.5×104N,
汽车漂浮时,汽车受到的重力等于浮力,所以汽车受到的重力为2.5×104N;
(3)汽车入水前,电压表的示数为4V时,电阻R2的阻值为:R2===40Ω,
汽车入水前把R2的滑片调到合适位置不动,把汽车吊入水池中缓慢下沉,直到a、b间的电压等于4V即R1两端的电压为4V时,气囊充气打开,
此时R2两端的电压为:U2′=U﹣U1′=6V﹣4V=2V,
电路中的电流为:I′===0.05A,
电阻R1的阻值为:R1′===80Ω,
由图丙可知,此时R1表面受到水的压力为15N,即汽车底部A处受到水的压力为15N,
此时A处所受水的压强为p===104Pa,
汽车A处浸入水中的深度为hA===1m。
答:(1)汽车入水前电路中R1的电流为0.1A;
(2)汽车受到的重力2.5×104N;
(3)气囊充气打开时汽车A处浸入水中的深度为1m。
同课章节目录
